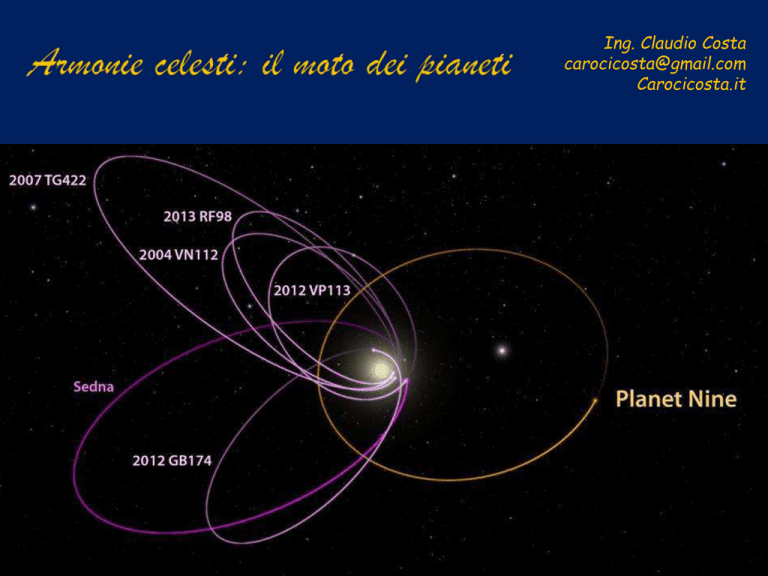
Ing. Claudio Costa
[email protected]
Carocicosta.it
«So che sono mortale, e la creatura di un giorno…
Ma quando scopro qualcosa nelle innumerevoli sfere rotolanti delle stelle,
I miei piedi non toccano più la terra: fianco a fianco con Zeus stesso,
bevo la mia coppa d’ambrosia, cibo degli dei…»
Claudio Tolomeo, Trattato Matematico, meglio noto come Almagesto
Oggi impariamo a scuola che il
sistema solare è un insieme di
corpi celesti mantenuti in orbita
attorno al Sole dalla forza di
gravità
È formato da otto pianeti, dai
rispettivi satelliti naturali, da
cinque pianeti nani e da miliardi
di corpi minori
Questi sono gli asteroidi, in gran
parte ripartiti fra due fasce (la
fascia principale e la fascia di
Kuiper, oltre l’orbita di Nettuno
fino a 50 UA), le comete, le
meteore e la polvere
interplanetaria
Il sistema solare è composto
inoltre dal disco diffuso e dalla
ipotetica nube di Oort (da 2.000
a 50.000 UA), sede di gran parte
delle comete
In ordine di distanza dal Sole,
gli otto pianeti sono:
Mercurio, Venere, Terra,
Marte, Giove, Saturno, Urano
e Nettuno
Attualmente cinque corpi del
sistema solare sono stati
classificati come pianeti nani:
Cerere, situato nella fascia
degli asteroidi, e altri quattro
corpi situati al di là
dell'orbita di Nettuno:
Plutone, Haumea, Makemake,
e Eris
Sei dei pianeti e tre dei
pianeti nani hanno in orbita
attorno a essi dei satelliti
naturali; inoltre tutti i pianeti
esterni sono circondati da
anelli planetari composti di
polvere e altre particelle
Ma procediamo storicamente…
L’obiettivo dell’astronomia fino al seicento è stato quello di dimostrare che i moti dei
pianeti erano regolari, nonostante l’apparente movimento alternato in avanti e all’indietro
rispetto alle stelle
Questo avrebbe permesso di prevedere la loro posizione in cielo
L’obiettivo fu stabilito da Platone nel IV
secolo A.C.
Platone assegnò ai suoi seguaci il
compito di mostrare che i moti planetari
erano altrettanto regolari di quelli degli
altri moti celesti, come le stelle
Il moto delle stelle è circolare e
uniforme, cosicché si doveva dimostrare
che anche quelli dei pianeti erano di
natura simile, o al massimo, formati da
combinazioni di moti circolari uniformi
Aristotele portò il
compito di Platone al
massimo
compimento:
seguendo Eudosso,
stabilì che i corpi
celesti si dovessero
muovere su 55 sfere
concentriche
Oltre la Terra per
lui vi erano, in
ordine, la Luna,
Mercurio, Venere, il
Sole, Marte, Giove,
Saturno, il cielo
delle stelle fisse e,
infine, il Primo
Mobile, che metteva
tutte le altre sfere
in movimento
Eudosso di Cnido (408 a.C. – 355 a.C.)
Tutti i video sulla pagina del Museo Galileiano:
http://catalogo.museogalileo.it/indice/IndiceVideo.html
Aristarco di Samo
(310 a.C. - 230 a.C.)
Aristarco, è noto soprattutto per
avere per primo introdotto una
teoria astronomica nella quale il
Sole e le stelle fisse sono immobili
mentre la Terra ruota attorno al
Sole percorrendo una circonferenza
L'unica opera pervenuta di
Aristarco è il breve trattato «Sulle
dimensioni e distanze del Sole e
della Luna» nel quale stima la
grandezza del Sole e della Luna e
calcola le relative distanze dalla
Terra
Aristarco stimò il rapporto tra le
distanze del Sole e della Luna come
compreso tra 18 e 20, mentre il
rapporto tra le distanze medie è in
realtà circa 400
Ipparco (Nicea 190 a.C. – 120 a.C.)
Fu il primo a sviluppare modelli accurati per
spiegare il moto del Sole e della Luna,
servendosi delle osservazioni e delle
conoscenze accumulate nei secoli dai popoli
della Mesopotamia, babilonesi per primi
Grazie alle sue teorie sui moti del sole e della
luna e alle sue conoscenze di trigonometria, è
stato probabilmente il primo a sviluppare un
metodo affidabile per la previsione delle
eclissi solari
Compilò un catalogo stellare e, probabilmente,
fu uno degli inventori dell'astrolabio
Fu proprio l'osservazione delle discordanze
tra il proprio catalogo e quello compilato da
Timocari e Aristillo nel 290 a.C. a fornirgli
l'indizio che lo condusse alla scoperta del
fenomeno della Precessione Degli Equinizi
Apollonio di Perga (262 a.C. – 190) a.C.)
Famoso per l’opera sulle sezioni coniche, gli è attribuita l’idea delle orbite eccentriche:
immaginando che i pianeti si muovessero su deferenti ed epicicli si poteva spiegare il moto
apparente dei pianeti, la velocità variabile della Luna e la variazione di luminosità degli
astri
Tutti questi movimenti
circolari portarono i Greci a
farsi un modello
«meccanico» del Cielo e
addirittura a realizzare
fisicamente una macchina
che li riproducesse
All’inizio del 1900 alcuni
pescatori trovarono nei
fondali dell'isola greca di
Antikythera un relitto resto
di un naufragio avvenuto nel
secondo quarto del I secolo
a.C., contenenti, insieme a
numerosi oggetti di quel
tempo, anche questo
meccanismo
La macchina è il più antico
calcolatore meccanico
conosciuto, databile intorno
al 150-100 a.C.
Si tratta di un sofisticato planetario, mosso come un orologio da ruote dentate, che serviva
per calcolare il sorgere del sole, le fasi lunari, i movimenti dei cinque pianeti allora
conosciuti, gli equinozi, i mesi, i giorni della settimana e le date dei giochi olimpici
Massimo Mogi Vicentini, ne ha ricostruito un modello
moderno perfettamente funzionante
Claudio Tolomeo
(100 circa – 175 circa)
Claudio Tolomeo fu astrologo, astronomo e
geografo di epoca imperiale e cultura
ellenistica che visse e lavorò ad
Alessandria d'Egitto
Considerato uno dei padri della geografia,
fu autore di importanti opere scientifiche,
la principale delle quali è il trattato
astronomico noto come Almagesto
Il titolo greco originale di quest'opera era
Mathematikè syntaxis ("Trattato
matematico")
Il nome "Almagesto" viene dall'arabo ed è
dovuto alla circostanza che, come per larga
parte della scienza e della filosofia greca
classica, la sua diffusione iniziale in Europa
è avvenuta soprattutto attraverso
manoscritti arabi che furono tradotti in
latino da Gerardo da Cremona nel XII
secolo
Saltando a piè pari tutto il
Medioevo (non dovremmo
visti i contributi dati
all’astronomia dagli Arabi…)
arriviamo a Niccolò
Copernico (1473-1543), nato
a Torun in Polonia e che
studiò all’Università di
Cracovia dove c’era una
tradizione importante in
astronomia, fra cui docenti
che non facevano mistero
della loro insoddisfazione
per la violazione del
principio del moto circolare
uniforme a opera degli
equanti tolemaici
Nella seconda metà del Cinquecento
si ebbe una rivoluzione
nell'atteggiamento degli astronomi
verso l'osservazione, determinata
dal danese Tycho Brahe (1546-1601)
Tycho era nobile di nascita : grazie a
questo, che lo sottraeva alle comuni
pressioni di carriera, poté vagare
liberamente da un'università
all'altra
Nel 1563, quando per la prima volta
in vent'anni Giove andò alla
congiunzione con Saturno mentre i
due pianeti si muovevano lentamente
contro lo sfondo delle stelle fisse, il
diciassettenne Tycho era già
abbastanza interessato
all'astronomia per fare semplici
osservazioni di questo fenomeno
Tycho trovò che la previsione della data di questo evento, calcolata sulla base delle
duecentesche Tavole Alfonsine (fondate sui modelli planetari tolemaici) era sbagliata di un
mese, mentre persino le moderne Tavole Pruteniche, fondate sui modelli di Copernico, davano
un errore di due giorni
Questo fatto lo convinse che l'astronomia doveva essere riformata su una base solida di
osservazioni accurate, e che tale precisione poteva venire solo da una combinazione di
miglioramento degli strumenti e di perfezionamento delle tecniche di osservazione
Nel novembre 1572, la natura
offrì all'umanità uno spettacolo
sorprendente
Un oggetto simile a un stella,
abbastanza luminoso da essere
visibile anche di giorno, apparve
nella costellazione di Cassiopea
Benché Tycho avesse solo
ventisei anni, e gli strumenti
astronomici a sua disposizione
fossero ancora modesti sia per
scala sia per qualità, egli riuscì
tuttavia a convincersi che
quell'oggetto fosse molto più in
alto della Luna, e fosse quindi un
corpo celeste
Oggi sappiamo che si trattava di
una Supernova, l’esplosione che
mette fine alla vita delle stelle
massicce: qui si vede il residuo di
gas in espansine della Nova di
Tycho
Tycho aveva così la prova che
si verificavano cambiamenti
anche in cielo
Si ripromise perciò che, se un
giorno fosse apparsa una
cometa, ne avrebbe misurato
con grande cura l'altezza per
verificare se fosse o no un
fenomeno terrestre
La natura si rivelò sensibile a
questo desiderio: nel 1577 si
presentò una cometa molto
luminosa, e le osservazioni di
Brahe ne rivelarono la natura
celeste
Il suo moto la portava infatti
ad attraversare le presunte
sfere invisibili che
trasportavano i pianeti nel loro
moto
Keplero non godette di nessuno dei
privilegi sociali di Brahe
Figlio di un padre attaccabrighe e di
una madre che, in seguito, riuscì solo
grazie a lui a evitare una condanna a
morte per stregoneria, nacque nel 1571
a Weil der Stadt, nei pressi di
Stoccarda
Se non fosse stato per il sistema
educativo del Ducato di Würtenberg,
che portava i giovani poveri, ma
meritevoli fino all’Università di
Tubinga, l’umanità avrebbe perso per
sempre un genio
Intendendo diventare pastore
luterano, cominciò a studiare alla
Facoltà delle Arti, dove apprese
l'astronomia
Il suo docente era Michael Màstlin
(1550-1631), un astronomo matematico
eccezionalmente ben preparato che
illustrò ai suoi studenti i meriti
dell'ipotesi copernicana
Copernico non aveva fatto letteralmente
nulla per promuovere la sua visione del
cosmo: le idee esposte nel I breve libro
cosmologico del De revolutionibus erano
oscurate dalla grande quantità di
matematica che dominava il resto del
volume
Non sorprende che alla fine del
Cinquecento i copernicani dichiarati
fossero rari
Del loro gruppo non faceva ancora parte
l'uomo che sarebbe diventato il più
efficace propagandista della nuova
visione del mondo: Galileo Galilei (15641642)
Isaac Newton nacque a
Woolsthorpe-by-Colsterworth nel
1642 e morì a Londra nel 1727
Fu filosofo, matematico, fisico e
alchimista: è considerato da molti
una delle più grandi menti di tutti i
tempi
4 Dicembre 2008
Universalmente noto soprattutto
per il suo contributo alla
meccanica classica, Isaac Newton
contribuì in maniera
fondamentale a più di una branca
del sapere
Pubblicò i “Philosophiae Naturalis
Principia Mathematica” nel 1687
nella quale descrisse la legge di
gravitazione universale e,
attraverso le sue leggi del moto,
creò i fondamenti per la
meccanica classica
Newton inoltre condivise con
Gottfried Wilhelm Leibniz la
paternità dello sviluppo del
calcolo differenziale
Gottfried Wilhelm Leibniz
4 Dicembre 2008
La tradizione vuole che Newton
fosse seduto sotto un albero di
mele quando una mela cadde sulla
sua testa e questo gli facesse
capire che la forza
gravitazionale terrestre e
celeste fossero la stessa cosa
In ogni modo si ritiene che anche
questa storia sia stata inventata
dallo stesso Newton più avanti
negli anni, per dimostrare quanto
fosse abile a trarre ispirazione
dagli eventi di tutti i giorni:
«Quando per la prima volta, la
nozione di forza di gravità si
formò nella mia mente. Fu
causato dalla caduta di una mela,
mentre sedevo in
contemplazione. Perché la mela
cade sempre perpendicolarmente
al terreno, pensai tra me e me,
non può cadere a lato o verso
l'alto, ma sempre verso il centro
della terra»
4 Dicembre 2008
Newton fu quindi il primo a dimostrare
che le stesse leggi della natura
governano il movimento della Terra e
degli altri corpi celesti
A Newton si deve anche la
sistematizzazione matematica delle leggi
di Keplero sul movimento dei pianeti
Egli generalizzò queste leggi intuendo
che le orbite (come quelle delle comete
potevano essere non solo ellittiche ma
anche iperboliche e paraboliche
4 Dicembre 2008
Una volta accettata la cornice
newtoniana, il programma era chiaro:
dimostrare matematicamente che tutti
i moti osservati dei corpi celesti erano
il risultato dell'attrazione
gravitazionale
Newton aveva mostrato, nei Principia,
che le comete obbedivano a regole e si
muovevano nel sistema solare su sezioni
coniche, anche se le loro orbite erano
molto diverse dalle ellissi quasi
circolari percorse dai pianeti
Le orbite delle comete erano così
allungate che in prossimità del Sole si
avvicinavano a una parabola
Se una cometa non arrivava al perielio il punto della sua orbita più vicino al
Sole - con una velocità abbastanza
elevata, non poteva, dopo averlo
aggirato, sottrarsi totalmente al suo
dominio perdendosi nello spazio
interstellare
Essa si allontanava invece
su un'orbita ellittica
destinata a riportarla un
giorno all'interno del
sistema planetario, anche
se su una traiettoria
modificata rispetto a quella
della visita precedente nel
caso che le fosse accaduto
di passare accanto a un
pianeta gigante
Nonostante tali modifiche,
però, l'orbita di una cometa
doveva conservare
caratteri simili in ogni
apparizione, e queste
apparizioni dovevano essere
separate nel tempo di
periodi simili
La documentazione storica
forniva qualche esempio in
proposito?
Edmund Halley intraprese la
ricerca necessaria, e trovò
rapidamente un primo esempio
possibile nella cometa del
1682: la sua orbita era
retrograda (ossia la cometa si
muoveva in senso opposto ai
pianeti), come quella delle
comete del 1531 e del 1607
Ulteriori ricerche mostrarono che tali orbite avevano in
comune vari altri caratteri, e nel 1695 Halley disse a
Newton di essere certo che si trattasse di riapparizioni
della stessa cometa
Nella sua previsione, Halley aveva tenuto conto
dell'accelerazione sperimentata dalla cometa a
opera dell'attrazione di Giove, quando si era
avvicinata a esso nel corso del suo passaggio
verso il Sole del 1682, ma non aveva preso in
considerazione le conseguenze opposte in
occasione della sua uscita dal sistema solare
Per rimediare a questo fatto si richiedevano
calcoli dettagliati e laboriosi, compito
affrontato nel giugno 1757 a Parigi da AlexisClaude Clairaut (1713-1765) e da due suoi
collaboratori
Essi analizzarono dapprima l'orbita della
cometa mentre usciva dal sistema solare dopo
l'incontro del 1531, e su questa base ne «ripredissero» il ritorno nel 1607, confrontando
poi la loro predizione con i dati storici
registrati
Poi analizzarono l'orbita della cometa in uscita
nel 1607, «predicendone» similmente il ritorno
del 1682
Imparando da questi quasi-esperimenti,
predissero in modo analogo il prossimo
ritorno: la cometa sarebbe passata
intorno al Sole alla metà dell'aprile 1759,
con un margine di incertezza di un mese
Fu una buona previsione
La cometa fu osservata per la prima
volta la notte di Natale del 1758 da un
astronomo dilettante nei dintorni di
Dresda, mentre il primo astronomo di
professione a osservarla fu il
cercatore di comete parigino Charles
Messier (1730-1817), quattro
settimane dopo
La cometa passò al perielio il 13 marzo
I parametri dell'orbita della cometa
furono molto simili a quelli delle
comete del 1531, 1607 e 1682: era
chiaro che erano altrettanti passaggi
della stessa cometa
La previsione di Halley si era
dimostrata corretta, e il
newtonianesimo aveva avuto il suo
massimo trionfo pubblico
Mentre stavano avendo luogo queste
dimostrazioni pubbliche molto seguite
dell'attrazione gravitazionale newtoniana,
un gruppo ristretto di grandi matematici
lavoravano a tavolino, esplorando le
conseguenze dell'attrazione fra il Sole, i
pianeti e i loro satelliti
Per realizzare questo programma
newtoniano arrivarono alla metà del
Settecento un gruppo straordinario di
talenti:
Jean le Rond d'Alembert (1717-1783), che
prese il nome dalla chiesa parigina sui cui
gradini era stato esposto neonato, e che in
seguito dedicò tutta la sua esistenza alla
matematica, vivendo a Parigi di una rendita
lasciatagli dal suo padre naturale
Lo svizzero Leonardo Eulero (1707- 1783),
che attratto a San Pietroburgo dalle
lusinghe di Caterina II la Grande, e poi a
Berlino da Federico II il Grande, tornò
infine nella città russa, dove morì
Il torinese Joseph-Louis Lagrange
(1736-1813), che fu convinto a
stabilirsi prima a Berlino e poi a Parigi
Gli ultimi decenni del Settecento e i primi
dell'Ottocento sarebbero stati dominati
da Pierre Simon de Laplace (1749-1827),
che sopravvisse alla Rivoluzione francese e
fu infine creato marchese
Alla metà del Settecento la «meccanica
celeste» fondata su princìpi newtoniani
aveva registrato molti successi
In particolare, le nuove tavole solari e
lunari tenevano conto delle perturbazioni,
ed erano molto più esatte delle tavole che
sostituivano
Rimanevano però due anomalie
sconcertanti: un'apparente accelerazione
di Giove e decelerazione di Saturno, note
dal tempo di Tycho Brahe, e un'apparente
accelerazione della Luna, che come aveva
mostrato Halley era in corso dall'Antichità
in poi
Queste tendenze avevano implicazioni
profonde: se fossero continuate
indefinitamente il sistema solare era
condannato a cambiare drasticamente, e
forse a perire
Eulero, Lagrange e Laplace
distinsero fra due tipi di
variazioni nei moti dei pianeti:
«periodiche» e «secolari»
Le variazioni periodiche erano
viste come oscillazioni in
longitudine, latitudine e
distanza dal corpo centrale, che
venivano corrette in tempi
relativamente brevi
Le variazioni secolari erano
invece mutamenti a lungo
termine: esse influivano sulla
forma e sull'orientamento
dell'orbita: sulla sua
eccentricità, sulla posizione
dell'asse dell'ellisse,
sull'inclinazione del piano
orbitale rispetto all'eclittica,
sulla posizione della linea dei
nodi (i punti in cui l'orbita
intersecava l'eclittica) e forse
anche sulla distanza media dal
Sole
Lagrange e Laplace
riuscirono invece a
dimostrare che tutte le
oscillazioni potevano essere
considerate periodiche e
dovute alle perturbazioni
reciproche dei pianeti
In altre parole il quadro del
sistema solare vedeva i cui
moti interni e i parametri
geometrici erano soggetti
solo a oscillazioni minori sui
loro valori medi
Laplace credeva in effetti di
avere dimostrato che il
sistema solare era un
sistema stabile, dotato di
un'autoregolazione simile
sotto questo aspetto a quella
della natura vivente
Laplace descrisse questo quadro di un sistema solare stabile in una brillante opera
divulgativa, L’Exposition du système du monde, che apparve nel 1796
Ma fece anche dell'altro: tentò di spiegare come tale sistema potesse avere avuto origine
Poteva esserci stata, ai primissimi inizi del sistema solare, una gigantesca nebulosa o un
vortice rotante intorno al Sole, e i pianeti e i loro satelliti potevano essersi condensati da
questa materia turbinante e dalle miriadi di particelle che si attraevano reciprocamente
Questa supposizione spiegava
come mai tutti i pianeti e i
satelliti allora noti orbitassero
intorno al Sole nella stessa
direzione, da ovest verso est, e
quasi nello stesso piano
Ammessa questa spiegazione, le
oscillazioni ben bilanciate nei
moti del sistema solare
sarebbero la conseguenza di
relazioni spaziali persistite dalle
origini caotiche del sistema
L'ipotesi che il vuoto contenesse (o avesse
contenuto) un pianeta «mancante» fu incoraggiata
da una relazione aritmetica che emerse nel
Settecento
Nell'opera Astronomiae physicae & geometricae
dementa del 1702, David Gregory (1659-1708)
notò che i raggi delle orbite planetarie erano
grosso modo proporzionali ai numeri 4, 7, 10, 15,
52, 95
Il divulgatore filosofico tedesco Christian Wolff
ripubblicò queste cifre in un'opera che pervenne
all'attenzione di Johann Daniel Tietz (più noto
come Titius, 1729-1796), professore di fisica
all'Università di Wittenberg
Nel 1766 lo stesso Titius tradusse in tedesco la
Contemplation de la nature del naturalista
francese Charles Bonnet, nel testo del quale
interpolò un paragrafo in cui, cambiando il 15 di
Gregory in 16 e il 95 in 100, presentò la sequenza
nella forma :
4, 4+3, 4+6, 4+12, 4+48 e 4+96
Nessuno dei pianeti noti corrispondeva al
termine mancante nella sequenza, 4+24
Nel 1772 una copia della seconda edizione
della traduzione tedesca capitò sotto gli
occhi del giovane astronomo Johann Elert
Bode (1747-1826), che stava dando gli ultimi
ritocchi a una nuova edizione della sua
fortunata introduzione all'astronomia
Bode fu affascinato dalla relazione e
concordò sulle osservazioni concernenti
l'inopportunità di quel vuoto:
«Si può credere che il Creatore dell'universo
abbia lasciato vuota questa posizione?
Certamente no!»
Bode si convinse che nello spazio
apparentemente vuoto fra Marte e Giove
dovesse celarsi un pianeta primario non
ancora scoperto, a circa 4 + 24 unità dal Sole
L'inclusione della relazione nel libro di Bode le
garantì una vasta pubblicità, e nel 1781 essa
ricevette un impulso sensazionale e del tutto
inatteso quando Wilhelm Herschel (17381822), organista nato a Hannover ma
trasferitosi nella stazione termale inglese di
Bath, divenne la prima persona nella storia a
scoprire un pianeta
Quando si imbatté in Urano non stava
cercando un pianeta; astronomo dilettante
autodidatta, non era neppure al corrente
dell'esistenza di congetture su pianeti
«mancanti»
Egli era interessato particolarmente alle
stelle, non al sistema solare, e a quell'epoca
stava usando un telescopio a riflessione che si
era costruito da sé per familiarizzarsi con le
stelle più luminose, che stava esaminando una
a una
Il 13 marzo 1781 la sua esplorazione sistematica del cielo lo condusse nella costellazione dei
Gemelli: qui si imbatté in un oggetto che astronomi di professione avevano poco prima
scambiato per una stella
Era, come notò nel suo diario, «un oggetto curioso, o una stella nebulosa o forse una cometa»
Se apparteneva al sistema solare, poteva darsi che si muovesse in modo percettibile contro
le stelle dello sfondo
Herschel tornò perciò sull'oggetto quattro giorni dopo, e vide che i suoi sospetti erano
giustificati, poiché l'oggetto si era mosso: poiché non era uno dei pianeti noti, suppose che
dovesse essere una cometa
Un amico che aveva conoscenze
scientifiche importanti informò
dell'avvistamento l'astronomo reale
Nevil Maskelyne e il professore di
astronomia a Oxford Thomas Hornsby
Pur osservando con strumenti di livello
professionale, nessuno dei due riuscì a
vedere alcun oggetto insolito in quella
regione del cielo, e trascorse un po' di
tempo prima che essi potessero
identificare la «cometa» di Herschel
Risultò che essa era invece un pianeta,
il primo scoperto dagli albori della
storia
Si trovò - sorprendentemente - che
l'orbita di Urano corrispondeva bene
al termine successivo nella sequenza
di Bode:
4 + 192 = 196
L'astronomo di corte a Gotha, il
barone Franz Xaver von Zach (17541832), divenne ora un convinto
assertore della relazione aritmetica, e
nel 1787 intraprese la ricerca di un
pianeta nel vuoto Marte-Giove, ma
senza successo
Il 21 settembre 1800 Zach si incontrò
con altri cinque astronomi a Lilienthal
Essi decisero di assicurarsi la
cooperazione dei principali astronomi
di tutt'Europa per formare un gruppo
di ventiquattro «poliziotti del cielo», a
ognuno dei quali sarebbe stata
assegnata una parte dello zodiaco, col
compito di mantenere una costante
vigilanza sugli estranei eventualmente
presenti nel suo distretto
I loro piani furono superati dagli eventi
Uno dei membri da cooptare doveva
essere il valtellinese Giuseppe Piazzi
(1746-1826), direttore
dell'Osservatorio di Palermo,
l'osservatorio europeo più a sud
Nel corso di un soggiorno a GreenwichLondra negli anni Ottanta, Piazzi aveva
convinto il famoso costruttore di
strumenti Jesse Ramsden a realizzare
per lui un superbo cerchio altazimutale
di un metro e mezzo di nuova
concezione, e non gli aveva dato requie
finché il lavoro non era stato portato a
termine
Alla svolta del secolo Piazzi era
impegnato a usare il cerchio verticale
per compilare un nuovo grande catalogo
stellare, di precisione superiore a quella
di tutti i cataloghi precedenti
Il 1 gennaio 1801 Piazzi, ancora all'oscuro del compito che stava per essergli assegnato
dagli astronomi di Lilienthal, era al lavoro come al solito sul suo catalogo
Misurò la posizione della stella zodiacale n. 87 del catalogo di Nicolas-Louis de Lacaille, e
colse l'opportunità di misurare una (presunta) stella di magnitudine 8 circa che la
precedeva
Il suo accurato metodo di lavoro comportava che egli rimisurasse le sue posizioni in una
notte successiva; e quando lo fece trovò che la «stella» di ottava grandezza sembrava
essersi mossa, movimento di cui egli poté trovare conferma le notti seguenti: non era
perciò una stella, bensì un corpo appartenente al sistema solare
Nell'intero mese di gennaio 1801 Piazzi continuò a osservare il nuovo oggetto del sistema
solare da lui scoperto ogni volta che le condizioni meteorologiche lo permettevano, e il 24
scrisse a Bode e ad altri annunciando la sua scoperta. Nella lettera a Bode parlò solo del
ritrovamento di una cometa, mentre in una all'amico Barnaba Oriani, dell'Osservatorio
milanese di Brera, confidò che:
«il non essere essa accompagnata da alcuna nebulosità e più il suo moto così lento e
uniforme, mi ha fatto più volte cadere nell'animo che forse possa essere qualche cosa di
meglio di una cometa»
Alla metà di febbraio l'oggetto era troppo vicino
al Sole per continuare a essere visibile, cosicché
Piazzi cominciò a investigarne l'orbita sulla base
delle ventiquattro osservazioni che era riuscito a
fare
Una malattia impedì a Piazzi di fare altri
progressi nell'analisi matematica delle sue
osservazioni, cosicché nel mese di aprile egli inviò
i suoi dati a Oriani a Milano, a Bode a Berlino e a
Lalande a Parigi, affidando in tal modo il problema
alla comunità astronomica europea
Per fortuna era emerso un brillante nuovo talento
matematico nella persona di Cari Friedrich Gauss
(1777-1855); entro novembre Gauss escogitò un
metodo che gli permise di calcolare le
caratteristiche dell'orbita
Sulla base di queste informazioni, Zach iniziò la
ricerca del pianeta perduto, che trovò l'ultima
notte dell'anno, esattamente nella posizione
predetta da Gauss
L'oggetto, chiamato da Piazzi Cerere, in onore
della dea protettrice della Sicilia, risultò trovarsi
press'a poco alla distanza predetta dalla «legge»
di Bode, e dapprima parve non ci fosse ragione di
dubitare del fatto che, come Urano, dovesse
essere un vero pianeta
Herschel trovò però, con grande sorpresa, di non
riuscire a scorgere il disco del pianeta, neppure
col suo grande telescopio
Pensò perciò che il pianeta dovesse essere ancora
più piccolo della Luna
Peggio ancora, in marzo H.W.M. Olbers trovò un
altro corpo mobile, che chiamò Pallade. Herschel
misurò anche il suo diametro, e pensò che dovesse
essere inferiore a 300 chilometri
Era chiaro che Pallade non era un pianeta
Come termine descrittivo di questa nuova specie
di corpo celeste, Herschel propose la parola
«asteroide»
Entro il 1891 furono scoperti
più di 300 asteroidi, e la
frequenza delle scoperte
aumentò di molto con l'uso
della fotografia
Max Wolf a Heidelberg
fotografò un grande campo
stellare con un'esposizione di
varie ore
Poiché il suo telescopio seguiva
esattamente la rotazione del
cielo, sulla fotografia le stelle
apparivano come immagini
puntiformi, mentre gli
asteroidi tradivano la loro
identità attraverso piccoli
tratti luminosi causati dalla
distanza percorsa durante
l'esposizione
Herschel aveva scoperto il pianeta Urano, e Piazzi il
pianetino Cerere, imbattendosi in essi in modo
inatteso mentre erano impegnati in studi sulle stelle
Poco dopo la scoperta di Urano nel 1781, Bode trovò
che la posizione del pianeta era già stata registrata
da Tobias Mayer nel 1756, e addirittura da John
Flamsteed nel 1690, che lo avevano scambiato
entrambi per una stella
Queste osservazioni aggiuntive permisero all'amico di
Bode Placidus Fixlmillner e ad altri di determinare i
parametri dell'orbita di Urano e di calcolare tavole
delle sue posizioni future
Ben presto il pianeta cominciò però a deviare
dall'orbita prevista
La situazione migliorò nel 1790, quando l'astronomo
matematico francese Jean- Baptiste-Joseph
Delambre (1749-1822) pubblicò tavole che
sembravano corrispondere abbastanza bene alle
osservazioni, ma fra il 1820 e il 1840 la teoria
dell'orbita di Urano riprese a discordare dalle
osservazioni
Nel 1845 i moti di Urano furono esaminati
da un astronomo che conosceva meglio di
ogni altro le tecniche della meccanica
newtoniana: Urbain-Jean- Joseph Le
Verrier (1811-1877), dell'Osservatorio di
Parigi
Egli presentò una prima comunicazione
sull'argomento all'Académie des Sciences
di Parigi nel novembre di quell'anno, e una
copia di essa pervenne ben presto
all'astronomo reale a Greenwich, George
Biddell Airy (1801-1892)
Nel giugno dell'anno seguente Le Verrier
presentò la seconda comunicazione, nella
quale fece l'ipotesi che il pianeta ignoto
occupasse il posto successivo nella
sequenza della «legge» di Bode,
concludendo infine che il pianeta, visto dal
Sole, doveva trovarsi allora a pochi gradi
dalla longitudine di 325°
All'insaputa di Le Verrier, stava lavorando
sullo stesso problema un giovane laureato di
Cambridge, John Couch Adams (1819-1892)
Anche lui aveva supposto che il pianeta
obbedisse alla «legge» di Bode, ed era
arrivato a una soluzione approssimata per la
posizione del pianeta nell'ottobre 1843
Distratto da compiti d'insegnamento, non
derivò un risultato più preciso fino al
settembre 1845, quando calcolò che la
longitudine eliocentrica del pianeta il 1
ottobre doveva essere di 323° 34‘
Fornito di una lettera di presentazione del
professore di astronomia a Cambridge James
Challis (1803-1882), Adams fece visita ad
Airy per presentargli la sua analisi, ma a
causa di una serie di incidenti non riuscì a
parlare con lui
Gli lasciò tuttavia un compendio dei suoi
risultati
L'arrivo, l'estate seguente, della
comunicazione di Le Verrier, con la sua
predizione quasi identica della longitudine
eliocentrica, stimolò Airy all'azione
A suo giudizio la ricerca di un pianeta non
ancora scoperto non era compito
dell'Osservatorio Reale, che era finanziato
con fondi pubblici, ma egli convinse Challis a
fare una ricerca a Cambridge, cosa che egli
fece
Purtroppo Challis non disponeva di carte
abbastanza precise di quella regione del cielo
L'unico modo in cui poteva identificare un
pianeta - un visitatore temporaneo di
quell'area - consisteva quindi nell'osservare
la regione in varie occasioni, per vedere se
nel frattempo qualcuna di quelle «stelle» si
fosse spostata
Fu un lavoro che Challis affrontò senza alcun
senso d'urgenza
Questo scarso impegno costò ad Adams la priorità
Nel frattempo Le Verrier aveva infatti convinto a
compiere una ricerca gli astronomi
dell'Osservatorio di Berlino, i quali disponevano di
una risorsa importante: il foglio del nuovo Atlante
stellare dell'Accademia di Berlino - non ancora
distribuito - della regione in oggetto
Pochi minuti dopo l'inizio della loro ricerca, il 23
settembre 1846, gli osservatori berlinesi,
capitanati da Johann Gottfried Galle, si
imbatterono in una «stella» che non era presente
sul foglio
Era il pianeta mancante
La scoperta di Nettuno, nel 1846, fu l'ultimo
trionfo della meccanica newtoniana: due astronomi
matematici, seduti a tavolino, erano risaliti col
calcolo dagli effetti - le deviazioni di Urano
dall'orbita predetta - alla causa, e avevano
predetto dove doveva trovarsi il colpevole, un
pianeta la cui esistenza nessuno aveva fino allora
mai sospettato

![4) SISTEMA SOLARE [Compatibility Mode]](http://s1.studylibit.com/store/data/001463874_1-3adbbbf9cb6e721746a78bbe6cecec0e-300x300.png)



![4) SISTEMA SOLARE [Compatibility Mode]](http://s1.studylibit.com/store/data/000853553_1-2fb4ff449974068ff3972659848e8322-300x300.png)