.CORSO di FISICA
Corso di Laurea per Infermieri
Università degli Studi di UDINE - Sede di Pordenone
Obiettivi
Costruire su concetti proposti e avvicinati nel pre-corso, una serie di
applicazioni nell’ambito medico propedeutiche allo sviluppo e alla comprensione di
temi di fisiologia e anatomia, oltre che di biologia.
Contenuti
ARGOMENTO
Lezione
Forze e baricentro; momenti e leve;
i posizionamenti, le posture e l’equilibrio; i sollevamenti.
Potenziale elettrico, potenziale di Nernst e bioelettricità.
I^
Fluidi: proprietà e dinamica dei fluidi. La circolazione sanguigna.
II^
I gas: le loro leggi e la respirazione.
Termodinamica e calore: temperatura, scambi di calore e
termoregolazione.
III^
Acustica: onde longitudinali; propagazione di energia con l’onda,
definizione di intensità sonora; lo stetoscopio; onde stazionarie;
scala della sensibilità sonora.
IV^
La natura della luce; ottica geometrica e propagazione della luce;
lenti, immagini, ingrandimenti e microscopio; le fibre ottiche e il
loro utilizzo nelle tecniche di indagine medica.
V^
Energia di legame, struttura del nucleo e elementi di radioattività;
tipologia delle emissioni radioattive, famiglie, interazione con i VI^ e VII^
tessuti fisiologici e con gli organi; pericolosità.
Energia di legame, struttura del nucleo e elementi di radioattività;
tipologia delle emissioni radioattive, famiglie, interazione con i
tessuti fisiologici e con gli organi; pericolosità.
VI^ e
VII^
Metodi
Lezioni dialogate attente a riprendere conoscenze introdotte nel precorso
e a sviluppare concettualità più elaborate e più mirate. Si utilizzeranno esercizi e
calcoli sviluppati dal docente per allargare la familiarità nei confronti degli
strumenti della disciplina.
Riferimenti
Il docente preparerà degli appunti che distribuirà lezione per lezione. Tali
appunti hanno come riferimento principale il testo:
A.H. CROMER “Fisica per Medicina, Farmacia e Scienze Biologiche, Piccin editore
PADOVA.
Il docente
________________________________________________________________________________
Corso di FISICA – Laurea per Infermieri
**pag. 1 di 14 **
[walter manzon]
________________________________________________________________________________
Corso di FISICA – Laurea per Infermieri
**pag. 2 di 14 **
Forze e baricentro; momenti e leve;
i posizionamenti, le posture e l’equilibrio; i sollevamenti.
Potenziale elettrico, potenziale di Nernst e bioelettricità.
1^ lezione
LE DOMANDE
- Che cos’è una forza e come si possono individuare le sue componenti?
- La definizione del baricentro; come si può individuare il baricentro in un
-
corpo esteso?
Come è possibile qualificare l’equilibrio di un corpo grazie al
posizionamento del corpo?
Che cos’è una leva?
Quanti sono i tipi di leva e che cosa li distingue ?
Che cosa si intende per potenziale elettrico ?
Come si crea la differenza di potenziale tra due soluzioni mantenute a
contatto ?
Che cos’è il potenziale d’azione e come si sviluppa un segnale elettrico lungo
un assone?
Vediamo due esempi di applicazioni di forza in ambito medico e fisiologico, dove è
opportuno pensare all’azione della forza in termini di componenti e cioè di parti
che agiscono autonomamente, obbedendo alle regole delle operazioni vettoriali.
La prima figura si riferisce ad una trazione imposta ad una gamba ferita, mentre
nella seconda si analizza il modo di agire del
bicipite corrispondentemente ad una posizione
assunta dal braccio.
Nel primo caso è opportuno specificare che la
presenza del filo e delle carrucole ha il compito
________________________________________________________________________________
Corso di FISICA – Laurea per Infermieri
**pag. 3 di 14 **
di determinare una modificazione della retta d’azione delle forze: le forze in
campo, in effetti sono due, entrambi di modulo: f1 f2 f 30N. corrispondenti al
peso che le determina ma dirette diversamente grazie all’azione della tensione del
filo: la prima dalla carrucola vicina al piede verso l’alto-destra, inclinata di
55o rispetto all’orizzontale; la seconda dalla medesima carrucola verso il bassodestra, inclinata di 25o rispetto all’orizzontale.
Seguiamo, comunque, nelle figure successive l’analisi delle componenti delle forze
in campo partendo dal primo caso.
Nella seconda figura la forza agente ( Fm , forza
muscolare) può essere pensata come scomposta
nelle componenti parallela all’avambraccio (forza
di stabilizzazione) che aiuta l’articolazione (il
gomito) a sostenere la postura dell’avambraccio
(“lo tiene agganciato”) e perpendicolare
all’avambraccio (forza di sostegno) che supporta il
peso dell’avambraccio alzato .
La
definizione
generale
di
BARICENTRO viene riportata nelle formule
che seguono: in esse va riconosciuta l’importanza delle masse del corpo: è agevole
individuare il baricentro nel caso di una struttura composita, mentre la
determinazione è molto più complessa
nel caso di un unico corpo che si
sviluppa
senza
interruzione
di
continuità nello spazio, quale ad
esempio il braccio riportato in figura,
dove si deve procedere, accettando
qualche approssimazione.
In questo caso, infatti, il corpo (il
braccio) può essere pensato come
sviluppato nell’unica dimensione, quella longitudinale il centro di massa (altra
denominazione del baricentro) si può collocare in corrispondenza del gomito, dove
è presente la freccia più lunga. Il baricentro può essere pensato anche come il
punto sul quale, se sostenuto per mezzo di un cuneo, si può sospendere il corpo
stesso e cioè il punto sul quale può essere pensata come concentrata tutta la
massa.
________________________________________________________________________________
Corso di FISICA – Laurea per Infermieri
**pag. 4 di 14 **
n
i xi
x1 x2 x3 ... xn
1
n
n
quest a formula è valida per sist emi di corpi con element i della st essa
xB
massa posizionat i in corrispondenza della posizione xi .
Nel caso in cui invece gli element i siano di massa diversa mi :
n
xB
m1 x1 m2 x2 m3 x3 ... mn xn
n
i mi
1
i
mi xi
1
n
i
mi
1
nel caso di piu' dimensioni valgono anche:
n
yB
i
mi yi
1
n
i
n
e zB
mi
1
i
mi zi
1
;
n
i
mi
1
con alla fine:
rB xB i yB j z B k
Un corpo è in equilibrio, e cioè non si sbilancia in avanti o in laterale,
quando la verticale del suo baricentro cade all’interno della superficie d’appoggio
(vedi figure con manichini).
Leve come macchine semplici: sono da considerare come macchine semplici tutti
quei dispositivi che siano in grado di intensità o direzione di una forza (anche una
semplice carrucola lo è); sono da considerare macchine complesse invece quei
dispositivi che hanno un motore in grado di sviluppare delle forze proprie.
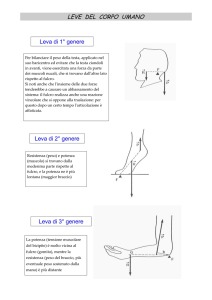
Oggetto principale della nostra
attenzione sono le leve che vengono
classificate come di I o , II o e III o genere, a
seconda di come sono disposti potenza (P)
e resistenza (R) rispetto al fulcro (F),
come visibile negli schemi presenti in
figura. La prima va considerata come la
forza attiva e la seconda come passiva.
Nella leva di I o genere il fulcro è
inserito tra potenza e resistenza : un
esempio di questo genere di leva può
essere l’altalena o anche il vecchio
martinetto.
Nella leva di II o genere il fulcro
invece si trova aldilà della resistenza
rispetto alla potenza: come buon esempio
si può ricordare la carriola.
________________________________________________________________________________
Corso di FISICA – Laurea per Infermieri
**pag. 5 di 14 **
Nella leva di III o genere il fulcro
si colloca aldilà della potenza rispetto
alla resistenza: un buon esempio di questo tipo di leva è costituito dal
sollevamento del peso nella mano da parte del bicipite come visibile nella figura a
fianco.
E’ evidente dalle figure schematiche sulle leve che, rispetto al fulcro, che
costituisce traccia di un ipotetico asse di rotazione, l’equilibrio in una leva viene
salvaguardato dalla compensazione dei momenti delle forze dovuti alla resistenza
e alla potenza, secondo la formula:
M R M P r R r P,
con r a rappresent are il vet t ore che collega il fulcro al punt o di azione della forza
La leva viene considerata conveniente o sconveniente a seconda del fatto
che lo potenza sia inferiore o superiore alla resistenza.
Si può ripensare anche alla definizione di baricentro di un corpo,
immaginandolo come l’ipotetico fulcro rispetto al quale tutti gli elementi del
corpo stesso sollecitano alla rotazione come tanti momenti, raggiungendo un
equilibrio globale.
Secondo una visione più ampia su forze e momenti, poi, è opportuno
consigliare l’assunzione di posizioni nei sollevamenti del tipo chiarito dalle figure
che seguono, dove vengono messe in evidenza anche scelte scorrette.
In entrambe i casi segnalati è chiarito che è conveniente sollevare o tenere
sollevato un peso il più possibile vicino al corpo in modo tale da minimizzare il
braccio della forza e quindi la potenza che serve ad equilibrare la resistenza
dovuta al peso dell’oggetto pesante. Infatti, guardando ad esempio il caso della
cassa, i muscoli della schiena che sopportano lo sforzo sono sollecitati ad
esprimere una forza (potenza) più grande quando il peso è più distante, agendo
essi a distanza fissa dalla posizione del fulcro, che in questo caso va collocato in
corrispondenza delle clavicole, circa.
________________________________________________________________________________
Corso di FISICA – Laurea per Infermieri
**pag. 6 di 14 **
Ripresa del potenziale elettrico.
Se due soluzioni globalmente neutre dal
punto di vista elettrico, contenenti ioni K e Cl
sono a concentrazione diversa, vengono poste a
contatto e mantenute separate da una membrana
permeabile solo agli ioni K , attraverso questa
avverrà una diffusione dalla più concentrata alla
meno concentrata e di svilupperà una differenza di
potenziale elettrico V tra le due, grazie alla
maggior presenza di ioni positivi nella soluzione
meno concentrata all’inizio. Tale differenza di
potenziale tenderà ad equilibrare con una propria
forza elettrica il disavanzo di concentrazione che
tende a far diffondere gli ioni potassio, portando il
sistema ad una situazione di equilibrio dinamico. La
differenza di potenziale che si instaura in tali
condizioni è detta potenziale di equilibrio di Nernst
ed è espressa dalla formula:
V V1 V2 2.3
c
kT
log 1 ;
e
c2
tale situazione si ritrova presente tra parte interna e
la parte esterna delle cellule e la membrana è
rappresentativa proprio della membrana cellulare; la
situazione all’interno del corpo umano prevede che alla
temperatura: T 37o C. (273 37) K . 310K . , con la costante:
k 1.38 x1023 J ./ K .
e
con
la
carica
dell’elettrone:
19
e 1.6 x10 C. , la formula diventi:
c
V V1 V2 (61.4 mV .) log 1
c2
e se si prende in considerazione il
caso particolare delle cellule nervose la
concentrazione di
nel fluido intracellulare vale
K
c1 0.141mol./ l. , mentre quella nel fluido extracellulare vale
c2 0.005mol./ l. e il valore che si determina, con questi valori per
il potenziale di equilibrio è:
0.141
V V1 V2 (61.4 mV .) log
61.4mV . 1.45 89.2mV .
0.005
La questione che ci interessa più da vicino è quella
relativa alla trasmissione lungo un assone che colleghi due
cellule nervose, come illustrato in figura: è il cosiddetto impulso
nervoso. All’interno dell’assone
le cellule prevedono una
differenza di potenziale simile a quella calcolata pari –85mV. .
________________________________________________________________________________
Corso di FISICA – Laurea per Infermieri
**pag. 7 di 14 **
La struttura di un assone può essere schematizzata grazie ad una forma
cilindrica come nella figura in pagina seguente; lungo tale cilindro si propaga
l’impulso che è a tutti gli effetti un segnale elettrico, ricostruibile attraverso lo
schema esplicativo che segue: quando l’assone viene stimolato in corrispondenza
del punto A, la sua membrana cellulare diventa temporaneamente permeabile
anche agli ioni Na , presenti anch’essi nei due fluidi intra- ed extra-cellulari, che
diffondono in un intervallo ampio t 0.2m sec. e neutralizzano la carica negativa
all’interno della cellula, inizialmente ricca di carica negativa, portando ad un
capovolgimento della differenza di potenziale, come
evidenziato nella figura rappresentativa del potenziale
d’azione, denominazione sotto la quale va questo tipo di
fenomeno.
Lo
sviluppo
dell’impulso del potenziale
d’azione
lungo
l’assone
avviene
poi
automaticamente grazie al
richiamo delle cariche di
segno opposto dalle zone
vicine.
Dopo il brevissimo
tempo di sviluppo di tale
potenziale viene invece a
ricadere immediatamente la
permeabilità
agli
ioni
sodio,
interrompendo
immediatamente la produzione del segnale.
________________________________________________________________________________
Corso di FISICA – Laurea per Infermieri
**pag. 8 di 14 **
Fluidi: proprietà e dinamica dei fluidi.
La circolazione sanguigna.
I1^ lezione
LE DOMANDE
- Che cos’è un fluido ?
-
-
-
-
+ Definizione
Quali sono le sue proprietà in condizioni statiche ?
+ Grandezze: pressione (sue unità di misura e processo di misura)
+ Legge di Pascal
+ Legge di Stevino
+ Spinta di Archimede
Che cos’è e di che cosa si occupa la dinamica dei fluidi ?
+ Definizione
Quali sono le grandezze fisiche da conoscere per poter caratterizzare il
fluido in movimento?
+ La portata Q
+ La viscosità
Quali sono le leggi che descrivono il moto di un fluido ?
+ Legge di Poiseuille
+ Teorema di Bernoulli
La circolazione sanguigna come caso particolare.
FLUIDO: è una sostanza (meglio, una fase di una sostanza) non rigida, che
quando viene sottoposta a forme che tendono a deformarla, non mantiene
una forma propria.
In questa lezione utilizzeremo il sostantivo fluido per trattare delle
caratteristiche dei soli liquidi, anche se tale parola riassume in se anche i gas
(vapori). Liquidi e gas (vapori) hanno comportamenti che li distinguono: il liquido
ha volume definito che mantiene, ma forma che si adatta al contenitore; il gas
(vapore) invece ha volume e forma adattabili.
La pressione è definita come forza che agisce su una superficie, secondo la
f
1Newton 1N .
p ; sua unit à di misura è: 1 Pascal
formula:
S
1m.2
1m.2
Le unità di misura per esprimere la pressione sono però molteplici: la più
importante ai nostri fini è il: mm.HG (il millimetro di mercurio); sono però
correntemente utilizzate anche l’ atm. (l’atmosfera) e il Bar (e da questo il mbar.,
millibar): le modalità di conversione sono le seguenti:
1atm. 1.013x105 Pa. 760mm.HG 1.013Bar 1013mBar.
________________________________________________________________________________
Corso di FISICA – Laurea per Infermieri
**pag. 9 di 14 **
La ragione della denominazione e del fattore di conversione che sussiste tra
atmosfera e millimetro di mercurio va fatta risalire a Torricelli, che con un noto
esperimento dimostrò che la pressione atmosferica è equivalente alla pressione
esercitata da una colonna di mercurio alta 760mm. .
Tale unità di misura è particolarmente significativa
in quanto tutte le valutazioni di pressione all’interno del
nostro organismo vengono espresse con essa: quando si
dice che una persona ha una pressione massima pari a 130,
si intende proprio che la pressione relativa interna arriva a
130mm.HG .
L’aggettivo relativa ha un’importanza fondamentale:
esso sancisce che quando si fanno valutazioni interne
all’organismo, ci si rifà ad una scala specifica: infatti se,
paradosso, la pressione interna fosse solo 130mm.HG , nel
momento in cui ci si procura una ferita, la dominanza
della pressione atmosferica ( 760mm.HG ) produrrebbe una
penetrazione del fluido aria all’interno delle vene/arterie;
in realtà ciò non si osserva. Anzi si spera che la ferita non
coinvolga grosse vene/arterie perché altrimenti il sangue
esce in maniera copiosa, segno della sua maggior pressione
interna. Dunque la pressione che si considera all’interno è
data dalla relazione:
pRELATIVA pINTERNA pATMOSFERICA
Al misura della pressione avviene
(o meglio avveniva) attraverso degli
strumenti detti manometri, i quali
provvedono a determinare la pressione
in un certo contenitore grazie ad una
pressione esercitata da una colonna di mercurio che equilibra
la spinta della pressione da misurare; si osservi in figura
l’utilizzo di un manometro che si
utilizzava qualche tempo fa e sotto un
equivalente strumento denominato sfigmomanometro.
Legge di PASCAL: “ In assenza di gravità un fluido in quiete
esercita la medesima pressione in tutte le direzioni”
Legge di STEVINO: “ La pressione esercitata da un fluido ad una
certa profondità è proporzionale alla profondità
stessa e alla sua densità”
________________________________________________________________________________
Corso di FISICA – Laurea per Infermieri
**pag. 10 di 14 **
p po d g h
d : densit à del liquido
h : profondit à
Principio dI ARCHIMEDE: “Un corpo immerso in un liquido riceve una spinta dal basso
verso l’alto pari al peso del liquido spostato”
Infatti considerata corretta la legge di Stevino, si può considerare che un
oggetto sia spinto maggiormente alla profondità della sua base inferiore (fate
riferimento al cilindro in figura) piuttosto che alla profondità della sua base
superiore: da ciò uno sbilanciamento verso l’alto della spinta, che a livello di
grandezza è una forza.
p dg (h h) dgh d g h
con d densit à del liquido; ma:
f verticale p A d g h A,
con A superficie della sezione del cilindro;
f verticale d h A g d Vol g m g
che rappresent a il peso del volumet t o del liquido corrispondent e al cilindro.
In particolare, dalla legge di Stevino, si può dedurre che la pressione
esercitata non dipende dalla superficie sulla quale viene esercitata, dato che nella
sua espressione non è direttamente coinvolto alcuna termine di superficie.
DINAMICA DEI FLUIDI: si occupa di definire le proprietà nel movimento dei
fluidi, considerandone anche la cause.
IPOTESI CHE PER NOI VALE PER TUTTA LA DINAMICA:
il fluido è incomprimibile e cioè non può essere né schiacciato, né fatto
espandere; mantiene sempre il suo volume.
La prima grandezza da valutare nel considerare il movimento di un fluido
(liquido in questo caso) è la portata, che si definisce come quantità di volume
trasportata in un condotto per unità di tempo, secondo la:
Vol ( A x)
x
Q
A
A v
t
t
t
Qmassa d Q d A v
Q da misurare in m.3 / sec. e Qmassa in kg./ sec.
Il trasporto di liquido (nella direzione orizzontale) è causato da una
differenza di spinta lungo il tubo, il condotto attraverso il quale avviene; si può
ottenere dunque grazie ad una differenza di pressione tra sezione iniziale del
tubo e sezione finale, secondo la legge di Poiseuille:
________________________________________________________________________________
Corso di FISICA – Laurea per Infermieri
**pag. 11 di 14 **
Q
R 4 p1 p2 p1 p2
8 l
, con: R
8 l
R
R4
R rappresent a il raggio del condot t o
l la sua lunghezza
p1 p2 la differenza di pressione
la viscosit à del liquido
In tale relazione appare una grandezza nuova ed è la viscosità : essa
rappresenta la forma d’attrito che condiziona il moto di un liquido all’interno di
una conduttura. Dalla relazione:
f
d
Av
f vis cos a
o vis cos a
d
Av
A sezione della condut t ura
dove:
v velocit à di uno st rat o diliquido
d dist anza t ra due st rat i successivi di liquido
Si può introdurre tale grandezza particolare: la formula mostra che
l’esistenza della forza viscosa (di attrito interno al liquido) è dovuta alla difficoltà
di scorrimento di uno strato di liquido rispetto ad uno strato immediatamente
vicino (si può parlare anche di gusci concentrici, all’interno di un tubo): tale
difficoltà è direttamente proporzionale alla velocità del liquido nella conduttura,
all’area della stessa e inversamente proporzionale alla distanza tra strati
considerati: la costante di proporzionalità che regola queste proporzionalità è
proprio la viscosità (sua unità di misura nel Sistema
Internazionale è Pa. sec. ).
La grandezza che viene definita in coda alla
legge di Poiseuille introduce la resistenza R e si vede che
all’aumentare di tale resistenza, a parità di differenza
di pressione, diminuisce la portata: si noti che essa
aumenta con la viscosità e diminuisce con la quarta
potenza del raggio della conduttura. Tale grandezza rende conto della perdita di
pressione cui è soggetto il moto del fluido: provate infatti a annaffiare un prato
con un tubo di gomma agganciato ad un rubinetto, ma molto lungo: noterete
sicuramente una bella differenza di pressione dell’acqua in uscita rispetto alla
pressione di uscita dal rubinetto!
In appendice sono riportati i valori di caduta di pressione del sangue
nell’attraversamento di un capillare, di calcolo di portata media dell’aorta e infine
di resistenza media su tutto il sistema circolatorio (vedi appendice).
Nello schema sottostante vengono riportati alcuni valori di viscosità per
fluidi noti:
Plasma sanguigno
Sangue intero
Temperatura (°C)
Densità (kg./m3)
Viscosità (Pa. x sec.)
37
37
1030
1050
0.0015
0.004
________________________________________________________________________________
Corso di FISICA – Laurea per Infermieri
**pag. 12 di 14 **
Glicerina
Mercurio
Olio per macchina
Acqua
Aria
Elio
20
20
38
4
37
0
40
20
1260
13600
1000
996
1.30
1,16
0.178
1,49
0.00155
0.034
0.00179
0.000691
0.0000171
0.0000190
0.0000125
Lo scorrimento del liquido all’interno del condotto
avviene, alla luce dell’ipotesi di incomprimibilità del
liquido, in modo tale che se si passa , a parità di portata,
da una sezione più ampia ad una sezione più limitata (e
cioè diminuisce il raggio della conduttura), la velocità del
liquido è destinata ad aumentare ( Q v A cost ant e ),
mentre la pressione a diminuire; la motivazione di ciò va
ricavata nella legge di Bernoulli, che solamente citiamo:
1
p d g h d v 2 cost ant e
2
Passiamo finalmente a considerare la circolazione
del sangue, facendo riferimento allo schema riportato: dal
grafico qui a fianco si può notare come la pressione del
sangue, nel fluire all’interno del sistema circolatorio, sia
destinata a calare man mano che si va dal ventricolo
sinistro all’atrio destro e cioè man mano che si percorre tutto il circuito interno;
la caduta di pressione va letta proprio alla luce della resistenza offerta dai vasi
sanguigni al passaggio del plasma; il cuore, con la sua potenza (circa 1 Watt),
provvede al sostentamento di tutto il sistema cardio-circolatorio.
Anche il rimpicciolimento dei vasi e la variazione di altezza nel
posizionamento dei vasi sanguigni ha un ruolo nella modificazione del valore della
pressione; la caduta più ripida del valore della pressione (da 80 a 25 mm.HG ca.) si
ha in corrispondenza del passaggio dalle arterie ai capillari e, in particolare, nel
passaggio nelle arteriose, dove la caduta di pressione è sostanziale (55 mm.HG ca.)
principalmente a causa della diminuzione delle dimensioni della loro sezione.
APPENDICE
________________________________________________________________________________
Corso di FISICA – Laurea per Infermieri
**pag. 13 di 14 **
CADUTA DI PRESSIONE DEL SANGUE NELL'ATTRAVERSAMENTO DI UN CAPILLARE
l 1mm. ca è la lunghezza t ipica di un capillare
R 2 m. è il suo raggio t ipico
4 x10-3 Pa. sec. è la sua viscosit à
La cadut a di pressione divent a:
-3
3
15
3
8l Q 8 4 x10 Pa. sec. 10 m. 4 x10 m. / sec.
p p1 - p2
2.5 x103 Pa. 18.75mm.HG
4
4
6
R
2 x10 m.
CALCOLO DELLA PORTATA MEDIA DEL SANGUE PER LE AORTE
Q v A, con v velocit à media del flusso sanguigno e A sezione media dell'aort a
essendo : v 0.33m./ sec. e A R 2 (0.9 x102 m.) 2 2.5 x104 m.2
per la port at a all'int erno delle aort e sarà:
Q v A 0.33m./ sec. 2.5 x104 m.2 0.83x104 m.3 / sec. 83 x10 6 m.3 / sec. 83cm.3 / sec.
CALCOLO DELLA RESISTENZA MEDIA NEL SISTEMA CIRCOLATORIO
In un adult o normale, la port at a del sangue è: Q 0.83x104 m.3 / sec.
Lo sbalzo globale di pressione è: p p1 p2 90mm.HG 1.2 x104 Pa.;
per la resist enza R sarà:
R
p1 p2
1.2 x104 Pa.
1.44 x108 Pa. sec.
4
3
Q
0.83x10 m. / sec.
________________________________________________________________________________
Corso di FISICA – Laurea per Infermieri
**pag. 14 di 14 **