SESTA LEZIONE-teoria delle parallele
Riprendiamo la discussione del teorema degli angoli alterni interni.
Questo teorema è alla base della teoria delle parallele. Da esso discendono i criteri di parallelismo.
Due rette a e b e una secante comune c definiscono gli angoli alterni interni 1 e 2.
Dall'uguaglianza o meno di questi due angoli vogliamo dedurre il parallelismo delle rette a e b.
Il teorema si divide in due parti (che sono le Proposizioni 26 e 27 di Euclide, l'una inversa dell'altra):
Parte 1: se 1=2 allora a // b
(l'uguaglianza degli angoli indica il parallelismo delle rette)
Si ragiona per assurdo, negando la validità della tesi; si dimostra che si arriva ad una contraddizione.
Se a non fosse parallela a b, le due rette si intersecherebbero in un punto, diciamo a destra della secante ,
formando con essa un triangolo. Devo immaginare la figura seguente
In questa situazione 1 è diventato angolo esterno al triangolo ABC; dunque per il teorema dell'angolo
esterno sarebbe maggiore di ogni angolo interno non adiacente.
Perciò se ne dovrebbe concludere che: 1>2.
Quindi negare la tesi porta ad una condizione contraria all'ipotesi.
Valendo l'ipotesi 1=2, non si può negare la tesi e quindi bisogna ammettere che a // b.
Parte 2: se a // b allora 1=2 (il parallelismo di a e b implica l'uguaglianza degli angoli alterni interni formati
da una qualsiasi secante comune).
Questo è un punto cruciale nello sviluppo della geometria di Euclide: per la prima volta Euclide usa il
postulato delle parallele (o quinto postulato).
Ricordiamo che il postulato riguarda gli "angoli coniugati" formati da una qualsiasi secante c delle rette a e
b.
Afferma che se la somma degli angoli 2 e 3 è minore di due angoli retti, le rette a e b necessariamente si
intersecano (e quindi non possono essere parallele) dalla parte della coppia di angoli coniugati che
soddisfano la diseguaglianza predetta.
(si può fare vedere che questo postulato è equivalente all'affermazione che per un punto A non
appartenente alla retta a passa una ed una sola parallela ad a).
Ancora una volta si ragiona per assurdo:
Supponiamo che 1>2:
introduco l'angolo 3 adiacente ad 1 rispetto all'obliqua c di a.
Per il teorema degli angoli adiacenti:
1 + 3 = 2 retti.
Di conseguenza la diseguaglianza ammessa 2<1 implica
2 + 3 < 1 + 3 = 2 retti
Quindi la secante c forma con le rette a e b angoli coniugati che sommano meno di due retti: per il quinto
postulato queste due rette devono intersecarsi. Ciò è in contraddizione con l'ipotesi che a sia parallela a b.
La negazione della tesi è incompatibile con l'ipotesi. La tesi è perciò vera: gli angoli 1 e 2 sono
necessariamente uguali.
se a // b
allora 1 = 2
Un semplice corollario riguarda gli angoli corrispondenti e gli angoli coniugati:
1 e 2 : alterni interni
4 e 2: corrispondenti
2 e 3: coniugati
Da 1=2 (alterni interni) segue che 4=2 (uguaglianza degli angoli corrispondenti) e che 2+3=2 retti (gli angoli
coniugati si comportano come angoli adiacenti).
Spiegazione:
perché 4 e 1 sono opposti al vertice e 1 e 2 sono alterni interni
2 + 3 = 4 + 3 = 2 retti
perché 4 e 3 sono adiacenti
Le tre condizioni (fra loro equivalenti):
1. gli angoli alterni interni sono uguali
2. gli angoli corrispondenti sono uguali
3. gli angoli coniugati hanno somma pari a due angoli retti
costituiscono i criteri di parallelismo (Proposizione 28 di Euclide).
Punto 5: Applicazioni ai triangoli
Dai due risultati precedenti Euclide deduce una catena di notevoli proprietà soddisfatte dai lati e dagli
angoli di un qualsiasi triangolo.
Enunciamo le tre proprietà che sono una diretta conseguenza del teorema dell'angolo esterno e che hanno
quindi la forma di diseguaglianze (le possiamo chiamare diseguaglianze triangolari sugli angoli e sui lati di
un triangolo).
Proposizione 17 (diseguaglianza sugli angoli): in ogni triangolo la somma di due angoli interni è minore di
due retti.
Proposizioni 18 e 19 (diseguaglianza lato-angolo): in ogni triangolo a lato maggiore si oppone l'angolo
maggiore e viceversa.
Proposizione 20 (diseguaglianza triangolare sui lati): in ogni triangolo la somma di una coppia di lati è
maggiore del terzo lato.
Se utilizziamo il teorema degli angoli interni possiamo essere più precisi sulla somma degli angoli interni
ad un triangolo:
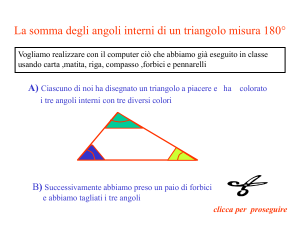
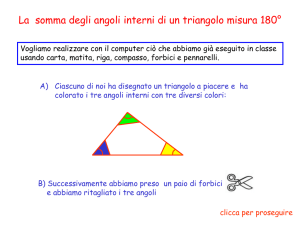
Proposizione 32: in ogni triangolo la somma dei tre angoli interni è pari a due angoli retti.
Spiegazione:
per sommare gli angoli interni penso di trasportare gli angoli 1 e 2 da A e B in C.
Per questo uso la tecnica delle parallele che mi assicura che gli angoli alterni interni e gli angoli
corrispondenti sono uguali (le parallele forniscono un metodo di trasporto degli angoli).
Prolungo la base BC nella retta BD; poi mando da C la parallela CE al lato BA.
Considero l'angolo 2 ‘ alterno interno di 2 e l’angolo 1‘ corrispondente di 1:
per i criteri di parallelismo abbiamo che
e
. Perciò :
perché adiacenti.
(La filosofia della dimostrazione è importante : per sommare o confrontare cose distanti si applica il
trasporto per parallelismo).
Esempio di geometria non euclidea: nel triangolo equilatero sulla sfera i cui lati sono un meridiano che dal
polo scende fino all’equatore, un arco di 90° di equatore e il secondo meridiano che dall’equatore ci riporta
al polo la somma degli angoli interni è 270°. Questo esempio mostra che la somma degli angoli interni ad
un triangolo sferico è diversa da 180°. Ciò è possibile perché sulla sfera non vale il postulato delle parallele.
Punto 6: Applicazioni ai parallelogrammi.
Abbiamo visto l'importanza delle parallele per trasportare e quindi confrontare angoli e segmenti. Da qui
segue che il parallelogramma diventa uno strumento essenziale nella geometria di Euclide (così
fondamentale da essere lo strumento base nella dimostrazione dei teoremi di Pitagora e Talete).
Usando i risultati noti, Euclide dimostra rapidamente la seguente proposizione, che semplicemente
enunciamo:
Proposizione: in ogni parallelogramma i lati opposti sono uguali e paralleli, gli angoli opposti sono uguali e
le diagonali si bisecano.
La nostra attenzione è ora rivolta ad un'altra proprietà dei parallelogrammi: l'uguaglianza in estensione,
distinta dall'uguaglianza in forma. Esistono figure di forma diversa che hanno la stessa estensione in
quanto composte dalle medesime parti montate in maniera diversa. Ad esempio