APPUNTI DI GEOMETRIA NELLO SPAZIO
CLASSE 5^C s
ALCUNI POSTULATI DELLO SPAZIO :
1. Per tre punti non allineati passa uno e un solo piano.
2. Fissati due punti in un piano, la retta passante per i due punti giace interamente sul piano.
3. Un qualunque piano divide l’insieme dei punti dello spazio che non gli appartengono in due regioni
tali che :
due punti qualsiasi della stessa regione sono estremi di un segmento che non interseca il
piano;
due punti qualsiasi di regioni diverse sono estremi di un segmento che interseca il piano.
RETTE E PIANI NELLO SPAZIO
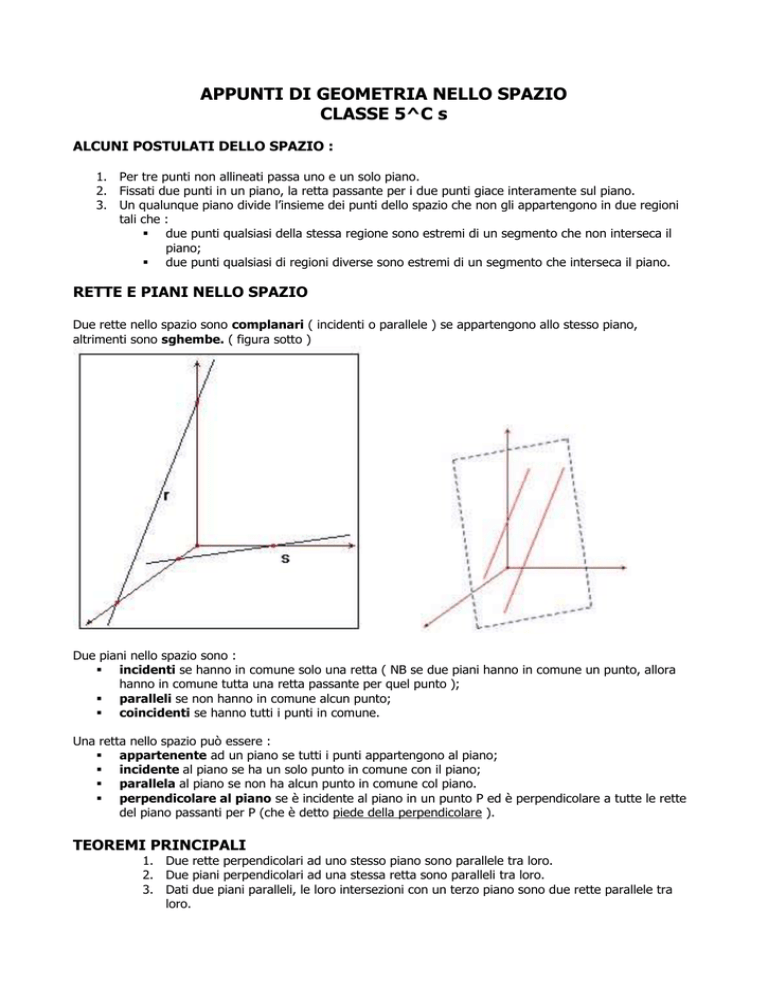
Due rette nello spazio sono complanari ( incidenti o parallele ) se appartengono allo stesso piano,
altrimenti sono sghembe. ( figura sotto )
Due piani nello spazio sono :
incidenti se hanno in comune solo una retta ( NB se due piani hanno in comune un punto, allora
hanno in comune tutta una retta passante per quel punto );
paralleli se non hanno in comune alcun punto;
coincidenti se hanno tutti i punti in comune.
Una retta nello spazio può essere :
appartenente ad un piano se tutti i punti appartengono al piano;
incidente al piano se ha un solo punto in comune con il piano;
parallela al piano se non ha alcun punto in comune col piano.
perpendicolare al piano se è incidente al piano in un punto P ed è perpendicolare a tutte le rette
del piano passanti per P (che è detto piede della perpendicolare ).
TEOREMI PRINCIPALI
1. Due rette perpendicolari ad uno stesso piano sono parallele tra loro.
2. Due piani perpendicolari ad una stessa retta sono paralleli tra loro.
3. Dati due piani paralleli, le loro intersezioni con un terzo piano sono due rette parallele tra
loro.
4. Teorema delle tre perpendicolari : Se dal piede delle perpendicolare ad un piano si
traccia la perpendicolare ad una qualunque retta nel piano, quest’ultima risulta
perpendicolare al piano individuato dalle prime due.
5. Teorema di Talete nello spazio : Un fascio di piani paralleli intersecati da due trasversali
intercetta su di esse segmenti corrispondenti proporzionali.
6. Se una retta passante per un punto esterno ad un piano è parallela ad una retta del piano,
essa è parallela al piano.
7. Se per una retta parallela ad un piano si conduce un piano incidente al primo, la retta
intersezione tra i due piani è parallela alla retta data.
Si dice distanza tra due piani paralleli la lunghezza del segmento intercettato dai due piani su una
qualunque retta perpendicolare ai due piani.
Si dice distanza di un punto da un piano la lunghezza del segmento che ha per estremi il punto stesso e
il piede della perpendicolare al piano passante per P ( NB Dato un punto P ed un piano α esiste ed è unica la
retta perpendicolare al piano passante per P )
ANGOLO RETTA- PIANO
Si dice proiezione di un punto su un piano il piede della perpendicolare condotta dal punto al piano.
Si dice proiezione di una figura su un piano la figura costituita dalle proiezioni sopra il piano dei punti della
figura data.
NB : La proiezione di una retta su un piano non perpendicolare ad essa è una retta.
Si dice angolo di una retta con un piano l’angolo acuto che la retta forma con la sua proiezione sopra il
piano.
ANGOLI DIEDRI
Dati nello spazio due semipiani aventi la stessa retta origine, si definisce diedro ognuna delle due parti (
compresi i semipiani ) in cui essi dividono lo spazio. La retta origine dei semipiani si dice spigolo del diedro
e i semipiani si chiamano facce del diedro.
Si dice sezione normale di un diedro l’angolo che si ottiene come intersezione tra il diedro ed un
qualunque piano perpendicolare al suo spigolo.
NB tutte le sezioni normali di un diedro sono congruenti in quanto tutte le sezioni parallele tra loro , anche
quelle non normali, sono congruenti tra loro.
Si dice ampiezza di un diedro l’ampiezza della sua sezione normale. Un diedro si dice retto, acuto o
ottuso a seconda che la sua sezione normale sia un angolo retto, acuto o ottuso.
Due piani incidenti si dicono perpendicolari quando dividono lo spazio in quattro diedri congruenti ( tutti
retti).
ANGOLOIDI
Date nello spazio n semirette distinte aventi la medesima origine e tali che, considerate in un certo ordine,
ciascun piano individuato da due semirette consecutive lasci da una stessa parte le rimanenti, si definisce
superficie piramidale la figura formata dagli angoli individuate dalle coppie di semirette consecutive.
L’origine comune delle semirette si chiama vertice della superficie; le semirette si dicono spigoli e gli angoli
facce.
La figura solida formata da una superficie piramidale e da tutti i suoi punti interni è detta angoloide.
Un angoloide si dice triedro, tetraedro, pentaedro,…secondo che abbia 3, 4, 5 facce.
NB
1. Ogni faccia di un poliedro è minore della somma delle altre e la somma delle facce di un angoloide è
minore di quattro angoli retti.
2. Ogni faccia di un triedro è minore della somma delle altre due e maggiore della loro differenza.
3. Le sezioni parallele di un angoloide sono poligoni simili in cui i perimetri sono proporzionali alle
distanze del vertice dai piani delle sezioni.
POLIEDRI
Un poliedro è una figura solida limitata da un numero finito di poligoni appartenenti a piani diversi e tali che
il piano di ogni poligono non attraversi il solido.
PRISMA
Un prisma è un poliedro delimitato da due basi che sono poligoni congruenti posti su piani paralleli e da
facce laterali che sono parallelogrammi. La distanza fra i piani contenenti le basi è l’altezza del prisma; le
diagonali sono segmenti che congiungono due vertici non appartenenti alla stessa faccia.
Un prisma è retto se gli spigoli laterali sono perpendicolari ai piani delle basi, è regolare quando è retto e
le sue basi sono poligoni regolari.
Un prisma è un parallelepipedo se anche le sue basi sono parallelogrammi.
Una piramide è la parte di angoloide compresa tra il suo vertice e un piano che interseca tutti i suoi spigoli.
La piramide è dunque un poliedro delimitato da un poligono detto base e da facce laterali triangolari
che hanno in comune tutte un vertice, detto vertice della piramide, e hanno il lato opposto a tale vertice
coincidente con un lato del poligono di base. La distanza tra il vertice della piramide e il piano della base è
detta altezza della piramide.
Una piramide è retta quando nella sua base si può inscrivere una circonferenza il cui centro è la proiezione
ortogonale del vertice della piramide sul piano di base. In questo caso le altezze delle facce laterali passano
per i punti di tangenza dei lati di base con la circonferenza e sono tutte congruenti . L’altezza delle facce
laterali in questo caso viene detta apotema della piramide.
Una piramide è regolare quando è retta e la base è un poligono regolare.
Data una piramide, un piano parallelo alla base e posto ad una distanza dal vertice inferiore all’altezza
individua sulla piramide stessa due solidi : quello cui non appartiene il vertice viene detto tronco di
piramide . Esso è limitato da due poligoni simili tra loro ( basi del tronco ) e da facce laterali che sono
trapezi.
Un poliedro è regolare quando le sue facce sono tutte poligoni regolari congruenti e anche i suoi diedri e i
suoi angoloidi sono congruenti.
Ci sono solo cinque tipi di poliedri regolari :
tetraedro , ottaedro , icosaedro, cubo ( esaedro) e dodecaedro
SOLIDI DI ROTAZIONE
I solidi di rotazione sono generati dalla rotazione di una figura piana attorno ad una retta.
In particolare :
Un cilindro è generato dalla rotazione completa di un rettangolo attorno ad uno dei suoi lati
Un cono è generato dalla rotazione completa di un triangolo rettangolo attorno ad uno dei suoi
cateti
Una sfera è generata dalla rotazione completa di un semicerchio attorno al suo diametro.
Un SOLIDO DI ROTAZIONE corrisponde ad una porzione di spazio percorsa da una figura piana che
ruota su uno dei suoi lati o elementi.
.
La rotazione di altre figure piane più complesse genera infinità di solidi , ma tutti possono venire
ricondotti a combinazioni dei solidi sinora menzionati, con dimensione , posizione ed orientamento
diversi.
ESTENSIONE ED EQUIVALENZA DEI SOLIDI
Due solidi aventi la stessa estensione sono equivalenti.
POSTULATI DELL’EQUIVALENZA DI SOLIDI
1.
2.
3.
4.
Due solidi congruenti sono sempre equivalenti.
Solidi ottenuti come somma o differenza di solidi congruenti o equivalenti sono equivalenti.
Un solido non può essere equivalente ad una sua parte ( postulato di De Zolt ).
Dati due solidi A e B : o è A equivalente a B, o è A prevalente a B ( A > B ) o è A suvvalente a B
( A < B ) . ( legge di esclusione )
5. Due solidi sono equivalenti se possono essere disposti in modo che ogni piano parallelo ad un
altro piano fissato, scelto come riferimento, li tagli secondo sezioni equivalenti ( Principio di
Bonaventura Cavalieri ).