Università degli Studi di Perugia
Facoltà di Ingegneria
Corso di Laurea in Ingegneria Informatica ed
Elettronica
Analisi numerica 3D di dispositivi
fotosensibili per rivelatori di
radiazione
Candidato
Keida Kanxheri
Relatore
Ing. Daniele Passeri
Correlatore
Ing. Stefano Meroli
Anno Accademico 2009 – 2010
… Gjyshes sime Krisanthi,
qe me shume se kushdo tjeter
do te kishte dashur te ishte e pranishme
.
“La teoria è quando si sa tutto e niente funziona.
La pratica è quando tutto funziona e nessuno sa il perché.
Noi abbiamo messo insieme la teoria e la pratica: non c’è niente che funzioni… e nessuno sa il perché!”
Albert Einstein
I Introduzione
1
Fisica dei semiconduttori
Cenno ai Semiconduttori
La configurazione elettronica dell’atomo: elettroni di valenza
La struttura elettronica dei solidi: conducibilità elettrica
La struttura elettronica dei solidi: le lacune elettroniche
Semiconduttori intrinseci ed estrinseci
Ruolo delle impurezze
Giunzione p-n
Giunzione p-n
Applicazioni della giunzione
2
Rilevatori di radiazione
Principio di funzionamento
Modelli di mobilità
Modelli di Generazione e ricombinazione
Separazione dei portatori di carica e generazione di corrente elettrica
Fotodiodo
Active pixel sensors (APS)
3
Strumenti di simulazione
Sentaurus TCAD
Sentaurus Structure Editor
Generazione della Mesh
Sentaurus Device
Risoluzione Numerica
Metodo di Newton
Il file dei comandi
Generazione Ottica
Calcolo della generazione ottica
Inspect
Tecplot sv
Il cluster di calcolo INFN GRID
4
Costruzione del fotodiodo
Generazione della Mesh
5
Simulazioni
Simulazione Quasi-Stazionaria (QS)
Caratteristica I-V del diodo
Variazione del drogaggio di substrato :
Simulazione Tempo-Variante(TV)
Influenza della lunghezza d’onda
Variazione del drogaggio di substrato
Variazione del drogaggio di n-well
I
1
1
1
2
3
5
5
6
8
8
9
10
10
10
11
13
14
15
16
21
21
21
22
24
25
26
28
31
38
40
41
42
43
46
46
52
55
55
57
57
59
61
61
66
73
Variazione della profondità di giunzione
Influenza del contatto metalico
Variazione della potenza del fascio
Variazione del punto di incidenza
Effetti di griglia
CONCLUSIONI E SVILUPPI FUTURI
BIBLIOGRAFIA
74
78
80
82
86
89
91
Introduzione
I
Introduzione
Questo lavoro di tesi si inserisce in un ampio progetto di ricerca, che da anni vede
collaborare il Dipartimento di Ingegneria Elettronica e dell’Informazione dell’Università
degli Studi di Perugia e la sezione di Perugia dell’Istituto Italiano di Fisica Nucleare,
volto allo sviluppo e alla realizzazione di rivelatori di radiazione del sistema di tracciatura
dell’esperimento Compat Muon Solenoid (CMS) in corso di svolgimento presso il Large
Hadron Collider (LHC) del CERN di Ginevra.
Sensori CMOS dedicati alla rivelazione di radiazione sono ormai in produzione
industriale da tempo, e, grazie ad un più favorevole rapporto fra prestazioni e costi, hanno
progressivamente sostituito le architetture CCD in numerose applicazioni; è ragionevole
quindi studiare la possibilità di estendere l’impiego di dispositivi simili alla rivelazione di
particelle cariche, eventualmente modificandone ed ottimizzandone la struttura in
funzione delle specifiche operative e funzionali caratteristiche.
I principi fondamentali di funzionamento di tale classe di sensori sfruttano ancora la
generazione di carica all’interno di un substrato semiconduttore[2]. La tecnologia CMOS,
tuttavia, prevede la presenza di un substrato fortemente conduttivo (necessario alla
prevenzione di fenomeni di latch-up), sul quale viene accresciuto epitassialmente uno
strato di cristallo meno drogato (dello spessore di qualche micrometro), entro il quale
sono realizzati i dispositivi attivi. In pratica, la sola regione utile alla rivelazione è
contenuta entro tale sottile strato epitassiale: non è quindi più necessario svuotare ampi
volumi, eliminando la necessità di elevate tensioni di polarizzazione. La riduzione della
I
Introduzione
carica utile generata dalla radiazione, può essere invece compensata sfruttando
meccanismi di amplificazione locale; tali meccanismi si basano su semplici circuiti attivi
associati a ciascun pixel, compatibili con la tecnologia di fabbricazione, e in grado di
assicurare buone prestazioni in termini di rumore.
I principali vantaggi che potrebbero derivare dall’adozione di sensori CMOS, rispetto alle
tecnologie correntemente utilizzate, possono quindi essere così riassunti:
•
trattandosi di tecnologie ad ampia diffusione commerciale, esse consentono
maggiore economia di fabbricazione;
•
per lo stesso motivo, tali tecnologie sono costantemente e rapidamente aggiornate
verso maggiori densità di integrazione, con il conseguente potenziale incremento
della risoluzione spaziale. E’ ragionevole attendersi, dalle tecnologie correnti,
risoluzioni nell’intorno del m m, da confrontarsi con le risoluzioni, maggiori di
almeno un ordine di grandezza, tipiche dei sensori integrati attualmente utilizzati.
•
E’ possibile la contemporanea integrazione di elementi sensibili e di dispositivi
attivi di buona qualità; inoltre, per questi ultimi e per una ampia varietà di celle
funzionali integrate, sono di norma disponibili modelli e caratterizzazioni
accurate. Ciò semplifica significativamente il progetto e l’implementazione di
elettronica di controllo ed elaborazione di segnale.
•
Inoltre, circuiti realizzati in tecnologie fortemente submicrometriche godono
intrinsecamente di buone caratteristiche di resistenza alla radiazione.
•
E’ possibile realizzare sensori operanti a bassa tensione, con riduzione dei rischi
di breakdown, basse correnti di perdita e basso consumo di potenza.
•
Come sopra ricordato, anche a fronte di una minore estensione del volume
sensibile, esistono prime indicazioni della possibilità di ottenere prestazioni di
rumore ampiamente soddisfacenti: dalla letteratura scientifica e dalle simulazioni
condotte dal nostro gruppo, è possibile prevedere rapporti S/N superiori a 50.
In sintesi, ci si aspetta di potere integrare sensori dotati di maggiore risoluzione spaziale e
di maggiore "intelligenza" locale. Gli strumenti di simulazione utilizzati sono diversi e
II
Introduzione
grazie ad una proficua interazione tra essi sono state effettuate analisi complete e
dettagliate. Fondamentale per tutto ciò è stato l’impiego del cluster di calcolo sito presso
l’INFN di Perugia. Grazie all’immense risorse di calcolo che esso offre, si sono riuscite a
effettuate analisi approfondite e accurate che altrimenti sarebbero state inimmaginabili.
Il contenuto dei vari capitoli è il seguente:
Nel Capitolo 1 è stata data una descrizione generale della fisica dei semiconduttori, della
giunzione p-n e delle sue applicazioni.
Nel Capitolo 2 sono descritti i principi di funzionamento dei rivelatori di
radiazione(APS), ponendo particolare attenzione ai fenomeni di generazione e di
ricombinazione
Nel Capitolo 3 è descritto il pacchetto di simulazione Sentaurus TCAD e il cluster di
calcolo utilizzato per effettuare le varie simulazioni.
Nel Capitolo 4 è descritta la modalità di costruzione del fotodiodo tramite il Sentaurus
Device, la sua geometria e i vari parametri tecnologici e la scelta della mesh migliore al
nostro caso.
Nel Capitolo 5 sono riportate le simulazioni e i risultati ottenuti variando una serie di
parametri tecnologici , parametri di simulazione o caratteristiche del fascio ottico che
incide il fotodiodo.
III
Fisica dei semiconduttori
1
Fisica dei semiconduttori
Un semiconduttore è un materiale isolante a temperature molto basse, ma che ha una
apprezzabile conducibilità elettrica a temperatura ambiente. La distinzione tra un
semiconduttore e un isolante non è molto ben definita; si può dire che un semiconduttore
è un isolante con una banda proibita piccola a sufficienza perché la sua banda di
conduzione sia apprezzabilmente popolata a temperatura ambiente.
Cenno ai Semiconduttori
I semiconduttori hanno iniziato ad assumere importanza nel campo dell'optoelettronica
nel 1953, quando fu dimostrato che nelle giunzioni p-n, se la tensione applicata è
sufficientemente elevata, si ha la moltiplicazione degli elettroni[1]. Questo processo è
dovuto al fatto che gli elettroni sono accelerati al punto tale da avere l'energia sufficiente
a creare nuove coppie elettrone-lacuna (circa una volta e mezza l'energia di gap).
Il meccanismo di moltiplicazione è stato poi sfruttato nel fotodiodo a valanga, che tende a
sostituire il fotomoltiplicatore e che è impiegato come rivelatore nelle comunicazioni
ottiche e nella foto-rivelazione digitale.
La prime cella solare fu realizzata nel 1954. La prima teoria sull'emissione stimolata nei
semiconduttori è del 1961. L'anno seguente divenne chiaro che per ottenere un laser era
necessario impiegare semiconduttori a gap diretto, come il GaAs, e il dispositivo fu
realizzato alla General Electric, all'IBM e nel Lincoln Laboratory.
1
Fisica dei semiconduttori
La configurazione elettronica dell’atomo:
elettroni di valenza
Se consideriamo la struttura atomica degli elementi sappiamo che gli elettroni più interni
occupano sottostrati completi e sono i più legati al nucleo, pertanto non prendono parte ai
fenomeni fisici o chimici, se non all’emissione e all’assorbimento di raggi X.
Gli elettroni più esterni, in genere in un sottostrato incompleto, sono invece responsabili
del legame chimico, dell’interazione degli atomi con la luce, quindi degli spettri di
assorbimento e di emissione, e determinano le proprietà dei materiali. Essi sono detti
elettroni di valenza[3].
Nella formazione delle molecole si ha la transizione da elettroni di valenza localizzati
intorno agli atomi (orbitali atomici) a elettroni distribuiti su tutto lo spazio occupato dalla
molecola (orbitali molecolari). Analogamente nella formazione dei solidi, gli orbitali
atomici si fondono a formare orbitali cristallini, estesi a tutto lo spazio occupato dal
solido. Gli elettroni di valenza nei solidi, dunque, non sono più legati ai singoli atomi, ma
sono de localizzati.
Il cambiamento nella distribuzione della densità elettronica è associato ad una drastica
trasformazione dei livelli energetici discreti degli elettroni di valenza. La struttura dei
livelli energetici del solido si può ottenere partendo da quella dell’atomo isolato,
separando ogni livello relativo ad elettroni di valenza dell’atomo isolato in una
moltitudine di livelli molto vicini, in numero dell'ordine del numero di atomi che
compongono il solido (dell’ordine del numero di Avogadro). A questi elettroni non
corrispondono più singoli livelli discreti di energia, ma moltissimi livelli con valori
vicinissimi l’uno all’altro, ossia distribuiti in modo quasi continuo in un certo intervallo
di energia. A questa distribuzione si dà il nome di banda di energia. Per ogni livello
energetico di partenza si crea quindi una banda di energia all’interno della quale la
distribuzione dei livelli è praticamente continua.
Alcune bande contigue (quelle esterne che sono più larghe) possono sovrapporsi tra loro,
mentre altre possono rimanere separate. La larghezza, in energia, di una banda è
dell'ordine degli eV. L'intervallo fra bande successive, detto intervallo proibito, o gap di
energia, si indica con Eg, il limite superiore della banda di valenza viene indicato con Ev.
2
Fisica dei semiconduttori
Figura 1: Bande di energia
La struttura elettronica dei solidi:
conducibilità elettrica
La conducibilità elettrica di un materiale (σ, espressa in (Ω x m) -1) misura la sua capacità
di trasportare cariche elettriche sotto l’azione di un campo elettrico esterno.
Passando da un materiale ad un altro, la conducibilità elettrica può variare di molti ordini
di grandezza. In genere è possibile individuare quattro categorie principali:
superconduttori: σ ≈ infinita, per T < Tc (temperatura critica)
metalli: σ ≈ 106 ÷104 (Ω x cm)-1
semiconduttori: σ ≈ 103 ÷10-6 (Ω x cm)-1 (a temperatura ambiente)
isolanti: σ ≈ 10-10 ÷10-20 (Ω x cm)-1
Nei solidi cristallini l’enorme variazione della conducibilità dipende dalla configurazione
elettronica dello stato fondamentale del cristallo[3]. I solidi nei quali la banda di valenza e
quelle più interne sono completamente occupate ed esiste un gap di energia Eg abbastanza
grande, si comportano come isolanti.
3
Fisica dei semiconduttori
Il comportamento dei solidi cambia man mano che si considerano cristalli che hanno gap
di energia sempre più piccoli: semiconduttori; se le bande sono parzialmente occupate, si
hanno i conduttori o metalli.
La caratteristica più significativa della conducibilità dei semiconduttori tuttavia non è il
valore, ma la sua forte dipendenza dalla temperatura e dal contenuto di impurezze.
Figura 2: Conducibilità elettrica a temperatura ambiente di varie categorie di materiali
Figura 3: Struttura elettronica dei metalli e degli
4
Fisica dei semiconduttori
La struttura elettronica dei solidi: le lacune
elettroniche
La configurazione elettronica di un solido a temperature diverse dallo zero assoluto è in
generale diversa da quella corrispondente allo stato fondamentale. Nei semiconduttori ad
esempio, per effetto della temperatura può accadere che la banda di valenza non sia
completamente occupata.
Possiamo immaginare che in un livello non occupato della banda di valenza sia presente
una particella immaginaria, detta “buca” o “lacuna”. Una delle conseguenze inaspettate
della teoria delle bande è che questa particella si comporta come se avesse carica elettrica
positiva: sotto l’azione di un campo elettrico esterno accelera nello stesso verso del
campo elettrico applicato[3].
Semiconduttori intrinseci ed estrinseci
Un semiconduttore intrinseco è un semiconduttore sufficientemente puro per cui le
impurità non influiscono apprezzabilmente il suo comportamento elettrico. In questo
caso, tutti i portatori di carica sono dovuti all'eccitazione termica o ottica degli elettroni,
che dalla banda di valenza completa passano alla banda di conduzione, vuota. In questo
modo in un semiconduttore intrinseco c'è lo stesso numero di elettroni e lacune. Gli
elettroni e le lacune, se sottoposti a un campo elettrico, si muovono in direzioni opposte,
ma contribuiscono alla corrente con lo stesso segno, avendo carica elettrica opposta. La
corrente dovuta alle lacune e quella dovuta agli elettroni non è tuttavia necessariamente
uguale in un semiconduttore intrinseco, poiché gli elettroni e le lacune hanno diversa
mobilità elettrica.
La concentrazione di portatori di carica è fortemente dipendente dalla temperatura. Alle
basse temperature, la banda di valenza è completamente piena, rendendo il materiale un
isolante. L' aumento della temperatura porta ad un aumento del numero di portatori di
carica e ad un corrispondente aumento della conduttività. Questo principio è usato nei
termistori. Questo comportamento contrasta nettamente con quello della maggior parte
5
Fisica dei semiconduttori
dei metalli, che tendono a essere meno conduttivi alle alte temperature a causa
dell'aumento dello scattering dei fononi.
Un semiconduttore estrinseco è un semiconduttore che è stato drogato con impurità per
modificare il numero e il tipo dei portatori liberi di carica.
Ruolo delle impurezze
La presenza di impurezze, in proporzioni strettamente controllate, in un cristallo
semiconduttore ne modifica il comportamento; esse consentono di controllare la
concentrazione degli elettroni e delle lacune responsabili delle proprietà elettriche. Infatti
la concentrazione di elettroni e lacune in un semiconduttore puro non sarebbe sufficiente
a fornire le densità di corrente necessarie per gli impieghi nei dispositivi[3]. Le impurezze
utili nei semiconduttori sono di due tipi: donatori e accettori. La loro presenza provoca la
comparsa, all’interno del gap proibito, di livelli d’energia che possono essere occupati
dagli elettroni. Per realizzare i dispositivi elettronici donatori o accettori sono aggiunti
intenzionalmente al semiconduttore mediante processi di drogaggio. È sufficiente una
concentrazione piccola di impurezze per alterare profondamente le proprietà elettriche, ad
esempio una parte per miliardo. Il donatore è un’impurezza che cede facilmente (“dona”)
uno dei suoi elettroni di valenza alla banda di conduzione del semiconduttore. Un
donatore tipico è il fosforo (pentavalente) in un cristallo di silicio o di germanio
(tetravalenti): quattro degli elettroni del fosforo contribuiscono al legame tetraedrico
tipico degli elementi del IV gruppo, mentre il quinto elettrone non è legato agli atomi del
semiconduttore adiacenti, ma è debolmente legato allo ione P+. Il livello di energia
dell’elettrone del P in un cristallo di silicio è all'interno del gap, 0.0044 eV (= ED) al di
sotto della banda di conduzione. L’energia dell’elettrone localizzato in prossimità del
fosforo è quindi molto più vicina alla banda di conduzione rispetto all’energia degli
elettroni della banda di valenza. Di conseguenza è sufficiente una piccola agitazione
termica per farlo saltare nella banda di conduzione: alla temperatura ambiente le
oscillazioni del reticolo hanno ampiezza sufficiente per “promuovere” gli elettroni di
quasi tutti i donatori alla banda di conduzione. Il semiconduttore è detto "di tipo n ",
perché i portatori sono gli elettroni, di carica negativa. Un analogo discorso vale se invece
6
Fisica dei semiconduttori
dei donatori sono presenti impurezze accettori, come ad esempio il boro che è trivalente. I
tre elettroni di valenza del boro sono legati in modo covalente a tre atomi di silicio
adiacenti, lasciando vacante il legame con il quarto atomo. Questo equivale a dire che una
lacuna sta intorno al boro. Se un elettrone della banda di valenza si muove ad occupare
questo legame vacante, si crea una lacuna nella banda di valenza. Allora i portatori
maggioritari sono le lacune e il semiconduttore è detto "di tipo p", perché le lacune si
comportano come particelle di carica positiva. Nel caso generale in cui siano presenti sia
donatori che accettori, nel semiconduttore avviene un processo di compensazione che
porta ad una concentrazione efficace di drogante uguale al modulo della differenza tra le
due concentrazioni di droganti.
Figura 4: Silicio drogato con Fosforo
7
Fisica dei semiconduttori
Giunzione p-n
Un semiconduttore omogeneo, ossia con caratteristiche uniformi al suo interno, ad una
data temperatura si comporta come una normale resistenza, sia esso puro (intrinseco), o
drogato[1]. Le applicazioni pratiche dei semiconduttori in generale non si basano su
materiali omogenei, ma su monocristalli nei quali è stata artificialmente creata una
variazione nel drogaggio più o meno brusca: una giunzione p - n, che separa due zone di
diversa concentrazione di portatori (elettroni o lacune) e di cariche fisse (impurezze
ionizzate).
Figura 5: schema di drogaggio
Al campo elettrico che si crea al contatto fra le due zone con conducibilità di tipo diverso
si devono le importanti caratteristiche elettriche della giunzione. Lo
spessore d dello strato di svuotamento diminuisce al crescere del
drogaggio. Lontano dalla giunzione, oltre la zona di svuotamento, il
campo elettrico interno si annulla e la concentrazione dei portatori ha
gli stessi valori che si hanno nel semiconduttore di tipo p o di tipo n
in assenza di giunzione.
Quando alla giunzione è applicata una tensione esterna V, l’equilibrio
viene alterato e attraverso la giunzione si stabilisce un flusso di
portatori di carica la cui intensità dipende fortemente dal segno della
tensione applicata. Dato il carattere asimmetrico della giunzione p-n
Figura 6:
sono infatti possibili due configurazioni distinte: una in cui la
tensione esterna aumenta il potenziale elettrico della parte n e la condizione opposta, in
8
Fisica dei semiconduttori
cui la parte p viene posta a potenziale maggiore. La prima condizione, corrisponde
(convenzionalmente V < 0) alla giunzione polarizzata in modo “inverso”, il flusso dei
portatori scende praticamente a zero ed è pressoché indipendente dal valore del potenziale
applicato. Nella condizione opposta, la giunzione è “polarizzata direttamente” (V > 0): la
barriera è ora inferiore rispetto al caso di equilibrio e l’intensità della corrente cresce
rapidamente all’aumentare del campo applicato.
Diminuire la barriera alla giunzione equivale a favorire la corrente di diffusione rispetto a
quella drift. La forte asimmetria nel comportamento della giunzione, è spiegabile col fatto
che, mentre la corrente di drift è proporzionale alla concentrazione dei minoritari, la
corrente di diffusione dipende dalla concentrazione dei maggioritari il cui valore è
enormemente più grande.
Applicazioni della giunzione
Una struttura costituita da una giunzione p - n con contatti ohmici agli estremi delle zone
neutre p ed n è detto diodo a giunzione p - n. La caratteristica corrente-tensione è
fortemente asimmetrica. Con polarizzazione diretta la corrente cresce esponenzialmente,
mentre con polarizzazione inversa satura ad un valore molto piccolo.
La giunzione p - n svolge un ruolo importante nell’elettronica e come elemento per la
costruzione dei transistor[2]. Inoltre la giunzione è l’elemento costitutivo dei dispositivi
optoelettronici, per l’emissione e la rivelazione della radiazione, delle celle solari che
convertono l’energia ottica in energia elettrica, e dei dispositivi a microonde.
Figura 7: esempio di dispositivi optoelettronici
9
2
Rilevatori di radiazione
Un fotorivelatore è un dispositivo che, investito da una radiazione luminosa di una
specifica lunghezza d’onda, è in grado di convertire tale radiazione luminosa in una
corrente elettrica di valore proporzionale all’ intensità della radiazione luminosa
incidente. Esistono diverse tipologie di fotorivelatori, che si differenziano per il fatto di
offrire prestazioni e gamma spettrale di funzionamento diverse tra di loro. Nel presente
capitolo si analizzerà il funzionamento di un semplice fotodiodo e la sua applicazione
come elemento sensibile nei sensori di immagine a pixel attivi (APS)[4].
Principio di funzionamento
Il funzionamento dei rivelatori di particelle a semiconduttore si basa sulla capacità di una
particella di cedere energia al cristallo di silicio attraverso la ionizzazione di uno o più
atomi. In questo modo l’atomo libera uno dei suoi elettroni, solitamente uno di quelli che
risiedono negli orbitali più esterni, che è quindi libero di muoversi all’interno del reticolo.
Rivelatori di radiazione
Figura 8: semplificazione del fenomeno della fotoionizzazione
In altre parole si forma una coppia elettrone–lacuna. Se nella regione in cui la coppia si
viene a formare è presente un campo elettrico, i portatori possono essere separati in modo
che non vengano a ricombinarsi immediatamente ed anzi accelerati verso i due elettrodi
che impongono una differenza di potenziale, inducendo un segnale che potrà essere letto
dall’elettronica collegata.
Modelli di mobilità
La mobilità di un portatore di carica situato in un materiale è un parametro che mette in
relazione la velocità media vd della particella con il campo elettrico E a cui essa è
soggetta[1]. La relazione tra le due grandezze è in generale piuttosto complessa, ma in
certi casi, in particolar modo per basso campo, può essere ridotta ad una semplice
relazione del tipo:
Vd = µE
µ rappresenta appunto la mobilità; essa si esprime in m2/(V·s), in unità del Sistema
Internazionale.
In un materiale sottoposto a campo elettrico, un portatore di carica è si soggetto all'azione
di quest'ultimo, ma anche a continue interazioni con il mezzo medesimo. In un cristallo
ad esempio, un elettrone urta costantemente sia contro le impurezze della struttura, che
contro le vibrazioni indotte in essa dall'agitazione termica del materiale. Tutto questo
obbliga la particella a percorrere una traiettoria caotica, descritta tipicamente come un
11
Rivelatori di radiazione
moto browniano, ma comunque dotata di una ben precisa componente osservabile (quella
rilevata dagli strumenti, e a cui si associa appunto la velocità media) che dipende
unicamente dal campo elettrico, dalle caratteristiche del materiale e dalle proprietà
statistiche degli "ostacoli", come la temperatura. Questi due ultimi aspetti vengono riuniti
nel parametro di mobilità.
Per quanto detto, la mobilità dipende da un certo numero di fattori. Tra questi va anche
citato il genere di portatori. In un mezzo infatti possono essere presenti molti tipi diversi
di particelle che contribuiscono alla conduzione elettrica, e ciascuno di essi interagisce
con il materiale e con il campo elettrico in maniera caratteristica. Ad esempio, portatori
più pesanti risponderanno alla perturbazione con una maggiore inerzia, muovendosi cioè
più lentamente. In un cristallo, in cui la massa efficace della particella dipende dalla
banda in cui si trova, si riscontreranno quindi differenti parametri di mobilità; il caso
tipico è quello di un semiconduttore, nel quale si individuano due coefficienti, uno per gli
elettroni e l'altro per le lacune. Un modello semplice, che trascura l'interazione con il
cristallo ma considera solamente quella con il campo elettrico e le impurezze, conduce
alla seguente espressione della mobilità
µ=
qτ
m
dove q è la carica del portatore (1,6 · 1019 C nel caso dell'elettrone o della lacuna), m la
sua massa e τ il tempo libero medio di collisione, ossia il tempo che intercorre in media
prima che una particella scelta a caso collida. Questa espressione è valida anche in altri
contesti simili, ad esempio nei plasmi.
Dalla regola di Matthiessen [3] per i tempi di collisione, segue una formula analoga per le
mobilità imputabili a cause indipendenti d'urto A e B (ad esempio, collisioni contro difetti
di struttura e vibrazioni termiche)
1
µ
=
1
µA
+
1
µB
In un semiconduttore, la mobilità dipende dalle caratteristiche del materiale, dal tipo di
portatore di carica, dalla concentrazione di impurezze (ad esempio, dal drogaggio) e dalla
temperatura. Per alto campo inoltre, la relazione di proporzionalità diretta non è più
valida e il parametro dipende a sua volta dal campo elettrico; questo fatto dà luogo al
12
Rivelatori di radiazione
cosiddetto fenomeno della saturazione di velocità, particolarmente importante nei
dispositivi in cui sono rilevanti le correnti di deriva come i MOSFET.
Intensi studi sono stati condotti al fine di ottenere adeguati modelli descrittivi a riguardo e
componenti elettronici con mobilità dei portatori elevata. Si noti infatti che un dispositivo
ad alta mobilità conduce correnti maggiori, permettendo di conseguenza una migliore
risposta sia in termini di potenza che in termini di velocità.
Modelli di Generazione e ricombinazione
Quando un fotone colpisce un pezzo di silicio, due cose possono accadere: il fotone
attraversa indisturbato il materiale o viene assorbito[1].
Nel primo caso, l’energia del fotone è inferiore al bandgap del silicio, mentre nel secondo
caso esso può cedere la propria energia a un elettrone del reticolo cristallino.
Generalmente, tale elettrone si trova nella banda di valenza, fermamente legato
covalentemente, tra atomi vicini e perciò incapace di allontanarsene. L’energia cedutagli
dal fotone lo eccita portandolo nella banda di conduzione dove è libero di muoversi
all’interno del semiconduttore.
Il legame covalente da dove proveniva l’elettrone, ora possiede una lacuna, permettendo
così agli elettroni dei legami vicini di occuparla, lasciando una buca dietro di sé: la lacuna
può così muoversi a sua volta all’interno del semiconduttore. In questo modo,
l’assorbimento di un fotone genera quelle che sono chiamate coppie elettrone-lacuna.
Come abbiamo detto, occorre solo che il fotone possieda un’energia superiore al bandgap
del silicio affinché possa promuovere un elettrone dalla banda di valenza a quella di
conduzione; la radiazione proveniente dal sole è costituita per la maggior da fotoni con
energie molto maggiori del gap del silicio e questa energia in eccesso viene convertita in
calore piuttosto che in corrente utilizzabile. Per capire il funzionamento di un rivelatore di
radiazione bisogna andare a vedere nella profondità della giunzione p-n. Ciò che avviene
è un processo di diffusione degli elettroni dalla regione ad alta concentrazione di elettroni
– il lato n della giunzione – verso la regione a bassa concentrazione – il lato p della
giunzione: una volta attraversata la giunzione p-n, essi si ricombinano con le lacune del
lato p. Questa diffusione dei portatori di carica non avviene indefinitamente nel tempo a
causa del campo elettrico che si instaura per lo sbilanciamento di carica che questa stessa
diffusione crea da entrambi i lati della giunzione. Gli elettroni provenienti dagli atomi di
13
Rivelatori di radiazione
drogante nel lato n della giunzione diffondono nel lato p lasciando dietro di sé nuclei
carichi positivamente, lasciando cioè un eccesso di carica positiva sul lato n della
giunzione; contemporaneamente, questi elettroni occupano le lacune sul lato p creando un
eccesso di carica negativa su tale lato. Il campo così prodotto si oppone all’ulteriore
diffusione di portatori di carica attraverso la giunzione: questa zona della giunzione, dove
non vi sono portatori di carica mobili, è chiamata regione di svuotamento.
Separazione dei portatori di carica e generazione di corrente
elettrica
Una volta che la coppia elettrone-lacuna è stata generata dall’assorbimento di un fotone,
sia l’elettrone che la lacuna sono entrambi liberi di muoversi in maniera indipendente
all’interno del reticolo del silicio. Il campo elettrico nella giunzione porterà gli altri nel
lato n e le buche nel lato p[5].
Contatti ohmici vengono applicati a entrambi i lati p ed n della cella e connessi ad un
carico esterno: gli elettroni creati nel lato n, o raccolti dalla giunzione e spinti nel lato n,
possono così raggiungere il carico ed alimentarlo, proseguendo quindi fino a raggiungere
il contatto al lato p della cella (vedi fig 9).
Figura 9: Schema di principio del funzionamento di un rivelatore
Come mostrato in figura 9 una particella attraversa la regione svuotata e genera un certo
numero di coppie elettrone-lacuna. Le lacune vengono accelerate nella direzione del
campo e quindi raccolte dall’elettrodo p+.
Gli elettroni si muovono in direzione opposta e vengono raccolti dall’elettrodo n+.
Dato che gli elettroni possiedono una mobilità maggiore, la lettura del segnale
avviene dal lato n.
14
Rivelatori di radiazione
Fotodiodo
Le tecniche più moderne per rivelare il campo elettromagnetico si basano sull’interazione
del campo con i semiconduttori[4]. Ogni fotone che incide su una parte di semiconduttore
intrinseco viene in teoria assorbito, producendo una coppia elettrone-lacuna nel materiale.
Tale coppia, sotto l’effetto di un campo elettrico esterno, contribuisce alla corrente di
fotoconduzione. Ogni tipo di rivelatore fotoconduttivo ha bisogno, per segnalare la
presenza della radiazione luminosa, di una polarizzazione esterna. In particolare, in
assenza di radiazione incidente, la corrente nel circuito di polarizzazione esterno è
praticamente nulla, poiché il semiconduttore intrinseco ha un basso valore di conduttività.
Al contrario, in presenza di una radiazione incidente con potenza utile, il numero di
portatori generati per assorbimento può diventare rilevante: la corrente assume allora
valori apprezzabili, causando un’elevata caduta di tensione.
Figura 10: Schema di un fotodiodo a giunzione.
Come si nota dalla figura 10 il fotodiodo è una semplice giunzione p-n polarizzata in
inversa. Quando questa giunzione è illuminata da un flusso di fotoni di frequenza
opportuna essi penetrano nel materiale e vengono assorbiti. In questa regione si ha
generazione di coppie elettrone-lacuna, ma, affinché esse generino una corrente, è
necessario che vengano trasportate in una particolare direzione. E necessaria quindi la
15
Rivelatori di radiazione
presenza di un campo elettrico. L’unica regione della giunzione in cui esso è presente è la
regione svuotata. Questa è la regione in cui è preferibile che avvenga la generazione.
Le
coppie
elettrone-lacuna
generate
nella
regione
di
svuotamento
vengono
immediatamente separate dal campo elettrico. Quando giungono nelle due regioni quasi
neutre possono anche ricombinarsi; le cariche di segno opposto con cui si ricombinano
devono essere fornite direttamente o indirettamente dal generatore, quindi si ha la
corrente.
Può succedere che le coppie elettroni lacune vengano generate nelle zone neutre, ma in
prossimità della zona di svuotamento;esse possono, per diffusione, giungere nella zona
svuotata prima di ricombinarsi. Qui il campo elettrico porta elettroni o lacune nell’altra
zona rapidamente. La separazione dà un contributo di corrente.
Gli elettroni e le lacune delle coppie che vengono generate nelle zone neutre, lontano
dalla zona di svuotamento, si muovono randomicamente finché non si ricombinano. La
ricombinazione di elettroni e lacune avviene nella stessa zona neutra, quindi non dà un
contributo di corrente. Si ha solo un aumento dei portatori, quindi un aumento della
conducibilità
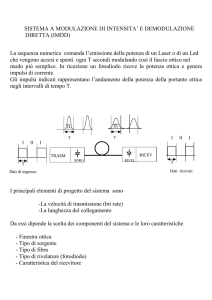
Active pixel sensors (APS)
Un sensore d'immagine APS è costituito da un circuito integrato composto da un array di
sensori pixel, in cui ogni pixel contiene a sua volta un fotodetector ed un amplificatore[5].
Negli ultimi anni lo sviluppo della ricerca sulla tecnologia CMOS, ha fatto in modo che i
sensori basati su questa tecnologia subissero un miglioramento costante e tuttora in
avanzamento e per questo motivo tale tecnologia è riuscita a prevalere su molte altre, per
la progettazione di rivelatori di radiazione. All'inizio, erano penalizzati dal fatto che
rispetto ai Charge-Coupled-Devices (CCD), ai Silicon Drift Detectors (SDD) ed ai
sensori gassosi, risultavano essere più rumorosi e caratterizzati da una minore efficienza
di raccolta. Tuttavia grazie al costante avanzamento della tecnologia CMOS, spinto dal
loro impiego nell'elettronica di consumo, è stato possibile correggere questi difetti e
renderli secondari rispetto agli innumerevoli vantaggi riassumibili nei seguenti punti:
1. basso costo e tecnologia facilmente disponibile,
2. basso consumo di potenza,
16
Rivelatori di radiazione
3. utilizzo di basse tensioni di alimentazione (<5V),
4.alta risoluzione dovuta al costante scaling della tecnologia CMOS
5. possibilità di inserimento di elettronica digitale e analogica sullo stesso chip del
sensore, per ottenere un sistema di acquisizione più compatto.
Figura 11: schema di un APS
.
I sensori di tipo CMOS richiedono di dedicare una certa area del sensore all'elettronica di
supporto, in modo da ridurre l'impatto del rumore sui valori misurati. Per questo motivo
l'architettura dei dispositivi CMOS APS prevede l'integrazione sullo stesso chip
dell'elemento sensibile e della circuiteria per l'amplificazione e per l'indirizzamento del
segnale. Il vantaggio di una implementazione di questo tipo è l'aumento della velocità di
lettura e la riduzione del rumore a causa del minore impatto dei parassiti.
Figura 12: Struttura di un APS
Il prezzo da pagare è la riduzione del Fill Factor(FF), dovuta alla presenza sul pixel di
aree non sensibili, in quanto occupate dall' elettronica. In particolare risulta molto utile la
17
Rivelatori di radiazione
possibilità di costruire in maniera integrata sullo stesso chip il sensore d'immagine e tutta
la circuiteria di rilevazione, amplificazione ed elaborazione del segnale. La tecnologia
CMOS ha infatti ormai raggiunto un grado di integrazione notevolmente superiore
rispetto a quello delle altre tecnologie e questo non può che essere un elemento a suo
favore in un periodo in cui la corsa alla miniaturizzazione e all'integrazione è ormai
diventata inarrestabile[5].
Il principio su cui si basa il funzionamento di un singolo pixel di un sensore CMOS, è
quello dell'assorbimento di radiazione, che si manifesta all'interno di una semplice
giunzione p-n polarizzata in inversa: il fotodiodo.
I fotodiodi utilizzati hanno dimensioni dell'ordine del micron e ciò comporta
inevitabilmente un'estensione della giunzione p-n molto ridotta e, di conseguenza, un'area
sensibile piuttosto piccola.
D'altro canto fotodiodi di dimensioni micrometriche, consentono risoluzioni dello stesso
ordine di grandezza e dunque maggiore precisione.
Le basse tensioni di alimentazione impongono dei limiti superiori alle tensioni di
polarizzazione inversa e ciò provoca una riduzione della regione svuotata del fotodiodo.
Tuttavia le basse tensioni di alimentazione permettono di ridurre il consumo di potenza,
oltre che a prevenire rischi di break down.
L'idea dunque è quella di sfruttare i vantaggi per eliminare gli svantaggi.
Ad esempio, per poter far fronte alle carenze nelle risposte dei fotodiodi, è possibile
inserire una rete di amplificazione locale del segnale. Come detto precedentemente, i
fotodiodi sono inseriti nelle strutture dette pixel ed ogni pixel ha una struttura tale da
isolare ed amplificare i segnali in uscita dal fotodiodo. Questo è il motivo per cui tali
strutture vengono indicate con il nome di Active Pixel Sensors (APS). I pixel APS in
realtà esistono già da diversi anni, sfruttati in maggioranza per applicazioni per il visibile;
il tentativo che si sta portando avanti è quello di sfruttarne le proprietà nel campo dei
sensori di radiazione.
18
Rivelatori di radiazione
Figura 13:Schema circuitale di un pixel APS
Figura 14: Architettura di base di un sensore a pixel CMOS
Il principio di funzionamento sfruttato è quello dell’integrazione di carica. Al transistor di
reset (M1) è applicato un segnale periodico di reset, con un duty cycle variabile, in modo
da permette al diodo di polarizzarsi in inversa dato che la tensione al catodo del fotodiodo
raggiungerà il valore di Vdd-Vth, con Vth tensione di soglia del transistore di reset (dato
che gli nmos degradano i segnali alti). Quando il segnale di reset torna al livello logico
basso, dapprima la tensione del nodo scende (di poche decine di mV), a causa degli
accoppiamenti capacitivi con il gate del MOS di reset. Se a tal punto non si ha il
passaggio di una particella, la tensione del catodo del fotodiodo si mantiene costante,
trascurando la piccola diminuzione dovuta alla sola corrente al buio[5].
19
Rivelatori di radiazione
Figura 15:Andamento temporale di un pixel quando colpito da un fotone X
Nel caso in cui si verifica un evento, ovvero la particella ionizzante impatta la regione
sensibile, la tensione del fotodiodo diminuisce notevolmente (di alcune centinaia di mV)
a causa del flusso di portatori generati. La variazione di tensione ottenuta viene riportata
al nodo di OUT del source follower (M2), dove viene letta, prima dell’applicazione
successiva del reset, ottenendo le informazioni sul passaggio della particella.
20
3
Strumenti di simulazione
Gli strumenti di simulazione tecnologica (Technology CAD) sono usati, da tutte le
industrie che si occupano di semiconduttori, in quanto permettono di ridurre i costi,
velocizzare il processo di ricerca e sviluppo, ed ottimizzare il processo di produzione dei
semiconduttori e dei dispositivi. Mediante simulazioni svolte al computer, sempre più
veloci ed accurate, è possibile testare la funzionalità e l'utilità di un dispositivo, prima
ancora di realizzarne fisicamente il prototipo, riducendo così i costi di progetto. Infatti, si
indaga il comportamento assunto dal dispositivo in condizioni che riproducano quanto
più fedelmente possibile, quelle di reale funzionamento, per ottenere risultati realistici e
con un alto livello di accuratezza.
Sentaurus TCAD
Sentaurus TCAD opera in ambiente Linux ed è un avanzato strumento software, parte
della completa suite di prodotti Synopsys TCAD (Technology Computer-Aided Design),
utile dalla fase di progetto a quella di ottimizzazione di dispositivi a semiconduttore. Esso
è in grado di valutare strutture da una a tre dimensioni e di simulare le caratteristiche
elettriche, termiche ed ottiche di un ampia gamma di dispositivi a semiconduttore[6]. Al
suo interno comprende la definizione di robusti metodi numerici di risoluzione e modelli
fisici avanzati, combinabili arbitrariamente a seconda dell'occorrenza, che consentono di
Strumenti di simulazione
simulare un vasto campo di strutture, dalle tecnologie submicrometriche MOS fino a
quelle bipolari di potenza e anche sofisticate eterosrutture. Alcuni dei grandi punti di
forza derivanti dall'utilizzo di strumenti TCAD, sono sicuramente la riduzione dei tempi
di sviluppo, una rapida ottimizzazione delle prestazioni dei dispositivi, veloce
prototipazione e l'analisi di nuovi concetti di dispositivo, per i quali i processi di
fabbricazione non sono stati ancora definiti.
Ovviamente un dispositivo virtuale è un approssimazione di un dispositivo reale, per
questo motivo è stato scelto di effettuare simulazioni tridimensionali, piuttosto che
bidimensionali, al fine di ridurre tale livello di approssimazione. Infatti uno dei limiti
delle simulazioni di strutture bidimensionali, è che il simulatore considera il movimento
dei portatori solamente lungo la direzione della lunghezza e della profondità, assumendo
la larghezza per convenzione pari ad 1 µm. E ovvio che un approccio di questo genere,
pur semplificando i calcoli e riducendo drasticamente i tempi di elaborazione, introduce
necessariamente delle imprecisioni nella descrizione del comportamento del dispositivo.
Durante lo svolgimento di questo lavoro è stato approfondito l'utilizzo di alcuni software
compresi all'interno pacchetto stesso:
1.
2.
3.
4.
Sentaurus Structure Editor
Sentaurus Device
Inspect
Tecplot
Sentaurus Structure Editor
Sentaurus Structure Editor è risultato utile per la creazione del layout della struttura, la
definizione dei profili di drogaggio, dei contatti e la generazione di mesh, ovvero di
griglie di discretizzazione del dispositivo[7]. Tali operazioni si possono effettuare per via
grafica o inserendo istruzioni, che il software è in grado di leggere ed eseguire, nella riga
di comando.
22
Strumenti di simulazione
Figura 16:Finestra di lavoro di Sentaurus Structure Editor
Figura 17:Esempio di struttura costruita in 3D su Sentaurus Structure Editor
Consente tre distinti modi di operare: creazione delle strutture in 2D, 3D, ed emulazione
dei processi in 3D.
23
Strumenti di simulazione
I modelli 2D e 3D dei dispositivi, vengono creati geometricamente partendo da strutture
elementari, come rettangoli, poligoni, cubi, cilindri, e sfere. Le forme più complesse
vengono generate invece, a seguito dell'intersezione degli elementi primari[8].
Generazione della Mesh
Una volta definita la struttura ed impostati tutti i profili di drogaggio, è necessario
generare la Mesh del dispositivo prima di poterlo simulare, ovvero è necessario applicare
una griglia di discretizzazione alla struttura, che la renderà rappresentabile da un numero
finito di punti nello spazio[9]. Questa fase di progetto assume un ruolo estremamente
importante, in quanto è direttamente legata alla qualità dei risultati che si andranno ad
ottenere. Per riuscire a simulare correttamente il comportamento di un dispositivo, è
necessario risolvere equazioni particolarmente complesse, che non verranno però risolte
su tutto il dominio della struttura in maniera continua, ma solamente in corrispondenza
dei punti della Mesh. Questi sono gli unici
punti in cui si tiene memoria delle
caratteristiche del dispositivo, come materiale costitutivo, profili di drogaggio.
Di conseguenza per ottenere una descrizione sufficientemente accurata, è necessario
avere una griglia piuttosto fitta; il problema è che ciò comporterebbe una complessità
computazionale di calcolo eccessiva, mentre si deve far fronte alla necessitµa di risolvere
le equazioni in tempi ragionevoli. E’ importante quindi scegliere il giusto numero di
punti, mediante una soluzione di compromesso, senza perdere però di vista l'accuratezza e
l'affidabilità del risultato.
Figura 18:Generazione di mesh in 3D
Si procede quindi progettando una griglia più fitta in corrispondenza delle zone di
giunzione, dove si hanno bruschi cambi di grandezze fondamentali come la
24
Strumenti di simulazione
concentrazione degli atomi di materiale drogante (doping). Nel resto della struttura, in cui
le caratteristiche risultano più omogenee, è sufficiente una griglia con punti
maggiormente distanziati tra loro. Va comunque sempre tenuto in considerazione che non
è possibile definire una griglia ottima per tutti i dispositivi, ma ogni struttura e ogni tipo
di situazione faranno di volta in volta preferire una griglia rispetto ad un'altra.
Sentaurus Device
Sentaurus Device è un solutore matematico che simula numericamente il comportamento
elettrico di un singolo dispositivo a semiconduttore isolato o di numerosi dispositivi
combinati in un circuito. Esso facendo riferimento alla mesh, applica le equazioni dei
semiconduttori e le condizioni al contorno in forma discreta e risolve[7]. Le varie
grandezze elettriche (come le correnti, le tensioni, etc.) sono calcolati sulla base di una
serie di modelli matematici che esprimono la realtà fisica e descrivono la distribuzione
dei portatori di carica ed i meccanismi di conduzione. Questi modelli sono i seguenti:
∇ • (− ε∇φ ) = q p − n + N + + N −
d
a
dn
∇ • j e = q R − G +
dt
dp
− ∇ • j n = q R − G +
dt
(
)
dove:
Nd: concentrazione di atomi donatori
Na: concentrazione di atomi accettori
G ed R: tasso di generazione e di ricombinazione dei portatori liberi
je e jh: densità di corrente di elettroni e di lacune
n e p: concentrazione degli atomi e delle lacune
Φ: potenziale elettrostatico
Sentaurus Device possiede uno schema di approssimazione, che gli consente di calcolare
il potenziale quasi Fermi relativo ad elettroni e lacune, da cui applicando ben note
formulazioni, si può risalire alla concentrazione delle cariche stesse all'interno di una
25
Strumenti di simulazione
struttura. Il diodo, costituito da un substrato di tipo p ed una giunzione n+, quando si
trova in condizione di equilibrio dinamico, presenta un potenziale di riferimento collocato
in una posizione intermedia tra la banda di conduzione e la banda di valenza, il potenziale
di Fermi. Fuori dall'equilibrio, come ad esempio a seguito di un illuminazione laser, si
vorrebbe poter ancora avere dei livelli energetici di riferimento che permettano di
ricavare la concentrazione di maggioritari e minoritari. Per questo motivo, si individuano
non più uno, ma due potenziali, il livello quasi-Fermi per elettroni ed il livello quasiFermi per lacune.
Se ad esempio si considera come statistica di occupazione dei livelli energetici, la
relazione di Boltzmann:
E − EC
n = N C • exp F ,n
kT
,
Ev − E F , p
p = N v • exp
kT
E F , n = − qφ n
,
E F , p = − qφ p
n e p rappresentano rispettivamente la concentrazione di elettroni e lacune
Nc ed Nv sono le effettive densità degli stati
EF,n ed EF,p rappresentano i livelli quasi-Fermi per elettroni e lacune
Φn e Φp sono i potenziali quasi-Fermi rispettivamente per elettroni e lacune
Ec ed Ev sono rispettivamente il livello energetico inferiore della banda di conduzione ed
il livello energetico superiore della banda di valenza.
Risoluzione Numerica
Sentaurus Device risolve numericamente il sistema di equazioni alle derivate parziali,
ossia le equazioni di Poisson e di continuità per elettroni e lacune, che descrivono il
comportamento dei portatori di carica elettrica, la conservazione della carica e il
potenziale elettrico[7]. Le incognite del sistema, la densità di elettroni e lacune ed il
valore del potenziale elettrico, vengono calcolate suddividendo l’area del dispositivo in
tanti piccoli triangoli:
26
Strumenti di simulazione
Figura 19: metodo Box Discretization
In generale un volume cosi costruito è in grado di discretizzare un’equazione del tipo:
r
∇• j + R = 0
In un’equazione del tipo:
∑k
j ≠i
ij
• jij + µ (Ω j ) • ri
A seconda che si lavorando in una, due o tre dimensioni e a seconda dell’equazione
considerata, ogni parametro assume un valore ed una forma diversi.
Ciascuna equazione viene integrata sopra un poligono, che racchiude ciascun nodo
eguagliando il flusso all'interno del poligono con i pozzi e le sorgenti della grandezza
analizzata, in modo da conservare la corrente e il flusso elettrico.
La discretizzazione delle equazioni dà luogo ad equazioni algebriche non lineari
accoppiate, le quali devono essere risolte con un metodo iterativo non lineare, come quelli
di Gummel o di Newton. Entrambi questi metodi risolvono sistemi lineari di equazioni da
uno a tre volte il numero dei punti della griglia. Il carico computazionale di una
simulazione è il prodotto del numero di soluzioni matriciali per il costo di ciascuna
soluzione: l’obiettivo dei vari metodi è quello di trovare il giusto compromesso tra l’una o
l’altra componente.
La scelta del metodo più adatto dipende dalla particolare applicazione, poiché nessuno dei
due metodi risolutivi può essere considerato il migliore per tutti i casi.
Nel lavoro in esame, viene utilizzato il metodo di Newton che è quadratico, mentre quello
di Gummel è lineare nella maggior parte dei casi. Infatti l’interazione non lineare
27
Strumenti di simulazione
generalmente converge o con tasso lineare o quadratico: nel primo caso l’errore cala dello
stesso fattore ad ogni iterazione, mentre nel secondo l’errore diminuisce con tasso
quadratico, dando una più rapida convergenza. Quindi per soluzioni più accurate il
metodo quadratico è il migliore.
Sentaurus Device può utilizzare sia il metodo di Newton sia il metodo di Gummel:
il metodo di Gummel effettua una risoluzione disaccoppiata, nel senso che un certo
numero di variabili è tenuto fisso mentre se ne vengono risolte altre. L'equazione non
lineare di Poisson viene risolta con un ciclo di Newton, assumendo fissati i livelli di
Fermi.
Metodo di Newton
Tale metodo effettua una risoluzione accoppiata per risolvere il sistema non lineare g(z) =
0:
r rv
g + gx = 0
r
v
z j − z j +1 = λx
dove λ è definita in maniera tale che g k +1 ∠ g k e più vicino possibile al valore 1.
Le iterazioni di tale sistema terminano quando vengono soddisfatti i criteri di
convergenza, che in Sentaurus Device sono due:
1. La norma del vettore g, indicata come right-hand side (RHS)
2. L'errore relativo della variabile calcolata definito come
λx
z
Il calcolo dalla convergenza secondo questo criterio viene effettuato tramite la
seguente formula:
1
εR
•
z (e, i, j ) − z (e, i, j − 1)
1
∑
N e ,i
z (e, i, j ) + z ref (e )
28
Strumenti di simulazione
Figura 20: Iterazioni di Newton
in cui z(e, i, j) è soluzione dell' equazione e, al nodo i-esimo nell' interazione j-esima. La
costante N è data dal numero totale dei nodi moltiplicato per il numero di equazioni.
Mentre il parametro εR è l'errore relativo. Il valore di riferimento zref assicura la stabilità
numerica quando z(e,i,j) è zero o molto piccola[7]. Questa condizione di errore assicura
che le rispettive equazioni siano risolte con una precisione di circa zref (e) εR[.
Un dispositivo a semiconduttore reale è rappresentato nelle simulazioni come
un dispositivo virtuale le cui proprietà sono discretizzate su di una griglia non
uniforme di nodi. In quest’ottica quindi un dispositivo virtuale è una versione
discretizzata, e dunque approssimata, di quello reale. L’impossibilità da parte di
un computer di gestire la natura continua delle grandezze fisiche reali impone che
informazioni continue come i profili di drogaggio siano rappresentate sulla griglia
mediante un numero discreto di nodi, che quindi sono definite unicamente per
un numero finito di punti nel dominio spaziale.
29
Strumenti di simulazione
Figura 21: Gerarchia di utilizzo dei File
Sentaurus Device riceve in input un file con estensione des.cmd in cui sono contenute,
sotto forma di un particolare linguaggio, tutte le informazioni riguardanti la struttura
analizzata, le condizioni di analisi, il tipo di simulazione, l'output da generare e molto
altro. Il file di input è diviso in varie sezioni: File {}, Electrode {}, Physics {}, Plot {},
Math {} e Solve {}. Qualora si stiano effettuando simulazioni di tipo mixed mode è
necessario inserire due sezioni aggiuntive, denominate Device {} e System {}. Risulta
difatti di particolare interesse il supporto per le simulazioni in modalità mista ,mixed
mode, in quanto permette l'analisi del dispositivo assieme al circuito che lo contiene[8]. Il
fatto di possedere una vasta libreria di modelli permette a Sentaurus Device di eseguire:
1. simulazioni su singolo dispositivo (dispositivo descritto dal file di mesh);
2. simulazioni su dispositivo singolo e circuito descritto mediante netlist SPICE
3. simulazioni su dispositivi multipli connessi con circuiteria descritta mediante
netlist SPICE.
In questo particolare caso, oltre all'insieme di equazioni dato, saranno presenti anche delle
altre che legano reciprocamente i dispositivi.
Le principali tipologie di simulazioni che si possono eseguire, sono due: QuasiStazionaria e Tempo-Variante. Si riporta di seguito, una breve descrizione di ogni sezione
del file des.cmd e le relative informazioni da inserire in ognuna di esse, rinviando a [1]
per maggiori dettagli.
30
Strumenti di simulazione
Il file dei comandi
Il file di comandi per il simulatore è organizzato in diverse sezioni, ciascuna delle quali
descrive un ben definito aspetto della simulazione da eseguire. L’ordine con il quale sono
inserite le sezioni non è rilevante: è buona regola però strutturare il file in modo che
risulti ben organizzato concettualmente, inserendo ad esempio prima la sezione che
definisce i parametri matematici e fisici rispetto quella che definisce le soluzioni da far
calcolare al simulatore, così che risulti anche più leggibile[7].
Sezione File:
questa sezione specifica i nomi dei file di ingresso che contengono l’informazione
riguardo alla struttura del dispositivo ed i parametri fisici da utilizzare e quelli di uscita
che andranno a contenere i valori delle grandezze elettriche calcolate.
Input Files: un dispositivo può essere descritto mediante un unico file con estensione
.tdr, che contiene informazioni riguardo la geometria della struttura, le regioni, i
materiali, la posizione dei contatti, i punti della mesh che la caratterizzano ed anche i
profili di drogaggio. Nel formato DF-ISE, invece, il software necessita di due file in
input, uno di griglia .grd ed uno di doping .dat ed insieme contengono le medesime
informazioni del file in formato .tdr. Può essere anche indicato un file di estensione .par,
in cui sono specificati ulteriori parametri opzionali.
Output Files: uno dei file in output alla simulazione è denominato Current, ha
estensione des.plt e memorizza i risultati riguardanti le grandezze macroscopiche quali
corrente, tensione, e carica in corrispondenza di ciascuno dei contatti e, nelle simulazioni
31
Strumenti di simulazione
transitorie, il tempo. Poi vi è un file denominato Plot con estensione des.tdr o des.dat, a
seconda che in input ci sia un file di griglia in formato .tdr o .grd e contiene i dati fisici
del dispositivo in termini di grandezze elettriche microscopiche, come ad esempio densità
di elettroni (e/o lacune), intensità del campo elettrico, potenziale. Un file avente
estensione des.log viene creato automaticamente all'avvio di Sentau rus TCAD e tiene
memoria di tutti i dati calcolati durante la simulazione, inclusi i modelli fisici utilizzati, i
valori dei paramenti considerati o gli eventuali messaggi di errore. I file di uscita saranno
interpretati dai software INSPECT e TECPLOT, il primo si occupa di graficare le
grandezze macroscopiche mentre il secondo quelle microscopiche.
Sezione Electrode: qui si definiscono tutti i contatti elettrici del dispositivo da
simulare.
Ogni contatto non menzionato in questa sezione, verrà ignorato da Sentaurus Device. Per
il corretto funzionamento della simulazione è necessario che il nome qui riportato,
coincida esattamente con quello assegnato al contatto, durante la fase di creazione della
struttura. Oltre al nome devono essere definite le condizioni iniziali di polarizzazione,
come la tensione in Volt e altre specifiche opzionali. Infatti di default esso è considerato
ohmico, ma si può definire se sia di tipo resistivo, floating, Schottky o altro.
3.Thermode: è molto simile alla sezione appena trattata, la differenza è che consente di
descrivere eventuali contatti dal punto di vista della temperatura che assumono,
specificandola come condizione iniziale, assieme al nome del contatto stesso. Per il
seguente lavoro di tesi, tale sezione, non è stata contemplata.
4. Physics: permette di selezionare i modelli fisici da utilizzare nella simulazione, di
definire le proprietà fisiche e le eventuali condizioni di simulazione del dispositivo.
32
Strumenti di simulazione
I modelli fisici possono essere specificati globalmente in tutta la struttura, oppure
limitatamente a regioni o materiali.
Tra i vari modelli a disposizione, si può scegliere di impostare:
- i livelli quasi-Fermi: la densità di elettroni e lacune può essere calcolata a partire dal
potenziale quasi-Fermi delle cariche stesse, usando ben note formulazioni.
Sentaurus Device utilizza uno schema di approssimazione per determinare il valore
costante del potenziale quasi-Fermi.
- la statistica di Fermi-Dirac: viene utilizzata per modellare la statistica di occupazione
dei livelli energetici, in situazioni di fuori equilibrio, sostituendo la statistica di
Boltzmann.
- equazioni di trasporto: scegliendo se basarsi sul modello della Drift Diffusion, sul
modello Termodinamico o Idrodinamico.
- modelli di mobilità: tengono conto anche della degradazione della mobilità dei portatori,
dovuta a vari fattori, come l'alta concentrazione di drogante, il raggiungimento della
velocità di saturazione a causa del campo elevato, alla dipendenza dal campo trasverso.
- modelli di generazione e ricombinazione: il modello di ricombinazione usato
normalmente e quello di Shockley-Read-Hall (SRH) in cui tale fenomeno dipende per
gran parte dall' introduzione di livelli energetici intermedi, posti all'interno dell'energygap e presenti a causa delle imperfezioni nel reticolo.
- modelli di generazione ottica: sono disponibili modelli che simulano la generazione
ottica dovuta all'irraggiamento del dispositivo.
33
Strumenti di simulazione
- modello a bande: e possibile selezionare il modello a bande più opportuno, impostando
dei parametri come band-gap, affinità elettronica, ma anche le densità intrinseche e le
masse effettive di elettroni e lacune.
- boundary conditions: possono essere specificate particolari condizioni al contorno, sia
dal punto di vista elettrico (condizioni sui contatti), che termico. Sentaurus Device
applicherà un modello di parametri appropriato per ogni condizione specificata
.
- velocità di saturazione per elettroni e lacune.
- rumore: esistono modelli che consentono di tenere conto delle non idealità statistiche
del dispositivo e di simulare così, in maniera più adeguata possibile, le variazioni
statistiche dei portatori.
5. Device {} e System {}: Tali sezioni sono presenti solamente nelle simulazioni in
modalità mixed-mode. La prima serve per specificare tutti i dispositivi coinvolti nella
simulazione, mentre la seconda, consente di descrivere le connessioni circuitali tra i
dispositivi stessi, mediante sintassi SPICE.
6. Plot{}: in questa sezione si specificano quali dati dovranno essere salvati nei file di
uscita, per poter poi essere visualizzati.
Sono disponibili una grande quantità di grandezze visualizzabili e graficabili, sia
macroscopiche, come correnti, tensioni ai nodi, ma anche microscopiche, come il valore
del campo elettrico, la densità di cariche in un certo punto, il tasso di ricombinazione.
34
Strumenti di simulazione
Ovviamente maggiore è il numero di dati salvati e maggiore sarà l'accuratezza con cui si
descriverà il comportamento di un particolare dispositivo, ma anche maggiore sarà il
costo computazionale della simulazione.
7. Math{}: Il simulatore risolve le equazioni del dispositivo, costituite essenzialmente da
un insieme di equazioni alle derivate parziali auto-consistente, tramite un meccanismo
iterativo sulla griglia discreta.
Per ogni iterazione un errore è calcolato e Sentaurus Device cerca di convergere ad una
soluzione caratterizzata da un errore piccolo a sufficienza. In questa sezione è possibile
definire alcuni parametri relativi al solutore matematico utilizzato, quale il numero
massimo di iterazioni, l’errore massimo commesso al passo n-esimo, ecc.
Le due principali tipologie di istruzioni sono:
1. Device Specific: si riferiscono a parametri che riguardano i metodi di risoluzione
del singolo dispositivo;
2. Global Specific: riguardano una serie di parametri globali che devono essere presi
come riferimento nei processi di risoluzione dell'intero sistema, a prescindere
dalle caratteristiche di ogni singolo dispositivo.
8. Solve{}: La sezione Solve è l’unica all’interno del file di comando in cui l’ordine in cui
sono scritti i comandi e la loro gerarchia `e importante.
35
Strumenti di simulazione
Essa è composta da una serie di comandi che indicano come deve essere eseguita la
simulazione e che sono attivati rigorosamente secondo la sequenza con la quale sono
elencati.
I comandi di simulazione sono generalmente chiavi di alto livello che prevedono un
ulteriore numero di comandi di basso livello come parametri. Un semplice esempio di una
serie di comandi di simulazione è riportato qui di seguito:
Con il comando Poisson imponiamo che come primo passo di calcolo venga risolta la
sola equazione di Poisson nel dispositivo[7]. La soluzione così ottenuta è poi utilizzata
come punto di partenza per il calcolo della soluzione del passo successivo: in questo caso
si tratta del sistema formato dall’equazione di Poisson e dalle due equazioni di continuità
degli elettroni e delle lacune. Il comando Coupled agisce infatti attivando il solutore non
lineare basato sul metodo di Newton che va a risolvere il sistema di equazioni specificate
come parametri. Il comando Plot permette di effettuare il salvataggio della soluzione
calcolata fino a quel momento. Le variabili salvate saranno quelle specificate nella
sezione Plot del file di comando.
L’operazione successiva richiesta al simulatore è il calcolo di una nuova soluzione,
partendo da quella calcolata fino a questo punto, attraverso la variazione delle condizioni
al contorno del dispositivo. Il comando Quasistationary agisce sulle variabili agli elettrodi
(tensione, corrente, temperatura o sorgente di calore) e le modifica gradualmente
seguendo una rampa specificata con i parametri opzionali. Il comando Quasistationary va
richiamato quando il dispositivo è già stato risolto. La simulazione viene eseguita reiterando tra le variazioni delle condizioni al contorno e risolvendo ad ogni passo le
equazioni specificate nel dispositivo. Nel caso dell’esempio viene applicata all’elettrodo
’P’ una rampa di tensione con valore finale pari a 100V; l’ampiezza massima di una
36
Strumenti di simulazione
singolo step è fissata in 0.01×(100 V) = 1V, l’ampiezza minima in 1·10-7×(100 V) =
1·10-5 V. L’ampiezza di ogni step è calcolata dinamicamente dal simulatore all’interno di
questi due parametri in relazione alla difficoltà con la quale nei passaggi precedenti si è
ottenuta la convergenza. Il valore iniziale dello step è fissato in 1 x10-4 x(100 V) = 10mV.
All’interno di un comando Quasistationary è possibile attivare il salvataggio periodico
della soluzione lungo la rampa inserendo un comando Plot, in cui è possibile specificare
il numero di salvataggi da effettuare (intervals=30).
Figura 22: schema di risoluzione per simulazioni Quasi-Stazionarie
Se invece si intende lavorare in modalità Tempo-Variante, si deve stabilire innanzitutto a
quale intervallo o intervalli di tempo estendere la simulazione ed i relativi passi di
incremento voluti. Infatti Sentaurus Device consente la simulazione di transitori, ovvero
risolve le equazioni date, in funzione di step temporali.
Figura 23: Schema di risoluzione per simulazioni Tempo-Varianti
Vi è inoltre la possibilità di annidare tra loro simulazioni ed effettuare comandi di Plot
parziali in concomitanza di precisi istanti di tempo o di particolari condizioni. Nel caso in
cui la simulazione dipenda da un'altra precedentemente effettuata, è sufficiente inserire il
relativo file .sav all'interno della presente sezione, poiché tale file contiene tutte le
informazioni necessarie al restart della simulazione.
Diversamente da tutte le altre sezioni, qui è molto importante l'ordine gerarchico in cui i
comandi vengono immessi, in quanto vengono eseguiti in modo rigorosamente
sequenziale. Il comando Coupled consente di risolvere mediante l'algoritmo iterativo di
37
Strumenti di simulazione
Newton più equazioni nella stessa simulazione. I possibili parametri del comando sono il
numero massimo di iterazioni permesse, la precisione desiderata della soluzione, il
risolutore lineare da utilizzare e se alla soluzione è consentito peggiorare nel corso di un
certo numero di iterazioni.
Generazione Ottica
La caratterizzazione del fascio laser incidente il fotodiodo è una fase molto importante nel
progetto considerato, quindi necessita di un particolare riguardo[7].
Il meccanismo alla base della generazione ottica è il seguente: un flusso di particelle
(fotoni) incide la superficie di un dispositivo, viene assorbita e come conseguenza
vengono prodotte coppie elettrone-lacuna, che vanno a contribuire alla corrente in modo
proporzionale all'irraggiamento luminoso ricevuto. In questo modo, è sufficiente misurare
la corrente o la tensione ai capi del dispositivo, per ottenere una stima della carica
generata a seguito dell'illuminazione. Sentaurus Device contempla vari modelli utili per il
calcolo del tasso di generazione ottica, e nel particolare caso in esame è stato applicato, il
metodo Optical Beam Absorption, in quanto permette di modellare con facilità la
generazione ottica, partendo dal semplice assorbimento di fotoni. Si possono specificare
all'interno della stessa simulazione un numero qualsiasi di fasci, ad esempio con diverse
lunghezze d'onda; inoltre, la generazione ottica, può essere limitata all'interno di un
particolare materiale o di una regione del dispositivo considerato.
La dichiarazione del modello deve essere effettuata all'interno della sezione Physics {} ed
un esempio è il seguente:
38
Strumenti di simulazione
in cui :
- WaveLength, specifica la lunghezza d'onda del fascio luminoso incidente,
- WavePower, indica la potenza dell'onda incidente,
- SemAbs, specifica il modello di assorbimento usato e RSS è proprio il modello di
assorbimento del silicio;
- SemSurf, permette di definire la coordinata lungo l'asse z, che individua la
superficie del semiconduttore, che verrà irraggiata dal fascio ottico,
- SemWindow, indica le coordinate lungo l'asse x e y, che delimitano la finestra di
incidenza del laser;
- WaveTime, rappresenta l'intervallo di tempo durante il quale l'intensità del fascio
incidente rimane costante,
- WaveXYsigma, è la deviazione standard del decadimento gaussiano del fascio, al
di fuori della finestra,
- WaveTsigma, è la deviazione standard del decadimento gaussiano del fascio, al di
fuori dell'intervallo di tempo specificato.
- WaveLength può essere sostituito con WaveEnergy a seconda che si voglia
descrivere la radiazione incidente, in termini di lunghezza d'onda o energia in eV,
posseduta dai fotoni.
Il fascio ottico incidente è modellato da una distribuzione Gaussiana e, di conseguenza, è
caratterizzato fondamentalmente da tre parametri: il valore medio, ovvero il punto di
incidenza che coincide con il punto in cui è centrata la finestra, il decadimento nel tempo
e nello spazio.
Figura 24: procedura RecBoxInteger
Per visualizzare graficamente gli effetti della generazione ottica, è necessario inserire
nella sezione Plot{} la parola chiave OptBeam. Mentre per attivare il calcolo di
generazione ottica inserire nella sezione Math{} il comando RecBoxInteger, che
garantisce anche una miglior accuratezza del risultato. Infatti se l'intensità del fascio varia
rapidamente nello spazio, la precisione del calcolo dell'intensità stessa risulta bassa,
specialmente se vengono utilizzate mesh grossolane della struttura e non vengono prese
particolari precauzioni. Per risolvere questi problemi, si integra la distribuzione del
39
Strumenti di simulazione
fascio, su di un poligono ad ogni nodo della mesh, ne è associato uno. Il poligono
(Control Volume) viene suddiviso in tanti piccoli parallelepipedi (RexBox) e
l'integrazione analitica viene effettuata su queste suddivisioni.
Si possono specificare anche tre parametri addizionali:
RecBoxInteger({Epsilon}{MaxNumberOfLevels}{MaxNumberOfBoxes})
Il primo indica la massima deviazione relativa del volume suddiviso in celle, rispetto ogni
singola il numero massimo di suddivisioni utilizzate per approssimare ogni poligono. Se
tali parametri non vengono esplicitati, si considerano di default pari a (1e-2 10 1000).
Ovviamente nelle strutture 2D, il poligono sarà una struttura bidimensionale e i
parallelepipedi dei semplici rettangoli.
Calcolo della generazione ottica
E stato utilizzato il modello Optical Beam Absorption che calcola la generazione ottica,
partendo dal semplice assorbimento di fotoni e si basa sulla legge di Beer, una relazione
empirica che lega la quantità di luce assorbita da un mezzo alla natura chimica, alla
concentrazione ed allo spessore del mezzo attraversato.
Nella figura sottostante si illustra un fascio ottico che incide su un dispositivo 3D[7].
Figura 25: Fascio incidente il dispositivo
J0 indica il numero di fotoni che attraversano un area di 1cm2 in 1s, in corrispondenza del
centro della finestra del semiconduttore, (xmin; ymin) e (xmax; ymax) definiscono la
finestra del semiconduttore (Semiconductor Window), sigma xy è la deviazione standard
della distribuzione spaziale Gaussiana, che descrive il decadimento del'intensità del fascio
ottico al di fuori della finestra del semiconduttore. V è la velocità della finestra
40
Strumenti di simulazione
perpendicolare alla direzione del fascio incidente (fraccms). Quella che è stata chiamata
finestra del semiconduttore (Semiconductor Window) è una porzione rettangolare di
dimensioni (xmin; ymin)x(xmax; ymax) della superficie del dispositivo, su cui viene
indirizzata tutta la stimolazione luminosa incidente. La forma, Fxyv, che assume nello
spazio il fascio incidente, è definita dalla dimensione della Semiconductor Window, dal
suo decadimento Gaussiano nello spazio e la sua velocità. In tal modo Fxyv, è pari a 1
all'interno della finestra del semiconduttore e decresce a zero con andamento Gaussiano,
al di fuori della finestra.
Le relazioni utili a descrivere il problema di foto-generazione sono le seguenti:
E ph =
hc
J0 =
in cui:
-
λ
[µm]
P0
E ph
P0 indica la potenza dell'onda incidente [ W/cm2 ],
µe la lughezza d'onda [cm],
h µe la costante di Planck [Js],
c µe la velocitµa della luce nel vuoto [cm/s ],
Eph è l'energia associata ai fotoni, approssimativamente è pari a
1,24
[eV]
λ[ µm]
Il modello in esame calcola il tasso di generazione ottica lungo l'asse z in base a:
G opt ( z , t ) = J 0 Ft (t )Fxyv • α (λ , z )e
−α • z − z 0
t è la variabile temporale, Ft(t) µe la funzione che descrive il comportamento temporale
del fascio. E’ pari a 1 nell'intervallo di stimolazione [tmin; tmax] e mostra un decadimento
con distribuzione Gaussiana e deviazione standard σt al di fuori di tale intervallo, z0 è la
coordinata della superficie del semiconduttore, α(λ, z) rappresenta la variazione, non
uniforme, del coefficiente di assorbimento lungo l'asse z.
Una formulazione più avanzata è:
G
opt
(z, t ) = J 0 Ft (t )Fxyv • α (λ , z )e
−
z
∫z0 α (λ , z ' )δz '
Inspect
Lo
strumento
software
Inspect
permette
la
visualizzazione,
tramite
grafico
bidimensionale, dell'andamento delle grandezze macroscopiche, quali correnti, tensioni ai
nodi, carica e tempo, calcolate da Sentaurus Device durante la simulazione[8]. Si possono
41
Strumenti di simulazione
ad esempio sovrapporre più grafici sullo stesso sistema di riferimento, permettendo un
rapido confronto delle grandezze ottenute, oppure si possono manipolare a proprio
piacimento le curve, per migliorarne la visibilità, ricorrendo ad un ampio set di funzioni
matematiche tra cui derivazione, integrazione, logaritmo, oppure selezionando una curva
in particolare, si possono visualizzare i dati numerici che la caratterizzano.
Figura 26: Finestra di lavoro di Inspect
Tecplot sv
Tecplot sv è un potente software per la visualizzazione grafica di grandezze
microscopiche, utilizzabile per strutture 2D e 3D.
Grazie all'interfaccia user-friendly, permette di indagare con facilità il comportamento
interno di una struttura, in quanto mostra i risultati delle simulazioni sotto forma di
mappa colorata del dispositivo[8]. E’uno strumento estremamente versatile e con molte
funzionalità, consente infatti di creare animazioni delle simulazioni svolte, sezioni
trasversali del dispositivo, grafici XY ed altro ancora. Inoltre è in grado di graficare anche
le stesse grandezze macroscopiche considerate da Inspect.
Inserendo più comandi di Plot in corrispondenza di diversi istanti temporali all'interno del
file: cmd, in input a Sentaurus Device, nella simulazione Tempo-Variante, è possibile
42
Strumenti di simulazione
risalire al comportamento del dispositivo stimolato in funzione del tempo e Tecplot
riporterà tanti grafici, quanti sono stati gli istanti di tempo specificati. Nella figura si vede
come è distribuito il campo elettrico all’interno di un dispositivo 3D, ottenuta tramite il
tecplot sv.
Figura 27: Esempio di visualizzazione con Tecplot
Il cluster di calcolo INFN GRID
Data l’enorme mole di simulazioni da svolgere si è pensato sin dall’inizio di questo
lavoro di sfruttare le elevate potenzialità che il cluster di calcolo dell’INFN di Perugia
mette a disposizione. Infatti sin dal 2004, con oltre 100 CPU, il cluster dell’INFN di
Perugia offre una potenzialità di calcolo molto elevata diventando uno dei siti INFN
GRID più importanti a livello nazionale[10]. La struttura del cluster di Perugia presenta
vari nodi che possono essere suddivisi nel seguente:
-
UI (User Inteface): ogni gruppo di utenti ha una UI, essa contiene gli account
degli utenti appartenenti al gruppo. Sono gli unici nodi a cui gli utenti possono
accedere;
-
SE (Storage Element): gestisce lo scambio dei dati via GRID, unico per tutto il
cluster;
43
Strumenti di simulazione
-
CE (Computing Element): è l'interfaccia verso la grid e si occupa dello
smistamento dei job, anche questo nodo è unico;
-
WN (Worker Node): sono i nodi che eseguono i job;
-
FS (File Server): sono i nodi che contengono i dati degli esperimenti.
Figura 28: Schema logico del cluster dell'INFN di Perugia
L'utente può accedere alla UI tramite SSH (Secure Shell), da qui può sottomettere job via
GRID o in modo Locale; nel primo caso deve possedere un certificato ed essere iscritto
ad una VO riconosciuta. La sottomissione Locale prevede invece l'utilizzo dei comandi
del batch-system torque
In Figura è riportato una zoom sull’interfaccia da cui l’utente può controllare lo stato di
avanzamento delle simulazioni.
44
Strumenti di simulazione
Figura 29: Stato avanzamento simulazioni
Affinché il pacchetto ISE funziona se correttamente sono stati molti gli accorgimenti
necessari. Si è partiti creando una macchina virtuale, Debian-etch minimale, tramite
tecnologia Xen, su cui è stato installato il software ISE. Questa macchina virtuale è stata
definita server della rete permettendo ai vari nodi del cluster, autenticandosi su essa, di
utilizzare il software ISE.
45
4
Costruzione del fotodiodo
La struttura utilizzata per lo svolgimento del lavoro di tesi è un fotodiodo con dimensione
del substrato di 10x10x10 µm. Per avviare Sentaurus Structure Editor in ambiente Linux,
è necessario digitare nella riga di comando del terminale: - sde Scegliere dalla barra dei
menù File - New per creare un nuovo foglio di lavoro. Nella Material List si può
scegliere il materiale da utilizzare: lasciare come da default il silicio. Dal menù Draw Exact Coordinates per progettare la struttura in funzione delle coordinate spaziali. Infatti
gli oggetti possono anche essere disegnati manualmente, ma nell'ambito di strutture
micrometriche, in cui la precisione di progetto è fondamentale, è consigliabile lavorare in
funzione di specifiche coordinate[8].
Sempre dal menù Draw attivando o disattivando l'opzione Auto Region Naming, si può
scegliere che il programma assegni automaticamente un nome alle varie strutture che si
andranno a creare, o se nominarle in modo autonomo.
Per creare il substrato di silicio Draw - 3D Create Tools - Created Cuboid: disegnare la
forma, trascinando il puntatore e cliccando con il tasto sinistro del mouse sulla finestra
principale, andando a delineare una forma poligonale tridimensionale. A disegno
completato si aprirà una finestra di dialogo Cuboid Definition, nella quale si dovranno
inserire le coordinate spaziali lungo i tre assi di riferimento che definiscono la struttura.
Costruzione del fotodiodo
Figura 30: Tabella di definizione delle dimensioni del diodo
Se la visualizzazione del cubo non risulta ottimale, può facilmente essere modificata
tramite:
Figura 31: Strumenti di visualizzazione custom
Per definire i contatti scegliere dalla barra dei menù Contacts => Contact sets e verrà
visualizzata la seguente finestra:
Figura 32: Tabella di definizione dei contatti
che permette di creare in una sola sessione più contatti; nel caso in questione sono
solamente due: top e substrate.
Per assegnare il nome ai contatti, è sufficiente scriverlo nel campo Contact Name,
lasciando anche inalterati tutti i successivi parametri che sono puramente opzionali.
Premere Set per creare il contatto ( viene così inserito in Defined Contact Sets) e
Activate per renderlo utilizzabile.
47
Costruzione del fotodiodo
Per quanto concerne il posizionamento dei contatti, nel caso delle applicazioni 3D, essi
sono tipicamente collocati sulle facce del dispositivo.
Posizionamento del contatto di substrate:
1. Selezionare substrate dalla lista dei contatti;
2. Selezionare Select Face dalla lista Selection Level;
3. Cliccare l'icona Aperture Select dalla barra degli strumenti;
4. Selezionare la faccia dove verrà posizionato il contatto, che per comodità
corrisponde in questo progetto a quella contenuta nel piano z =10;
5. Contacts => Set face(s) per associare definitivamente il contatto di nome
substrate alla faccia selezionata.
La faccia risulta ora marcata. Il contatto di top, al contrario di quello precedentemente
descritto non occupa un intera faccia dell'oggetto, ma solamente una porzione di essa, per
cui la procedura da seguire risulterà diversa.
Ricordare che le facce coinvolte nel posizionamento dei due contatti sono ai capi opposti
dell'oggetto.
Posizionamento del contatto top:
1. Visualizzare la faccia in cui si dovrà sistemare il contatto metallico (compresa nel
piano z=0);
2. creare un cubetto metallico (scegliere Metal dalla Material List) centrato sulla
faccia del cubo di dimensioni 0.4x0.4 µm:
3. Rimuovere il cubo appena creato, selezionando Select Body dalla lista Selection
Level e premere Canc (o tasto destro del mouse => Delete).
4. Sebbene la regione appena creata sia stata rimossa, ne è comunque rimasta
l'intersezione con la faccia del diodo. Selezionare questa intersezione cliccando
Aperture Select seguito da Select Face e procedere dal passo 1, selezionando
top, anziché substrate.
48
Costruzione del fotodiodo
Figura 33: Tabella di definizione delle dimensioni del contatto metallico
Il passo successivo è definire i profili di drogaggio per la struttura creata.
Sono presenti due tools selezionabili dal menù Device che permettono di definire profili
di drogaggio:
1. uniformi, per drogare uniformemente la struttura (Constant Profile Placement);
2. analitici, quando la diffusione del drogante deve seguire un andamento
descrivibile tramite una funzione analitica.(Analitical Profile Placement).
Il substrato verrà drogato uniformemente con una concentrazione di Boro pari a 1015
atomi cm3 (substrato tipo p) come riportato in figura.
Figura 34: Tabella di definizione dei profili di drogaggio costanti
Si possono selezionare anche limitate regioni della struttura da drogare ed è proprio ciò
che serve per creare una tasca di tipo n sul substrato di tipo p. A tale scopo si seleziona il
49
Costruzione del fotodiodo
menù Mesh => Define Ref/Eval Window => Rectangle per disegnare un rettangolo di
coordinate:
Figura 35: Tabella di definizione delle dimensioni del TOP
A questo punto si può procedere drogando selettivamente questa regione con una
concentrazione di atomi di Fosforo pari a 1019 atomi cm3 che con andamento Gaussiano,
raggiunge una profondità di giunzione pari a 2 µm:
Figura 36: Tabella di definizione dei profili di drogaggio analitici
L'ultimo passo di questo progetto e stabilire un opportuna strategia di mesh, per effettuare
simulazioni accurate della struttura in tempi accettabili. Una proposta è riportata in figura:
50
Costruzione del fotodiodo
Figura 37: Tabella di definizione delle proprietà della Mesh
Cosi siamo riusciti a costruire il fotodiodo, in 3D, che riportiamo nel seguito. Il
successivo passo sarà quello della scelta della mesh.
Figura 38: 3D del fotodiodo
51
Costruzione del fotodiodo
Generazione della Mesh
Per generare la mesh è necessario prima di tutto salvare il lavoro svolto finora File - Save
Model e successivamente Mesh - Build Mesh, inserire in alto lo stesso nome con cui si è
salvata la struttura e premere Build Mesh:
Figura 39: Tabella di definizione dei motori di generazione della mesh
Per scegliere la Mesh giusta per il dispositivo in simulazione è importante conoscere i tre
motori di generazione della mesh[9]. Il generatore della mesh è un insieme di strumenti
che produce mesh a elementi finiti che si possono applicare nelle simulazioni di
dispositivi a semiconduttore, nelle simulazioni di processi e di campi elettromagnetici.
Cosi vengono generate delle discretizzazioni spaziali di alta qualità per i dispositivi in
1D, 2D e anche in 3D.
Lo strumento di generazione della mesh è composto di tre motori di generazione :
1. Sentaurus Mesh: è un generatore robusto in grado di produrre delle mesh per le
strutture simmetriche allineate agli assi in 2D e in 3D. Inoltre il Sentaurus Mesh
contiene un set di strumenti in grado di generare mesh appropriate per mettere in
evidenza gli effetti di bordo.
52
Costruzione del fotodiodo
Questo generatore è consigliato per le strutture perfettamente simmetriche in
quanto in questo modo è più facile controllare le zone critiche di variazione del
drogaggio.
Esso contiene 2 tipi di generatori di mesh:
a. axis-aligned che si utilizza molto frequentemente nel Sentaurus Device e
Sentaurus Process.
b. tensor-product si usa nei casi in cui si ha a che fare con delle simulazioni di
campi elettromagnetici nel Sentaurus Device Elettromagnetic Wave
solver(EMW).
2. Noffset3D: è un generatore di mesh avanzato che produce delle mesh triangolari
in 2D e tetrahedrali in 3D. Le mesh prodotte da Noffset3D possono contenere
strati di elementi che sono quasi paralleli alle superfici date delle strutture dei
dispositivi a semiconduttore. Questo generatore è consigliato per le strutture
come i MOS che rappresentano delle geometrie non allineate agli assi, con delle
superfici curve o irregolari
3. Mesh: è un generatore per le strutture allineate agli assi in grado di produrre
mesh a elementi misti in 1D, 2D e 3D. Questo generatore è consigliato per le
strutture a una sola dimensione 1D.
La scelta di uno dei generatori dipende fortemente dalla geometria della struttura da
simulare.
In questo lavoro di tesi è stato utilizzato il generatore Sentaurus Mesh (SnMesh) nella
versione axis-aligned.
Figura 40: 3D del fotodiodo con Mesh generata da un generatore di tipo Mesh
53
Costruzione del fotodiodo
Nella figura 39 viene mostrato il 3D di un fotodiodo utilizzando il generatore Mesh. Si
nota che ci sono delle asimmetrie le quali non possono essere spiegate da nessuna delle
proprietà del dispositivo costruito, in quanto esso è perfettamente simmetrico. Questa
asimmetria è dovuta al fatto che il generatore di tipo Mesh, non è appropriato alla
geometria che rappresenta questa struttura. Infatti questo problema si risolve utilizzando
l’altro generatore di mesh, di nome Sentaurus Mesh (SnMesh), attraverso il quale è stata
ottenuto la mesh della figura seguente che come si vede è perfettamente simmetrica.
Figura 41: 3D del fotodiodo con Mesh generata da un generatore di tipo Axis Aligned
Applicando questa nuova mesh, si guadagna in termini di tempi di simulazione. Questo
perché la nuova mesh generata con il generatore SNMesh, è costruita sulla base di un
algoritmo più semplice il quale utilizza soltanto dei quadrati e triangoli. Il numero dei
punti della mesh aumenta, ma il tempo di simulazione per lo stesso numero di punti, è
minore.
54
5
Simulazioni
Simulando la struttura appena creata abbiamo la possibilità di descrivere il
comportamento del dispositivo, quando sottoposto ad irraggiamento da parte di un
fascio laser, sia misurando le grandezze macroscopiche che microscopiche, che lo
caratterizzano. Lo scopo è quello di ottenere previsioni, quanto più accurate
possibili, riguardo tale comportamento e riguardo la funzionalità del dispositivo.
Per questo motivo si fanno variare parametri tecnologici, parametri di simulazione
e di stimolo, al fine di visualizzare la reazione del dispositivo e selezionare la
migliore condizione di funzionamento. Le simulazioni le possiamo dividere in 2
grandi gruppi:
1. Simulazioni Steady-State
In questo gruppo possiamo far variare i parametri tecnologici del diodo, ovvero:
a) Doping substrato
b) Doping well
c) Profondità di giunzione
d) Profondità del diodo
e) Dimensione del contatto ecc.
Oppure i parametri di struttura/simulazione come:
Simulazioni
a) Effetti di griglia
b) Effetti di bordo ecc.
2. TV-Simulazione ottica
In questo caso i parametri che si possono variare sono dei parametri che non hanno più a
che fare con il dispositivo progettato ma con le proprietà del fascio ottico che incide il
fotodiodo, come :
a) Lunghezza d’onda
b) Potenza del fascio
c) Punto di incidenza ecc.
Sono state considerate tre differenti lunghezze d'onda da associare al fascio laser. I colori
scelti per distinguerle non rispecchiano la reale colorazione della radiazione, ma sono
solo una convenzione che verrà adottata in questa trattazione per facilitare la
visualizzazione dei risultati, come anche l'appartenenza ad una precisa area dello spettro
elettromagnetico.
1060 nm - infrarosso ;
783 nm - visibile ;
407 nm - ultravioletto.
Il fascio laser è stato diretto in modo tale da incidere sempre la finestra centrale del
dispositivo, poiché è l'unica contenuta interamente nell'area della n-well (in rosso in
figura) e la durata dell'impulso laser è pari a 50 ps, a partire dall'istante 8.0 e^6 s.
Figura 42: Finestre di incidenza del fascio laser
Le simulazioni eseguite sono divisi in tre grandi gruppi facendo riferimento alle tre
lunghezze d'onda sopra elencate, variando parametri tecnologici, di simulazione e di
56
Simulazioni
stimolo della struttura. Risulta interessante, così, studiare la reazione del dispositivo a tali
variazioni e a utilizzare i risultati ottenuti per renderlo più efficiente. E’ importante
sottolineare che le simulazioni in cui si sono fatti variare i parametri tecnologici e di
simulazione, sono state eseguite con le medesime condizioni sullo stimolo, ovvero la
stessa potenza, direzione e posizione d'incidenza.
L'analisi dei risultati si basa sulla misurazione della differenza di potenziale (DV ) ai capi
della struttura, inizialmente polarizzata alla tensione di 1.7 V.
Per comprendere appieno tale procedura di misura, bisogna aver ben presente lo schema
circuitale di un pixel APS ed il suo funzionamento.
In tutte le simulazioni di cui di seguito si riportano i risultati, quando si parla di differenza
di potenziale, ed è proprio su questo valore che si basano i confronti tra le varie strutture
simulate e al variare dei diversi parametri.
Simulazione Quasi-Stazionaria (QS)
Nei primi istanti di simulazione, il reset carica il fotodiodo come fosse una capacità,
partendo dalla tensione 1.7V (tensione di polarizzazione) fino alla tensione 1.8V. In
questa condizione il reset è quindi alto ed il diodo risulta insensibile ad eventuali
radiazioni incidenti. La parte appena descritta viene descritta nella cosiddetta simulazione
Quasi-Stazionaria (QS), in cui la tensione di uscita del fotodiodo varia seguendo il
segnale di reset.
Caratteristica I-V del diodo
E’ di particolare interesse vedere come varia la cosiddetta caratteristica( i,v) del diodo al
variare dei parametri tecnologici e dei parametri di struttura e simulazione in modalità
Steady-State(Stato stazionario). Si riporta come riferimento una caratteristica:
57
Simulazioni
Figura 43: Caratteristica del diodo
La parte sinistra del grafico rappresenta il comportamento del diodo in polarizzazione
inversa. Abbiamo detto, a proposito della giunzione pn, che in polarizzazione inversa essa
non conduce[1]. Notiamo, invece, dal grafico che una corrente interessa il diodo anche se
piccolissima, dell’ordine dei microampere o addirittura nanoampere. La presenza di tale
corrente si spiega ricordando che nella giunzione pn sono presenti portatori di carica
minoritari. Nella zona p abbiamo una gran quantità di lacune introdotte con il drogaggio
ma ciò non toglie che esista una piccola quantità di elettroni che abbandonano
naturalmente gli orbitali degli atomi di silicio. Essi sono i portatori minoritari nella zona
p. Analogamente troviamo una piccola quantità di lacune nella zona n. Se il diodo è
polarizzato inversamente, abbiamo un campo elettrico che va dalla zona n alla zona p. Le
lacune non possono passare dalla zona p alla zona n e gli elettroni non possono più
passare dalla zona n alla zona p. I portatori di carica minoritari possono invece
attraversare la giunzione perché trovano un campo elettrico favorevole. Gli elettroni
minoritari che si trovano nella zona p, vengono spinti, infatti, in direzione opposta al
campo elettrico, cioè verso la zona n e le lacune minoritarie che si trovano nella zona n
vengono spinte nella direzione del campo elettrico cioè verso la zona p. La corrente di
cariche minoritarie è quella rappresentata nella caratteristica e prende il nome di corrente
di saturazione inversa.
I seguenti grafici sono ottenuti utilizzando lo strumento Inspect, del pachetto Sentaurus
TCAD, il quale è in grado di elaborare i file prodotti durante le simulazioni.
Vediamo per prima l’effeto della variazione del drogaggio di substrato, sulla caratteristica
i-v del diodo.
58
Simulazioni
Variazione del drogaggio di substrato :
Variando il drogaggio si ottengono le seguenti curve:
Figura 44: Variazione del drogaggio del well
.
Figura 45:
Una fondamentale relazione relativa alla regione di carica spaziale (brevemente RCS), si
ricava facendo considerazioni sul valore massimo del campo elettrico all’interno della
regione stessa. Si trova infatti che:
Na × X p = Nd × X n
59
Simulazioni
Questa relazione dice che l’estensione della RCS varia in maniera inversamente
proporzionale alla concentrazione di drogante. Quanto più la concentrazione di drogante è
elevata, tanto meno estesa è la RCS. La RCS si estende prevalentemente nella regione
meno drogata.
Si nota quindi, che per un drogaggio maggiore del substrato o del well è maggiore la
corrente che attraversa il diodo. Questo perché maggiore è il drogaggio maggiore è il
tasso di ricombinazione e quindi un substrato molto drogato diventa meno resistivo.
Figura 46: Variazione della profondità di giunzione
60
Simulazioni
Simulazione Tempo-Variante(TV)
La simulazione Tempo-Variante (TV) inizia quando il reset portandosi al valore basso,
rende il fotodiodo suscettibile alla radiazione incidente ed è proprio sotto questa
condizione che viene irraggiato da uno stimolo laser all'istante 8.0e06 s. Come risposta, si
assiste ad un improvviso abbassamento della tensione in corrispondenza del catodo del
fotodiodo, causata dalla generazione di carica libera dovuta all'assorbimento di fotoni.
Influenza della lunghezza d’onda
La radiazione infrarossa è caratterizzata da lunghezze d'onda molto maggiori rispetto a
quelle del visibile e dell'ultravioletto. Per questo motivo penetra con più facilità la
struttura, riuscendo anche ad oltrepassarla, mentre la radiazione visibile, e ancora di più
quella ultravioletta, interessano solamente gli strati più superficiali del dispositivo.
Alla luce di quanto detto, ci si aspetta che le prove effettuate alla lunghezza d'onda di
1060 nm risentano poco delle variazioni riguardanti i livelli superficiali del dispositivo, al
contrario di quelle effettuate a 783 nm e 407 nm che a seconda di quanto penetrano la
superficie, più o meno in vicinanza della n-well, ne risentiranno maggiormente.
Analisi con Inspect
Di seguito si riporta il risultato delle simulazioni svolte in corrispondenza delle tre
lunghezze d’onda utilizzate durante le simulazioni.
61
Simulazioni
Figura 47: Caduta di tensione in funzione della lunghezza d'onda della radiazione incidente e
del tempo
Quando un fascio ottico incide il dispositivo può penetrare più o meno in profondità la
struttura dando luogo a vari comportamenti: il fascio ottico ha una lunghezza d'onda
elevata, per cui riesce ad oltrepassare la struttura (il silicio risulta trasparente), generando
una caduta di potenziale piuttosto piccola, in genere dell'ordine dei mV(questo è il caso
della lunghezza d’onda di 1060nm); il fascio ottico presenta una lunghezza d'onda molto
corta per cui non riesce a penetrare gli stati della struttura e la generazione ottica rimane
estremamente superficiale non riuscendo così a giungere alla regione attiva del
dispositivo. Anche in questo caso la caduta di potenziale misurata in uscita al fotodiodo e
piccola (questo è il caso della lunghezza d’onda di 407nm). Alla fine se il fascio ottico ha
una lunghezza d'onda opportuna, tale da riuscire a penetrare la struttura sufficientemente
da raggiungere la giunzione di raccolta, ma non troppo da oltrepassarla. Questa è la
lunghezza d'onda rispetto cui si misura la massima caduta di potenziale e che assicura la
massima raccolta di carica.(caso della lunghezza d’onda di 783nm).
Analisi con Tecplot
62
Simulazioni
Figura 48: 1) 1060nm 2)783nm 3)407nm
Queste figure sono state ottenute mediante il software Tecplot, che consente di
visualizzare la reazione del dispositivo allo stimolo laser in ingresso, fornendo
informazioni sulle grandezze microscopiche che caratterizzano il suo comportamento
interno.
Le immagini , sono come delle fotografie scattate nell'istante 8.00001e6 s, ovvero 10 ps
dopo che l'impulso laser è stato inviato contro la superficie della struttura e non si è
ancora esaurito, poiché ha una durata di 50 ps.
Considerata una grandezza microscopica, si confronta come varia in funzione della
lunghezza d'onda della radiazione incidente.
Si osserva che l'intensità di generazione ottica all'aumentare della lunghezza d'onda della
radiazione cala, ma allo stesso tempo riesce a raggiungere strati più profondi del
substrato.
Una grandezza microscopica legata alla generazione ottica è la densità di elettroni, 783
nm è la lunghezza d'onda in corrispondenza di cui si ha una densità di elettroni, al livello
di substrato, più elevata. Relativamente a 1060 nm, dal momento che la generazione
ottica corrispondente a tale lunghezza d'onda è di due ordini di grandezza minore della
precedente, anche la densità di elettroni sarà più bassa. Dato che il fascio ottico avente
lunghezza d'onda pari a 407 nm rimane molto superficiale e gli elettroni si ricombinano
nelle prime frazioni di µm della struttura, non vanno a contribuire alla densità di elettroni
nel substrato, che quindi risulta molto inferiore rispetto ai due casi appena trattati. Lo
63
Simulazioni
studio di queste figure risulta utile per descrivere le immagini riguardanti la
ricombinazione. Infatti la densità di elettroni, a tutte le lunghezze d'onda, è massima nella
regione attiva del dispositivo e proprio lì si ha il maggior tasso di ricombinazione, che poi
va scemando lungo la direzione di incidenza del fascio laser. Le immagini relative a 1060
nm e 783 nm, mostrano lo stesso tasso di ricombinazione nella regione attiva, mentre a
livello di substrato per le osservazioni fatte, il tasso risulta più elevato per la lunghezza
d'onda 783 nm.
Figura 49: Densità di elettroni 1) 1060nm 2) 783nm 3) 407nm
64
Simulazioni
Figura 50: Ricombinazione SRH 1) 1060nm 2) 783nm 3) 407nm
Invece il campo elettrico ed il potenziale elettrostatico, come è logico che sia, non variano
al variare della lunghezza d'onda.
Figura 51: Campo Elettrico 1) 1060nm 2) 783nm 3) 407nm
65
Simulazioni
Figura 52: Potenziale Elettrostatico 1) 1060nm 2) 783nm 3) 407nm
Variazione del drogaggio di substrato
Utilizzando sempre gli stessi parametri della struttura del dispositivo, sono state eseguite
delle simulazioni facendo variare soltanto i valori del drogaggio di substrato. Ricordando
che il valore standard utilizzato è 1015 atomi/cm3, gli altri sono 1014 atomi/cm3, 1016
atomi/cm3 e 1017 atomi/cm3.
Analisi con Inspect
Vediamo le varie cadute di potenziale in funzione del tempo per le tre lunghezze d’onda
facendo quindi variare il drogaggio del substrato:
66
Simulazioni
Figura 53: 1060nm
Figura 54: 783nm
67
Simulazioni
Figura 55: 407nm
Come ci aspettavamo le più grandi cadute di potenziale si verificano per la lunghezza di
783nm, che come detto è una lunghezza
tale da riuscire a penetrare la struttura
sufficientemente da raggiungere la giunzione di raccolta, ma non troppo da oltrepassarla.
Poi una caduta di potenziale minore per la lunghezza di 407nm e infine le più piccole
cadute di potenziale si vedono per la lunghezza di 1060nm. Nello specifico per tutte le
lunghezze d’onda si nota un andamento decrescente della caduta di tensione
all’aumentare della concentrazione dell’ drogaggio di substrato. Questo comporta una
minore raccolta di carica con conseguente riduzione della caduta di potenziale. Inoltre un
substrato poco drogato diventa più
resistivo e la caduta di potenziale ai suoi capi
aumenta. Alla frequenza dell'infrarosso è meno evidente, in quanto le cadute di tensione
sono dell'ordine del mV, invece al visibile e ultravioletto del decimo di Volt.
E’ interessante vedere anche il comportamento del fotodiodo al variare del drogaggio di
substrato da punto di vista delle correnti. Ci aspettiamo un picco di corrente nell’ istante
in cui il fascio ottico incide il fotodiodo, a causa della grande generazione di carica libera
in quel istante temporale(8.0e06 s).
68
Simulazioni
Figura 56: 1060nm
Figura 57: 783nm
69
Simulazioni
Figura 58: 407nm
Per tutte le tre lunghezze d’onda si vede che il picco di corrente è maggiore per il
substrato meno drogato, questo perché come detto prima un substrato poco drogato è più
resistivo e quindi la caduta di potenziale è maggiore e tale sarà anche la corrente prodotta
nel istante di incidenza del fascio ottico.
Analisi con Tecplot
Prendiamo in considerazione il caso di variazione del drogaggio di substrato quando la
lunghezza d’onda del fascio che incide il diodo è di 783 nm (visibile). Come ci
aspettavamo, per una concentrazione piccola del drogante, il substrato risulta più resistivo
e quindi la densità di corrente sarà maggiore in modo da produrre una caduta di
potenziale maggiore ai capi del diodo.
70
Simulazioni
Figura 59: Densità di corrente 1)1014 atomi/cm3 2)1015 atomi/cm3 3)1016 atomi/cm3
4)1017atomi/cm3
Avere basse concentrazioni droganti garantisce alta mobilità delle cariche, un minor tasso
di ricombinazione e di conseguenza agisce positivamente sul tempo di vita dei portatori
minoritari.
Globalmente il campo elettrico risulta più intenso nell'intorno della giunzione e
raggiunge valori di intensità più elevati in corrispondenza del substrato maggiormente
drogato.
71
Simulazioni
Figura 60: Campo Elettrico a)1014 atomi/cm3 b)1015atomi/cm3 c)1016atomi/cm3
d)1017atomi/cm3
Per capire questo risultato bisogna ricordare che la giunzione presenta all’interfaccia una
zona in cui non compaiono le cariche mobili, ma soltanto quelle fisse[1]. Ciò è dovuto
alla ricombinazione (elettroni-lacune) delle cariche mobili che si trovavano a contatto.
Infatti, essendosi verificato un gradiente di concentrazione di cariche, queste hanno
“migrato” ricombinandosi (nasce una corrente di diffusione per la cosiddetta legge di
Fick). Dato lo “svuotamento” di cariche mobili, la zona interessata prende appunto nome
di zona svuotata. Nel resto del materiale questa ricombinazione non è potuta avvenire per
una causa fondamentale che è importante analizzare. Per ogni carica mobile “migrata” è
rimasta nel materiale una carica fissa di segno opposto. La somma di tutte le cariche fisse
(che sono di segno positivo da un lato della giunzione, negativo dall’altro), da luogo ad
un campo elettrico E il quale si oppone a che il fenomeno continui interessando il resto
del materiale e che quindi da luogo ad una barriera. Il campo elettrico E nasce quindi per
costruzione stessa della giunzione, per questo prende nome di campo elettrico di built-in
(ossia di costruzione). Nel caso di un substrato molto drogato le cariche fisse rimaste
dopo la migrazione delle cariche mobili fanno si che il campo elettrico generato sia
minore rispetto a quello generato in un substrato poco drogato.
72
Simulazioni
Variazione del drogaggio di n-well
Lasciando inalterati i parametri del diodo, facciamo variare solo il drogaggio di n-well, da
1019atomi/cm3 a 1018 atomi/cm3 e a 1020 atomi/cm3.
Analisi con Inspect
Vediamo le varie cadute di potenziale in funzione del tempo per le tre lunghezze d’onda
facendo quindi variare il drogaggio del n-well.
Figura 61: 1060nm
Figura 62: 783nm
73
Simulazioni
Figura 63: 407nm
Come si nota anche la variazione del drogaggio del top, ci da risultati simili a quelli di
prima. Più drogato è il contatto di top, meno resistivo è , e quindi la caduta di potenziale
nel istante di incidenza del fascio ottico è minore. La lunghezza d’onda che tale
variazione interessa maggiormente è 783nm(visibile).
Variazione della profondità di giunzione
Un'altra significativa variazione di un parametro tecnologico è quella della profondità di
giunzione.
Lo scopo delle seguenti simulazioni è capire quanto influenza la profondità di giunzione e
quali lunghezze d'onda interessa maggiormente. I valori utilizzati sono:
1µm, 2µm, 3µm.
74
Simulazioni
Figura 64: 1060nm
Figura 65: 783nm
75
Simulazioni
Figura 66: 407nm
Come ci aspettavamo (per quanto detto prima) non ci sono sostanziali cambiamenti per la
radiazione corrispondente alla lunghezza d'onda di 1060 nm, in quanto penetrando e
oltrepassando il dispositivo, non risulta influenzata dalla variazione di un parametro
essenzialmente superficiale che interessa solo i primi 3 µm della struttura. La lunghezza
d'onda di 407 nm, non risulta molto interessata da questo cambiamento, evidentemente
perchè la sua generazione ottica rimane tutta superficiale e non riesce a raggiungere la
profondità di giunzione. Ovviamente la radiazione che risulta più influenzata è quella
relativa a 783 nm, poichè la sua generazione ottica raggiunge le profondità interessate.
Anche i grafici della corrente in funzione del tempo ci riportano dei risultati congruenti
con quelli appena visti:
76
Simulazioni
Figura 67: 1060nm
Figura 68: 783nm
77
Simulazioni
Figura 69: 407nm
Influenza del contatto metallico
Per capire se l’incidenza del fascio ottico sul fotodiodo sia o meno influenzata dalla
presenza del contatto metallico, utilizziamo lo strumento Tecplot, tramite il quale
visualizzando la generazione ottica in presenza di contatti metallici di dimensioni diverse,
lasciando inalterati gli altri parametri del fotodiodo, riusciamo a vedere chiaramente le
differenze, qualora cene fossero) nella generazione ottica delle 4 strutture ,con un contatto
metallico di 0.2x0.2um, 0.4x0.4um, 0.6x0.6um, 1x1um e 2x2um rispettivamente. Il caso
considerato di seguito si riferisce al visibile(783nm).
Analisi con Tecplot
Tramite il software Tecplot si apprezzano evidenti differenze nella generazione ottica
delle tre strutture e ciò porta a supporre che il metodo considerato non trascuri l'esistenza
del contatto metallico e quindi la presenza del contatto metallico influenza la generazione
ottica.
78
Simulazioni
Figura 70: Generazione Ottica a) 0.2um b) 0.4um c) 0.6um d) 1um e) 2um
Analisi con inspect
Figura 71: Caduta di potenziale
Come si può notare c’è una evidente differenza anche nelle cadute di potenziale
visualizzate tramite inspect. Per cercare di spiegare questo fenomeno bisogna partire dalla
creazione del fotodiodo tramite il Sentaurus Device. Nel momento della scelta dei
materiali utilizzati( nel caso in esame metallo per la creazione del contatto di top), nel file
.grid creato da SDevice, vengono salvate le proprietà del materiale scelto, come la
79
Simulazioni
permittività, permeabilità, conducibilità, rifrattività ecc che poi vengono utilizzate per
creare un profilo più possibile realistico della struttura simulata e per poter cosi
visualizzare la corretta generazione ottica in corrispondenza di un fascio ottico che incide
il fotodiodo[7]. Quindi una volta utilizzato un materiale selezionato dalla lista Material
List, la sua traccia rimane nel file .grid e quindi il suo effetto non può essere trascurabile.
Per il metallo si considera la permittività e la permeabilità uguale a 1 e la conducibilità
uguale a 1x1030.
Variazione della potenza del fascio
Sono state eseguite prove con potenze del fascio laser pari a : 2x102 W/cm2, 2x103 W/cm2,
4x103 W/cm2, 5x 103 W/cm2, 2x 104 W/cm2, 5x104 W/cm2
Analisi con Inspect
Vediamo le cadute di potenziale per le tre lunghezze d’onda al variare della potenza:
Figura 72: 1060nm
80
Simulazioni
Figura 73: 783nm
Figura 74: 407nm
Da i grafici si vede che la caduta di potenziale per le tre lunghezze d’onda cresce al
crescere della potenza del fascio laser che incide il fotodiodo. Le cadute di potenziale più
rilevanti si incontrano nella lunghezza di 783nm e le cadute più piccole per la lunghezza
di 1060nm, esattamente come ci aspettavamo.
81
Simulazioni
Variazione del punto di incidenza
Lasciando inalterata la geometria del dispositivo, spostiamo di simulazione in
simulazione la posizione di incidenza del fasci laser sul fotodiodo e vediamo come questo
influenza i risultati delle simulazioni. Facciamo variare la finestra solo secondo la
direzione x.
In questo caso è interessante andare a vedere tramite Tecplot la generazione ottica. Si
prende come esempio di illustrazione il visibile (783nm).
Figura 75: Finestre di incidenza del fascio laser
Analisi con Tecplot
Figura 76: Generazione ottica ,finestra centrata in 0
82
Simulazioni
Figura 77: Generazione ottica, finestra di incidenza centrata in -1 e 1
83
Simulazioni
Figura 78: Generazione ottica, finestra di incidenza centrata in -2 e 2
84
Simulazioni
Figura 79: Generazione ottica, finestra di incidenza centrata in -4 e 4
Il comportamento visto a primo impatto non è quello che ci aspettavamo. Infatti le
finestre più centrali dovrebbero presentare una maggiore caduta di tensione rispetto alle
finestre più laterali, in quanto sono più vicine alla giunzione del dispositivo. E in base a
questo noi ci aspettavamo la maggiore generazione ottica quando la finestra è centrata in
0. La piccola generazione ottica che vediamo però potrebbe essere attribuito a quanto
detto prima sulla presenza del contatto metallico. Incidendo il fascio laser proprio sopra
al contato metallico, questo fa si che la generazione ottica sia inferiore(è come se il
metallo riflettesse l’illuminazione) . Per la finestra di incidenza centrata in -2 e 2, e in -1 e
85
Simulazioni
1, i risulatati sono più ragionevoli, quasi identici, essendo la struttura e la mesh utilizzata
perfettamente simmetrica. Infatti in quelle zone la carica risulta libera di muoversi.
Quello che si vede per le posizioni -4 e 4, non siamo in grado di spiegarlo con i strumenti
a nostra disposizione. Il motivo di questo andamento anomalo, può essere la presenza
degli effetti di bordo. Quando lo stimolo ottico incide un punto abbastanza laterale della
struttura, la carica non è libera di muoversi date le restrizioni fisiche del dispositivo e ciò
causa inevitabilmente un errore nella misura della generazione ottica e anche del
potenziale ai capi del fotodiodo.
Effetti di griglia
Un passo importante nella costruzione del dispositivo è la costruzione e la scelta della
mesh più adatta al nostro caso. Esso riveste un ruolo estremamente importante durante lo
svolgimento delle simulazioni[9]. Scegliere un numero di punti opportuno è spesso il
compito più arduo da svolgere, in quanto influenza la qualità dei risultati. Il numero di
punti va scelto in modo ragionato simulazione per simulazione: non deve essere troppo
elevato, ma neanche troppo ridotto altrimenti dall'eccessiva accuratezza si sfocia verso un
eccessiva grossolanità di calcolo. Quindi di norma vengono svolte delle prove con griglie
più o meno raffinate e confrontando i risultati, si riesce a scegliere la griglia migliore dal
punto di vista dell'accuratezza del risultato e della velocità di simulazione.
Le mesh utilizzate sono le seguenti:
86
Simulazioni
Analisi con Inspect
Figura 80: 1060nm
Figura 81: 783nm
87
Simulazioni
Figura 82: 407nm
Come era logico attendersi, la mesh da 735 punti non riesce a descrivere correttamente le
grandezze elettriche del dispositivo, siccome non applica nessuna differenza tra le zone
critiche dove varia il drogaggio. Le griglie che risultano migliori sono quella costituita da
5600 punti e 10310 punti. Dal momento che danno luogo a risultati molto prossimi tra
loro, infatti differiscono per qualche mV, si è deciso di utilizzare quella con 5600 nodi, in
quanto soddisfa sia la scelta di una mesh che caratterizzi più realisticamente possibile il
comportamento del dispositivo, sia i tempi di simulazione che non sono eccessivamente
lunghi.
88
CONCLUSIONI E SVILUPPI FUTURI
Questa tesi ha avuto come oggetto lo studio attraverso simulazioni tridimensionali, di
una particolare categoria di rivelatori di particelle a semiconduttore: i rivelatori APS. Si è
mostrato come software di simulazione possano essere utilizzati per caratterizzare
completamente dei sensori di radiazione e come le informazioni ottenute possano essere
interpretate per migliorarne lo sviluppo. Ogni minimo parametro tecnologico e
geometrico è stato analizzato, mostrando come sue eventuali variazioni possano
influenzare la risposta del sensore. I risultati hanno mostrato così la reazione del
dispositivo a diverse condizioni di utilizzo e hanno fornito dati interessati da sfruttare per
la progettazione del sensore, a seconda della lunghezza d'onda della radiazione da
rilevare.
Si è visto come il forte drogaggio del substrato limiti le prestazioni di questi sensori. La
carica raccolta, non dipende linearmente dallo spessore del substrato, dato che la regione
svuotata si estende solo per pochi micron al di sotto dell’impianto.
La struttura progettata e simulata in questo lavoro, consente di ottenere le migliori
prestazioni per la rilevazione di radiazioni aventi lunghezza d'onda dell'ordine dei 700
nm, in quanto la relativa generazione ottica avviene all'altezza della profondità di
giunzione e si ha una maggiore efficienza di raccolta di carica. Infatti non si sono ottenuti
risultati sufficientemente accurati per lunghezze d'onda troppo superiori (1060 nm) o
troppo inferiori (407 nm) a questa, in quanto la generazione ottica avviene troppo in
profondità o troppo in superficie nella struttura rispetto al livello raggiunto dalla
giunzione. Bisogna progettare opportunamente la profondità di giunzione a seconda della
lunghezza d'onda a cui deve risultare sensibile il fotodiodo. Un altro aspetto di particolare
interesse è stata la scelta di una mesh appropriata, dovendo fare un compromesso tra la
complessità di calcolo, tempi di calcolo e qualità dei risultati delle simulazioni. Per
riprodurne correttamente il funzionamento al simulatore `e necessario predisporre griglie
con un grande numero di nodi. All’interno di questi dispositivi poi, i fenomeni di
interesse sono circoscritti in regioni di dimensioni molto contenute: questo porta a dover
infittire la discretizzazione del dominio in queste zone, con conseguente ulteriore
aumento del numero di nodi da considerare. Griglie sufficientemente dettagliate tali da
permettere una descrizione affidabile del dispositivo richiedono tempi di calcolo
proibitivi, persino per delle macchine all’avanguardia come i calcolatori dell’ultima
Conclusioni e sviluppi futuri
generazione. Senza l’utilizzo del cluster di calcolo dell’INFN di Perugia, non sarebbe
stato possibile eseguire tutte queste analisi. L’accesso a questa potente rete di calcolo ha
cambiato totalmente l’approccio al lavoro di simulazione. Se prima, date le scarse risorse
computazionali a disposizione, il numero di simulazioni eseguibili per caratterizzare il
sensore era limitato, ora ogni minimo parametro può
essere analizzato a fondo. Alla luce dei risultati ottenuti si può osservare che per
incidenze simmetriche del fascio laser nelle zone più esterne del fotodiodo, non si
ottengono le medesime risposte in tensione. Questo problema non può che essere
attribuito agli effetti di bordo o a qualche caratteristica che non è legata alla struttura del
fotodiodo ma alla fonte del fascio, essendo la struttura del fotodiodo perfettamente
simmetrica e allo stesso modo anche la mesh applicata.
Risulta invece più chiaro l’influenza del contatto metallico nella risposta del dispositivo,
quando inciso dal fascio ottico. Lo Strumento Sentaurus Device memorizza l’impronta
del contatto nel file .grid, e ne tiene conto della sua presenza nel calcolo della generazione
ottica e di conseguenza anche nella risposta del dispositivo. Di sicuro si potrebbe provare
a sperimentare
nuovi modelli per la caratterizzazione ottica contenuti nella libreria di Sentaurus Device
in modo da capire più approfonditamente questo aspetto.
SVILUPPI FUTURI
Al fine di migliorare i risultati delle simulazioni si può lavorare sulle caratteristiche del
fascio ottico,cercare di capire come possono essere variate le sue proprietà, come la
potenza, l’angolo di incidenza, finestra di incidenza , essendo la struttura del fotodiodo e
la mesh applicata perfettamente simmetriche e con delle caratteristiche soddisfacenti.
90
BIBLIOGRAFIA
BIBLIOGRAFIA
[1] R.C.Jaeger Microelectronic Circuit Design, McGraw-Hill,1997.
[2] S. M. Sze Dispositivi a Semiconduttore
[3] C. Kitterl Introduction to Solid State Physics, J. Wiley
[4] D. Passeri, A. Marras, D. Biagetti, P. Placidi, P. Delfanti, L. Servoli, G.M. Bilei,
Characterization of Active Pixel Sensors fabricated in CMOS 0.18 µm
technology, Nucl. Instru. Meth A 582 (2007) 871–875.
[5] Daniele Biagetti, “Caratterizzazione elettrica e funzionale di sensori di
radiazione a pixel attivi integrati in tecnologia CMOS da 0.18µm” A.A.
2005/2006.
[6] Synopsys Advanced TCAD Tools User Manuals, www.synopsys.com
[7] Synopsys Sentaurus Device User Guide, September 2008.
[8] Synopsys TCAD Sentaurus Training.
[9] Synopsys Mesh Generation Tools User Guide,September 2008.
[10] INFN GRID Project https://grid.infn.it/
91