fenomeni magnetici fondamentali
25
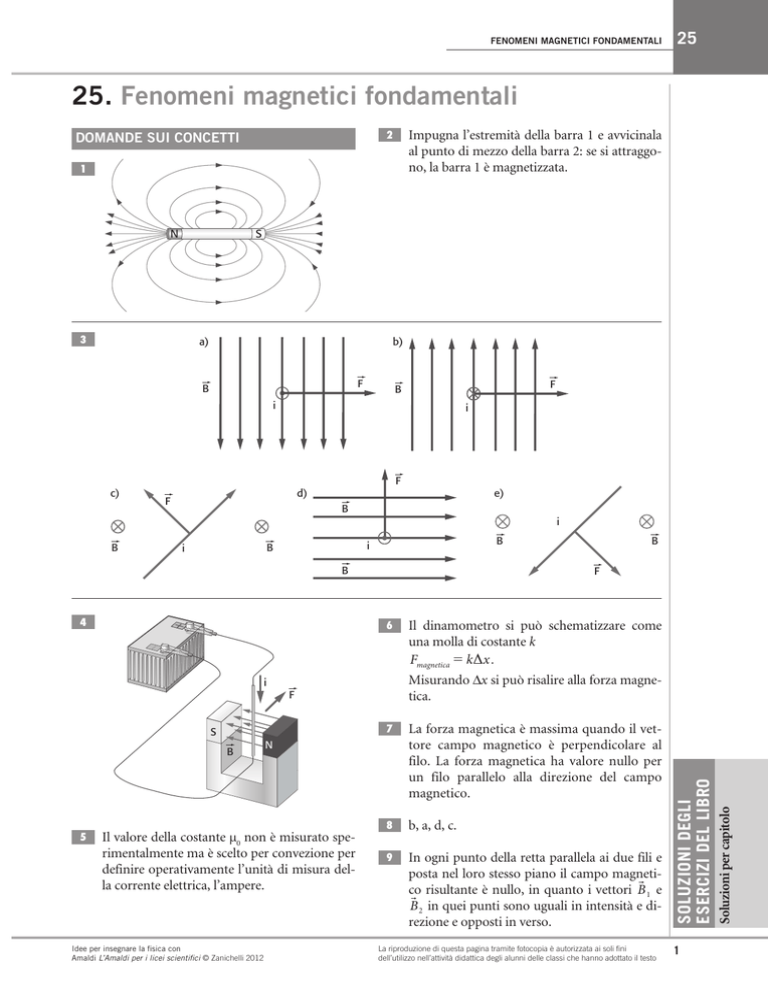
25. Fenomeni magnetici fondamentali
1
N
3
Impugna l’estremità della barra 1 e avvicinala
al punto di mezzo della barra 2: se si attraggono, la barra 1 è magnetizzata.
2
Domande sui concetti
S
a)
b)
F
B
F
B
i
i
c)
F
d)
F
e)
B
i
B
i
B
4
F
6
i
B
7
La forza magnetica è massima quando il vettore campo magnetico è perpendicolare al
filo. La forza magnetica ha valore nullo per
un filo parallelo alla direzione del campo
magnetico.
8
b, a, d, c.
9
In ogni punto della retta parallela ai due fili e
posta nel loro stesso piano il campo magnetiv e
co risultante è nullo, in quanto i vettori B
1
vB in quei punti sono uguali in intensità e di2
rezione e opposti in verso.
N
5
Il valore della costante μ0 non è misurato sperimentalmente ma è scelto per convezione per
definire operativamente l’unità di misura della corrente elettrica, l’ampere.
Idee per insegnare la fisica con
Amaldi L’Amaldi per i licei scientifici © Zanichelli 2012
Il dinamometro si può schematizzare come
una molla di costante k
Fmagnetica = kDx .
Misurando Dx si può risalire alla forza magnetica.
F
S
B
La riproduzione di questa pagina tramite fotocopia è autorizzata ai soli fini
dell’utilizzo nell’attività didattica degli alunni delle classi che hanno adottato il testo
1
Soluzioni per capitolo
B
i
soluzioni degli
esercizi del libro
B
fenomeni magnetici fondamentali
10 a) Asse x: d. Asse y: B.
b) Asse x: i. Asse y: B.
c) i costante.
11
Sì, se le correnti hanno verso opposto nel
punto d/2 i due campi magnetici sono uguali
in intensità e opposti in verso.
12
i
i
B
B
a) Non equilibrio
b) Equilibrio stabile
13
La condizione è di equilibrio instabile. L’angolo α fra i due vettori vale 180° e il suo seno
si annulla, ma ogni piccola rotazione della
spira attorno al suo asse la porta a ruotare ulteriormente fino alla condizione di equilibrio
stabile.
14
L’amperometro ha sempre una resistenza interna, poiché contiene una bobina di filo metallico in cui deve fluire la corrente da misurare. Un buon amperometro ha una piccola
resistenza interna.
15
Il voltmetro si usa per misurare la differenza
di potenziale a circuito chiuso, l’elettrometro
la misura a circuito aperto.
25
i
i
B
B
c) Non equilibrio
d) Equilibrio instabile
problemi
n0 i1 i2
l =c
n0 i1 i2
l =c
^ 2, 7 A h # ^ 6, 8 A h
4r # 10-7 N
# ^ 2, 00 m h = 4, 9 # 10-4 N
2 m#
2r
A
15 # 10-3 m
F=
F=
La forza è attrattiva.
l=
F fin = 2Fin = 2 # ^ 9, 5 # 10-6 N h = 1, 9 # 10-5 N
2r d
2r d
^ 2, 7 A h # ^ 6, 8 A h
4r # 10-7 N
# ^ 1, 00 m h = 2, 4 # 10-4 N
2 m#
2r
A
15 # 10-3 m
Fm d
^ 9, 5 # 10-6 N h # ^ 3, 2 # 10-1 m h
=
= 5, 3 m
k m i 1 i 2 ^ 2 # 10-7 N/A2 h # ^ 1, 7 A h # ^ 1, 7 A h
i1 i2
i i
^ 3, 21 A h # ^ 3, 21 A h
l segue che d = k m 1 2 l = ^ 2 # 10-7 N/A2 h #
# ^0, 68 m h =
d
F
2, 1 # 10-5 N
= 6, 7 # 10-2 m .
4
Da F = k m
5
La forza è nulla perché una delle correnti vale zero.
DV
l
; per la seconda legge di Ohm: R = t ; quindi:
Per la prima legge di Ohm è: i =
R
S
Idee per insegnare la fisica con
Amaldi L’Amaldi per i licei scientifici © Zanichelli 2012
La riproduzione di questa pagina tramite fotocopia è autorizzata ai soli fini
dell’utilizzo nell’attività didattica degli alunni delle classi che hanno adottato il testo
2
Soluzioni per capitolo
3
soluzioni degli
esercizi del libro
2
fenomeni magnetici fondamentali
DV
i=
F = km
t l/ S
=
25
SDV
. Risulta pertanto:
tl
i1 i2
6SDV/ ^ tl h@2
S2 DV2
=
l = km
l = km 2
d
d
t ld
-6
2 2
^ 3 # 10 m h # ^ 20 V h2
= ^ 2 # 10-7 N/A2 h #
=
^ 1, 7 # 10-8 X $ m h2 # ^ 1, 20 m h # ^ 43 # 10-2 m h
= ^ 2 # 10-7 N/A2 h #
^ 9 # 10-12 m 4 h # ^ 40 # 10 V 2 h
= 4, 8 N .
^ 2, 89 # 10-16 X2 $ m 2 h # ^ 1, 20 m h # ^ 43 # 10-2 m h
La forza che agisce sul filo 1 è Fv1 = Fv ^ 2 h + Fv ^ 3 h , dove:
i i
i i
F ^ 2 h = k m 1 2 l, forza generata da i2 su i1; F ^ 3 h = k m 1 3 l , forza generata da i3 su i1.
d
d
Ne consegue che F ^ 2 h = F ^ 3 h . L’angolo compreso tra i due vettori Fv ^ 2 h e Fv ^ 3 h è di 60°. Da considerazioni geometriche sui triangoli rettangoli con angoli di 30° e 60°, possiamo dire che F1 = F ^ 2 h 3 .
Essendo
6
F^2 h = k m
i1 i2
^2 A h # ^2 A h
l = ^ 2 # 10-7 N/A2 h #
# ^ 1 m h = 2, 29 # 10-6 N ,
d
0, 35 m
risulta: F1 = F ^ 2 h 3 = 4 # 10-6 N .
8
9
Sulla barra agiscono due forze:
– la forza-peso, diretta verticalmente verso il basso: Fvp = mgv ;
– la forza magnetica, che per essere diretta verso l’alto deve essere prodotta da una corrente i con verso
da destra a sinistra: Fm = Bil.
Perché la barra si sollevi, occorre che sia Fm 2 Fp, ossia Bil 2 mg, da cui segue:
i2
10
F = Bil = ^ 0, 10 T h # ^ 0, 70 m h # ^ 0, 070 A h = 4, 9 # 10-3 N
^ 1, 2 # 10-1 kg h # ^ 9, 8 m/s2 h
mg
=
= 6 # 10 A.
Bl
^ 8 # 10-2 T h # ^ 2, 3 # 10-1 m h
F1
F
F
F
, mentre da F2 = Bi 2 l segue lB = 2 , quindi risulta 1 = 2 , da cui segue:
i1
i2
i1
i2
i
8, 7 A
i 1 = F1 2 = ^ 7 # 10-3 N h #
= 1 A.
F2
4, 9 # 10-2 N
Da F1 = Bi 1 l segue lB =
Idee per insegnare la fisica con
Amaldi L’Amaldi per i licei scientifici © Zanichelli 2012
La riproduzione di questa pagina tramite fotocopia è autorizzata ai soli fini
dell’utilizzo nell’attività didattica degli alunni delle classi che hanno adottato il testo
3
Soluzioni per capitolo
Sui lati AB e CD agiscono forze uguali e opposte, mentre
n 0 ii q a
n 0 ii q a
1h
2h
F^AC
=
F^AC
=
2rl
2r ^ d - l h
n 0 ii q a
n 0 ii q a
1h
2h
.
F^BD
=F^BD
=2r ^ l + a h
2r ^ d - l - a h
All’equilibrio la risultante delle forze deve essere nulla
1
1
1
1
+
=0
l l+a d-l d-l-a
l ^ - 2d h + d ^ d - a h = 0
a = d - 2l = 1, 0 m - 2 # 2, 5 # 10-1 m = 50 cm .
soluzioni degli
esercizi del libro
7
fenomeni magnetici fondamentali
11
Prima del passaggio della corrente, l’asta lunga l con sezione S è soggetta a una forza-peso di modulo
Fpi = mg = ^ dlS h g. Nel momento in cui circola una corrente i, il peso dell’asta diminuisce per la presenza del campo magnetico terrestre. Allora la forza-peso dell’asta in presenza della corrente sarà:
Fpf = m ^ g - a m h, dove am rappresenta un’accelerazione verso l’alto dovuta alla forza magnetica:
Fm
F
" Fpf = m c g - m m " Fm = Fpi - Fpf .
m
m
am =
Se il peso è diminuito dello 0,128% allora significa che la forza magnetica ha un’intensità pari al valore
0, 128
di questa diminuzione: Fm =
F . Essendo Fm = Bil , risulta:
100 pi
dSg
0, 128
0, 128
^ dlS h g = Bil, da cui segue: B = ^ 1, 28 # 10-3 h
Fpi = Bil, ossia
=
100
100
i
^ 2, 6 # 103 kg/m 3 h # ^ 1, 0 # 10-6 m 2 h # ^ 9, 8 m/s2 h
= ^ 1, 28 # 10-3 h #
= 2, 0 # 10-5 T.
1, 6 A
12
25
Sul filo agisce una forza magnetica diretta lungo il piano orizzontale a cui si oppone la forza d’attrito
ilB - n D mg = ma
ilB - n D mg
a=
m
v = v 0 + at = at
ilB - n D mg
mt
v =c
m
v
m a k + n D mg
t
B=
il
0, 5 m/s
m + 0, 102 # 0, 100 kg # 9, 8 m/s2
0, 100 kg # c
10 s
B=
= 0, 5 T.
2 A # 0, 1 m
13
Da F = Bil sen a, segue sen a =
F
, ossia
Bil
1, 28 # 10-2 N
F
= arcsen
=
Bil
^ 4, 00 # 10-1 T h # ^ 3, 20 # 10-1 A h # ^ 2, 00 # 10-1 m h
= arcsen ^ 5 # 10-1 h = 30c .
Anche un valore dell’angolo di 150° è accettabile.
a = arcsen
15
v , risulta F = Bil sen a.
Essendo Fv = i vl # B
-1
-1
Se a = 90 c , allora F = Bil sen 90 c = Bil = ^ 5 , 0 # 10 T h # ^ 5 , 0 A h # ^ 1 , 0 # 10 m h = = 25 # 10-2 N .
16
Se a = 90c - 30c = 60c , allora
3
3
=
# ^ 5, 0 # 10-1 T h # ^ 5, 0 A h # ^ 1, 0 # 10-1 m h = 22 # 10-2 N.
2
2
Se a = 90 c - 30 c = 60 c , allora
3
3
F = Bil sen 60c = Bil
=
# ^ 5, 0 # 10-1 T h # ^ 5, 0 A h # ^ 1, 0 # 10-1 m h = 22 # 10-2 N.
2
2
Se a = 0 c , allora F = Bil sen 0 c = 0 N .
F = Bil sen 60c = Bil
La forza-peso della barra è espressa da: Fp = Vd Al g = Sld Al g, mentre la corrente che circola nella barra
l
SDV
.
è tale che DV = t Al i, ossia vale: i =
S
t Al l
Idee per insegnare la fisica con
Amaldi L’Amaldi per i licei scientifici © Zanichelli 2012
La riproduzione di questa pagina tramite fotocopia è autorizzata ai soli fini
dell’utilizzo nell’attività didattica degli alunni delle classi che hanno adottato il testo
4
Soluzioni per capitolo
soluzioni degli
esercizi del libro
fenomeni magnetici fondamentali
Quindi la forza magnetica che agisce sulla barra è:
SDV
BSDV sen a
Fm = Bil sen a = B
l sen a =
.
t Al l
t Al
Perché la barra si sollevi deve essere Fm 2 Fp, ossia
DV 2
BSDV sen a
t Al
25
2 Sld Al g, da cui segue:
Sld Al t A1 g
ld t g
= Al Al =
BS sen a
B sen a
^ 7, 50 # 10-1 m h # ^ 2, 960 # 103 kg/m 3 h # ^ 2, 8 # 10-8 X $ m h # ^ 9, 8 m/s2 h
=
= 25 V .
^ 4, 80 # 10-5 T h # ^ 1/2 h
v . La forza Fv giace nel piano individuato dai vettori B
v e B
v . Chiamiamo
Ricordiamo che Fv = i vl # B
O
V
v e Fv la componente della forza dovuta a B
v .
FvO la componente della forza dovuta a B
O
V
V
v . Risulta: F = B il = ^ 2 # 10-5 T h # ^ 2, 0 m h # ^ 20 A h = 8 # 10-4 N , con Fv
Calcoliamo FvO = i vl # B
O
O
0
diretta verticalmente verso il basso.
v . Risulta:
Calcoliamo ora FvV = i vl # B
V
-5
v e
FV = B V il = ^ 6 # 10 T h # ^ 2, 0 m h # ^ 20 A h = 2, 4 # 10-3 N , con FvV diretta parallelamente a B
O
con lo stesso verso.
Consideriamo Fv = FvO + FvV . Siccome FvO e FvV sono perpendicolari, il modulo di Fv vale:
F = F O2 + F V2 = ^ 8 # 10-4 N h2 + ^ 2, 4 # 10-3 N h2 = 3 # 10-3 N .
Il vettore Fv si trova su un piano verticale e, rispetto alla verticale orientata verso il basso, è deviato verso Nord e forma con FvO un angolo
17
a = arctg
18
FV
2, 4 # 10-3 N
= arctg
= arctg 3 , 72c .
FO
8 # 10-4 N
kDy - mg = 0
mg
k=
Dy
Con il campo magnetico:
iBl - kDyl - mg = 0
iBl -
^ 2 # 10-7 N/A2 h # ^ 2, 0 A h
n0 i
=
= 8, 0 # 10-7 T
2r d
5, 0 # 10-1 m
19
B=
20
Da B = k m
21
Da
-4
Bd ^ 2, 5 # 10 T h # ^ 150 m h
i
segue che i =
=
= 1, 9 # 105 A.
d
km
2 # 10-7 N/A2
B = km
d = km
^ 2 # 10-7 N/A2 h # ^ 1, 2 # 103 A h
i
i
= 0, 5 m .
segue che d = k m =
d
B
5 # 10-4 T
^ 2 # 10-7 N/A2 h # ^ 1, 9 # 105 A h
i
=
= 8 # 10 m
B
5 # 10-4 T
Idee per insegnare la fisica con
Amaldi L’Amaldi per i licei scientifici © Zanichelli 2012
La riproduzione di questa pagina tramite fotocopia è autorizzata ai soli fini
dell’utilizzo nell’attività didattica degli alunni delle classi che hanno adottato il testo
5
Soluzioni per capitolo
soluzioni degli
esercizi del libro
mg
Dyl - mg = 0
Dy
mg Dyl
d
B=
+ 1n
il Dy
^ 0, 102 kg h # ^ 9, 8 m/s2 h
B=
# ^ 2 + 1 h = 1, 0 T.
^ 30 A h # ^ 0, 10 m h
fenomeni magnetici fondamentali
25
v =B
v +B
v . B
v e B
v sono vettori perpendicolari (in ogni pun Il campo magnetico complessivo è: B
A
B
A
B
v ha direzione perpendicolare al piano.
to) al piano che contiene i due fili conduttori, quindi anche B
Assumiamo che i tre vettori abbiano verso positivo quando sono orientati verso l’alto.
v in P .
Valore di B
1
v
B A è diretto verso il basso e il suo modulo vale:
n
i
2, 0 A
B A = 0 A = ^ 2 # 10-7 N/A2 h #
= 2, 0 # 10-5 T.
2r P1 A
2, 0 # 10-2 m
v è diretto verso l’alto e il suo modulo vale:
B
B
23
iB
3, 0 A
= ^ 2 # 10-7 N/A2 h #
= 5, 0 # 10-6 T.
2r P1 B
12 # 10-2 m
n0
BB =
Quindi risulta:
B =- B A + B B = ^ - 2, 0 # 10-5 T h + ^ 5, 0 # 10-6 T h =- 1, 5 # 10-5 T.
v in P .
Valore di B
2
v è diretto verso l’alto e il suo modulo vale:
B
A
n
i
2, 0 A
B A = 0 A = ^ 2 # 10-7 N/A2 h #
= 1, 0 # 10-5 T. 2r P2 A
4, 0 # 10-2 m
v è diretto verso l’alto e il suo modulo vale:
B
B
n
i
3, 0 A
B B = 0 B = ^ 2 # 10-7 N/A2 h #
= 1, 0 # 10-5 T.
2r P2 B
6, 0 # 10-2 m
v è diretto verso l’alto e il suo modulo vale:
Allora B
B = B A + B B = ^ 1, 0 # 10-5 T h + ^ 1, 0 # 10-5 T h = 2, 0 # 10-5 T
v in P .
di B
3
vB è diretto verso l’alto e il suo modulo vale:
A
BA =
v è diretto verso il basso e il suo modulo vale:
B
B
Valore
iA
2, 0 A
= ^ 2 # 10-7 N/A2 h #
= 3, 1 # 10-6 T.
2r P3 A
13 # 10-2 m
n0
n
i
3, 0 A
B B = 0 B = ^ 2 # 10-7 N/A2 h #
= 2, 0 # 10-5 T.
2r P3 B
3, 0 # 10-2 m
Quindi:
B = B A - B B = ^ 3, 1 # 10-6 T h - ^ 2, 0 # 10-5 T h =- 1, 7 # 10-5 T.
v . Abbiamo quindi la seguente ca Rispetto al caso precedente, cambia solamente il verso del vettore B
B
sistica.
v in P .
Valore di B
1
v
B B è diretto verso il basso e
n
i
3, 0 A
B B = 0 B = ^ 2 # 10-7 N/A2 h #
= 5, 0 # 10-6 T,
2r P1 B
12 # 10-2 m
B =- B A - B B = ^ - 2, 0 # 10-5 T h - ^ 5, 0 # 10-6 T h =- 2, 5 # 10-5 T.
v in P .
Valore di B
2
vB è diretto verso il basso e
B
BB =
iB
3, 0 A
= ^ 2 # 10-7 N/A2 h #
= 1, 0 # 10-5 T,
2r P2 B
6, 0 # 10-2 m
n0
B = B A - B B = ^ 1, 0 # 10-5 T h - ^ 1, 0 # 10-5 T h = 0 T.
Idee per insegnare la fisica con
Amaldi L’Amaldi per i licei scientifici © Zanichelli 2012
La riproduzione di questa pagina tramite fotocopia è autorizzata ai soli fini
dell’utilizzo nell’attività didattica degli alunni delle classi che hanno adottato il testo
6
Soluzioni per capitolo
soluzioni degli
esercizi del libro
24
fenomeni magnetici fondamentali
25
27
200 # ^ 4, 89 A h
Ni ^
= 4r # 10-7 N/A2 h #
= 2, 1 # 10-3 T
l
5, 8 # 10-1 m
^ 2, 1 # 10-3 T h # ^ 7, 2 # 10-1 m h
Bl
i =
=
= 6, 1 A
n0 N
^ 4r # 10-7 N/A2 h # 200
Il campo magnetico è determinato dalla relazione: B =
29
30
2R
=
2
2 ^ R2 + y2 h3
.
^ 4r # 10-7 N/A2 h # ^ 4, 89 A h
= 9, 6 # 10-5 T.
2 # ^ 3, 2 # 10-2 m h
n 0 iR
2
2 ^ R2 + y h
2 3
=
^ 4r # 10-7 N/A2 h # ^ 4, 89 A h # ^ 3, 2 # 10-2 m h2
3
2 # 6^ 3, 21 # 10-2 m h2 + ^ 2, 00 # 10-2 m h2@
= 5, 9 # 10-5 T.
Sull’asse della spira, a 6,00 cm dal centro, è y = 6, 00 cm e
B=
n 0 iR
2
2 ^ R2 + y2 h3
=
^ 4r # 10-7 N/A2 h # ^ 4, 89 A h # ^ 3, 2 # 10-2 m h2
3
2 # 6^ 3, 2 # 10-2 m h2 + ^ 6, 00 # 10-2 m h2@
= 1, 0 # 10-5 T.
v =B
v +B
v . Siccome le due correnti hanno verso
Il campo magnetico totale dovuto alle due spire è B
1
2
opposto risulta B = B 1 - B 2 .
n0 i
n0 i
n0 i
1
1
c
m=
2 R2
2 R1 R2
^ 4r # 10-7 N/A2 h # ^ 8, 5 A h
1
1
-5
=
#c
m = 4, 4 # 10 T
2
4, 5 # 10-2 m 7, 2 # 10-2 m
n0 i1
n i
i
i
Dalla condizione B = B 1 - B 2 =
- 0 2 = 0 segue 1 = 2 , quindi deve essere:
R1 R2
2 R1
2 R2
R
4, 5 # 10-2 m
i 1 = i 2 1 = ^ 8, 5 A h #
= 5, 3 A.
R2
7, 2 # 10-2 m
n0 i
n 0 iR
Sull’asse della spira, a 2,00 cm dal centro, è y = 2, 00 cm e
B=
Nel centro della spira è y = 0 cm e
B=
B = n0
B=
2 R1
-
=
Numero delle spire nel solenoide: N =
Idee per insegnare la fisica con
Amaldi L’Amaldi per i licei scientifici © Zanichelli 2012
ls
20, 0 cm
=
= 400.
df
0, 050 cm
La riproduzione di questa pagina tramite fotocopia è autorizzata ai soli fini
dell’utilizzo nell’attività didattica degli alunni delle classi che hanno adottato il testo
7
Soluzioni per capitolo
28
B - Bl
= 0, 01
Bl
B
Bl =
^ 1 + 0, 01 h
n0 i
B
=
2r8l ^ 1 + 0, 01 h
16r # 1, 0 # 10-5 T # 1, 01 m
16rBl
i=
=
= 4, 0 # 102 A
n 0 ^ 1 + 0, 01 h
4r # 10-7 N/A2 # 1, 01
soluzioni degli
esercizi del libro
v in P .
Valore di B
3
v è diretto verso l’alto e
B
B
n
i
3, 0 A
B B = 0 B = ^ 2 # 10-7 N/A2 h #
= 2, 0 # 10-5 T,
2r P3 B
3, 0 # 10-2 m
B = B A + B B = ^ 3, 1 # 10-6 T h + ^ 2, 0 # 10-5 T h = 2, 3 # 10-5 T.
25
fenomeni magnetici fondamentali
25
Lunghezza del filo conduttore: l f = rd s N = 3, 14 # ^ 5, 00 # 10-2 m h # 400 = 62, 83 m .
2
-4
df 2
n = 3, 14 # c 5, 0 # 10 m m = 1, 96 # 10-7 m 2 .
2
2
lf i
SDV
Ni
NSDV
, quindi la
Dalle leggi di Ohm risulta DV = t , da cui segue i =
e B = n0
= n0
ls
S
tl f
tl s l f
differenza di potenziale vale:
Sezione del filo conduttore: S = r d
DV =
31
tBl s l f
n 0 NS
^ 1, 7 # 10-8 X $ m h # ^ 1, 26 # 10-3 T h # ^ 2, 00 # 10-1 m h # ^ 62, 83 m h
= 2, 7 V .
^ 4r # 10-7 N/A2 h # 400 # ^ 1, 96 # 10-7 m 2 h
=
Fissiamo l’origine nel centro della prima spira e scegliamo come asse positivo quello che va dalla prima spira verso la seconda.
n0 i1 R
n0 i2 R
2
2
2 ^ R2 + d2 h2
3
-
2 6R2 + ^ h - d h2@ 2
3
=0
3
i1
2
R2 + d2
=< 2
F
i2
R + ^ h - d h2
2
R2 + d2
3
2 = a
2
R + ^h - d h
R =>
R =>
32
a 3 ^h - d h - d
2
2
2
2
1 - a3
H
1
2
^ 0, 1 h3 ^ 1, 1 m - 0, 10 m h2 - ^ 0, 10 h2
2
1 - ^ 0, 1 h3
2
1
2
H = 51 cm
v segue n = iA = ^ 4, 5 A h # ^ 1, 27 # 10-3 m 2 h = 5, 7 # 10-3 A $ m 2 .
Da nv m = iA
m
v
v
v
Da M = n m # B segue M = n m B sen a.
Il valore massimo corrisponde al caso in cui sen a = 1:
M max = n m B = ^ 5, 7 # 10-3 A $ m 2 h # ^ 3, 5 # 10-5 T h = 2, 0 # 10-7 N $ m .
Area della spira: A = l 1 l 2 = ^ 2, 5 # 10-2 m h # ^ 7, 8 # 10-2 m h = 1, 95 # 10-3 m 2 .
v segue n = iA = ^ 3, 5 A h # ^ 1, 95 # 10-3 m 2 h = 6, 825 # 103 A $ m 2 .
Da nv = iA
33
m
m
Essendo M = n m B sen a , ossia sen a =
a = arcsen c
M
nm B
, risulta:
Risulta pertanto:
Spira quadrata: 2p = 4l " l =
r
nq
nc
=
r
r
i ^ p2 /4 h r
= .
i ^ p2 /rh 4
Idee per insegnare la fisica con
Amaldi L’Amaldi per i licei scientifici © Zanichelli 2012
La riproduzione di questa pagina tramite fotocopia è autorizzata ai soli fini
dell’utilizzo nell’attività didattica degli alunni delle classi che hanno adottato il testo
8
Soluzioni per capitolo
2
p
p2
v " n = iA = i p .
" A q = l2 = ; nv q = iA
q
q
2
4
4
2
p
p
p2
2
v
Spira circolare: 2p = 2rR " R = " A c = rR = ; nv c = iA " n c = iA c = i .
34
soluzioni degli
esercizi del libro
5, 5 # 10-6 N $ m
M
F = arcsen ^0, 11 h = 6, 5c .
m = arcsen <
^ 6, 825 # 10-3 A $ m 2 h # ^ 7, 1 # 10-3 T h
nm B
fenomeni magnetici fondamentali
35
36
25
er ragioni di simmetria la forza magnetica che agisce su ognuno dei due lati verticali ha lo stesso
P
v , allora
modulo e la stessa direzione, ma verso opposto. Siccome i lati sono perpendicolari a B
Fl = Bil sen 90c = Bil = ^ 2, 1 # 10-2 T h # ^ 1, 3 A h # ^ 3, 00 # 10-2 m h = 8, 2 # 10-4 N.
Per ragioni di simmetria la forza magnetica che agisce sui due lati inclinati è la stessa in modulo e
v , quindi
direzione, ma opposta in verso. I lati formano un angolo di 45° con il campo B
8, 2 # 10-4 N
1
Fl = Bil sen 45c = Bil
=
= 5, 8 # 10-4 N .
2
2
1
2
-2
-3
= 1, 7 # 10-5 N $ m
M = AiB sen 45 c = ^ 3, 00 # 10 m h # ^ 1, 3 A h # ^ 21 # 10 T h #
2
q = 2rrm
q
2rrm
i= =
= ~rm
T
2r
~
2
n m = iS = ~rmrr
n m = rm~r
3
r =a
rm~
k3 = c
1
1
3
27 # 10-3 A $ m 2
m = 30 cm
-2
r # 3, 18 # 10 cm # 10, 0 rad/s
38
Determiniamo la resistenza equivalente delle tre resistenze (le due dello schema più il voltmetro) in
parallelo:
R1 R2 RV
=
R eq =
R1 R2 + R1 RV + R2 RV
^ 55 X h # ^ 35 X h # ^ 4, 00 # 103 X h
= 21, 3 X.
^ 55 X h # ^ 35 X h + ^ 35 X h # ^ 4, 00 # 103 X h + ^ 55 X h # ^ 4, 00 # 103 X h
39
40
In questo modo si misura l’intensità della corrente che attraversa la resistenza di 45 Ω.
La caduta di tensione ai capi delle due coppie di resistenze in parallelo è la stessa, quindi:
R eq = ^ 45 X h + ^ 2, 50 # 10-3 X h = 45, 0025 X,
DV
120 V
DV = R eq i " i =
=
= 2, 7 A.
R eq
45, 0025 X
i1 è la corrente che passa nel ramo BAC. i2 è la corrente che attraversa BDC.
i1 passa in Rx e R3 e i2 passa in R1 e R2, poiché l’amperometro non segna corrente. Quindi
Idee per insegnare la fisica con
Amaldi L’Amaldi per i licei scientifici © Zanichelli 2012
soluzioni degli
esercizi del libro
V A = VD
Quindi
i1 Rx = i2 R1
i1 R3 = i2 R2
i2 Rx R3
=
=
i1 R1 R2
R
30 X
= 20 X
R x = R 1 3 = 10 X #
R2
15 X
La riproduzione di questa pagina tramite fotocopia è autorizzata ai soli fini
dell’utilizzo nell’attività didattica degli alunni delle classi che hanno adottato il testo
9
Soluzioni per capitolo
nm
fenomeni magnetici fondamentali
25
problemi generali
v e B
v sono perpendicolari al piano individuato dai due fili. Stabiliamo
I vettori campo magnetico B
r
s
per convenzione che abbiano verso positivo quando sono uscenti dal foglio.
Punto A:
v =B
v +B
v " B = B - B = n0 ir - n0 is = n0 d ir - is n =
B
r
s
r
s
2r d r 2r d s 2r d r d s
-7
2
5, 0 A
3, 0 A
4r # 10 N/A
=
#c
m =- 5, 0 # 10-6 T.
-2
2r
4, 0 # 10 m 2, 0 # 10-2 m
1
Punto B:
v =B
v +B
v " B =- B - B =- n 0 i r - n 0 i s =- n 0 d i r + i s n =
B
r
s
r
s
2r d r 2r d s
2r d r d s
5, 0 A
3, 0 A
=- ^ 2 # 10-7 N/A2 h # c
+
m =- 5, 5 # 10-5 T.
4, 0 # 10-2 m 2, 0 # 10-2 m
Punto C:
v =B
v +B
v " B =- B + B =- n 0 i r + n 0 i s = n 0 d - i r + i s n =
B
r
s
r
s
2r d r 2r d s 2r
dr ds
= ^ 2 # 10-7 N/A2 h # c -
5, 0 A
3, 0 A
+
m = 5, 0 # 10-6 T.
-2
4, 0 # 10 m 2, 0 # 10-2 m
Punto D:
v =B
v +B
v " B = B + B = n0 ir + n0 is = n0 d ir + is n =
B
r
s
r
s
2r d r 2r d s 2r d r d s
5, 0 A
3, 0 A
= ^ 2 # 10-7 N/A2 h # c
+
m = 5, 5 # 10-5 T.
4, 0 # 10-2 m 2, 0 # 10-2 m
Affinché il campo magnetico totale si annulli nel centro della spira, occorre che sia B f = B s .
n if
n i
Essendo B f = 0
e B s = 0 s , deve risultare:
2 R
2r d
-2
Ri f
^ 3, 0 # 10 m h # ^ 3, 2 A h
=
= 0, 61 A.
is =
rd
3, 14 # ^ 5, 0 # 10-2 m h
2
1
4
2
→
B2
B
2
i2
→
B1
1
i1
A
1
2
n 0 iR
Il campo magnetico è espresso dalla relazione: B =
.
2 ^ R2 + y2 h3
d
R
1) Nel centro del sistema a y = = k:
2
2
Idee per insegnare la fisica con
Amaldi L’Amaldi per i licei scientifici © Zanichelli 2012
La riproduzione di questa pagina tramite fotocopia è autorizzata ai soli fini
dell’utilizzo nell’attività didattica degli alunni delle classi che hanno adottato il testo
10
Soluzioni per capitolo
Nei punti A e B il modulo dei campi magnetici generati dai due fili è lo
stesso:
n i
2, 0 A
B 1 = B 2 = 0 = ^ 2 # 10-7 N/A2 h #
= 8, 0 # 10-8 T.
2r d
5, 0 m
Per ragioni di simmetria il campo magnetico in B ha lo stesso modulo, la
stessa direzione (perpendicolare al piano individuato dai due fili) e lo stesso verso che possiede in A.
v è perpendicolare al segFacciamo riferimento allo schema di figura: B
1
v
mento che unisce 1 con B e B 2 è perpendicolare al segmento che unisce
v e B
v
2 con B. Quindi, poiché il triangolo 12B è equilatero, i vettori B
1
2
formano tra loro un angolo di 120°. Applicando la regola del parallelogramma otteniamo:
v =B
v +B
v " B = B = 8, 0 # 10-8 T.
B
soluzioni degli
esercizi del libro
3
fenomeni magnetici fondamentali
B1 =
B2 =
n 0 iR
2
+
Chiamiamo x la distanza fra i due fili. I fili sono soggetti a due forze:
– forza di Hooke (di richiamo elastica): FvH =- k H Dxv;
i i
– forza magnetica (repulsiva in questo caso): Fvm = k m 1 2 vl .
x
Su ciascun filo agisce una forza risultante Fv = FvH + Fvm . Se il sistema è in equilibrio è ovviamente
Fv = 0, ossia FvH + Fvm = 0, quindi FH = Fm:
k
i i
i i
k H Dx = k m 1 2 l " k H ^ x - x 0 h = k m 1 2 l " x 2 - x 0 x - m i 1 i 2 l = 0 ,
x
x
kH
k
x 0 ! x 20 + 4i 1 i 2 l m
kH
=
x 1, 2 =
2
4 # ^0, 25 A h # ^1, 1 A h # ^1, 0 m h # ^2 # 10-7 N/A2 h
^ 7, 2 # 10-1 m h ! ^ 7, 2 # 10-1 m h2 +
5, 6 # 10-6 N/m
=
=
2
=
^ 7, 2 # 10-1 m h ! ^ 7, 2 # 10-1 m h2 + ^ 3, 9 # 10-2 m 2 h
=
2
^ 7, 2 # 10-1 m h ! ^ 52 # 10-2 m 2 h + ^ 3, 9 # 10-2 m 2 h
=
=
2
7, 35 # 10-1 m
^ 7, 2 # 10-1 m h ! 56 # 10-2 m 2
^ 7, 2 # 10-1 m h ! ^ 7, 5 # 10-1 m h
=
=
=)
2
2
- 1, 5 # 10-1 m
Idee per insegnare la fisica con
Amaldi L’Amaldi per i licei scientifici © Zanichelli 2012
La riproduzione di questa pagina tramite fotocopia è autorizzata ai soli fini
dell’utilizzo nell’attività didattica degli alunni delle classi che hanno adottato il testo
11
Soluzioni per capitolo
n0 i
soluzioni degli
esercizi del libro
5
2
n i
n0 i
n i 2 2 +1
o.
= 0 +
= 0 e
2R 2 ^ R2 + R2 h3
2R 4 2R
2R
2 2
Il rapporto tra il campo magnetico nel centro del sistema e il campo magnetico nel centro della prima spira vale pertanto:
8n 0 i
5 5R
= 1, 1.
n0 i 2 2 + 1
e
o
2R
2 2
è il valore del campo magnetico generato dalla prima spira nel centro del sistema;
n 0 iR
B = B1 + B2 =
2 ^ R2 + d2 /4 h3
Nel centro del sistema i campi magnetici generati dalle spire hanno lo stesso verso e sono paralleli,
quindi per trovare il campo magnetico totale basta sommare i loro moduli:
2
è il valore del campo magnetico generato dalla seconda spira nel centro del sistema.
2 ^ R2 + d2 /4 h3
Nel centro del sistema i campi magnetici generati dalle spire, percorse da correnti di uguale intensità e verso, hanno lo stesso verso e sono paralleli, quindi per trovare il campo magnetico totale basta
sommare i loro moduli:
2
2
2
2
n 0 iR
n 0 iR
n 0 iR
n 0 iR
B = B1 + B2 =
+
=
+
=
2 ^ R2 + d2 /4 h3 2 ^ R2 + d2 /4 h3
2 ^ R2 + R2 /4 h3 2 ^ R2 + R2 /4 h3
2
2
8n 0 i
n 0 iR
n 0 iR
=
=
=
.
^ R2 + R2 /4 h3
R3 ^ 5 5 /8 h 5 5 R
2) Nel centro della prima spira:
n i
B 1 = 0 è il valore del campo magnetico generato dalla prima spira nel suo centro;
2R
2
n 0 iR
è il valore del campo magnetico generato dalla seconda spira nel centro della prima.
B2 =
2 ^ R2 + R2 h3
n 0 iR
25
fenomeni magnetici fondamentali
Non essendo accettabile la soluzione negativa, risulta:
Dx = x - x 0 = ^ 7, 35 # 10-1 m h - ^ 7, 2 # 10-1 m h = 0, 15 # 10-1 m = 1, 5 # 10-2 m .
DV
. Se la forza è complessivamente attrattiva, allora la forza
R
tra il filo e il lato della spira che gli è più vicino deve essere attrattiva.
Il valore della forza che il filo esercita sul lato della spira che gli è più vicino (attrattiva) è:
n is i f
F1 = 0
l, dove l è la lunghezza del lato della spira.
2r d
Il valore della forza che il filo esercita sul lato della spira che gli è più lontano (repulsiva) è:
n is i f
l.
F2 = 0
2r d + l
La forza totale è Fv = Fv1 + Fv2 e in modulo:
2
n0 is i f l 1
n0 is i f l
n0 is i f l
n0 is i f
n0 is i f
1
l
F = F1 - F2 =
ll=
=
.
a k=
2 r d ^ d + l h 2 rd ^ d + l h
2r d
2r d + l
2r
d d+l
Risulta quindi:
is =
La resistenza elettrica della spira vale:
R=
La corrente che circola nella spira è:
20 V
DV
is =
=
= 0, 50 A.
R
40 X
6
La corrente che circola nella spira è i s =
2rd ^ d + l h F
2rd ^ d + l h F
DV
ossia
.
=
2
2
R
n0 i f l
n0 i f l
n 0 i f l DV
2
7
2rFd ^ d + l h
= ^ 2 # 10-7 N/A2 h #
^ 10 A h # ^5, 00 # 10-1 m h2 # ^20 V h
= 40 X
^ 5, 0 # 10-4 N h # ^ 1, 0 # 10-3 m h # ^ 5, 01 # 10-1 m h
x 1 - m 1 g - F1 = 0
x 2 - m 2 g - F2 = 0
Il filo è inestensibile e di massa trascurabile, quindi:
x1 = x2
m 1 g + F1 = m 2 g + F2
^ m 1 - m 2 h g = F2 - F1
^m 1 - m 2hg =
n0 l
2rd
2
2
n 0 l^i 2 - i 1h
d=
2r ^ m 1 - m 2 h g
d=
8
^ i 22 - i 21 h
^ 4r # 10-7 N/A2 h # ^ 1, 0 m h # 6^ 196 A h2 - ^ 98 A h2@
= 2, 9 cm .
2r ^ 4 # 10-2 kg - 2 # 10-2 kg h # 9, 8 m/s2
Poiché il cerchione ha resistenza trascurabile, con il collegamento proposto la corrente scorrerà in tutti
i bracci dal centro alla periferia o dalla periferia al centro, a seconda della polarità. L’intensità di corV
rente in ciascun raggio risulta i 0 = 0 .
R
La tensione del filo tende a far girare la ruota in senso orario, quindi, per avere l’equilibrio, il momento della forza magnetica agente sui raggi deve essere orientato in senso opposto. La forza magnetica
v , dove vl è un vettore orientato nel verso della corrente: queapplicata a ciascun braccio è Fv = i vl # B
sta dovrà quindi scorrere dal cerchione verso l’asse della ruota. Quindi il polo della batteria collegato
all’asse dovrà essere quello negativo. Siccome la forza magnetica è uniformemente distribuita, la si può
Idee per insegnare la fisica con
Amaldi L’Amaldi per i licei scientifici © Zanichelli 2012
La riproduzione di questa pagina tramite fotocopia è autorizzata ai soli fini
dell’utilizzo nell’attività didattica degli alunni delle classi che hanno adottato il testo
12
Soluzioni per capitolo
soluzioni degli
esercizi del libro
25
fenomeni magnetici fondamentali
25
considerare applicata nel centro di ciascun raggio, e il modulo del momento magnetico complessivo
1
risulta quindi 4Bli 0 l = 2Bi 0 l2 .
2
Per avere l’equilibrio dovrà quindi essere 2Bi 0 l2 = Mgl, da cui si ricava:
MgR
V0 =
= 0, 167 V .
2Bl
test per l’università
1
A
2
A
prove d’esame all’università
1
2
l
= 13, 6 X
s
1
1
1
= +
= 0, 24 X-1
R eq R R s
V
= 2, 88 A
i =
R eq
V
= 0, 88 A
i =
Rs
Ni
= 27, 6 mT
B = n0
l
R s = N4t
B =
n0 I2 - I1
= 3, 33 # 10-5 T
2 r d/ 2
n I
n
n
I2
2I 1
B1 = 0 1 ; B2 = 0
= 0
2r d 1
2r ^ d - d 1 h 2r ^ d - d 1 h
B1 = B2 "
1
2
d
=
" d 1 = = 0, 04 m
d1 d - d1
3
study abroad
C
Idee per insegnare la fisica con
Amaldi L’Amaldi per i licei scientifici © Zanichelli 2012
La riproduzione di questa pagina tramite fotocopia è autorizzata ai soli fini
dell’utilizzo nell’attività didattica degli alunni delle classi che hanno adottato il testo
13
Soluzioni per capitolo
soluzioni degli
esercizi del libro
1












