Risonanza magnetica
nucleare
Principi fisici
Premessa
●
●
Modello classico
Visualizzazione semplificata
Equazione di moto
Descrizione qualitativa
Modello quantistico
Descrizione accurata
Livelli energetici
Misure quantitative
Momento magnetico
●
●
●
Gli atomi hanno un
momento di spin I
Modello 'trottola'
Il moto rotatorio produce
un momento magnetico
=
M
I
●
Rapporto giromagnetico
Numero di spin
●
●
I è un parametro caratteristico di ogni specie
atomica, può valere 0, 1/2, 1, 3/2, ...
Un atomo con spin I può assumere 2I+1 livelli
energetici, m = I, I-1, ..., -I
/ 2
Elemento:
I
livelli
Ossigeno
0
1
Idrogeno
1/2
2
42.58
1
3
4.31
Azoto
(MHz/T)
-
Situazione a riposo
●
●
Consideriamo un volume contente (anche) atomi
di idrogeno.
I momenti di spin sono orientati in maniera
casuale
●
●
●
Non esiste differenza di energia tra
i vari livelli di spin
I momenti µ hanno tutti la stessa
intensità ma orientazione casuale
La magnetizzazione totale è nulla
Campo magnetico esterno
Applichiamo un forte campo magnetico B0
Allineamento (classico):
Bo
- parallelo a B0
- antiparallelo a B0
Campo magnetico esterno
Applichiamo un forte campo magnetico B0
Allineamento (quantistico):
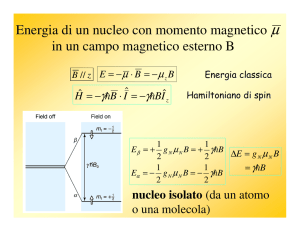
I due livelli di spin hanno energia
diversa (effetto Zeeman)
h
E =−
⋅B0=−z B 0=−
mB
2 i 0
Bo
E =
m i =±
1
2
h
B
2 0
Gli atomi si distribuiscono sui due livelli
N up
E
=exp
N down
KT
Frequenza di Larmor
●
Equazione di moto
d I
=
× B0
dt
Ωo
µ
Bo
d
=
×B 0
dt
In base all'equazione di moto, il
vettore µ ha un moto di
precessione attorno alla
direzione di B0.
La frequenza di precessione è
detta Frequenza di Larmor
=B
Precessione
●
Bo
●
Spin up
Spin down
●
Non si ottiene un
allineamento perfetto
Livelli:
a bassa energia (spin up)
ad alta energia (spin down)
Abbiamo una preponderanza
di atomi nel livello spin up.
Magnetizzazione risultante
y
●
x
z
●
µ
Mzz
Piano xy:
Le orientazioni sono casuali
La risultante è nulla
Asse z:
Nup > Ndown
Mz = (Nup - Ndown) µz
Misurazione M
Mz è un campo magnetico statico, di intensità
inferiore a B0.
Non possiamo misurare direttamente Mz
Occorre quindi introdurre un sistema per generare
un campo magnetico variabile nel tempo
Eccitazione a radiofrequenza
Condizione di risonanza
Applichiamo un campo magnetico rotante
Fotoni di energia
Si ha risonanza se:
h
h=E r f = E = B 0
2
E r f =h
=
B0
2
f =B 0
Applicando un campo magnetico alla frequenza di
Larmor, gli atomi assorbono l'energia elettromagnetica
e passano dalla situazione a spin up alla situazione a
spin down (stato eccitato)
Descrizione macroscopica
z
Bo
y1
Mz
y
x
Ω
B1
x1
Introduciamo un sistema
di riferimento x1, y1, z
rotante a frequenza di
Larmor
Descrizione macroscopica
z
dM
×B1
= M
dt
Bo
Mz
Nel sistema x1 y1 z il momento
Mz e' soggetto ad una rotazione
nel piano zy1 con velocita'
y1
B1
x1
angolare
1=B 1
Se applico B1 per un tempo δt,
il momento Mz ruota di un
angolo
=B 1 t
= flip angle
Descrizione macroscopica
z
Bo
M
a spirale su una superficie
sferica
Mz
y
x
Ω
In riferimento al sistema fisso,
il vettore Mz descrive un moto
B1
Rilassamento
z
Quando rimuoviamo B1 il
Mz
Bo
Mz: componente statica lungo
l'asse z
M
y
x Mxy
sistema torna verso la
condizione di equilibrio
Ω
Mxy: componente nel piano xy
rotante a velocità
Ω
Free Induction Decay
y
Campo magnetico rotante
->radiazione elettromagnetica:
Sinusoide a frequenza di Larmor
Mxy
Free Induction Decay
ω
x
La sinusoide è smorzata e va a zero
in un breve intervallo di tempo
Ampiezza iniziale proporzionale a ρ
Costanti di tempo: T1
z
µz
Bo
y
x µxy
T1: rilassamento
spin-reticolo
Un nucleo 'urta' contro il
reticolo cristallino e torna
nella posizione di
equilibrio
T1 rappresenta la costante di
tempo con cui si ripristina la
componente lungo l'asse z
Costanti di tempo: T2
z
Bo
µxy2
µxy1
x µxy1,2
y
T2: rilassamento
spin-spin
Due nuclei 'urtano' fra di
loro e perdono la
coerenza di fase
T2 rappresenta la costante di
tempo con cui si annulla la
componente xy
Costanti di tempo: T2*
T2*: costante di
tempo misurata
●
●
Il campo magnetico B0
non e' uniforme
La frequenza di Larmor
varia da punto a punto
T2* rappresenta la costante di
tempo con cui si annulla il FID
T1 > T2 > T2*
Equazione di Bloch
dM
×B −R M
−M 0
= M
dt
R=
1
T 2
0
0
0
1
T 2
0
0
0
1
T1
●
Equazione di moto
●
Moto di precessione attorno a B
●
Smorzamento regolato da R
R: Matrice di rilassamento
●
●
Le componenti x e y hanno
costante di tempo T2
La componente z ha costante
di tempo T1
Parametri misurabili
●
●
●
●
T1 e T2 dipendono dallo stato di aggregazione
della materia
T1vuoto > T1gas > T1liquido > T1solido
La misura di T1 e T2 permette di avere
informazioni sui tessuti, differenziando tessuti a
densità simile
Tessuti diversi hanno simile densità protonica
T2* dipende dalla struttura della macchina
Sequenze eccitazione
●
●
●
Il FID contiene informazioni riguardanti ρ, Ω , e T2*
I parametri di interesse sono (principalmente) T1 e
T2
Applicando più eccitazioni α1, α2, .. αn è possibile
stimare i valori di T1 e T2
●
Nell'imaging medico non si usa una eccitazione B1,
ma una sequenza di eccitazione: (α1,t1,α2,t2...)
Gradienti
●
Bo
●
●
Ω
Ω1
Ω
Ω2
●
●
Bo
●
Gx
●
●
Due campioni immersi nel
campo magnetico
I FID hanno la stessa frequenza
Non posso distinguerli
Campo magnetico B=B0+Gx x
Ω1 = B0 + Gx x1
Ω2 = B0 + Gx x2
FID a frequenza diversa
Separo i due campioni con
un'analisi in frequenza
Componenti hardware