PROVA SCRITTA DI ELETTROTECNICA

PROVA SCRITTA DI ELETTROTECNICA
Ing. Aeronautica, Ing. Chimica, Ing. Nucleare, Ing. dei Materiali
COMPITO N.2
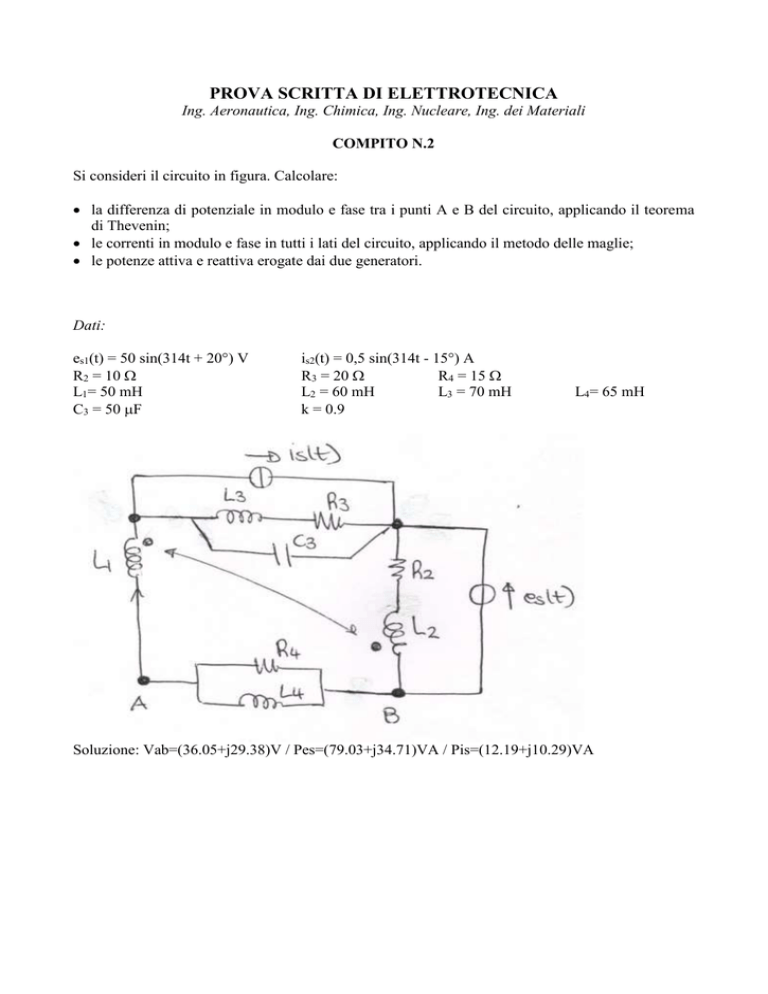
Si consideri il circuito in figura. Calcolare:
 la differenza di potenziale in modulo e fase tra i punti A e B del circuito, applicando il teorema
di Thevenin;
 le correnti in modulo e fase in tutti i lati del circuito, applicando il metodo delle maglie;
 le potenze attiva e reattiva erogate dai due generatori.
Dati:
es1(t) = 50 sin(314t + 20°) V
R2 = 10 
L1= 50 mH
C3 = 50 F
is2(t) = 0,5 sin(314t - 15°) A
R3 = 20 
R4 = 15 
L2 = 60 mH
L3 = 70 mH
k = 0.9
L4= 65 mH
Soluzione: Vab=(36.05+j29.38)V / Pes=(79.03+j34.71)VA / Pis=(12.19+j10.29)VA
ESONERO DALLA PROVA SCRITTA
ELETTROTECNICA
Ing. Aerospaziale
(13/05/1998)
COMPITO N.1
Si consideri il sistema trifase simmetrico equilibrato rappresentato in figura mediante lo schema
equivalente unifilare. La tensione concatenata in D è VD=380 V. La caduta di tensione percentuale
sul trasformatore T2 è dell' 1.53%.
Determinare:
1. il circuito equivalente monofase;
2. le correnti nei carichi in modulo e fase;
3. la capacità del banco di condensatori a stella da inserire in derivazione alla sbarra B per ridurre la
caduta di tensione percentuale sul trasformatore T1 del 5% del suo valore (si supponga costante
la tensione in B prima e dopo il rifasamento).
Dati:
T1:
T2:
T3:
k1=150000/30000
k2=30000/400
k3=30000/3000
Pn1 = 500 kVA
Pn2 = 80kVA
Pn3 = 50 kVA
C1:
C2:
C3:
C4:
380 V
380 V
30000 V
3000 V
10 kW
15 kVA
100 kVA
50 kW
L1:
L2:
l1 = 10 km
l2 = 1 km
R1 = 0.5 /km
R2 = 0.3 /km
Pcc1%=2%
Pcc2%=3%
Pcc3%=3%
Vcc1%=7%
Vcc2%=5%
Vcc3%=6%
cos1 = 0.8
8 kVAR
60 kW
50 kVAR
X1 = 2 /km
X2 = 1 /km
Soluzione: I1=(15.24-j11.43)A / I2=(19.34-j12.19)A / I3=(1.13-j1.49)A / I4=(8.42-j8.75)A
C=0.33μF
ESONERO DALLA PROVA SCRITTA
ELETTROTECNICA
Ing. Aerospaziale
(13/05/1998)
COMPITO N.2
Si consideri il sistema trifase simmetrico equilibrato rappresentato in figura mediante lo schema
equivalente unifilare. La tensione concatenata in D è VD=3 kV. Le perdite per effetto Joule sul
trasformatore T1 sono di 1849 W.
Determinare:
1. il circuito equivalente monofase;
2. le correnti nei carichi in modulo e fase;
3. la capacità del banco di condensatori a triangolo da inserire in derivazione alla sbarra B per
ottenere un fattore di potenza di 0.9 (si supponga costante la tensione in B prima e dopo il
rifasamento).
Dati:
T1:
T2:
k1=50000/3000
k2=50000/1000
Pn1 = 200 kVA
Pn2 = 100 kVA
Pcc1%=?
Pcc2%=2.5%
C1:
C2:
C3:
C4:
1000 V
1000 V
50 kV
3000 V
40 kW
60 kVA
100 kW
30 kVAR
L1:
L2:
L3:
l1 = 10 km
l2 = 10 km
l3 = 500 m
R1 = 10 /km
X1 = 50 /km
R2 = 10 /km
X2 = 50 /km
R3 = 0.7 /kmX3 = 2 /km
Vcc1%=6%
Vcc2%=5%
50 kVAR
cos2 = 0.8
cos3 = 0.9
cos4 = 0.9
Soluzione: I1=(4.06-j3.7)A / I2=(4.55-j2.4)A / I3=(196.38-j53.79)A / I4=(23.44-j11.68)A
C=0.24μF
ESONERO DALLA PROVA SCRITTA
ELETTROTECNICA
Ing. Aerospaziale
(13/05/1998)
COMPITO N.3
Si consideri il circuito schematizzato in figura. Calcolare la differenza di potenziale tra i punti A,B
applicando il teorema di Thevenin. Determinare quindi le correnti I 1, I 2, la potenza reattiva
associata al condensatore C1 e la potenza complessa associata al generatore di tensione.
Dati:
is1(t) = 1 sin(314t - /6) A
is3(t) = 0,5 sin(314t - /2) A
R1 = 50 
L1= 100 mH
M = 60 mH
es2(t) = 200 sin(314t + /4) V
R3 = 60 
L2 = 120 mH
C1 = 50 F
R4 = 45 
L3 = 80 mH
L4= 90 mH
Soluzione: Vab=(3.15+j7.46)V / I1=(-0.701-j0.086)A / I2=(3-j2.61)A / Qc=11.05VAR
P=(-39-j561)VA
PROVA SCRITTA DI ELETTROTECNICA
Ing. Aerospaziale
(13/07/1998)
Si consideri il circuito schematizzato in figura. Calcolare le potenze attiva e reattiva associate ai
generatori di tensione e di corrente. Calcolare inoltre le correnti I 1, I 2.
Dati:
R1 = 50 
L1= 90 mH
C2 = 10 F
I s1 = 2 j 0,5 A
E s3 = 100 + j 100 V
R2 = 40 
L2 = 60 mH
C3 = 30 F
I s2 = 1 +j 1,5 A
R3 = 60 
L3 = 80 mH
 = 314 rad/s
I s4 = 1.2 j 2,1 A
M = 30 mH
Soluzione: Pis1=(-21.93+j215.2)VA / Pis2=(119.88-j0.94)VA / Pes3=(571+j99)VA
Pis4=(423.58+j177.9)VA / I1=(0.24+j0.302)A / I2=(-0.61+j0.55)A
PROVA SCRITTA DI ELETTROTECNICA
Ing. Aerospaziale
(21/10/1998)
Si consideri il sistema trifase simmetrico equilibrato rappresentato in figura mediante lo schema
equivalente unifilare. La tensione concatenata in B è VB=10 kV.
Determinare:
1. il circuito equivalente monofase;
2. le correnti nei carichi in modulo e fase;
3. la caduta di tensione percentuale sul trasformatore T2;
4. la capacità del banco di condensatori a triangolo da inserire in derivazione alla sbarra E affinchè
la caduta di tensione percentuale sul trasformatore T1 e sulla linea L, tra le sbarre A ed E, non
superi il 3% (si supponga costante la tensione in E prima e dopo il rifasamento).
Dati:
T1:
T2:
k1=10000/380
k2=10000/3000
Pn1 = 20 kVA
Pn2 = 50 kVA
C1:
C2:
C3:
C4:
C5:
380 V
380 V
10000 V
3000 V
3000 V
6 kW
13 kVA
50 kVA
25 kVA
19 kW
L:
l = 500 m
RL = 0,1 /km
Pcc1%=3%
Pcc2%=3%
Vcc1%=5%
Vcc2%=6%
cos1 = 0,85
9 kVAR
35 kW
cos4 = 0,8
16 kVAR
XL = 0,4 /km
Soluzione: I1=(8.63-j2.34)A / I2=(13.45-j13.18)A / I3=(2.02-j2.06)A / I4=(3.99-j3.12)A
I5=(3.78-j3.32)A / ΔV%=5.44% / C=65.96μF