politecnico di bari - Istituto Nazionale di Fisica Nucleare

POLITECNICO DI BARI
DIPARTIMENTO DI
INGEGNERIA ELETTRICA E DELL’INFORMAZIONE
Corso di Laurea Triennale in Ingegneria Elettronica e delle
Telecomunicazioni
TESI DI LAUREA
in
FONDAMENTI DI OPTOELETTRONICA
INVESTIGAZIONE TEORICO-SPERIMENTALE DI UN
SISTEMA OPTOELETTRONICO DI DISTRIBUZIONE DI
CLOCK PER L’ESPERIMENTO TOTEM ALL’LHC DEL
CERN
Relatore:
Chiar.mo Prof. Ing. Vittorio PASSARO
Correlatori:
Dott. Francesco S. CAFAGNA
Dott. Emilio RADICIONI
Laureando:
Andrea GIANNINI
ANNO ACCADEMICO 2014 - 2015
Sommario
Introduzione ................................................................................................................................................ 2
Capitolo 1 ...................................................................................................................................................... 4
Large Hadron Collider ......................................................................................................................... 4
L’esperimento TOTEM ........................................................................................................................ 6
Sistema optoelettronico di distribuzione di clock ................................................................. 10
Capitolo 2 ................................................................................................................................................... 15
Sistemi di comunicazione ottici .................................................................................................... 15
Lightwave Systems ............................................................................................................................ 15
Limitazioni dovute all’attenuazione delle fibre ottiche ...................................................... 21
Dispersione in fibra ottica .............................................................................................................. 26
Capitolo 3 ................................................................................................................................................... 34
Sistemi Wavelength Division Multiplexing .............................................................................. 34
Analisi e caratterizzazione di alcuni componenti di un sistema DWDM ...................... 37
Sorgente laser ................................................................................................................................. 37
Isolatore ottico ............................................................................................................................... 42
Circolatore........................................................................................................................................ 45
Multiplexer a Demultiplexer ..................................................................................................... 49
Add-drop multiplexer .................................................................................................................. 52
Fiber Bragg Gratings .................................................................................................................... 55
Capitolo 4 ................................................................................................................................................... 57
Mach Zehnder modulator ............................................................................................................... 57
Analisi di alcune caratteristiche del Mach Zehnder modulator ....................................... 60
Conclusioni ................................................................................................................................................ 66
1
Introduzione
Il continuo aumento dell’energia sprigionata dalle collisioni di protoni dell’LHC, la
riduzione della distanza temporale tra i pacchetti di protoni che compongono i fasci
che viaggiano nella beam pipe, insieme all’aumento nella popolazione di protoni per
gruppo, pone nuovi quesiti sul futuro della ricerca nei vari campi della fisica, ma
richiede anche nuovi apparati tecnologici all’avanguardia.
Tra gli esperimenti di maggior importanza si inserisce il TOTEM Experiment,
che ha come obiettivo la misura la sezione d’urto totale protone-protone alle energie
dell’LHC, lo studio dello scattering elastico p-p e gli eventi diffrattivi.
La Collaborazione ha approvato un aggiornamento dell’esperimento TOTEM,
finalizzato ad una maggiore precisione nello studio dei processi così detti diffrattivi.
Per ottenere gli obiettivi richiesti, è necessario conoscere il momento di arrivo di ogni
traccia passante attraverso le Roman Pot. Per fare questo è necessario installare dei
rivelatori in grado di fornire l’istante esatto del passaggio della particella, in modo da
associarla ad un vertice di interazione ricostruito dall’esperimento CMS. Per far questo
è necessario che il rivelatore abbia una risoluzione temporale di ∼50 𝑝𝑠. Naturalmente,
una tale precisione, da realizzarsi in rivelatori distanti oltre 200 𝑚 dalla sorgente,
richiede una distribuzione del segnale di sincronizzazione (clock) in grado di garantire
alti livelli di precisione e bassissimi valori di jitter temporale.
Il presente lavoro di tesi è volto all’analisi teorico-sperimentale dei principali
elementi del sistema optoelettronico di distribuzione di clock.
Nel primo capitolo viene data una breve descrizione dell’LHC del CERN,
introducendo i principali esperimenti previsti in ogni punto di interazione, tra cui si
inserisce l’esperimento TOTEM. In seguito vengono descritti gli obiettivi
dell’esperimento, insieme alla descrizione dei rivelatori necessari al conseguimento
degli obiettivi proposti. Nella terza parte del capitolo, viene descritto il sistema di
distribuzione di clock, con particolare riferimento alle unità che compongono il
sistema.
Il secondo capitolo tratta dei sistemi di comunicazione ottici, introducendo i
principali tipi di architetture di sistema. In seguito vengono descritti i principali fattori
di perdita di un sistema di trasmissione in fibra ottica.
2
Nel terzo capitolo vengono spiegate le principali caratteristiche di un sistema
WDM. Vengono poi descritti e caratterizzati i principali componenti del sistema di
distribuzione di clock per l’esperimento TOTEM.
Il quarto capitolo riguarda l’analisi di alcune caratteristiche del modulatore
ottico scelto per il sistema di clock, analizzando i problemi principali legati alla
polarizzazione di tale dispositivo. In seguito viene proposta una possibile soluzione,
sostenuta da prove sperimentali.
3
Capitolo 1
Large Hadron Collider
Il Large Hadron Collider (LHC), è il più grande e il più potente acceleratore di particelle
mai costruito. Si trova presso l’ European Organization for Nuclear Research (CERN),
fondata nel 1954 al confine tra Francia e Svizzera, vicino alla città di Ginevra.
I principali campi di ricerca, intrapresi al CERN, hanno come obiettivo principale
la ricerca sperimentale nell’ambito della fisica delle particelle elementari, nonché lo
studio delle forze fondamentali che compongono la materia e delle interazioni ad esse
legate.
L’LHC è situato in un tunnel di circa 26,3 𝑘𝑚 di circonferenza, posto a circa
100 𝑚 di profondità. È nato nel 1994 per sostituire il precedente Large Electron
Positron (LEP) Collider, spento nel 2000. Il nuovo acceleratore è stato messo in funzione
per la prima volta nel settembre del 2008.
L’LHC è un acceleratore di particelle formato da due anelli, in cui viaggiano protoni o
ioni pesanti. Per trasferire loro l’energia necessaria, le particelle passano attraverso
una serie di acceleratori, che, ad ogni passaggio, aumentano la loro energia fino a
raggiungere quella necessaria per essere iniettate nell’LHC per l’accelerazione finale.
In particolare, le particelle passano prima attraverso il Linear Paricle Accelerator
(LINAC), a cui segue il BOOSTER, il Proton Synchroton (PS) e il Super Proton Synchroton
(SPS). In questo modo le particelle riescono ad essere accelerate fino ad energie di 450
GeV.
Dal SPS quest’ultimo, due fasci di particelle vengono estratti ed iniettati negli
anelli dell’LHC, per l’accelerazione finale che può portare le particelle ad una energia
massima di 7 𝑇𝑒𝑉. I fasci di particelle, così accelerati, vengono compressi in pacchetti
e portati a collidere in quattro punti di interazione (interaction points, IP), in modo da
sfruttare l’urto della interazione per raggiungere un massimo di 14 𝑇𝑒𝑉 di energia
disponibile per collisione. All’energia massima di accelerazione, le particelle
4
raggiungono una velocità di circa 0,999999991𝑐, ovvero circa tre metri al secondo più
lenti della velocità della luce.
In ogni punto di interazione, sono stati previsti degli esperimenti, tra questi i
principali sono: ALICE ,ATLAS, CMS, LHCb, TOTEM ed LHCf.
FIGURA 1
L’obiettivo principale dell’esperimento ATLAS (A Toroidal LHC Apparatus) e
dell’esperimento CMS (Compact Muon Solenoid) è la ricerca del bosone di Higgs,
particella teorizzata nel così detto Modello Standard. Questa particella è stata rivelata
nel 2012, dai due esperimenti suddetti, , confermando le previsioni del modello.
L’esperimento ALICE (A Large Ion Collider Experiment) è stato progettato per
studiare lo stato della materia detto quark-gluon plasma, uno stato in cui si sarebbe
dovuta trovare la materia nei primi istanti della nascita dell‘Universo.
Con LHCb (Large Hadron Collider beauty) si vuole studiare nel dettaglio il
decadimento di particelle contenenti quark bottom, alla ricerca di eventi rari che
5
spieghino il perché della asimmetria cosmologica tra materia e antimateria
nell’Universo.
Large Hadron Collider forward (LHCf) e TOTal cross section, Elastic scattering
and diffraction dissociation Measurement (TOTEM) sono esperimenti dedicati
specificatamente allo studio dei processi che si verificano nelle interazioni associate
alla produzione della maggior parte delle particelle secondarie, nella ragione in avanti,
la cosiddetta regione Forward.
L’esperimento TOTEM
L’obiettivo principale dell’esperimento TOTEM, è quello di rivelare le particelle che
emergono, dall’interaction point, con piccoli angoli rispetto all’asse del fascio, al fine di
misurare la sezione d’urto totale protone-protone alle energie dell’LHC, e di studiare lo
scattering elastico p-p e gli eventi diffrattivi.
Grazie all’utilizzo di tre tipi di rivelatori disposti simmetricamente rispetto
all’interaction point, è possibile coprire intervalli di pseudo-rapidity ,non coperti da
altri rivelatori, un fattore che dà informazioni sull’angolo che si forma tra la particella
diffratta e il fascio di particelle principale. A seconda della posizione e delle accettanza
geometrica dei tre tipi di rivelatori, ciascun detector è in grado di ricoprire un diverso
intervallo di pseudo-rapidity.
Inoltre sono previste delle campagne di prese dati assieme a CMS, in modo da
ottenere la copertura di una regione di pesudo-rapidità, mai raggiunta in precedenza.
TOTEM è stato progettato per sfruttare al meglio il focheggiamento dei magneti di LHC.
In particolari condizioni dell’ottica magnetica e della intensità del fascio, l’accettanza
dei rivelatori di TOTEM diventa massima, per determinate topologie di evento. Queste
condizioni di fascio, vengono realizzate appositamente per TOTEM, in brevi periodi
dell’anno, dedicando completamente la presa dati a questo esperimento. Si rende
quindi necessario sfruttare al massimo i brevi periodi di presa dati concessi, rendendo
il più efficiente e veloce possibile la presa dati dell’esperimento.
6
Come detto in precedenza, l’esperimento TOTEM utilizza tre tipi di rivelatori: due
telescopi 𝑇1 e 𝑇2 posizionati rispettivamente a 9 𝑚 e a 13 𝑚 dal punto di interazione,
e delle Roman Pots (RP). Queste sono state posizionate in un primo tempo a 147 𝑚 e
220 𝑚 dall’IP, ed in seguito ricollocate a 210m e 200m dall’IP. I telescopi sono rivelatori
a gas utilizzati per rivelare particelle che subiscono fenomeni di interazione inelastica
ad alti valori di pseudo-rapidity. Al contrario le Roman Pots, permettono di rivelare
particelle che emergono con angoli molto piccoli rispetto alla direzione di
propagazione del fascio principale, grazie all’utilizzo di rivelatori particolari, formati
da piani di silicio disegnati in modo tale da presentare la massima superficie sensibile
possibile, all’ avvicinarsi verso il fascio.
FIGURA 2
Il telescopio 𝑇1 è formato da due bracci a forma conica; posizionati all’interno
dell’esperimento CMS, a distanza di 9 𝑚 dall’IP. Ha un ruolo importante nel
determinare il vertice del punto di interazione e nel produrre segnali di trigger
utilizzati per discriminare le interazioni che hanno un vertice nel IP. Il detector è
formato da Cathode Strip Chambers (CSC) di forma trapezoidale e di grandezza diversa.
Gruppi di sei camere, formano una struttura ad anello intorno al fascio in un piano
perpendicolare ad esso. Ciascun ramo del telescopio è formato da cinque di questi piani
disposti in modo da mantenere la stessa distanza fra di loro, dove il più piccolo è quello
più vicino all’interaction point.
7
FIGURA 3
Anche il tescopio 𝑇2è formato da due bracci posizionati a distanza di 13,5 𝑚 dal punto
di interazione. Questi detector permettono lo studio di eventi diffrattivi, e sono
rivelatori basati sulla tecnologia Triple-Gas Electron Multiplier (GEM).
Le camere GEMs sono formate da fogli di polimeri spessi 50 µ𝑚 ricoperti di uno
strato di 5 µ𝑚 di rame da entrambi i lati. È possibile praticare buchi di 70 µ𝑚 di
diametro, distanziati tra loro di 140 µ𝑚, in modo tale da ottenere elevati valori di
campo elettrico in questi buchi e in modo da accelerare, al loro interno, gli elettroni
rilasciati nel gas da radiazioni ionizzanti. Grazie a questo meccanismo di accelerazione,
si riescono ad ottenere elevati valori di guadagno utilizzando tre fogli GEM a distanza
di 2 𝑚𝑚 l’uno dall’altro.
Le camere di 𝑇2 hanno forma semicircolare, con raggio interno posto verso il
beam pipe. Un quarto del telescopio è formato da 10 camere GEM; un braccio di T2 è
formato da 20 camere disposte in modo simmetrico rispetto al fascio, in modo da
ottenere una completa copertura nell’angolo azimutale nella rivelazione delle
particelle.
8
FIGURA 4
I Roman Pot sono dispositivi che permettono l’inserimento di rivelatori, nel tubo del
fascio di LHC. I rivelatori sono disposti in una camera inserita nel vuoto secondario del
fascio, un meccanismo motorizzato, permette di portare lentamente i rivelatori
all’interno della camera, al fine di avvicinarli il più possibile al tubo di vuoto primaio in
cui circola il fascio. Questo permette di rivelare particelle diffratte con angoli molto
piccoli rispetto alla direzione del fascio.
Grazie a questo meccanismo, è possibile riuscire ad avvicinare i rivelatori fino a 1 𝑚𝑚
di distanza dal fascio con una precisione di 10 µ𝑚.
Ciascun detector è formato da un piano di silicio spesso 300 µ𝑚. Dieci piani di
silicio formano un package, che viene inserito nella camera suddetta. La lettura della
carica rilasciata dalle particelle ionizzanti, viene effettuata attraverso strisce
depositate sul silicio; la geometria delle strisce e tale da minimizzare gli spazi morti
nella zone più vicina al fascio.
I 10 piani sono suddivisi in due gruppi da 5 orientati a ±45° rispetto al bordo più vicino
al fascio. Questo permette di ricostruire la direzione della particella, sfruttando le
informazioni delle due proiezioni spaziali..
Il movimento del package nelle Pot, avviene grazie ad un motore passo-passo che lo
avvicina al fondo della Pot. Tre Roman Pot formano una unit. in cui, due Pot sono
montate verticalmente rispetto al piano dell’acceleratore, mentre la terza è disposta
orizzontalmente. Due unit a distanza di 5 𝑚 formano una station. Durante la prima fase
di attività di LHC, un totale di 4 station sono state installate rispettivamente a ±147m e
±220m dal IP. In seguito le stazioni a ±147m sono state ricollocate ad una distanza di
9
±210m e quattro nuove pot orizzontali, due per ogni lato, sono state installate tra la
stazioni a ±220m.
Sistema optoelettronico di distribuzione di clock
Il sistema di distribuzione di clock scelto al fine di garantire alti livelli di precisione e
bassissimi valori di jitter temporale, è un sistema di tipo Dense Wavelength Division
Multiplexer (DWDM), forma di multiplazione a divisione di frequenza che verrà
approfondita nel terzo capitolo di questa tesi.
Il sistema richiede la distribuzione di due segnali di clock di riferimento inviati dalla
counting room a dei ricevitori disposti simmetricamente rispetto all’interaction point,
lungo l’LHC; a questi si aggiunge un terzo segnale che viaggia sulla stessa fibra ottica,
necessario per correggere i ritardi introdotti dal sistema di trasmissione ottico. Si può
suddividere il sistema in quattro unità principali: Transmission Unit, Distribution Unit,
Measurement Unit e Receiving Unit.
FIGURA 5
Nell’unità di trasmissione vengono generate due portanti ottiche da sorgenti laser
DWDM alle lunghezze d’onda centrali del canale 𝐼𝑇𝑈32 e 𝐼𝑇𝑈34 , rispettivamente
𝜆𝐶𝐻32 = 1551,72 𝑛𝑚 e 𝜆𝐶𝐻34 = 1550,12 𝑛𝑚 . I segnali passano attraverso degli
isolatori ottici, che proteggono la sorgente da eventuali riflessioni provenienti dai
10
dispositivi successivi. I segnali di riferimento modulano le portanti ottiche mediante
un modulatore Mach Zehnder, che effettua una modulazione indiretta dei segnali in
uscita dalle sorgenti DWDM. A seguire, i segnali ottici vengono multiplati in un’unica
fibra ottica. Il segnale multiplato viene poi inviato all’unità di distribuzione.
FIGURA 6
Dall’unità di trasmissione, per compensare l’attenuazione introdotta dal multiplexer
ottico e dal seguente splitter dell’unità di distribuzione, è necessario un amplificatore
ottico Erbium-Doped Fiber Amplifier (EDFA). In seguito il segnale viene splittato in
quattro segnali multiplati da uno splitter ottico, che verranno trasmessi alle quattro
unità riceventi. Al segnale multiplato, va però aggiunto il terzo segnale di controllo
inviato dall’unità di misura.
FIGURA 7
11
In questa unità, viene generato un segnale di riferimento che permette di quantificare
e correggere i ritardi introdotti dal sistema in fibra ottica. Una sorgente laser DWDM
genera il terzo segnale di lunghezza d’onda corrispondente a quella centrale del canale
𝐼𝑇𝑈36, 𝜆𝐶𝐻36 = 1548,51 𝑛𝑚. Anche in questo caso, la portante ottica generata passa
attraverso un isolatore ottico, e in seguito va in ingresso ad un modulatore ottico Mach
Zehnder. Il segnale di controllo viene generato da un Network Analyzer e mandato a
modulare la portante ottica. Quest’ultima viene inviata attraverso uno switch ottico, a
ciascuna unità di ricezione e ad un riflettore, utilizzato per la calibrazione. Il segnale
della portante di riferimento viene aggiunto ad ognuno dei quattro segnali multiplati
in uscita dallo splitter ottico grazie all’utilizzo di Add-Drop multiplexer. Il segnale
multiplato che ora trasporta l’informazione spettrale relativa alle tre portanti ottiche
modulate, viene trasmesso alle unità di ricezione poste nel tunnel a 220 𝑚 e 210 𝑚. Il
segnale di ritorno dalle unità di ricezione passa attraverso lo switch ottico e poi va in
ingresso alla porta 2 di un circolatore ottico che trasmette il segnale riflesso verso uno
strumento di misura. Un network analizer confronta la fase del segnale riflesso
ricevuto con il segnale di riferimento, in modo da ottenere informazioni sul ritardo che
risente il segnale passando attraverso ciascun canale di distribuzione.
FIGURA 8
Ciascun uscita degli add-drop multiplexer della measurement unit va in ingresso al
Fiber Bragg Grating (FBG) in ognuna unità di ricezione. Il FBG non fa altro che riflettere
la portante modulata dall’unità di misura. In ingresso al demultiplexer posto in cascata
12
al reticolo di Bragg, arriverà un segnale multiplato formato dalle portanti modulate
corrispondenti alle lunghezze d’onda 𝜆𝐶𝐻32 e 𝜆𝐶𝐻34 . Il demultiplexer separa le
lunghezze d’onda del segnale multiplato su due fibre distinte poste in uscita dal
dispositivo. Infine i due segnali vengono demodulati da due fotorivelatori in ciascuna
unità di ricezione.
13
14
Capitolo 2
Sistemi di comunicazione ottici
Grazie alle caratteristiche di funzionamento delle fibre ottiche come mezzo di
propagazione guidata di campi elettromagnetici, si riesce ad ottenere una condizione
di trasferimento di potenza quasi perfetta tra ingresso e uscita di un sistema di
comunicazione ottico. Si noti che grazie alla condizione di Total Internal Reflection
(TIR) la potenza ottica incidente all’interfaccia core-cladding viene completamente
riflessa lungo la linea, facendo in modo che i raggi incidenti con angolo maggiore
dell’angolo critico rimangano intrappolati nel nucleo. Perciò le fibre ottiche si
comportano da mezzo di trasmissione praticamente perfetto. Vedremo che a causa di
meccanismi di perdita caratteristici di tali sistemi, si perde questa condizione ideale.
Inoltre, un sistema di trasmissione in fibra è immune a interferenza elettromagnetica,
è caratterizzato da bassissimi valori di Bit Error Rate (BER) e permette di ottenere
velocità di trasmissione dell’informazione non ottenibili con un sistema in cavo
coassiale. Questi ed altri vantaggi hanno portato alla nascita di sistemi di
comunicazione ottici, di cui si parlerà nel seguente capitolo.
Lightwave Systems
Un Lightwave System è un sistema di comunicazione in fibra ottica, composto da un
trasmettitore ottico, un canale di trasmissione in fibra ottica e un ricevitore ottico. È
possibile suddividere questi sistemi di trasmissione in tre grandi categorie, a seconda
del tipo di architettura: point-to-point links, distribution networks e local-area networks.
15
FIGURA 9
Il compito di un collegamento point-to-point è quello di trasportare informazioni, in
forma di sequenza di bit, tra due sistemi in comunicazione, garantendo la massima
accuratezza possibile. A seconda delle applicazioni, la lunghezza dei collegamenti può
variare da meno di un chilometro a migliaia di chilometri. Ad esempio, spesso si sfrutta
l’immunità da interferenze elettromagnetiche dei collegamenti per mettere in
comunicazione più terminali non a grande distanza reciproca. In questi casi non sono
di primaria importanza i bassi valori di perdita e la larga banda delle fibre ottiche. Al
contrario, queste ultime due caratteristiche sono da tenere in conto in un sistema ottico
per collegamenti transoceanici, dove un collegamento in fibra permette di ridurre i
costi operativi. Se la lunghezza del collegamento supera di circa 20-100 𝑘𝑚 una certa
distanza prefissata di progetto, che varia a seconda della lunghezza d’onda utilizzata, è
necessario compensare le perdite in fibra affinché il segnale ricevuto sia rilevabile. Fino
al 1990 si sono utilizzati dei rigeneratori optoelettronici che rivelano il segnale ottico
ricevuto e lo convertono in una sequenza di bit che modula una sorgente ottica. Oggi
si utilizzano maggiormente gli amplificatori ottici, che permettono di amplificare
direttamente il segnale ottico evitando la conversione in segnale elettrico. Bisogna
considerare che questi ultimi aggiungono rumore, peggiorando gli effetti di
dispersione in fibra, perciò in alcuni casi è necessario ricorrere ad alcune tecniche di
compensazione degli effetti dispersivi. I ripetitori optoelettronici, siccome rigenerano
la sequenza di bit originaria, non causano complicazioni di questo tipo.
Un parametro di merito di questi sistemi è il bit rate-distance product BL, dove
L è la distanza tra i rigeneratori optoelettronici o tra gli amplificatori ottici. BL dipende
dalla lunghezza d’onda operativa, siccome sia il fenomeno della dispersione in fibra
ottica che il fenomeno dell’attenuazione introdotta dalle fibre dipendono da essa.
16
I sistemi point-to-point moderni che funzionano a grandi distanze, utilizzano
entrambi i tipi di dispositivi considerando un rigeneratore optoelettronico dopo una
serie di amplificatori ottici, in modo da compensare il rumore introdotto da questi
ultimi. Quello che si vorrebbe ottenere è un sistema di trasmissione dotato di
rigeneratori di segnale che funzionino nel dominio delle frequenze ottiche senza
convertire il segnale ricevuto in un segnale elettrico di frequenza molto più bassa.
Spesso si richiede ad un sistema di trasmissione in fibra ottica, che il segnale che
trasporta informazione non venga trasmesso tra due sistemi in comunicazione, ma che
venga distribuito verso più utenti; ad esempio questo accade nei sistemi di
distribuzione di servizi telefonici e nella trasmissione multicanale della TV via cavo. In
questo caso si parla di distribution networks, e le distanze sono in media minori di 50
𝑘𝑚.
FIGURA 10
Si parla di hub topology quando ciascun utente è connesso ad un nodo principale (hub)
posto al centro del sistema di trasmissione. Come nel i sistemi point-to-point, bisogna
tenere in conto sia dei fenomeni di dispersione, sia dei fenomeni di attenuazione, anche
se in minor misura grazie alle distanze ridotte dei network di distribuzione. Il
principale problema di un sistema di quest’ultima tipologia, è che il fuori servizio di
una singola fibra può compromettere gran parte del sistema di trasmissione, perciò
spesso si utilizzano dei sistemi point-to-point aggiuntivi per connettere insieme gli hub
più importanti.
17
FIGURA 11
Si parla di bus topology, quando è una singola fibra ottica a trasportare il segnale
multicanale attraverso l’area di servizio. Ciascun utente preleva una frazione del
segnale trasmesso utilizzando degli accoppiatori. Grazie alla larga banda delle fibre
rispetto
alla
banda
di
un
cavo
coassiale,
si
riescono
a
trasmettere
contemporaneamente più di 100 canali su una stessa fibra ottica. Un inconveniente di
questa tipologia è l’alto contributo di perdite di segnale che cresce esponenzialmente
con il numero di collegamenti accoppiati. Infatti, se indichiamo con 𝑃𝑇 la totale potenza
trasmessa, 𝐶 il fattore di accoppiamento dell’accoppiatore, e δ un fattore che tiene
conto delle perdite di inserzione, si ha:
𝑃𝑅,1 = 𝑃𝑇 𝐶
𝑃𝑇,1 = 𝑃𝑇 (1 − 𝐶)(1 − 𝛿)
𝑃𝑅,2 = 𝑃𝑇 𝐶(1 − 𝐶)(1 − 𝛿),
dove 𝑃𝑇,1 è la quantità di potenza trasmessa in fibra dopo la porta 1 e 𝑃𝑅,2 è la potenza
disponibile alla porta 2 (Figura 11). Di conseguenza la potenza disponibile alla porta 𝑁
sarà:
𝑃𝑅,𝑁 = 𝑃𝑇 𝐶[(1 − 𝛿)(1 − 𝐶)]𝑁−1
18
Trascurando gli effetti di dispersione, si potrebbero porre lungo la tratta degli
amplificatori ottici al fine di incrementare la potenza del segnale che viaggia lungo la
fibra in modo da rendere disponibile l’informazione ad un numero elevato di utenti.
Spesso nasce la necessità di avere più utenti connessi contemporaneamente in un’area
limitata, in modo da permettere a ciascuno di accedere alla rete in modo casuale e di
trasmettere informazioni ad un qualsiasi altro utente connesso. In questo caso si parla
di local-area networks (LANs). Siccome le distanze tra sistema in trasmissione e sistema
in ricezione sono minori di 10 𝑘𝑚, il fenomeno di perdita delle fibre ottiche non causa
grossi problemi in questi sistemi di trasmissione, permettendo di sfruttare al meglio la
larga banda caratteristica di un sistema di comunicazione in fibra. La sostanziale
differenza tra una local-area network e una distribution network di topologia hub sta
nel fatto che quest’ultimo tipo di architettura di sistema non permette un accesso
casuale alla rete. Si utilizzano diverse topologie di sistema a seconda delle connessioni
tra i diversi elementi che compongono la rete.
È possibile anche con questo tipo di architettura di sistema, implementare una
bus topology, un esempio sono le reti Ethernet. In quest’ultimo caso si preferisce far uso
ancora di collegamenti in cavo coassiale, a causa degli eccessivi valori di perdita che
nascono in corrispondenza di ogni collegamento e che limitano il numero di utenti
connessi, come accade nella tipologia bus delle reti di distribuzione in fibra ottica.
19
FIGURA 12
Invece, nella ring topology ciascun nodo è connesso al nodo adiacente tramite un
collegamento di tipo point-to-point fino a formare un anello. Ciascun nodo utilizza un
trasmettitore e un ricevitore per comunicare in rete, e può funzionare da ripetitore. Lo
scambio di informazioni avviene all’interno di un sistema di tipo token ring, nel quale
un particolare tipo di messaggio all’interno dell’anello stabilisce quale dei nodi della
rete può trasmettere informazioni e quale nodo può ricevere dati. Un esempio in fibra
ottica è il Fiber Distributed Data Interface (FDDI) che permette di ottenere una velocità
di trasmissione di 100 𝑀𝑏/𝑠 , utilizzando fibre multimodali con sorgenti di
trasmissione di tipo light-emitting diodes (LEDs) per connessioni all’interno di uno
stesso edificio e fibre monomodali che utilizzano sorgenti laser per trasmettere
informazioni tra edifici diversi; questo è dovuto al fatto che l’utilizzo di fibre
multimodali permette la contemporanea presenza di più modi propagativi all’interno
della fibra, sebbene limiti la distanza dei collegamenti e la banda utile, a causa del
fenomeno della dispersione modale delle fibre ottiche.
Per quanto riguarda la star topology, tutti i nodi della rete sono connessi ad un
nodo centrale, chiamato star o hub, tramite collegamenti di tipo point-to-point. Se il
nodo centrale è un dispositivo attivo, allora si parla di active-star network. In questo
20
caso i segnali ottici ricevuti vengono convertiti in segnali elettrici attraverso dei
ricevitori ottici, e la distribuzione dei segnali avviene nel dominio elettrico. Al
contrario, se il nodo centrale è un dispositivo passivo, la distribuzione avviene nel
dominio ottico, utilizzando accoppiatori direzionali. In questo caso si parla di passivestar networks. Allo stesso modo della bus topology distribution network, anche in
quest’ultimo caso il numero di utenti connessi limita la totale potenza trasmessa alla
generica porta di uscita.
Limitazioni dovute all’attenuazione delle fibre ottiche
Le proprietà delle fibre ottiche dipendono dalla lunghezza d’onda dei modi propagativi
che viaggiano all’interno della fibra stessa, perciò la lunghezza d’onda è un parametro
di dimensionamento molto importante per un sistema di trasmissione ottico.
Si consideri un trasmettitore ottico in grado di trasmettere in fibra una potenza
media 𝑃𝑇 . Dopo 𝐿, lunghezza del mezzo trasmissivo posto lungo l’asse 𝑧, si misura una
potenza ricevuta 𝑃𝑅 < 𝑃𝑇 . Si può allora introdurre un parametro α di significato
generale, che quantifica le perdite di potenza in fibra ottica, tale che:
𝑑𝑃
= −αP
𝑑𝑧
Considerando una sistema guidante lungo 𝐿, si ottiene:
𝑃𝑅 = 𝑃𝑇 exp(−αL)
Si può esprimere il coefficiente di attenuazione in 𝑑𝑏/𝑘𝑚 :
α(dB/km) = −
10
𝑃𝑅
log10 ( )
L
𝑃𝑇
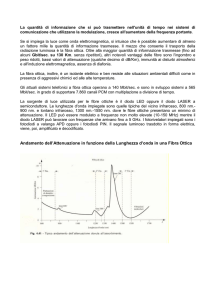
Come si osserva dalla figura seguente, l’attenuazione in fibra dipende dalla lunghezza
d’onda e presenta dei minimi locali che identificano le finestre di trasmissione
21
caratteristiche di un sistema di trasmissione ottico. I tre minimi locali in
corrispondenza di 0,8 µ𝑚, 1,33 µ𝑚 e 1,55 µ𝑚 individuano la prima, seconda e terza
finestra.
Al diminuire di 𝜆 , le perdite aumentano molto, perciò non si utilizzano modi
propagativi di lunghezza d’onda inferiore a 0,8 µ𝑚.
FIGURA 13
La prima finestra di attenuazione è stata quella usata per prima; l’energia dei fotoni
corrispondenti a 𝜆 = 0,8 µ𝑚 è sufficiente a ionizzare atomi di silicio, quindi rendono
possibile il funzionamento di fotodiodi led al silicio. Per lunghezze d’onda maggiori non
si possono più utilizzare dispositivi al silicio, per questo motivo si sono sviluppati
semiconduttori di tipo ternario come l’arseniuro di gallio fosfato GaAsP che permette
di creare LED nella seconda di finestra di attenuazione, a 1,33 µ𝑚 .
I fattori di perdita in fibra si possono distinguere in due gruppi: perdite per
assorbimento e perdite radiative.
Per quanto riguarda le perdite per assorbimento, a loro volta si dividono in intrinseche
e estrinseche.
Le perdite intrinseche sono causate dall’interazione dell’onda che si propaga nel mezzo
trasmissivo, con i componenti del vetro che costituiscono i materiali della fibra stessa.
22
Un esempio è lo spettro di assorbimento infrarosso della silice SiO2. Ciononostante, il
contributo di quest’ultimo è trascurabile nelle finestre di lunghezze d’onda di interesse
per un sistema di trasmissione ottico.
Invece, le perdite estrinseche sono causate da impurezze presenti nel materiale
come ioni dei metalli di transizione (ad esempio 𝐹𝑒 2+ , 𝐶𝑢2+ , 𝐶𝑟 3+ , etc.) che causano
perdite di assorbimento nell’intervallo di lunghezza d’onda comprese tra 0,6 µ𝑚 e
1,6 µ𝑚. Un fattore di perdita notevole è dovuto allo ione ossidrile 𝑂𝐻 − . Si raggiungono
fattori di perdita di 50 𝑑𝐵/𝑘𝑚 con una concentrazione di 1 𝑝𝑝𝑚 , perciò nasce la
necessità di ottenere delle fibre ultra-pure al fine di ridurre la concentrazione di
impurezze. Oggi si riescono ad ottenere fibre ottiche che presentano una
concentrazione di 𝑂𝐻 − minore di 1 𝑝𝑝𝑏 (una parte per miliardo). In Figura 13 si
osservano i caratteristici picchi di assorbimento dovuti allo ione ossidrile, in
corrispondenza di 1,24 µ𝑚 e 1,38 µ𝑚.
FIGURA 14
Come si osserva dalla figura precedente, si riesce a ridurre l’effetto delle perdite per
assorbimento rendendo possibile la trasmissione ottica in una finestra più larga delle
tre finestre di trasmissione caratteristiche di un sistema in fibra ottica. Questo rende
possibile l’utilizzo di un sistema di trasmissione di tipo Wavelength Division
Multiplexing (WDM), che verrà trattato in seguito.
23
Si parla di perdite radiative quando un segnale ottico in guida si accoppia con la
radiazione presente nel cladding. Lo scattering di Rayleigh è il fenomeno di perdita
radiativa predominante, ed è dovuto a inomogeneità di piccole dimensioni rispetto alla
lunghezza d’onda trasmessa, presenti all’interno della fibra. Queste imperfezioni si
formano in fase di fabbricazione e risultano in piccole fluttuazioni di densità. Ad alte
temperature le molecole di silice si orientano in modo casuale e nel momento della
realizzazione della fibra possono rimanere “congelate” causando inomogeneità nel
mezzo trasmissivo. Le perdite dovute allo scattering di Rayleigh sono proporzionali a
𝜆−4 , quindi si riducono fortemente all’aumentare della lunghezza d’onda. Più
precisamente si considera un parametro 𝛼𝑅 che quantifica le perdite dovute a questo
fenomeno, tale che:
𝛼𝑅 =
𝐶
𝜆4
con 𝐶 costante che dipende dal materiale utilizzato per la fabbricazione del core. Per
una fibra ottica in silice si ha:
𝜆0 4
𝛼(𝜆) = 𝛼0 ( )
𝜆
dove
𝛼0 = 1,7 𝑑𝐵/𝑘𝑚
e
𝜆0 = 0,85 µ𝑚
Spesso si utilizzano particolari molecole droganti come il 𝐺𝑒𝑂2, 𝑃2 𝑂5 per ottenere un
preciso indice di rifrazione. Questo porta ad un aumento delle perdite di scattering,
perciò fibre ottiche particolarmente drogate hanno solitamente alti livelli di perdite
per scattering di Rayleigh.
Si potrebbe pensare di utilizzare fibre che permettono la propagazione di modi
di lunghezza d’onda 𝜆 ≥ 2 µ𝑚, ovvero di fibre che permettono la trasmissione nello
24
spettro infrarosso. Queste avrebbero delle perdite di scattering bassissime, inoltre
particolari tipi di vetro (fluoride glasses) permetterebbero di ottenere bassi valori di
assorbimento proprio nello spettro infrarosso. Questo permetterebbe di implementare
sistemi di trasmissione in fibra ottica con un repeater spacings ≥ 1000 𝑘𝑚 .
Ciononostante, a causa di problemi di fabbricazione di questo tipo di fibre a basso
assorbimento, e a causa della difficile realizzazione di sorgenti e detectors adeguati,
questi sistemi sono ancora di difficile implementazione.
In realtà, oltre alle precedenti cause di perdita nelle fibre, ce ne sono altre dovute alle
particolari imperfezioni delle guide. Ciò che accade è che le fibre ottiche non sono mai
geometricamente perfette. Variazioni nel diametro e deformazioni locali possono
introdurre altri fattori di perdita in fibra. Si parla in questo caso di scattering di Mie, e
di solito, se il diametro della fibra non varia più del 1 %, le perdite sono inferiori a
0,03 𝑑𝐵/𝑘𝑚.
Un altro fattore di perdita è sicuramente il raggio di curvature delle fibre ottiche.
Più piccolo è il raggio di curvatura della fibra, più alte sono le perdite. In generale, a
differenza di una guida d’onda metallica, dove si ha un campo confinato da pareti
metalliche, nella guida d’onda dielettrica in fibra il campo non è confinato e si hanno
perdita di potenza per irradiazione in corrispondenza di ogni discontinuità della guida.
A causa della eccessiva curvatura, il segnale ottico tende a lasciare l’interno della fibra.
Si parla di macro-curvature se le curvature sono visibile anche dall’occhio umano, e di
micro-curvature se non lo sono. Le perdite dovute a curvature sono direttamente
proporzionali a 𝑒 −𝑅/𝑅𝑐 dove 𝑅 è il raggio di curvatura della fibra e 𝑅𝑐 = 𝑎/(𝑛12 − 𝑛22 ),
con 𝑎 raggio del core, 𝑛1 indice di rifrazione del core e 𝑛2 indice di rifrazione del
cladding. Generalmente se in una fibra monomodale si ha 𝑅 > 5 𝑚𝑚, allora questo
contributo di perdita risulta trascurabile. Una microcurvatura può causare fattori di
perdita anche di 100 𝑑𝐵/𝑘𝑚 . Oltre alle fibre, anche connettori e altri dispositivi
possono introdurre perdite nel sistema.
25
Dispersione in fibra ottica
Un altro fenomeno limitante per un sistema di trasmissione in fibra ottica è il fenomeno
della dispersione.
Applicando le equazioni di Maxwell, si ottiene che solo determinate soluzioni di queste
permettono la propagazione di onde elettromagnetiche all’interno di un sistema in
fibra ottica. È possibile considerare più modi propagativi che viaggiano
contemporaneamente nel mezzo trasmissivo. A pari distanza percorsa in fibra, i modi
si propagano con velocità diverse l’uno dall’altro. Il ritardo differenziale con cui i modi
emergono dalla fibra dà luogo al fenomeno di dispersione modale. Questo comporta un
allargamento nello spettro di trasmissione di un sistema in fibra ottica. Pur avendo un
mezzo con bassissima attenuazione, la dispersione limita fortemente la trasmissione
di segnale a velocità molto elevate.
Si può minimizzare l’effetto della dispersione modale utilizzando delle fibre
graded-index piuttosto che step-index.
FIGURA 15
Come si osserva dalla figura precedente, si utilizzano fibre con drogaggio variabile in
modo tale il raggio subisca un incurvamento meno brusco all’interfaccia core-cladding.
I raggi che seguono i percorsi più lunghi sono quelli che passano per le regioni più
estreme del nucleo, al contrario i raggi che seguono percorsi più corti sono quelli che
si mantengono molto vicino all’asse della fibra. Siccome la velocità di propagazione dei
raggi è inversamente proporzionale alla radice quadrata dell’indice di rifrazione in
guida, grazie al profilo caratteristico di una fibra graded-index (immagine a destra in
26
Figura 15) i raggi che percorrono più strada viaggiano a velocità più alta rispetto ai
raggi che viaggiano a velocità mediamente più basse.
Una possibile soluzione è quella di considerare una fibra monomodale, in modo
da eliminare completamente gli effetti della dispersione cromatica. Per fare questo
bisogna ridurre il diametro del nucleo fino a meno di 10 µ𝑚. Un problema che nasce
in questo particolare tipo di fibre è legato all’efficienza di iniezione, ovvero al fatto che
una quota parte della radiazione incidente verrà persa nel mantello. Un altro problema
è legato alle giunture tra più fibre, in quanto è necessario allineare i nuclei delle fibre
stesse.
Un altro fenomeno dispersivo caratteristico di un sistema in fibra ottica, è la dispersione
cromatica, dovuta al fatto che l’indice di rifrazione della radiazione in fibra varia con la
lunghezza d’onda. Questo fa sì che le componenti in frequenza di un determinato
segnale trasmesso si ricompongano in uscita dando luogo ad un segnale ricevuto
diverso dal segnale trasmesso.
FIGURA 16
27
Si consideri un sistema di riferimento cartesiano formato da una terna di assi destrorsa
(𝑥, 𝑦, 𝑧) , due onde piane di ampiezza 𝐸0 che viaggiano entrambe in direzione di
propagazione 𝑧, tali che:
𝐸1 (𝑥, 𝑦, 𝑧, 𝑡) = 𝐸𝑜 cos[(𝜔 − ∆𝜔)𝑡 − (𝑘 − ∆𝑘)𝑧]
𝐸2 (𝑥, 𝑦, 𝑧, 𝑡) = 𝐸𝑜 cos[(𝜔 + ∆𝜔)𝑡 − (𝑘 + ∆𝑘)𝑧]
L’onda risultante dalla somma delle due onde piane è:
𝐸𝑇𝑂𝑇 = 2𝐸0 cos(𝜔𝑡 − 𝑘𝑧) cos(∆𝜔𝑡 − ∆𝑘𝑧)
In caso di interferenza costruttiva, si avrebbe:
∆𝜔 = ∆𝑘 = 0
e quindi
𝐸𝑇𝑂𝑇 = 2𝐸0 cos(𝜔𝑡 − 𝑘𝑧)
In questo caso le due onde si sommano in fase dando luogo ad un’onda di ampiezza
doppia e velocità di fase:
𝑣𝑓 =
𝜔
𝑘
Nel caso più generico invece, il termine cos(∆𝜔𝑡 − ∆𝑘𝑧) modula l’onda che si avrebbe
nel caso di interferenza costruttiva. Si definisce velocità di gruppo, la velocità
dell’inviluppo della forma d’onda.
La velocità dell’onda risultante si ottiene differenziando la seguente relazione:
∆𝜔𝑡 − ∆𝑘𝑧 = 𝑐𝑜𝑠𝑡
𝑣𝑔 =
𝑑𝑧 ∆𝜔
=
𝑑𝑡 ∆𝑘
Il concetto di velocità di gruppo nasce dal fatto che la velocità con cui si propaga un
segnale elettromagnetico nella realtà, è diversa dalla velocità di fase. Ciò è dovuto al
28
fatto che la velocità di fase è definita per campi periodici formati da treni d’onda di
lunghezza infinita e di durata infinita. Invece nella realtà si ha sempre a che fare con
“pacchetti d’onda”, ovvero di treni d’onda di durata e lunghezza finite, che possono
essere visti come sovrapposizione di infinite onde monocromatiche di durata infinita
aventi ampiezze e fasi opportune. Ciascuna componente monocromatica si propagherà
con una velocità di fase diversa dalle altre. La forma d’onda risultante non sarà più
un’onda puramente sinusoidale. La velocità di gruppo determina la velocità
dell’informazione trasportata dal segnale trasmesso.
Nei mezzi dispersivi la velocità di gruppo è minore della velocità di fase. Alcuni
mezzi che non sono soggetti al fenomeno classico della dispersione possono avere una
velocità di gruppo maggiore della velocità di fase. Nel vuoto le due velocità coincidono.
Si consideri un mezzo trasmissivo che risenta dell’effetto della dispersione cromatica,
in cui si propaga un’onda elettromagnetica a cui è associato un vettore d’onda di
modulo:
2𝜋
𝑛(𝜆)
𝜆
𝑘 = 𝑛𝑘0 =
Considerando il differenziale totale di 𝑘 si ottiene:
𝑑𝑘 =
2𝜋
2𝜋
2𝜋𝑓
2𝜋𝑓𝑛 𝑑𝜆
𝑑𝑛 − 2 𝑛𝑑𝜆 =
𝑑𝑛 −
𝜆
𝜆
𝑐
𝑐 𝜆
Dalla definizione di velocità di fase risulta:
𝑣𝑓 =
𝑓𝜆
𝑛
da cui:
𝑑𝑓 = −
𝑣𝑓
𝑛
𝜆2
𝑑𝑓
𝑑𝜆
=−
𝑓
𝜆
29
L’ultima relazione fa vedere come per un ‘onda elettromagnetica, le variazioni relative
in termini di frequenza sono uguali ed opposte alle variazioni relative della lunghezza
d’onda.
Sostituendo quest’ultima equazione nell’espressione del differenziale totale di 𝑘, si
ottiene:
𝑑𝑘 =
𝜔
𝑑𝜔
𝑑𝑛 +
𝑛
𝑐
𝑐
da cui:
𝑑𝜔 𝑐 𝜔 𝑑𝑛
= −
𝑑𝑘 𝑛 𝑛 𝑑𝑘
Se l’indice di rifrazione fosse indipendente dalla lunghezza d’onda operativa, si
otterrebbe:
𝑣𝑔 =
𝑑𝜔 𝑐
= = 𝑣𝑓
𝑑𝑘 𝑛
Nel caso più generico invece:
𝑣𝑔 =
𝑑𝜔 𝑐 𝜔 𝑑𝑛
= −
𝑑𝑘 𝑛 𝑛 𝑑𝑘
Dalla prima equazione sul differenziale totale di 𝑘 si ottiene:
𝑑𝑘 2𝜋 2𝜋𝑛 𝑑𝜆
=
− 2
𝑑𝑛
𝜆
𝜆 𝑑𝑛
si ha:
𝑣𝑔 =
𝑐
𝑛−𝜆
𝑑𝑛
𝑑𝜆
=
𝑐
𝑁𝐺
Dove:
𝑁𝐺 = 𝑛 − 𝜆
𝑑𝑛
𝑑𝜆
𝑁𝐺 ha il significato di un indice di rifrazione detto indice di gruppo, che racchiude il
significato della dispersione cromatica. L’indice di gruppo quantifica l’indice
equivalente visto dall’onda elettromagnetica quando passa attraverso un materiale
dispersivo. Nei materiali a dispersione normale si ha un indice di gruppo che decresce
30
all’aumentare della lunghezza d’onda. In questi casi per 𝜆 crescenti l’onda si
propagherà con una velocità sempre maggiore all’interno del mezzo dispersivo. 𝑁𝐺
racchiude in sé il rallentamento della luce dovuto alla dispersione cromatica.
Si consideri una sorgente policromatica caratterizzata da una larghezza
spettrale ∆𝜆 , supponiamo di inviare un impulso di luce temporale nel mezzo
trasmissivo. Ciascuna componente spettrale risentirà di un indice di gruppo diverso, e
quindi attraverserà la guida con velocità diverse in funzione della lunghezza d’onda.
Questo causa un allargamento temporale dell’impulso, tale che:
∆𝜏 ∆𝜆
=
𝑑𝜏 𝑑𝜆
dove 𝜏 è il tempo che impiega l’impulso di luce di larghezza spettrale 𝜆 per attraversare
la fibra. Considerando un mezzo trasmissivo lungo 𝐿, si ha:
𝜏 = 𝜏(𝜆) =
𝐿
𝐿
𝐿
𝑑𝑛
= 𝑁𝐺 = [𝑛 − 𝜆 ]
𝑣𝑔 𝑐
𝑐
𝑑𝜆
Sostituendo nell’equazione precedente si ottiene:
𝐿 2 𝑑 2 𝑛 ∆𝜆
∆𝜏 = − (𝜆
)
𝑐
𝑑𝜆2 𝜆
∆𝜏 rappresenta l’allargamento temporale dello spettro del segnale trasmesso
attraverso un mezzo dispersivo.
Si definisce un fattore
∆𝜏
1 2 𝑑2𝑛
𝐷=
= − (𝜆
)
𝐿∆𝜆
𝜆𝑐
𝑑𝜆2
che quantifica l’effetto della dispersione cromatica, anche detta Group Velocity
Dispersion (GVD). 𝐷 si misura in 𝑝𝑠/(𝑘𝑚 ∙ 𝑛𝑚) e indica l’aumento della durata di un
impulso caratterizzato da una larghezza spettrale ∆𝜆 che ha percorso 1 𝑘𝑚 di fibra.
31
FIGURA 17
È interessante osservare che se si considerasse un mezzo lineare come il vetro siliceo,
poiché le componenti del segnale si propagano nel mezzo con velocità di gruppo
diverse, all’uscita della fibra esse si ricombineranno con ritardi diversi dando luogo ad
una distorsione lineare di fase.
Si osserva dalla figura precedente che in corrispondenza di 𝜆 ≈ 1,3 µ𝑚 il
coefficiente di dispersione 𝐷 è circa nullo. In realtà anche un segnale che ha uno spettro
centrato alla lunghezza d’onda della portante 𝜆0 = 𝜆𝑍𝐷 = 1,3 µ𝑚 , è soggetto a
dispersione cromatica. Infatti, siccome lo spettro del segnale ha un’estensione non
nulla intorno a 𝜆0 , sarà presente anche in questo caso un piccolo grado di dispersione.
Il coefficiente di dispersione può essere scomposto in due termini:
𝐷 = 𝐷𝑀 + 𝐷𝑊
𝐷𝑀 dipende dall’indice di rifrazione del core della fibra, mentre 𝐷𝑊 dipende dalla
geometria della fibra e da entrambi gli indici di rifrazione del core e del cladding.
Variando la geometria della fibra, è possibile spostare 𝜆𝑍𝐷 da 1,33 µ𝑚 a 1,55 µ𝑚
riducendo il fattore 𝐷𝑊 . Queste fibre sono dette fibre a dispersione traslata.
In Figura 17 è possibile individuare due regioni a seconda che 𝐷 sia positivo o negativo.
Si definiscono mezzi a dispersione normale, quei mezzi che hanno un coefficiente di
dispersione 𝐷 < 0; in questo caso al crescere di 𝜆 la velocità di propagazione dell’onda
32
aumenta. Al contrario, i mezzi caratterizzati da 𝐷 > 0, sono detti mezzi a dispersione
anomala e al crescere di 𝜆 la velocità di propagazione dell’onda diminuisce.
Per ridurre gli effetti della dispersione cromatica è possibile ridurre il diametro
del core della fibra e drogando la fibra con diossido di germanio o diossido di silicio in
modo da spostare verso destra la curva di dispersione di materia e in modo da ridurre
il diametro del core. Si potrebbe realizzare così una fibra che presenti bassi valori di
dispersione cromatica in corrispondenza sia di 𝜆 = 1300 𝑛𝑚, che di 1550 𝑛𝑚 ( fibre
dispersion flattened). Una fibra di questo tipo ha come svantaggi: l’elevato costo di
fabbricazione, l’aumento dell’attenuazione causato dal drogaggio e la difficoltà nella
giunzione tra più fibre causata dalla riduzione del core.
Un altro termine dispersivo importante in un sistema in fibra ottica, è la dispersione di
polarizzazione (PMD) che introduce un allargamento dell’impulso temporale di luce
trasmesso. L’utilizzo di una fibra di tipo monomodale permette di trascurare l’effetto
della dispersione modale, questo però non vieta la propagazione di due modi tra loro
ortogonali, polarizzati linearmente. Questi modi, per una fibra a sezione circolare, sono
degeneri, quindi hanno velocità di gruppo uguali fra loro. A causa di variazioni nel
diametro del core della fibra e nella forma stessa della guida d’onda, c’è il rischio di
perdere questa simmetria causando un differente valore nell’indice di rifrazione “visto”
da ciascun modo, e quindi una differente velocità di propagazione tra i modi. Questo
fenomeno rende la fibra un mezzo birifrangente. Si definisce un ritardo di gruppo
differenziale (DGD) che quantifica gli effetti della dispersione di polarizzazione. La
polarizzazione del campo elettrico associato ai due modi eccitati da un impulso di luce
temporale, cambia durante la propagazione in fibra ottica. A differenza della
dispersione cromatica, in questo caso il ritardo di propagazione non aumenta
linearmente con la distanza percorsa nel mezzo, e si può dimensionare come una
variabile aleatoria.
L’allargamento dell’impulso causato dalla dispersione di polarizzazione è dato da:
∆𝑇 = |
𝐿
𝐿
−
| = 𝐿|𝛽1𝑥 − 𝛽1𝑥 | = 𝐿(∆𝛽)
𝑣𝑔𝑥 𝑣𝑔𝑦
33
Capitolo 3
Sistemi Wavelength Division Multiplexing
Dalla teoria sui sistemi di trasmissione ottici, risulta che un sistema di comunicazione
in fibra può sostenere una frequenza di cifra di oltre 10 𝑇𝑏/𝑠. In realtà questo non
succede, poiché un tale sistema è limitato dagli effetti di dispersione, da effetti non
lineari di perdita, e inoltre è soggetto alle limitazioni introdotte dagli elementi
elettronici comunque presenti. Una possibile soluzione per sfruttare al meglio la
capacità di un sistema in fibra, è quella di utilizzare un sistema multicanale. Si
realizzano sistemi di multiplazione in fibra nel dominio del tempo e nel dominio della
frequenza, per mezzo di Optical Time Division Multiplexing (OTDM) e di Wavelength
Division Multiplexing (WDM).
Un sistema di tipo WDM utilizza più di una portante ottica, modulata da un segnale
elettrico che trasporta informazione. Tutte le portanti modulate vengono poi
trasmesse sulla stessa fibra ottica. In ricezione il segnale ottico viene separato nei
diversi canali, ciascuno dei quali può essere demodulato utilizzando un ricevitore
ottico.
Grazie al WDM si riesce a sfruttare al meglio la banda di un sistema di trasmissione in
fibra ottica. L’idea alla base di tale sistema, è quella di trasmettere più canali separati
da una certa distanza spettrale, nelle finestre di trasmissione corrispondenti ad un
minimo di attenuazione in fibra. Ad esempio, riducendo il picco di assorbimento
causato dalla presenza di ioni ossidrili 𝑂𝐻 − intrappolati nel reticolo vetroso si riescono
ad ottenere capacità di oltre 30 𝑇𝑏/𝑠. Un semplice sistema WDM, ad esempio, è formato
da due portanti ottiche rispettivamente di lunghezza d’onda 1550 𝑛𝑚 e 1300 𝑛𝑚.
Esistono due modi per modulare una sorgente ottica. Si parla di modulazione
diretta se il segnale modulante è la corrente di iniezione del laser, di modulazione
indiretta se la portante generata dalla sorgente laser viene modulata direttamente da
un modulatore esterno. La modulazione diretta pone un limite massimo di 10 𝐺𝑏𝑖𝑡/𝑠
sul bit rate di trasmissione, poiché una variazione nella corrente di modulazione del
laser causa una variazione nella frequenza del segnale in uscita dalla sorgente ottica, e
quindi causa un allargamento nello spettro del segnale. In caso di modulazione
34
indiretta invece, si modula il segnale generato dalla sorgente ottica per mezzo di un
modulatore esterno. A differenza del caso precedente, ora la sorgente lavora a corrente
costante, dando luogo ad una potenza di uscita stabile e ad una riga spettrale più
stretta. La modulazione indiretta permette quindi l’utilizzo di bit rate molto più alti in
trasmissione fino a 40 𝐺𝑏𝑖𝑡/𝑠 . Ciononostante, a causa dei fenomeni di dispersione,
anche in caso di modulazione esterna si utilizzano bit rate di 10 𝐺𝑏𝑖𝑡/𝑠.
Sfruttando quest’ultimo tipo di modulazione, è possibile implementare un sistema
WDM, in modo da rendere la capacità del sistema circa pari ad 𝑁 -volte quella del
singolo canale, a pari bit rate di modulazione. Grazie alla modulazione indiretta si
riescono ad ottenere distanze spettrali minori tra i canali multiplati, rispetto al caso di
modulazione diretta.
Nonostante i grossi vantaggi di un sistema WDM, solo recentemente hanno
preso luogo sistemi di questo genere, a causa dell’elevato costo dovuto all’utilizzo di
ripetitori optoelettronici nel caso di trasmissioni a grande distanza. Ad ogni stazione di
ripetizione c’è bisogno di demultiplare il segnale ricevuto nei diversi canali, e far
seguire a ciascuna sequenza di bit un altro trasmettitore ottico in ingresso allo stadio
di multiplazione. Oggi si utilizzano amplificatori Erbium Doped Fiber Amplifier (EDFA),
che permettono di amplificare contemporaneamente più lunghezze d’onda di segnale,
evitando la demultiplazione del segnale ricevuto ad ogni stazione di ripetizione. Questo
rende possibile l’implementazione di un sistema WDM per sistemi che richiedono
grandi capacità di trasmissione di dati.
FIGURA 18
La figura precedente rappresenta un esempio di sistema WDM. A ciascuna sorgente
laser è associato un segnale ottico portante che può essere modulato fino a 10 𝐺𝑏𝑖𝑡/𝑠.
La minima distanza spettrale tra i canali è limitata dall’ interchannel crosstalk, ovvero
35
quel fenomeno di interferenza elettromagnetica che nasce nelle trasmissioni di più
canali multiplati a causa del non perfetto isolamento tra i canali stessi. Quello che si
vorrebbe ottenere da un sistema del genere, è un channel spacing più piccolo possibile,
in modo da permettere la trasmissione di più canali simultaneamente. Si definisce un
parametro caratteristico di un sistema WDM, detto spectral efficiency:
𝜂𝑆 =
𝐵
∆𝜈𝑐ℎ
con 𝐵 bit rate e ∆𝜈𝑐ℎ distanza spettrale tra i segnali portanti, dove entrambi si sono
considerati uguali per tutti i canali. 𝜂𝑆 quantifica le prestazioni di un tale sistema di
comunicazione.
Le frequenze dei canali di un sistema WDM sono state standardizzate
dall’International Telecomunication Union (ITU) considerando una distanza spettrale
di 100 𝐺𝐻𝑧 tra i canali, nel range di frequenze comprese tra 186 𝑇𝐻𝑧 e 196 𝑇𝐻𝑧. Oggi
si utilizzano distanze spettrali anche di 50 𝐺𝐻𝑧, con bit rate di 40 𝐺𝑏𝑖𝑡/𝑠.
A seconda della distanza tra le lunghezze d’onda dei segnali portanti, si distinguono
sistemi Dense WDM e Coarse WDM.
In un sistema DWDM le distanze spettrali tra le frequenze dei segnali portanti sono
molto basse, in modo da riuscire ad ottenere il maggior numero di portanti possibile in
un ristretto intervallo di lunghezze d’onda. Questo tipo di sistema rende possibile la
trasmissione di 40 canali nella terza finestra di trasmissione, centrata a 1550 𝑛𝑚 .
Riducendo la distanza tra le righe spettrali, si riesce a trasmettere fino a 160 canali
contemporaneamente su una stessa fibra ottica. Ovviamente una tale densità di canali
richiede dispositivi come filtri, multiplexer, add-drop multiplexer etc. in grado di
separare al meglio le diverse lunghezze d’onda; inoltre c’è bisogno di un sistema di
controllo in temperatura, dato che la lunghezza d’onda del segnale emesso da una
sorgente laser varia di circa 0,08 𝑛𝑚 per grado centigrado. La selettività in frequenza
dei componenti ottici che vengono utilizzati comporta un aumento del costo di un
sistema DWDM, a causa della maggior difficoltà nei processi di fabbricazione di tali
dispositivi.
36
Non sempre è richiesto un sistema di trasmissione per tratte a lunga distanza. In questo
caso, un sistema DWDM potrebbe essere troppo costoso e non necessario. Ad esempio
nel caso di Metropolitan Area Networks non sono richieste tali prestazioni, non
necessitano di tratte di amplificazione del segnale multiplato, è quindi possibile
implementare un sistema di tipo CWDM. L’idea alla base di un tale sistema, è quella di
rendere la frequenza del segnale portante indipendente dalla frequenza delle portanti
dei canali adiacenti. In questo caso non sono necessari sistemi di controllo della
temperatura della sorgente laser, e neanche dispositivi ottici passivi a banda molto
selettiva intorno alla frequenza centrale di canale. La distanza in termini di lunghezza
d’onda tra i canali è di 20 𝑛𝑚, nel range tra 1290 𝑛𝑚 e 1610 𝑛𝑚. Si osservi che tale
range comprende il picco di assorbimento dovuto allo ione 𝑂𝐻 − . Perciò in tali
applicazioni, è preferibile utilizzare fibre a basso contenuto di ioni ossidrili.
Analisi e caratterizzazione di alcuni componenti di un sistema
DWDM
In seguito verranno riportati alcuni cenni teorici sui dispositivi principali di un sistema
DWDM, insieme alle caratterizzazioni effettuate per un sistema di distribuzione di
clock per l’esperimento TOTEM all’LHC del CERN.
Sorgente laser
I segnali portanti in un sistema di tipo DWDM, sono generati da un particolare tipo di
diodo laser: il Distributed Feedback laser (DFB).
Un diodo laser non è altro che un semiconduttore a giunzione p-n alimentato da una
corrente, in cui è possibile sostenere un meccanismo di emissione stimolata sopra una
certa condizione di soglia.
Affinché il diodo funzioni da laser, c’è bisogno della contemporanea presenza di un
meccanismo di retroazione ottica e di inversione di popolazione. Per ottenere
quest’ultima condizione, in una certa regione della giunzione, devono essere presenti
37
contemporaneamente elettroni in stato eccitato e lacune. Questo si ha nelle giunzioni
fortemente drogate.
FIGURA 19
Come si osserva dalle figure precedenti, in una giunzione fortemente drogata, con
elevate concentrazioni di drogaggio di tipo 𝑛+ e 𝑝+ , il livello di Fermi cade sia in banda
di conduzione, che in banda di valenza. Considerando 𝑝+ < 𝑛+ , si può supporre che il
fenomeno dell’emissione stimolata sia prevalentemente dovuto agli elettroni.
Condizionati dal campo elettrico esterno, si possono concentrare più elettroni in banda
di conduzione di quelli che ci sarebbero all’equilibrio termodinamico. In questo modo
si ottiene il fenomeno di inversione di popolazione, e quindi si ottiene un aumento della
probabilità che avvengano ricombinazioni radiative. I fotoni prodotti possono essere
assorbiti dagli elettroni in banda di valenza, oppure possono stimolare gli elettroni in
banda di conduzione per produrre fotoni coerenti per emissione stimolata. La sorgente
di un diodo laser è una sorgente elettronica, generalmente fornita da una corrente.
38
Per ottenere un laser si sottopongono a lucidatura due facce parallele del
materiale della giunzione, in modo da ottenere una cavità Fabry-Perot, che permette
l’accumulo della radiazione introducendo un meccanismo di risonanza nella struttura
del diodo. Con un laser a semiconduttore si riescono a raggiungere valori di efficienza
più elevati di un laser a gas. I diodi laser sono caratterizzati dall’avere una purezza
spettrale maggiore di quella di un diodo LED e minore di quella di un laser a livelli
discreti.
La caratteristica potenza ottica in uscita del laser in funzione della corrente di
pompaggio, dipende fortemente dalla temperatura. Infatti, un aumento della
temperatura di lavoro causa uno spostamento della caratteristica del laser verso valori
di soglia di corrente più elevati e pendenze più basse sopra soglia. Questo succede
perché all’aumentare della temperatura, il moto di agitazione termica si oppone al
flusso di elettroni che causa emissione stimolata, riducendo l’efficienza del laser.
Per avere una sorgente robusta alle variazioni di temperatura, servirebbe un
sistema di stabilizzazione in temperatura. Una variazione di quest’ultima potrebbe
portare il laser ad emettere alla frequenza di un altro modo longitudinale, rispetto a
quello desiderato.
Sostituendo gli specchi che costituiscono gli estremi della cavità Fabry-Perot,
con una corrugazione periodica di indice di rifrazione, si riescono ad ottenere sorgenti
molto selettive in termini di frequenza di emissione. Laser a semiconduttore di questo
genere sono detti laser a feedback distribuito DFB.
FIGURA 20
39
La corrugazione periodica di periodo 𝛬 , divide due regioni ad indice di rifrazione
diverso. Se il reticolo è disposto in direzione di propagazione dei fotoni, può fungere da
specchio. Più precisamente, affinché due raggi riflessi dal reticolo a distanza 𝛬 si
sommino in fase generando interferenza costruttiva, la differenza tra i cammini ottici
percorsi deve essere un multiplo intero di lunghezza d’onda. Si ottiene, considerando i
due raggi incidenti paralleli fra di loro:
2𝑛𝛬 = 𝑚𝜆
con 𝑚 = 0,1,2, … Per 𝑚 = 1, si ha la condizione di Bragg:
2𝑛𝛬 = 𝜆
Se vale la precedente relazione, allora il reticolo funge da specchio, e gli specchi
caratteristici di una cavità Fabry-Perot non risultano essere necessari in tali tipi di
sorgenti ottiche. Grazie alla condizione di Bragg, anche in presenza di più lunghezze
d’onda, la scelta del reticolo selezione la 𝜆 che sopravvive all’interno del materiale. Per
quanto riguarda le condizioni di interferenza costruttiva per 𝑚 > 1, queste comportano
un efficienza minore rispetto alla condizione di Bragg. Più il reticolo è lungo, più la radiazione
viene immagazzinata all’interno del materiale. Nel complesso il laser risulta più stabile in
termini di lunghezza d’onda di emissione, potendo selezionare il modo longitudinale di
emissione sfruttando la capacità filtrante a banda stretta di una sorgente DFB .
In un laser di questo tipo, un cambiamento nella temperatura del dispositivo, causa una
variazione nell’indice di rifrazione, dovuta ad espansione termica e alle variazioni del gap di
banda proibita con la temperatura. Il cambiamento di indice di rifrazione genera una
variazione nel periodo della corrugazione, e quindi fa cambiare la lunghezza d’onda di
emissione del laser, che porta alla definizione di un Tunable Diode Laser (TDL).
Laser a feedback distribuito sono molto utilizzati nei sistemi di comunicazione DWDM,
dove c’è bisogno di una sorgente stabile in termini di lunghezza d’onda di emissione, e tunabile
intorno alla frequenza del segnale a centro canale.
40
Potenza ottica in funzione della corrente di alimentazione di un laser DFB
Di seguito viene riportata la caratteristica misurata al variare della corrente di
pompaggio, di un laser DFB con 𝜆 = 1550 𝑛𝑚 per diversi valori di temperatura:
FIGURA 21
La Figura 21 conferma quanto detto in precedenza: un aumento della temperatura della
sorgente laser comporta un aumento della corrente di soglia e una riduzione della pendenza
della caratteristica sopra soglia, ovvero una riduzione dell’efficienza della sorgente.
41
Isolatore ottico
Un isolatore ottico non è altro che l’equivalente ottico di un diodo. Permette la
trasmissione di segnali ottici solo in una direzione e non nella direzione opposta. Un
dispositivo del genere permette di proteggere le sorgenti WDM dalle riflessioni
provenienti da altri dispositivi ottici o connettori, che possono interferire con
l’oscillazione portante del laser.
FIGURA 22
Dalla figura precedente si può dedurre facilmente il funzionamento di un tale
dispositivo. La luce proveniente dalla guida ottica passa attraverso un polarizzatore,
un rotatore di Faraday e infine un altro polarizzatore. Lo stesso vale per l’onda che si
propaga in direzione opposta.
Consideriamo prima il percorso in avanti dell’onda. Consideriamo in ingresso al
primo polarizzatore, un’onda non polarizzata. Questa può essere scomposta in due
onde polarizzate linearmente lungo due direzioni ortogonali, una delle due parallela
all’asse ottico del polarizzatore. Quest’ultimo assorbe l’onda polarizzata in direzione
ortogonale al suo asse ottico, mentre non modifica l’onda polarizzata linearmente
lungo la direzione parallela a questo, proprietà nota come dicroismo. L’onda viene fatta
passare attraverso un rotatore di Faraday che ruota la polarizzazione dell’onda in
ingresso di 45°. In uscita dal rotatore di Faraday l’onda incontra un altro polarizzatore
che ha asse ottico parallelo alla propria polarizzazione, e quindi passa inalterata.
Al contrario, consideriamo il percorso dell’onda che si propaga in verso opposto.
Si supponga ancora in ingresso al primo polarizzatore (quello a destra in Figura 22),
42
un’onda non polarizzata. In uscita da questo avremo un’onda polarizzata linearmente
in direzione parallela all’asse ottico del polarizzatore. Il rotatore di Faraday è un
dispositivo che ruota la polarizzazione dell’onda di un certo angolo, sempre nella stessa
direzione, indipendentemente dal verso di propagazione dell’onda. All’uscita di
quest’ultimo, si ottiene un’onda polarizzata linearmente in direzione ortogonale
all’asse ottico del secondo polarizzatore. Questo fa sì che l’onda che torna indietro
venga completamente assorbita dal polarizzatore di sinistra.
Caratterizzazione di un isolatore ottico
FIGURA 23
Per la caratterizzazione dell’isolatore ottico si è proceduto connettendo la sorgente
WDM ad un accoppiatore direzionale, utilizzato come strumento di misura. Dalla
potenza ottica misurata dal power meter sul ramo di monitor dell’accoppiatore si è
ricavata la potenza ottica in ingresso all’isolatore sfruttando il coupling ratio
dell’accoppiatore direzionale.
Per il calcolo dell’insertion loss 𝐼𝐿 si è collegato il ramo di test dell’accoppiatore
alla porta 1 dell’isolatore ottico. Dalla potenza in uscita alla porta 2 si è ricavato il
fattore di insertion loss del dispositivo.
FIGURA 24
43
Allo stesso modo si è connessa la sorgente WDM all’accoppiatore direzionale, poi si è
collegato il ramo di test dell’accoppiatore alla porta 2 dell’isolatore. Dalla potenza in
uscita dalla porta 1 si è misurato il fattore di isolation 𝐼 del dispositivo.
Per la misura del return loss 𝑅𝐿 del dispositivo, dalla prima configurazione, si è
misurata la potenza in uscita dal ramo isolato dell’accoppiatore (𝑃6 in Figura 24), e
tramite il fattore di accoppiamennto di quest’ultimo si è calcolata la potenza di
backreflection del dispositivo.
Di seguito vengono riportati i valori dei parametri dell’isolatore, caratterizzato alla
lunghezza d’onda centrale dei canali 𝐼𝑇𝑈 32, 𝐼𝑇𝑈 34, 𝐼𝑇𝑈 36:
Parametro
𝐼𝐿
𝐼
𝑅𝐿
Misura
𝑃2
𝑃1
𝑃4
−10𝑙𝑜𝑔10
𝑃3
𝑃5
−10𝑙𝑜𝑔10
𝑃1
−10𝑙𝑜𝑔10
ITU32
𝟏𝟓𝟓𝟏, 𝟕𝟐 𝒏𝒎
ITU34
𝟏𝟓𝟓𝟎, 𝟏𝟐 𝒏𝒎
ITU36
𝟏𝟓𝟒𝟖, 𝟕𝟏 𝒏𝒎
0,63 𝑑𝐵
0,66 𝑑𝐵
0,6 𝑑𝐵
50,51 𝑑𝐵
50,94 𝑑𝐵
48,15 𝑑𝐵
46,31 𝑑𝐵
40,48 𝑑𝐵
40,32 𝑑𝐵
TABELLA 1
44
Circolatore
FIGURA 25
Il principio di funzionamento di un circolatore è alquanto semplice. Facendo
riferimento alla Figura 25, la potenza in ingresso alla porta 1 viene trasmessa alla porta
2, la potenza in ingresso alla porta 2 viene trasmessa alla porta 3 e la potenza in
ingresso alla porta 3 non viene trasmessa né alla porta 1, né alla porta 2. La terza porta
è isolata dalle altre 2.
FIGURA 26
Consideriamo un’onda non polarizzata in ingresso al primo walk-off block, che è un
blocco di materiale birifrangente. L’onda che si propaga all’interno del materiale, si può
scomporre in due onde polarizzate linearmente lungo direzioni ortogonali fra di loro.
L’onda che non cambia direzione di propagazione all’interno del mezzo birifrangente,
rispetto all’onda incidente all’interfaccia tra aria e cristallo, è detta onda ordinaria.
Questa vede il mezzo come se fosse isotropo. Al contrario, l’altra componente, detta
onda straordinaria, viene deviata dal mezzo materiale a causa delle proprietà
45
anisotrope di quest’ultimo. In uscita dal primo wolk-off block si ottengono due onde
polarizzate linearmente che viaggiano nella stessa direzione, con polarizzazioni fra
loro ortogonali. Sia l’onda straordinaria che l’onda ordinaria passano attraverso un
rotatore di Faraday, che ruota di 45° la polarizzazione di entrambe. Subito dopo
attraversano un half-wave plate, anche questo un dispositivo ottico di materiale
birifrangente, che ruota di ulteriori 45° lo stato di polarizzazione di entrambe. L’ultimo
walk-off block ha effetto opposto al primo, e permette di ricombinare le due
componenti in uscita verso la porta 2. In tutto gli stati di polarizzazione di entrambe le
onde sono stati ruotati di 90°.
FIGURA 27
Si consideri ora il percorso di un’onda non polarizzata in ingresso alla porta 2. Questa
viene scomposta in due onde polarizzate linearmente lungo direzioni fra loro
perpendicolari dal wolk-off block di destra (Figura 27). L’half-wave plate ruota la
polarizzazione delle due onde in senso opposto rispetto al caso precedente, in quanto
non fa altro che ritardare l’onda polarizzata linearmente in direzione parallela al
proprio asse ottico rispetto all’onda polarizzata in direzione ortogonale, in modo da
ottenere uno sfasamento in uscita corrispondente a mezza lunghezza d’onda. Questo
corrisponde ad una rotazione dello stato di polarizzazione di un certo angolo, sempre
nello stesso senso di rotazione rispetto alla direzione di propagazione dell’onda. Il
rotatore di Faraday, invece, ruota di 45° la polarizzazione di entrambe in modo da farle
tornare nelle stesse condizioni di polarizzazione delle onde in ingresso all’half-wave
plate. L’ultimo walk-off block, separa ulteriormente le due onde che vengono
ricombinate insieme per mezzo di un beam splitter.
46
Caratterizzazione di un circolatore ottico
Per la caratterizzazione del circolatore ottico (Figura 25) si è proceduto connettendo
la sorgente WDM ad un accoppiatore direzionale, utilizzato come strumento di misura.
Dalla potenza ottica misurata dal power meter sul ramo di monitor dell’accoppiatore
si è ricavata la potenza ottica in ingresso al circolatore, come è stato fatto in precedenza
per l’isolatore ottico.
Si è collegato il ramo di test dell’accoppiatore alla porta 1 del circolatore ottico.
Dalla potenza in uscita alla porta 2 e alla porta 3 si sono ricavati il fattore di insertion
loss 𝐼𝐿(1 > 2) e il fattore di directivity 𝐷(1 > 3) del dispositivo. In seguito si è
collegato il ramo di test dell’accoppiatore alla porta 2 del circolatore ottico. Dalla
potenza in uscita alla porta 2 e alla porta 3 si sono ricavati i fattori di isolation 𝐼(2 > 1)
e il fattore di insertion loss 𝐼𝐿(2 > 3) del dispositivo. Allo stesso modo si è collegato il
ramo di test dell’accoppiatore alla porta 3 del circolatore ottico. Dalla potenza in uscita
alla porta 1 e alla porta 2 si sono ricavati i fattori di directivity 𝐷(3 > 1) e il fattore di
isolation 𝐼(3 > 2) del dispositivo.
FIGURA 28
Per la misura del return loss 𝑅𝐿(1), 𝑅𝐿(2), 𝑅𝐿(3) del dispositivo sulle tre porte, si è
proceduto come nella caratterizzazione dell’isolatore ottico considerando come
ingresso al ramo di test dell’accoppiatore rispettivamente la prima, la seconda e la terza
porta del circolatore.
47
Di seguito vengono riportati i valori dei parametri del circolatore, caratterizzato alla
lunghezza d’onda centrale dei canali 𝐼𝑇𝑈 32, 𝐼𝑇𝑈 34, 𝐼𝑇𝑈 36:
Parametro
𝐼𝐿(1 > 2)
𝐼𝐿(2 > 3)
𝐼(2 > 1)
𝐼(3 > 2)
𝐷(1 > 3)
𝐷(3 > 1)
𝑅𝐿(1)
𝑅𝐿(2)
𝑅𝐿(3)
Misura
𝑃1>2
𝑃1
𝑃2>3
−10𝑙𝑜𝑔10
𝑃2
𝑃2>1
−10𝑙𝑜𝑔10
𝑃2
𝑃3>2
−10𝑙𝑜𝑔10
𝑃3
𝑃1>3
−10𝑙𝑜𝑔10
𝑃1
𝑃3>1
−10𝑙𝑜𝑔10
𝑃3
𝑃1>1
−10𝑙𝑜𝑔10
𝑃1
𝑃2>2
−10𝑙𝑜𝑔10
𝑃2
𝑃3>3
−10𝑙𝑜𝑔10
𝑃3
−10𝑙𝑜𝑔10
ITU32
𝟏𝟓𝟓𝟏, 𝟕𝟐 𝒏𝒎
ITU34
𝟏𝟓𝟓𝟎, 𝟏𝟐 𝒏𝒎
ITU36
𝟏𝟓𝟒𝟖, 𝟕𝟏 𝒏𝒎
0,71 𝑑𝐵
0,76 𝑑𝐵
0,77 𝑑𝐵
1,05 𝑑𝐵
0,95 𝑑𝐵
1,14 𝑑𝐵
58,08 𝑑𝐵
≥ 59,44 𝑑𝐵
≥ 59,59 𝑑𝐵
54,23 𝑑𝐵
58,71 𝑑𝐵
54,49 𝑑𝐵
55,23 𝑑𝐵
54,44 𝑑𝐵
58,59 𝑑𝐵
≥ 59,23 𝑑𝐵
≥ 59,44 𝑑𝐵
≥ 59,59 𝑑𝐵
41,44 𝑑𝐵
≥ 55,61 𝑑𝐵
53,91 𝑑𝐵
≥ 55,4 𝑑𝐵
≥ 55,61 𝑑𝐵
54,66 𝑑𝐵
53,44 𝑑𝐵
≥ 55,61 𝑑𝐵
≥ 55,91 𝑑𝐵
48
Multiplexer a Demultiplexer
Multiplexer e demultiplexer sono elementi fondamentali in un sistema di trasmissione
WDM. A seconda della struttura di tali elementi, i demultiplexer si possono suddividere
in due grandi categorie: i Diffraction-based demultiplexer e gli interference-based
deumultiplexer. In entrambe le tipologie, uno stesso dispositivo può essere utilizzato
da multiplexer o da demultiplexer, a seconda della direzione di propagazione dell’onda
incidente, per principio di invertibilità del cammino ottico.
I diffraction-based demultiplexer sfruttano il fenomeno di diffrazione della luce
da un reticolo di Bragg.
FIGURA 29
Il segnale di ingresso multiplato viene focalizzato da una lente verso il reticolo, posto
nel fuoco della lente stessa. Il compito del reticolo di diffrazione è quello di separare le
diverse lunghezze d’onda del segnale multiplato, e focalizzare ciascuna portante in una
fibra ottica. Per ottenere un dispositivo facilmente integrabile, conviene utilizzare delle
lenti a gradiente di indice (Graded-index lens, GRIN), ovvero un particolare tipo di lenti
fabbricate in modo da ottenere una variazione graduale dell’indice di rifrazione del
materiale. Sostanzialmente la luce viene continuamente incurvata dal materiale finché
49
non viene focalizzata in un punto, come una lente convenzionale. Grazie alla condizione
di Bragg è possibile ottenere un fenomeno di interferenza costruttiva tale che:
𝜆0 = 2𝑛𝑒𝑓𝑓 𝛬
con 𝑛𝑒𝑓𝑓 indice di rifrazione effettivo del modo guidato in fibra. Il reticolo rifletterà
maggiormente la portante di lunghezza d’onda 𝜆0 , che verrà focalizzata nella fibra in
uscita. È ovvio che per ottenere un demultiplexer c’è bisogno di creare più reticoli di
Bragg all’interno del materiale, perché ciascun reticolo da solo è in grado di riflettere
una sola lunghezza d’onda. Data l’elevata complessità nella fabbricazione di un tale
dispositivo, si preferisce utilizzare dei reticoli di Bragg concavi inseriti direttamente
nella fibra. Questi ultimi dispositivi permettono di multiplare e demultiplare fino a 120
canali contemporaneamente.
Per quanto riguarda gli Interference-based demultiplexer, questi sfruttano
dispositivi come filtri ottici e accoppiatori direzionali, selezionando la lunghezza
d’onda riflessa mediante il fenomeno dell’interferenza ottica. L’analisi di questi ultimi
esula dai fini di questa tesi.
Caratterizzazione di un mutliplexer ottico
Per la caratterizzazione del multiplexer ottico si è proceduto connettendo la sorgente
WDM ad un accoppiatore direzionale, utilizzato come strumento di misura. Anche in
questo caso, dalla potenza ottica misurata dal power meter sul ramo di monitor
dell’accoppiatore si è ricavata la potenza ottica in ingresso al multiplexer mediante il
coupling ratio dell’accoppiatore.
Si è collegato il ramo di test dell’accoppiatore alla porta 𝐶𝐻32 del multiplexer. È
stato valutato il coefficiente di trasmissione in potenza del multiplexer misurando la
potenza in uscita dalla porta comune e variando la lunghezza d’onda del segnale
generato dal laser di ∆𝜆 = 0,1 𝑛𝑚 in un intervallo prefissato di lunghezze d’onda:
50
FIGURA 30
Si è ripetuto lo stesso procedimento connettendo il ramo di test dell’accoppiatore alla
porta 𝐶𝐻34 del multiplexer:
FIGURA 31
Di seguito vengono riportati i grafici di trasmissione del multiplexer:
FIGURA 32
Come si osserva dalla figura precedente, considerando la porta 𝐶𝐻32 del multiplexer,
si ottiene un massimo di trasmissione in corrispondenza della lunghezza d’onda
51
centrale del canale 𝐼𝑇𝑈32. Per quanto riguarda la porta 𝐶𝐻34, si ottiene un massimo
di trasmissione in corrispondenza della lunghezza d’onda centrale del canale 𝐼𝑇𝑈34.
Add-drop multiplexer
FIGURA 33
Un optical add-drop multiplexer (OADM), è un dispositivo ottico che permette di
aggiungere o rimuovere uno o più canali di un sistema multiplato senza interferire con
i canali restanti. Tale dispositivo utilizza contemporaneamente un multiplexer, un
demultiplexer e uno o più switch ottici. Il segnale multiplato in ingresso al
demultiplexer viene separato nei diversi canali. Uno o più switch ottici sono utilizzati
per rimuovere, aggiungere o lasciar passare inalterati i canali demultiplati in ingresso
al multiplexer, che ha il compito di ricombinarli insieme in un unico segnale multiplato.
Il grosso vantaggio offerto da un OADM è la possibilità di amplificare ed equalizzare un
singolo canale di un sistema WDM, grazie alla possibilità di controllare singolarmente
ciascuno di essi.
Se non è necessario controllare singolarmente tutti i canali di un segnale
multiplato, ma si ha la necessità di demultiplare un singolo canale, si possono utilizzare
52
sistemi meno complessi che utilizzano add-drop filters in grado di estrarre un singolo
canale senza alterare il segnale del sistema WDM.
Caratterizzazione di un add-drop multiplexer
Per l’analisi delle caratteristiche dell’ add-drop, si è connessa la sorgente WDM ad un
accoppiatore direzionale, utilizzato come strumento di misura. Dalla potenza ottica
misurata dal power meter sul ramo di monitor dell’accoppiatore si è ricavata la potenza
ottica in ingresso al OADM.
Si è collegato il ramo di test dell’accoppiatore alla porta di ingresso dell’add-drop. È
stato valutato il coefficiente di trasmissione in potenza dalla porta di ingresso alla porta
d’uscita misurando potenza della porta di uscita e variando la lunghezza d’onda del
segnale generato dal laser ogni ∆𝜆 = 0,1 𝑛𝑚 in un intervallo prefissato di lunghezze
d’onda:
FIGURA 34
Si è poi misurato il coefficiente di trasmissione in potenza dalla porta di uscita alla
porta di 𝐴𝐷𝐷 allo stesso modo del caso precedente, mandando segnale alla porta di
uscita e misurando potenza alla porta di 𝐴𝐷𝐷:
FIGURA 35
53
Di seguito vengono riportati i grafici di trasmissione dell’add-drop multiplexer:
FIGURA 36
Come si osserva dalla figura precedente, in corrispondenza della lunghezza d’onda
centrale del canale 𝐼𝑇𝑈36 si ha un minimo di trasmissione dalla porta di ingresso alla
porta di uscita. Inoltre, per lo stesso valore di lunghezza d’onda, si ha un massimo di
trasmissione dalla porta di uscita alla porta di 𝐴𝐷𝐷 . Infatti, essendo l’add-drop
multiplexer un dispositivo reciproco, la porta di 𝐴𝐷𝐷 si comporta da 𝐷𝑅𝑂𝑃 se il
segnale di ingresso è posto sulla porta di uscita.
54
Fiber Bragg Gratings
FIGURA 37
Un reticolo di Bragg in fibra è una variazione periodica dell’indice di rifrazione del
materiale di cui è composto il core. Questa si forma grazie all’utilizzo di radiazioni
ultraviolette in grado di “scrivere” il reticolo all’interno di fibre fortemente drogate con
particelle di alluminio. Grazie alla struttura periodica, le onde riflesse che incidono a
distanza di una lunghezza d’onda di reticolo 𝛬 sul FBG, interferiscono
costruttivamente. La lunghezza d’onda corrispondente è detta lunghezza d’onda di
Bragg:
𝜆𝐵 = 2𝑛𝛬
con 𝑛 indice di rifrazione del core della fibra ottica. In Figura 37 si può osservare la
potenza incidente sul reticolo, la potenza riflessa dal reticolo e la potenza trasmessa
dal reticolo in funzione della lunghezza d’onda del segnale che viaggia nella guida
d’onda.
Il periodo del reticolo varia con la temperatura. Ovviamente questo comporta
una variazione della lunghezza d’onda riflessa dal reticolo stesso. Questa caratteristica
rende possibile l’utilizzo di tali dispositivi come sensori di temperatura.
È inoltre possibile utilizzare contemporaneamente un circolatore e un FBG,
come add-drop multiplexer. Il segnale multiplato va in ingresso alla porta 1 del
circolatore, in uscita dalla porta 2 viene posto il reticolo di Bragg in fibra che lascia
55
passare inalterate le componenti spettrali del segnale multiplato, tranne quella
corrispondente alla lunghezza d’onda di Bragg. Quest’ultima viene demultiplata dal
reticolo che la riflette verso la porta 3.
Caratterizzazione di un FBG
Per la caratterizzazione del reticolo di Bragg in fibra, si è connessa la sorgente WDM ad
un accoppiatore direzionale, utilizzato come strumento di misura. Il ramo di test
dell’accoppiatore direzionale è stato collegato in ingresso alla porta 1 del circolatore.
La porta 2 di quest’ultimo è stata collegata all’FBG, in modo da permettere la misura
del coefficiente di trasmissione e di riflessione del dispositivo, e in modo da limitare le
backreflections verso la sorgente DFB:
FIGURA 38
È stato valutato il coefficiente di trasmissione in potenza del reticolo in funzione della
lunghezza d’onda della sorgente laser, misurando la potenza ottica in uscita dall’FBG
ogni ∆𝜆 = 0,02 𝑛𝑚 in un intervallo prefissato di lunghezze d’onda e considerando il
fattore di insertion loss 𝐼𝐿(1 > 2) introdotto dal circolatore. In seguito si è valutato il
coefficiente di riflessione in potenza del reticolo valutando la potenza in uscita dalla
porta 3 del circolatore, sempre tenendo in conto delle perdite introdotte dal
circolatore, 𝐼𝐿(2 > 3).
Di seguito vengono riportati i grafici corrispondenti al coefficiente di trasmissione e di
riflessione in potenza:
56
FIGURA 39
In corrispondenza della lunghezza d’onda centrale del canale di trasmissione 𝐼𝑇𝑈36, si
ottiene un minimo valore del coefficiente di trasmissione e un massimo valore del
coefficiente di riflessione in potenza. Si osserva inoltre che per lunghezze d’onda
corrispondenti ai canali adiacenti 𝜆𝐶𝐻35 = 1549,32 𝑛𝑚 e 𝜆𝐶𝐻37 = 1547,72 𝑛𝑚 il
reticolo lascia passare la radiazione senza causare eccessive riflessioni, avendo un
coefficiente di trasmissione in potenza maggiore di −0,7 𝑑𝐵 e un coefficiente di
riflessione minore di −20 𝑑𝐵.
Capitolo 4
Mach Zehnder modulator
Per ottenere sistemi di comunicazione di tipo DWDM, si sono rese necessarie nuove
tecniche di modulazione delle portanti ottiche, al fine di garantire una maggior purezza
spettrale e una minor distanza in frequenza tra i canali di un sistema multiplato. Questo
comporta l’utilizzo di tecniche di modulazione che non influenzino la sorgente, che non
causino shift nella frequenza del segnale ottico. Il Mach Zehnder modulator è un
modulatore ottico che permette di utilizzare tecniche di modulazione indiretta della
sorgente laser in modo da ottenere tali prestazioni.
57
FIGURA 40
Il modulatore è formato da una guida d’onda seguita da una serie di due accoppiatori.
La potenza trasmessa dalla radiazione in guida, viene divisa in parti uguali nei due rami
del modulatore. In uscita il secondo accoppiatore ricombina i segnali dopo che hanno
percorso lo stesso cammino geometrico.
Grazie agli elettrodi disposti lungo uno dei due rami, è possibile creare una
modulazione di fase nel segnale ottico che attraversa il braccio su cui sono applicati.
Più precisamente, applicando una tensione agli elettrodi, si genera uno sfasamento
direttamente proporzionale alla tensione applicata. Questo è dovuto all’effetto
elettroottico di particolari materiali birifrangenti come il niobato di lito 𝐿𝑖𝑁𝑏𝑂3 , per il
quale si ha una variazione in forma e dimensioni dell’indicatrice ottica del mezzo in
funzione del campo elettrico applicato al materiale stesso. L’effetto Pockels rappresenta
la componente lineare dell’effetto elettroottico, l’effetto Kerr è la componente
direttamente proporzionale al quadrato del campo elettrico applicato, spesso
trascurabile rispetto all’effetto lineare.
Considerando una tensione nulla ai capi degli elettrodi, il segnale viene diviso in due
onde che non subiscono variazioni di fase nel passaggio attraverso il modulatore. In
uscita si ottiene la somma di due segnali in fase fra di loro, e quindi si ha esattamente
il segnale in ingresso al modulatore. Se invece si applica una tensione 𝑉 ≠ 0 ai capi
degli elettrodi, tale da ottenere uno sfasamento di 𝜋 del segnale che passa attraverso il
ramo superiore (Figura 40), si osserva un fenomeno di interferenza distruttiva tra i
segnali in uscita dai due rami; tale valore di tensione è detto tensione di semionda 𝑉𝜋 .
Per valori di tensione 𝑉, tali che 0 < 𝑉 < 𝑉𝜋 si ottiene una modulazione di ampiezza del
segnale portante.
58
FIGURA 41
Dalla figura precedente si osserva come l’uscita del dispositivo presenta una
dipendenza sinusoidale dal campo applicato agli elettrodi, quindi, se il dispositivo
viene polarizzato esattamente nel punto di massimo guadagno, considerando un
piccolo segnale in ingresso al modulatore, si ottiene, in prima approssimazione, una
variazione lineare dell’irradianza in uscita in funzione di 𝑉𝑏𝑖𝑎𝑠 . I punti di massimo e di
minimo della precedente caratteristica corrispondono a punti di funzionamento non
lineare del modulatore.
59
Analisi di alcune caratteristiche del Mach Zehnder modulator
In teoria la caratteristica potenza ottica in uscita del modulatore, in funzione della
tensione applicata al Mach Zehnder dovrebbe essere una funzione cosinusoidale, in
quanto la potenza ottica del segnale in uscita è pari al modulo quadro della somma di
due segnali sinusoidali sfasati fra di loro di un angolo direttamente proporzionale alla
tensione applicata. Ovviamente tale caratteristica è fortemente non lineare. Nelle
applicazioni lineari come nel caso della modulazione d’ampiezza di portanti ottiche,
quello che si cerca di ottenere è un punto di lavoro stabile in corrispondenza del punto
di massima linearità della caratteristica, ovvero nel punto di massima derivata (Figura
41). Una variazione nella posizione del punto di lavoro di tale dispositivo, può causare
un funzionamento fortemente non lineare, con la comparsa di armoniche spurie nello
spettro del segnale in uscita. Risulta sperimentalmente che la caratteristica 𝑃𝑜𝑢𝑡 − 𝑉𝑏𝑖𝑎𝑠
si sposta nel tempo, causando variazioni nella posizione del punto operativo. Questo
può portare il dispositivo ad un funzionamento non lineare, nonostante inizialmente
sia stato polarizzato esattamente nel punto di massima linearità. Questo fenomeno è
dovuto ad alcune caratteristiche dei materiali di cui è composto il modulatore, come ad
esempio il niobato di litio 𝐿𝑖𝑁𝑏𝑂3 ; può essere causato da effetto piroelettrico, effetto
fotorifrattivo e fenomeni fotoconduttivi che avvengono contemporaneamente nel
𝐿𝑖𝑁𝑏𝑂3 . Sorge perciò la necessità di un circuito di controllo automatico del punto di
lavoro in grado di garantire sempre un funzionamento lineare del dispositivo. Alcuni
costruttori, infatti, permettono di rivelare la portante ottica con un fotodiodo installato
nel case del dispositivo. In questo modo è possibile monitorare il segnale in uscita dal
modulatore evitando l’utilizzo di un accoppiatore in uscita.
Di seguito vengono riportate alcune caratteristiche misurate su un Mach Zehnder
modulator.
60
FIGURA 42
Per la caratterizzazione del modulatore ottico, si è proceduto collegando la sorgente
WDM ad un accoppiatore direzionale, utilizzato come strumento di misura. Per
valutare la caratteristica, si è variata la tensione continua 𝑉𝑏𝑖𝑎𝑠 del dispositivo e si è
misurata la potenza ottica in uscita dal modulatore.
FIGURA 43
La figura precedente mostra la caratteristica 𝑃𝑜𝑢𝑡 − 𝑉𝑏𝑖𝑎𝑠 misurata a distanza di tempo,
e conferma quanto detto in precedenza.
In seguito si è valutata la corrente in uscita dal fotodiodo installato nel
modulatore in funzione della tensione di polarizzazione. Inoltre si è mandato in
ingresso alla porta 𝑅𝐹 del modulatore, un piccolo segnale, tale da rientrare intervallo
di dinamica lineare del Mach Zehnder.
61
FIGURA 44
Il grafico precedente mostra la caratteristica 𝑃𝑜𝑢𝑡 − 𝑉𝑏𝑖𝑎𝑠 , insieme alla corrente
fotorivelata e al guadagno di piccolo segnale in funzione della tensione di
polarizzazione. Si nota che la corrente del fotodiodo è in quadratura rispetto alla
potenza ottica in uscita dal modulatore, aumenta al diminuire della potenza ottica in
uscita dal Mach Zehnder. Si osservi che il grafico del guadagno di piccolo segnale
rappresenta il modulo della derivata della caratteristica della potenza ottica in uscita
dal modulatore, in quanto la tensione picco-picco di piccolo segnale misurata è sempre
positiva. Inoltre, in corrispondenza dei massimi e dei minimi della potenza in uscita dal
modulatore e della corrente in uscita dal fotodiodo, si ha un minimo valore di guadagno
di piccolo segnale. In questi punti di lavoro si ha un funzionamento fortemente non
lineare del modulatore.
62
FIGURA 45
Dalla Figura 45 è possibile osservare l’andamento della corrente fotorivelata in
funzione della tensione di polarizzazione, per diversi valori di potenza ottica in
ingresso. All’aumentare della potenza ottica, si ottengono valori di corrente in uscita
dal fotodiodo, mediamente più elevati.
FIGURA 46
In Figura 46, è riportato un grafico che confronta l’andamento del guadagno di piccolo
segnale e il rapporto tra la potenza della seconda armonica e la potenza della prima
armonica. Si osservi che in corrispondenza del massimo valore del guadagno di piccolo
63
segnale si ha una minima distorsione di non linearità introdotta dalla seconda
armonica di segnale.
FIGURA 47
La curva blu in Figura 47 mostra la caratteristica della corrente in uscita dal fotodiodo
in funzione della tensione di polarizzazione, in seguito ad una leggera pressione
esterna sul modulatore. Si osserva anche in questo caso, un evidente spostamento
della caratteristica.
Di seguito viene spiegato il funzionamento di un algoritmo che permette di ottenere un
controllo automatico della tensione di polarizzazione del modulatore. L’obiettivo è
rendere la tensione di polarizzazione stabile, in modo da avere un punto di lavoro fisso
in corrispondenza del punto di massima linearità di funzionamento del Mach-Zehnder.
L’idea alla base è stata quella di misurare l’uscita in corrente del fotodiodo del
modulatore al variare della tensione di polarizzazione e di modificare la tensione di
polarizzazione in modo da fissare il punto di lavoro in corrispondenza del massimo
valore della derivata prima della caratteristica 𝐼𝑃𝐷 − 𝑉𝑏𝑖𝑎𝑠 . Per implementare tale
sistema si è fatto uso di un kit di sviluppo 𝑃𝑆𝑜𝐶 (𝑃𝑟𝑜𝑔𝑟𝑎𝑚𝑚𝑎𝑏𝑙𝑒 𝑆𝑦𝑠𝑡𝑒𝑚 − 𝑜𝑛 −
𝐶ℎ𝑖𝑝) 5𝐿𝑃 di 𝐶𝑦𝑝𝑟𝑒𝑠𝑠; in generale lo schema di riferimento è il seguente.
Si è impostata una tensione di polarizzazione iniziale. Successivamente si è misurata
una stima della pendenza della caratteristica intorno al valore di tensione impostato
64
inizialmente, valutando l’incremento in corrente tra la corrente misurata nel punto di
lavoro iniziale e la corrente misurata per valori di tensione di riferimento vicini,
equidistanti intorno al valore di tensione di riferimento impostato in precedenza. In
questo modo si ottiene il valore della derivata discreta destra e sinistra rispetto al
punto di lavoro. Da un confronto tra i valori assoluti degli incrementi in corrente, è
possibile scegliere come spostare il punto di lavoro verso il punto di massima derivata.
Iterando i passaggi precedenti, scegliendo come tensione di polarizzazione iniziale
l’ultimo valore della tensione di riferimento assunto in seguito allo spostamento verso
il punto di derivata massima, l’algoritmo converge ad un preciso valore di tensione.
FIGURA 48
La Figura 48 mostra l’andamento nel tempo della tensione di polarizzazione ottenuta
con il metodo descritto in precedenza, su un intervallo di tempo di due ore. Raggiunto
un valore di saturazione, il punto di lavoro subisce scostamenti non trascurabili, che
potrebbero essere dovuti ad errori nel calcolo delle derivate discrete a destra e a
sinistra del valore di tensione di riferimento.
65
Conclusioni
Si sono analizzati i principali componenti di un sistema optoelettronico di
distribuzione di clock per l’esperimento TOTEM all’LHC del CERN, confrontando i dati
sperimentali con le caratteristiche teoriche di ciascun dispositivo. In particolare, si è
posta l’attenzione sulle proprietà fondamentali del modulatore ottico utilizzato nel
sistema di distribuzione. Si è reso evidente il problema della polarizzazione di tale
dispositivo, mostrando la necessità di un sistema in grado di stabilizzare il punto di
lavoro del modulatore, e implementando un possibile algoritmo di controllo
automatico della tensione di polarizzazione. Ciononostante, servirebbe un sistema in
grado di stabilizzare la tensione di riferimento senza perturbare eccessivamente il
modulatore stesso.
66
Bibliografia
[1] Agrawal G.P., Fiber-Optic Communication Systems, New York, Wiley-Interscience,
2002
[2] Chiaradia M.T., Guerriero L., Selvaggi G., Fisica II – Onde Elettromagnetiche, Bari,
Adriatica Editrice, 2003
[3] Ghatak A., Thyagarajan K., Introduction to fiber optics, Cambridge University Press,
1998
[4]Hawkes J., Wilson J., Optoelectronics an introduction, Prentice Hall Europe, 1998
[5] Quinto M., Design Development and Characterization of 2𝑛𝑑 Level Trigger System
for Very Forward Detector at LHC, Dipartimento Interateneo di Fisica “M. Merlin”,
Università degli Studi di Bari “Aldo Moro”, 2014
67