Induzione Magnetica ⇒ Legge di Faraday
Lezione 8
(oltre i campi elettrostatico, magnetostatico, e le correnti stazionarie)
Variazione nel tempo del campo B:
generazione di corrente indotta in circuiti secondari
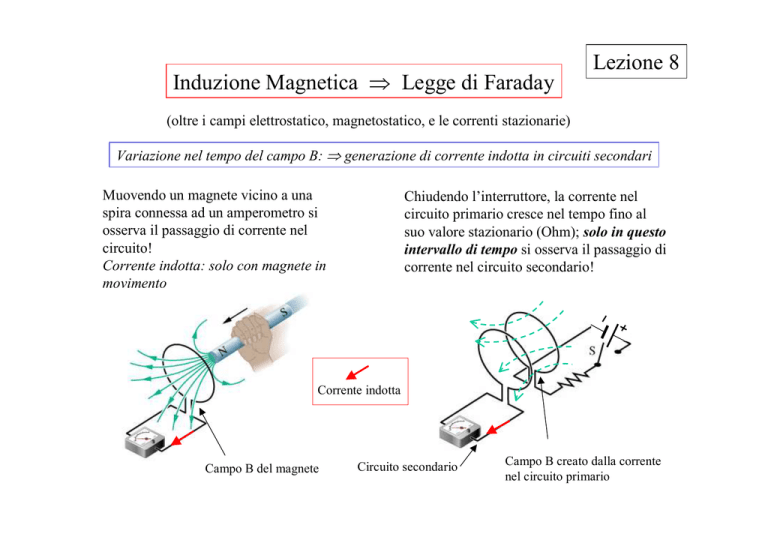
Muovendo un magnete vicino a una
spira connessa ad un amperometro si
osserva il passaggio di corrente nel
circuito!
Corrente indotta: solo con magnete in
movimento
Chiudendo l’interruttore, la corrente nel
circuito primario cresce nel tempo fino al
suo valore stazionario (Ohm); solo in questo
intervallo di tempo si osserva il passaggio di
corrente nel circuito secondario!
Corrente indotta
Campo B del magnete
Circuito secondario
Campo B creato dalla corrente
nel circuito primario
Legge di Faraday: variazione nel tempo di B generazione di forza
elettromotrice indotta (f.e.m.), o di campo elettrico indotto , anche nel vuoto
corrente indotta in circuiti (Ohm etc.)
circuito C
r
n
Formulazione matematica
(di Maxwell)
Derivata temporale totale del flusso
del campo magnetico B su S
ε
r
B
ds
r r
Φ B = ∫ B ⋅ n ds
dΦ B
= −
dt
S
S
Flusso di B attraverso una
qualunque superficie S
concatenata al circuito C
(∝ numero linee di forza)
r
n
r
B
circuito C
Forza elettromotrice
sul circuito C
Segno negativo!
(Legge di Lenz; anche
connessione alla regola
della mano destra)
r
n
S
Superficie S qualsiasi
che ha per bordo C
Forza elettromotrice indotta: integrale del campo elettrico indotto su circuito
chiuso qualunque, anche nel vuoto (circuitazione di E )
ε = ∫ E ⋅ dl (≠ 0)
C
+ A
B
Circuito C
(secondario)
ε
Esempio:
spira aperta
Flusso di B variabile
nel tempo
f.e.m. di un generatore =
differenza di potenziale
(lavoro del campo elettrostatico Es)
ε
∫E
B
= V A − VB =
s
⋅ dl
A
A
+
ε
∫E
Es
(interno)
B
Campo elettrostatico su circuito chiuso:
⋅ dl = 0
Il campo elettrico indotto (dalla variazione di B)
non è conservativo! Il lavoro del campo su
circuito chiuso è diverso da zero!
Campo elettrico
indotto
s
Solo il campo elettrostatico è conservativo
(derivabile da un potenziale)
Campo conservativo
circuitazione nulla!
C
Legge di Lenz:
(il segno negativo)
Il verso della f.e.m. indotta è tale da produrre una corrente
che, a sua volta, crea un campo B che si oppone alla
variazione del flusso di B concatenato col circuito
Campo B creato dalla
corrente indotta
I
Campo B del magnete
m
Esempio: il magnete si muove verso la spira; il flusso di B attraverso la superficie concatenata a C aumenta (entrano
più linee di forza); si produce la corrente indotta I , diretta come in figura, che crea un campo B secondo il teorema
di Ampere. Questo campo è diretto opposto al precedente e tende quindi a contrastare l’aumento del flusso.
Se il magnete si allontana dalla spira C: la corrente indotta ha direzione opposta al caso precedente, quindi ……
La legge di Lenz è connessa alla conservazione dell’energia: se valesse il segno positivo, forza elettromotrice e
campo magnetico si alimenterebbero a vicenda crescendo senza limiti, e creando energia dal nulla.
Spira piana con campo magnetico uniforme
Flusso concatenato Φ B = ∫ B ⋅ n ds = ∫ B cosθ ds = B S cos θ
S
f.e.m. indotta
ε
spira
r
n
S
dΦ B
d
= −
= − (BS cosθ )
dt
dt
θ
r
B
ds
S
corrente indotta
Quindi in un circuito la forza elettromotrice può essere indotta:
a) variando nel tempo il campo magnetico B(t)
b) variando la superficie del circuito S(t)
c) variando l’angolo tra B e la normale alla superficie del circuito θ(t) (rotazione spira)
Analisi dimensionale (unità di misura): per il flusso del campo magnetico (campo·superficie)
si usa spesso il Weber: 1 Weber = 1 T · 1 m2
[ ] = [f.e.m.] = V ( volt)
dΦ B
flusso
Weber T ⋅ m2 Ns m2 J
=
=
=
=
⋅
= =V
s
dt
tempo
s
Cm s
C
La legge di Faraday non necessita di costante dimensionale (ma di costante numerica? …. a dopo!)
Caso b): conduttori in movimento in campo magnetico e bilancio energetico
Fext = − F1
ΦB = B ⋅ L ⋅ x
I
Modulo della f.e.m indotta:
ε
= dΦ B dt = B ⋅ L ⋅ v
I
La corrente indotta è diretta come in figura (legge di
Lenz) per contrastare la diminuzione di ΦB, e vale
R
=
BLv
R
F = I ∆l × B
Il campo B agisce sui conduttori con forze date dalla II legge di Laplace
I=
F1 = I L B; F2 = I x B; F3 = I x B nelle direzioni specificate dal prodotto vettore (vedi figura)
F2 e F3 si equilibrano; la forza F1 si oppone alla forza applicata esterna Fext ; se v costante è F1 = Fext
Potenza della forza esterna (lavoro fatto da Fext nell’unità di tempo): Pext = Fext ⋅ v = ILB ⋅ v =
Potenza dissipata nella resistenza: P = R ⋅ I 2 =
B 2 L2 v 2
R
B 2 L2 v 2
R
uguale alla precedente!
Trasformazione energia meccanica
energia termica per mezzo di legge di Faraday
(correnti di Foucault o correnti parassite – riscaldamento per induzione – etc.)
I
Flusso del campo, in diminuzione nel tempo:
La spira rettangolare (di resistenza R) si muove con
velocità di modulo v = dx/dt costante uscendo dalla
regione limitata di spazio in cui è presente il campo B
Induttanza L
L (di una spira, di un circuito, di una bobina):
rapporto tra il flusso di B concatenato al
circuito, e la corrente I che genera B.
E’ una proprietà geometrica del circuito.
(Induttanza: accumulo flusso di campo B)
Analogia con la definizione
di capacità (anche essa
proprietà geometrica):
ΦB
L=
I
C=
Q
∆V
Capacità: accumulo cariche
Unità di misura: 1 H = 1 Weber = 1 T ⋅ 1 m ( = 1 Ω ⋅ 1 s)
1A
1A
Henry (H)
2
I
B = µ0 n I
n=
Solenoide di lunghezza l , con N spire
circolari di raggio r , percorse da corrente
Induttanza di un solenoide
r
B
N
l
l
N2
Flusso di B concatenato al solenoide Φ B = N ⋅ B ⋅ π r = µ0π r I
l
2
Induttanza del solenoide circolare:
L=
µ0 π r 2 N 2
l
2
2r
f.e.m. autoindotta
I (t )
Per la legge di Faraday - Lenz, se la corrente I varia nel
tempo, si genera un campo B(t) all’interno dell’induttanza,
L = ΦB / I , il quale a sua volta genera una f.e.m εL(t) che
si oppone alla variazione di corrente:
εL =
dΦ B
dI
= −L
dt
dt
ε
−L
dI
− RI (t ) = 0
dt
(equazione differenziale per I(t) analoga a quella per il circuito RC)
I (t ) =
(
1− e
R
=
(
1− e
R
− tR / L
ε
Costante di tempo
τL = L/ R
del circuito RL:
corrente stazionaria ε/R
Soluzione con condizione
iniziale I(0) = 0 :
R
+
L − RI ( t ) = 0
+
I (t )
L
+
L
Chiudendo l’interruttore al tempo iniziale t = 0 : equazione della maglia
Circuito RL
εL(t)
−
εL(t)
−t /τ L
)
)
0
Potenza sviluppata
dal generatore
Energia immagazzinata in una induttanza
Moltiplicando per I l’equazione della maglia,
e utilizzando la conservazione dell’energia:
PL = L I
dI
dt
I = LI
Potenza accumulata
nell’induttanza (per la
creazione del campo B)
Energia totale immagazzinata nell’induttanza
(dalla chiusura del circuito ): proporzionale E
L
alla corrente stazionaria finale al quadrato!
Energia magnetica accumulata nell’induttanza,
ovvero lavoro necessario per creare il campo
magnetico nell’induttanza (o induttore):
=
Potenza dissipata
nella resistenza
∫ P dt = ∫
t →∞
t →∞
L
0
EB =
0
1
dI
dt = L ∫ I dI = L I 2
LI
2
dt
0
uB =
1 2
EB 1 L I 2 1 µ0 π r 2 N 2 I 2 1
=
=
= µ0 n 2 I 2 =
uB =
B
2
2
2 µ0
Vol 2 Vol 2 l ⋅ π r ⋅ l
I
1 2
LI
2
Densità di energia del campo magnetico
In un solenoide (di volume Vol = π r2 · l) B
è praticamente confinato all’interno, quindi
la densità dell’energia magnetica è:
dI
+ RI 2
dt
1
2 µ0
B2
In parallelo alle
formule analoghe
per l’energia
accumulata nel
condensatore e la
densità di energia
del campo
elettrico uE
Lezione 9
Induttanze in serie e in parallelo
serie
ε1
ε2
=
I
1
+
dI
dI
dI
= − L1
− L2
= −(L1 + L2 )
dt
dt
dt
2
L2
L1
Leq = L1 + L2
induttanza equivalente
Leq
I
ε
I1
L1
I
L2
I2
ε
Leq
=−
1
1 1
= +
Leq L1 L2
Leq =
dI
d ( I1 + I 2 )
=−
= +
dt
dt
L1 L2
parallelo
L1 L2
L1 + L2
Moto di una carica in campo magnetico: forza di Lorentz
Fl
B
Tratto di conduttore percorso da corrente I,
e immerso in B; su di esso agisce la forza F
Fl = I l × B
S
vd
La corrente è costituita da N cariche q per unità di
I = N q S vd
volume in moto con velocità di deriva vd (Lez. 4)
F = Fl /( N ⋅ S ⋅ l )
l
Forza sulla singola particella carica:
I
r
r r
Forza di Lorentz F = q v × B
LB = ∫ F ⋅ d s = ∫ F ⋅ ( v dt ) = 0
v
B
v
F
P
B
Q
Q
F
È la forza esercitata dal campo magnetico B su cariche
elettriche in movimento (N.B. se v = 0, la forza è nulla!)
Lavoro della forza di Lorentz, o lavoro del
campo magnetico su particelle carica;
poichè F è sempre perpendicolare a v :
P
Il lavoro delle forze magnetiche è sempre nullo!
L’energia cinetica delle particelle cariche si conserva.
(modulo
F = q v B senθ )
La forza magnetica agisce come forza centripeta (perpendicolare alla
velocità) quindi la particella percorre traiettorie circolari o elicoidali.
Esempio: se la velocità della particella forma un angolo φ con la direzione z
del campo B , la forza ha modulo F = q v B senφ = qBv ⊥
cioè dipende solo dalla componente di v perpendicolare a B , e giace sul piano
x-y. Quindi agisce da forza centripeta costringendo la particella a un moto
circolare sul piano x-y, che si compone col moto rettilineo uniforme in
direzione z (infatti la componente su z della velocità rimane invariata).
Si ha così un moto a elica, che si avvolge intorno a B.
Esempio: le particelle cariche che viaggiano verso la Terra vengono
“catturate” dal campo magnetico e orbitano a spirale intorno alle linee di
forza di B , entrando nell’atmosfera nei pressi del polo Nord (aurore boreali)
z
x
y
B
F
Passo dell’elica
B
Spettrometro di massa: misura della massa di uno ione
F
v2
qv B = m⋅
r
v2
F = m ⋅ ac = m ⋅
r
Lo ione di carica +q e massa m viene accelerato da un campo
elettrostatico fino alla velocità v, entra nella regione dove vi è il
campo magnetico B (perpendicolare) e percorre la traiettoria
circolare di raggio r fino a colpire la lastra fotografica alla distanza
x=2r dall’ingresso. Si determina quindi la sua massa.
m=
qBr
v
Relazione tra forza di Lorentz e legge di Faraday
+
B
F
I
E
∆V
q E = q v0 B
1) Azione della forza (cariche in movimento)
Una sbarretta conduttrice di lunghezza l scorre con velocità
v0 su due guide fisse; sulle cariche libere presenti in essa
agisce la forza di Lorentz
F = qv×B
e le cariche positive tendono ad accumularsi ad una estremità.
Si genera quindi un campo elettrico E (tratteggiato in figura)
in direzione opposta alla forza . Si avrà equilibrio quando la
forza di Lorentz sarà uguale alla forza elettrica qE, cioè
()
R
E = v0 B
Alle estremità della sbarretta si ha una differenza di potenziale
∆V = E ⋅ l = B ⋅ l ⋅ v 0
-
Se le guide sono conduttrici e vi è una resistenza R , la sbarretta
funge da generatore per il passaggio di corrente I nel circuito.
2) Legge di Faraday (flusso magnetico in movimento)
La sbarretta conduttrice “taglia” il flusso del campo magnetico
(che quindi aumenta nella superficie spazzata), quindi si
genera una f.e.m. indotta di modulo
ε = dΦdt
B
=
d
(B ⋅ l ⋅ x ) = B ⋅ l ⋅ d x = B ⋅ l ⋅ v 0
dt
dt
che induce nel circuito una corrente I diretta in modo da
contrastare l’aumento del flusso del campo magnetico. Lo
stesso risultato vale se la sbarretta è ferma e a muoversi è il
campo magnetico (verso sinistra).
Le due descrizioni sono
diverse ma portano allo
stesso risultato!
C’è quindi una relazione
profonda tra le due leggi
(si va verso il principio di
relatività di Einstein)
x
m
B
Dipolo magnetico da moto orbitale
dell’elettrone in un atomo: e si muove in
orbita circolare intorno al nucleo:
momento angolare L, e momento
magnetico m (l’elettrone si può
considerare come una corrente di cariche
negative! e per il teorema di Ampere ……)
e
−I
Magnetismo e materia
m
Dipolo magnetico o momento
magnetico: rappresentato dal
vettore m , genera un campo
magnetico B come in figura.
Campo B
da moto orbitale
B
I materiali magnetici devono le
loro proprietà al moto (orbitale o
intrinseco) degli elettroni; infatti
vi sono due contributi al loro
momento magnetico (e quindi al
campo B interno associato)
L’elettrone (come le altre particelle
elementari) possiede un momento
magnetico intrinseco m , associato
s
al momento angolare intrinseco detto
spin (si può pensare all’elettrone in
rotazione attorno al proprio asse).
ms
Campo B da momento
magnetico intrinseco
Materiali diamagnetici
(semplificando) In un atomo, il numero di elettroni che orbitano in un
senso eguaglia quello degli elettroni che orbitano in senso opposto; il
momento magnetico totale è nullo. Quando si applica un campo B
esterno, il moto elettronico varia e il materiale tende a respingere B
sviluppando un dipolo magnetico opposto.
Bext
Materiali paramagnetici
m =0
Allineamento,
magnetizzazione non nulla
m ≠0
Orientamento casuale,
magnetizzazione nulla
Atomi (o molecole) hanno un momento magnetico
risultante non nullo, orientato casualmente. In presenza di
campo B esterno si ha tendenza all’allineamento dei dipoli
magnetici, con un momento magnetico totale
macroscopico. Il materiale è detto magnetizzato (analogia
con la polarizzazione elettrica)
Materiali ferromagnetici
Configurazione dei domini magnetici in Nickel
In questo caso, in media,
m =0
Allineamento spontaneo di dipoli magnetici atomici
su grande scala (effetto quantistico); formazione di
“domini magnetici”, generalmente cristalli
microscopici. Se i domini sono ben allineati (dipende
dalla temperatura) si ha il ferromagnete o magnete
permanente (calamita: ferro,nichel etc.) che possiede
un campo magnetico proprio.