Esercizi sui fluidi II

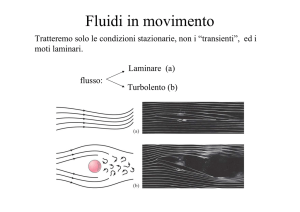
Modulo di Elementi di Fluidodinamica
Corso di Laurea in Ingegneria dei Materiali/Meccanica
A.A. 2004/2005
Ing. Paola CINNELLA
ESERCIZI SVOLTI DI FLUIDODINAMICA
Parte 3: Equazione di Bernoulli
Versione 1.0
Esercizio 1_______________________________________________________________________
Si consideri un serbatoio dotato di un’apertura circolare di diametro d. Si vuole confrontare la
portata uscente dal serbatoio nel caso in cui sia presente la sola apertura e nel caso in cui
quest’ultima sia collegata ad un tubo verticale di lunghezza L (vedere la figura 4.1). Si consideri il
fluido come ideale.
1. Determinare nei due casi la velocità del liquido ad una distanza verticale L dall’uscita del
serbatoio, posto che il pelo libero del serbatoio sia posto ad un’altezza h rispetto al fondo.
Trascurare l’abbassamento del pelo libero con lo svuotamento.
2. Qual è la velocità del liquido nella sezione di uscita del serbatoio nei due casi ?
3. Dedurne la portata uscente nell’uno e nell’altro caso. Qual è il dispositivo più efficace ?
4. Qual è la lunghezza massima che può avere il tubo di uscita senza che si produca cavitazione ?
Quanto vale la portata per tale valore ?
DATI. : h = 5 m ; d = 20 cm ; pressione di vapore del liquido a 20°C = 2,34 kPa.
h
d
d
L
- figura
41
________________________________________________________________________________
1. Applichiamo l’equazione di Bernoulli ad una traiettoria che va da un punto A situato vicino al
pelo libero del serbatoio ad un punto L situato verticalmente al di sotto dell’apertura, ad una
distanza L da questa.
Caso 1:
p A VA2
p V2
+
+ g ( H + L ) = L + L (1)
2
2
ρ
ρ
In questa espressione, pA=pL=patm, e VA≈0. Se ne deduce che
VL = 2 g ( H + L ) .
1
Caso 2. L’equazione di Bernoulli scritta tra il pelo libero del serbatoio e un punto L
all’uscita del tubo si scrive esattamente come prima (1) e si ha ancora pA=pL=patm. Ne
deduciamo che le due velocità sono identiche.
2. Stavolta scriviamo l’equazione di Bernoulli tra un punto prossimo al pelo libero ed un punto B
situato nella sezione di uscita del serbatoio.
Caso 1.
p A VA2
pU VU2
+
+ g (H + L) =
+
+ gL (2)
ρ
2
ρ
2
dove pA=pU=patm, e VA≈0. Ne deduciamo che
VL = 2 gH
Caso 2.
L’equazione di Bernoulli non cambia, ma stavolta il punto U non si trova a pressione
atmosferica. Infatti, per l’equazione di continuità, nel condotto la velocità deve essere
costante, dato che il fluido è incomprimibile e la sezione è costante. Si ha dunque VU= VL.
Dove VL è stata calcolata precedente mente. La velocità di efflusso dal serbatoio è dunque
maggiore nel caso 2.
3. Le portate di efflusso nei due casi sono
d2
d2
Q1 = π
2 gH ; Q2 = π
2g (H + L)
4
4
Il dispositivo più efficace è dunque il secondo.
4. Applichiamo l’equazione di Bernoulli tra l’ingresso e l’uscita del condotto. Troviamo:
pU VU2
p V2
+
+ gL = L + L (3)
2
2
ρ
ρ
dove VU= VL, da cui pU = pL − ρ gL = patm − ρ gL . La sezione di ingresso del condotto è dunque a
rischio di cavitazione. Si ha incipiente cavitazione se la pressione del punto U uguaglia la pressione
di vapore dell’acqua alla temperatura di esercizio del sistema (supposta pari a 20°). Posto che la
pressione atmosferica sia pari ad 1bar, la lughezza massima del tubo prima che sia abbia cavitazione
si ottiene ponendo:
( patm − pvap ) = 9.96 m
pU = patm − ρ gL = pvap ⇒ L =
ρg
In questo caso la portata vale:
d2
Q2 = π
2 g ( H + L ) = 0.538 m3.
4
Esercizio 2_______________________________________________________________________
Il dispositivo rappresentato in
A
2,5 mm
D
figura 4.2 deve disperdere una miscela
acqua
acqua
d’acqua e di insetticida. La portata di
+
insetticida deve essere pari a Qi = 75
insetticida
-1
ml.min mentre la portata d’acqua è Qa = 15 cm
0,4 mm
4 l.min-1. Calcolare, in tali condizioni, il
insetticida
valore della pressione nel punto A e il
diametro D del dispositivo.
________________________________________________________________________________
2
Applichiamo l’equazione di Bernoulli tra un punto I situato nel condotto di estrazione
dell’insetticida, all’altezza del pelo libero, e il punto A:
p A VA2
p V2
+
+ gH = I + I
2
2
ρ
ρ
dove H rappresenta la distanza tra il peo libero del serbatoio ed il punto A. Nell’ipotesi che
l’insetticida nel serbatoio sia praticamente in quiete, VI≈0 e l distribuzione delle pressioni è
idrostatica, per cui la pressione pI uguagli la pressione del pelo libero, ovvero quella atmosferica. La
velocità dell’insetticida nel punto A, all’uscita del condotto di estrazione, può essere dedotta dalla
portata di insetticida e dai dati geometrici del condotto:
d2
Qi = VA,iπ
ÆVA,i=9.95 m/s
4
Pertanto, la pressione relativa del punto A è: pA=-0.495 bar.
Calcoliamo la portata che fluisce attraverso il dispositivo. La portata uscente da quest’ultimo è la
somma della portata di acqua più quella dell’insetticida. La velocità della miscela all’uscita del
dispositivo può essere ricavata dalla relazione:
Du2
Qi + Qa = Vuπ
ÆVu=13.8 m/s
4
Se adesso applichiamo l’equazione di Bernoulli alla traiettoria di una particella d’acqua che si
sposta da un punto subito a monte di A (dove il fluido che scorre nel dispositivo è solo acqua
all’uscita, abbiamo:
2
p A VA,a pu Vu2
+
=
+
,
ρ
ρ
2
2
e da questa possiamo ricavare la velocità dell’acqua subito a monte del punto A:
VA,a=17.0 m/s
Nota tale velocità, possiamo finalmente calcolare il diametro D dalla relazione:
D2
Qa = VA, aπ
ÆD=2.23mm.
4
Esercizio 3_______________________________________________________________________
Un tubo di Pitot viene immerso in un fluido che scorre con velocità v. Se tale fluido è aria e il
liquido manometrico contenuto nel tubo è acqua, determinare la velocità del fluido quando la
differenza di altezza del liquido manometrico è h=0.65 cm.
(Per la densità dell'aria usare ρaria =1.29 kg/m³)
__
Applichiamo l'equazione di Bernoulli ai punti a e b (vedere figura), dove b si suppone sia il punto di
arresto del fluido e ρ la sua densità:
.
3
Del resto, se h è la differenza di altezza del liquido nei due rami del manometro e ρ’ la sua densità,
possiamo scrivere:
.
Confrontando le due equazioni, si ricava per la velocità dell'aria l'espressione:
.
Sostituendo i relativi valori delle densità, dell'altezza e dell'accelerazione di gravità, si trova infine il
valore cercato della velocità:
v=0.31 m/s
Esercizio 4_______________________________________________________________________
Nell’ipotesi di liquido perfetto (γ=8825 N/m3), calcolare la portata Q del sifone in figura.
Individuare inoltre il massimo valore della portata scaricabile dal sifone, al variare della quota della
sezione di sbocco.
Dati: h=2m, diametro del sifone:D=0.075m, H=3m
1. Applichiamo innanzi tutto l’equazione di Bernoulli tra il pelo libero del serbatoio (punto A)
e la sezione di uscita (punto S). In ambo i punti regna la pressione ambiente (pressione
relativa nulla). Avremo dunque:
p
V2
p A VA2
+
+ z A = S + S + zS
γ
2g
γ
2g
dove abbiamo assunto il pelo libero del serbatoio come quota di riferimento (zA=0) e dove zs=H. Se ne ricava una velocità di efflusso pari a:
VS = 2 gH = 7.67 m/s
e dunque una portata scaricata pari a:
D2
Q = VS π
= 33.9 l/s .
4
4
2. Consideriamo adesso che la quota H dello scarico del sifone rispetto al pelo libero del
serbatoio possa variare. Dato che VS = 2 gH , ci aspettiamo che all’aumentare di H aumenti
la velocità di efflusso e dunque la portata scaricata. La quota H non può tuttavia essere
aumentata indefinitamente. Infatti la pressione assoluta nel punto più alta del serbatoio, data
da (applicando Bernoulli tra il punto M e il punto S e tenendo conto che, per la
conservazione della portata, VS=VM):
pM = pa − γ ( H + h )
non può divenire negativa. Il massimo valore ammissibile di H sarà dunque quello per cui
nel punto M la pressione si annulla:
p
H max = a − a = 9.47 m ,
γ
dove si è assunto pa=pressione ambiente=1 atm. Noto Hmax possiamo calcolare la portata
corrispondente:
D2
Qmax = 2 gH max π
= 60.2 l/s .
4
In realtà, il massimo valore ammissibile a quello trovato: infatti a partire dal momento in cui
la pressione pM uguaglia la tensione di vapore dell’acqua alla temperatura di esercizio
insorgeranno fenomeni di cavitazione (vaporizzazione dell’acqua) che limiteranno
ulteriormente la possibilità di abbassare la sezione di sbocco del sifone.
5