Termodinamica: concetti di base
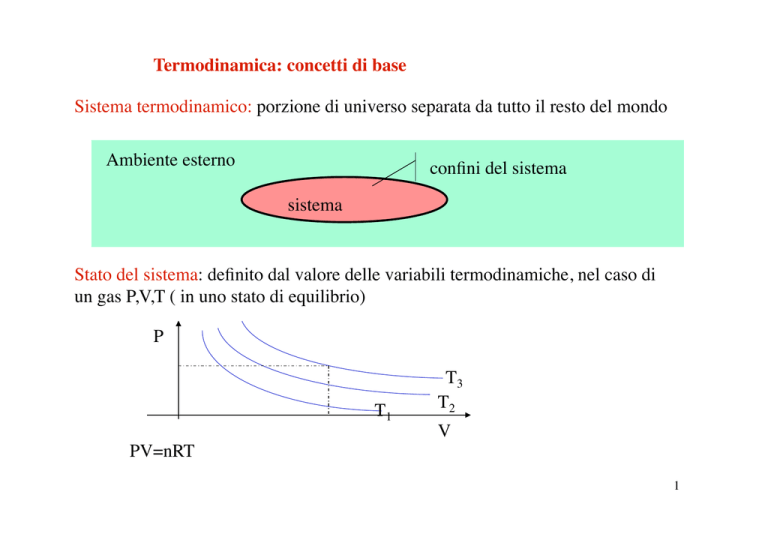
Sistema termodinamico: porzione di universo separata da tutto il resto del mondo
Ambiente esterno
confini del sistema
sistema
Stato del sistema: definito dal valore delle variabili termodinamiche, nel caso di
un gas P,V,T ( in uno stato di equilibrio) P
T1
T3
T2
V
PV=nRT
1
Trasformazione: passaggio da uno stato ad un altro per intervento dell’ambiente
esterno (il sistema in uno stato di equilibrio non cambia spontaneamente)
Trasformazioni reali o irreversibili:il percorso della trasformazione ?? (solo stato di
equilibrio di partenza stato di equilibrio di arrivo) e non può essere percorsa in senso
inverso
A
P
B
V
Trasformazioni ideali o reversibili:inesistenti in natura
• successione continua di stati di equilibrio
• compiute in un senso e in senso contrario non lasciano tracce nell’ambiente Trasformazioni quasi statiche: avvengono lentamente da poter essere
considerate come sequenza di stati di equilibrio. Perché possano essere
considerate reversibili occorre ridurre il più possibile fenomeni dissipativi e
che gli scambi di calore avvengano tra corpi con una differenza piccola di
temperatura (limite ⇒0)
2
Isoterme
T costante
P
ramo d’iperbole
V
Isobare
P costante
P
V
Isocore
Adiabatiche
V costante
Q=0
P
P
V
V
3
cicliche
A ad A
P A
V
Espansione libera
Trasformazione irreversibile NON ha una
rappresentazione grafica
Funzioni di stato
Se la grandezza G è una funzione di stato, allora ad ogni stato del sistema
corrisponde un ben determinato valore della grandezza G;
G=f(stato)
• La sua variazione dipende solo dallo stato iniziale e finale e non dalla
trasformazione seguita (ad esempio nel caso di un gas la pressione P)
• Viceversa, se una certa quantità è indipendente dalla trasformazione, ma
dipende solo dallo stato iniziale e finale, allora quella quantità può essere
interpretata come la variazione di una funzione di stato
Sono funzioni di stato l’energia interna e l’entropia di un sistema 4
Scambi energetici tra sistema e ambiente esterno
Lavoro e/o calore modi di fare lavoro⇔forze che possono essere esercitate su o da un sistema
Lavoro ⇒variazione di volume
nel caso di un gas si ha lavoro in corrispondenza di un cambiamento di volume
h
F
h
F
Espansione L>0
Compressione L<0
Nel caso di un lavoro positivo si ha diminuzione di energia interna del sistema,
se la trasformazione è adiabatica il sistema si raffredda L=FΔx=PAΔx=PΔV
5
P
P
P1
P
P1
P1=P2
P2
P2
V1
V2
V
V1
V2
V
V
Isoterma
Isobara
Isocora
L=nRT lnV2/V1
L=P(V2-V1)
L=0
Nel caso di un gas:L=area sottesa dalla trasformazione nel piano P-V
Per una trasformazione ciclica il lavoro è dato dall’area racchiusa dal ciclo
6
Energia interna Qual’è l’energia di un bicchiere
di acqua?
Su scala macroscopica il bicchiere
d’acqua sembra non possedere alcuna
energia Il sistema possiede una data energia interna dovuta all’energia cinetica e
potenziale (associata alle forze attrattive) delle molecole Calore si ha scambio di calore tutte le volte che tra sistema ed ambiente
esterno esiste una differenza di temperatura
Q>0 quando è assorbito dal sistema
Q<0 quando è ceduto dal sistema 7
Il Primo Principio della Termodinamica
il Io P. della T. ⇒Conservazione dell’energia totale
Relazione tra Energia Interna_Calore scambiato_Lavoro
Q-L=ΔU
Il calore assorbito - il lavoro fatto dal sistema sull’ambiente • U “energia interna” è una funzione di stato del sistema (ΔU, al contrario di Q ed L,
non dipende dal tipo di trasformazione termodinamica ma solo dal valore che le
variabili termodinamiche assumono allo stato iniziale e finale)
• Si misura in J e si possono misurare solo ΔU
• In un gas perfetto U dipende solo dalla temperatura
• ΔU quantità di energia scambiata tra il sistema e l’ambiente ⇒ conservazione
dell’energia
Nel caso di un sistema isolato (Q=0 e L=0) l’energia interna si deve conservare
U=costante
8
Dal Io P. segue:
• L e Q devono essere trattati nello stesso modo
• Si ottengono ΔU con Q o L o loro combinazioni e sono indipendenti dal
modo con cui si ottengono ΔU=f(Pi,Vi,Ti;Pf,Vf,Tf)
bi
scam
lavoro
Calore
Q=cmΔT
ΔU=Q-W
1cal=4.1868J
Q/t=kAΔT/d
9
Applicazioni del primo principio
• Trasformazione isoterma : in un gas perfetto U è la somma delle energie cinetiche delle molecole
Ecin=3/2KBT
U=N 3/2KBT
E quindi se T non varia anche U non varia ΔU=0 ossia Q-L=0
Q=L
• Trasformazione adiabatica :(Q=0) ΔU=-L
• Trasformazione isocora: (V=cost) L=0
ΔU=Q=cVmΔt
• Trasformazione isobara: (P=cost)
ΔU=cPmΔt-PΔV
• Trasformazione ciclica:
ΔU=0 Q=L
In una trasformazione qualsiasi di un gas perfetto
ΔU=nCV(T2-T1) Cv calore molare a volume costante
10
Il secondo principio della Termodinamica
Il I P. NON permette di prevedere il rapporto tra il lavoro fatto e il calore fornito
Il II P. limita le possibilita` di scambio di calore e del suo impiego come energia
meccanica (lavoro). Permette di calcolare il rendimento di una macchina termica
ideale. T1=cost >T2
Una macchina termica deve compire un
ciclo e tornare al proprio stato
termodinamico iniziale (ΔU=0) dopo aver
scambiato calore e lavoro con l’ambiente
esterno
Q1
L
Q2
T2=costante
η=
Q − Q2
Q
L
= 1
= 1− 2
Q1
Q1
Q1
ηrev = 1 −
T2
T.di Carnot
T1
11
€
I due enunciati del II P.
• Kelvin-Planck: è impossibile realizzare una macchina che lavorando
ciclicamente, trasformi in lavoro meccanico il calore scambiato con un’unica
sorgente (non è possibile come unico risultato estrarre calore da un’oggetto e
convertirlo interamente in lavoro)
• Clausius: è impossibile realizzare una macchina che lavorando ciclicamente
abbia come unico risultato il passaggio di una certa quantita` di calore dalla
sorgente fredda a quella calda (il calore non fluisce MAI spontaneamente da
una sorgente fredda ad una piu` calda)
12
€
Teorema di Carnot Il T. di Carnot stabilisce che date due sorgenti di
calore alle temperature T1 e T2 < T1, tutte le
T2
ηrev = 1 −
macchine termiche reversibili funzionanti con le
T1
due sorgenti hanno lo stesso rendimento ηrev
mentre ogni altra macchina irreversibile che
funzioni con le stesse sorgenti ha un rendimento
η< ηrev
13
€
Interpretazione del II P.
-microscopica: i sistemi tendono ad evolvere da configurazioni caratterizzate
da un grande ordine verso configurazioni più disordinate e più probabili
-macroscopica: una certa grandezza (funzione di stato) detta ENTROPIA (S)
tende ad assumere il massimo valore possibile dQ è la quantita` di calore scambiata con il sistema a
dQrev
dS =
temperatura T
T
Entropia totale (del sistema e dell’ambiente)
ΔS ≥ 0
non può mai diminuire ; ΔS=0 nel caso di
o
ΔS si misura in J/ K
trasformazioni reversibili e ΔS>0 nel caso di
trasformazioni irreversibili
Si può dimostrare l’equivalenza con i precedenti enunciati del II P.
14
B
Dalla definizione di variazione di entropia ΔS = SB − SA =
∫
A
dQrev B dQ
>∫
T
A T
Segue che se la trasformazione è adiabatica ossia calore scambiato=0
€
ΔS=0 per una trasformazione adiabatica
reversibile
ΔS>0 per una trasformazione adiabatica irreversibile
Poiche ` si puo` considerare l’universo in cui viviamo un sistema isolato (non c’è
nulla al di fuori con cui scambiare calore) possiamo formulare il IIo pricipio della T.
dicendo che per ogni trasformazione termodinamica deve valere la relazione ΔSu≥0
dove vale l’ugualianza solo per trasformazioni reversibili
Le trasformazioni che avvengono in natura sono sempre irreversibili quindi sono sempre accompagnate da un aumento di entropia dell’universo
15
NB: -Gli unici cambiamenti possibili in un sistema isolato (come l’Universo) sono
quelli per cui ΔS ≥ 0
-In natura le trasformazioni sono sempre irreversibili e quindi producono sempre
un aumento di entropia
-L’entropia dell’universo non puo` mai diminuire, questo non implica che
l’entropia di un singolo elemento dell’universo non possa diminuire, cio` puo`
avvenire purche` per qualche altro componenete dell’universo abbia un aumento di
entropia maggiore
16
Calcolo della variazione di Entropia
• individuare una trasformazione reversibile che colleghi il punto
iniziale A e finale B
B
dQrev
ΔS = SB − SA = ∫
T
A
• nel caso di Gas perfetti si dimostra che :
dQ = dU + dL
€
dL = PdV dU = ncV dT
T
V
ΔS = SB − SA = ncV ln B + nR ln B
TA
VA
• per una trasformazione reversibile isoterma T=cost dove Qrev è
tutto il calore scambiato
€
ΔS = SB − SA =
Qrev
T
ad esempio nel caso di cambiamento di stato
€
ΔS = SB − SA =
λm
T
17
• Nel caso di un corpo di massa m e calore specifico c inizialmente alla temperatura
TA che scambia calore con l’esterno e subisce una variazione di temperatura fino a
TB la variazione di entropia è data dall’espressione: B
ΔS = SB − SA =
∫
A
€
dQrev
=
T
B
∫
A
cmdT
T
= cm ln B
T
TA
• Per calcolare la variazione di entropia dell’Universo occorre sommare la variazione
di entropia dei singoli sistemi che partecipano allo scambio di calore
18
I Potenziali Termodinamici
Funzioni dette ”potenziali termodinamici" utili per descrivere l’evoluzione di
reazioni chimiche e processi non ciclici sono: - l’energia interna U
- L’entalpia H
- L’energia libera di Helmholtz F - L’energia libera di Gibbs G ENERGIA INTERNA U
l’energia interna U rappresenta il calore scambiato dal sistema
in una reazione a Volume costante
Dal Io principio della T. segue che: ΔU=Q - PΔV se V=costante ΔU=Q
19
ENTALPIA
H = U + PV
E` utile per descrivere le trasformazioni che avvengono a pressione P=costante (ad
esempio reazioni chimiche)
ΔH = ΔU + PΔV=ΔU+L=Q la variazione di entalpia è pari al calore scambiato
(assorbito o ceduto) nella trasformazione a pressione costante.
Q ceduto Q<0 ΔH<0 l’entalpia diminuisce
Q assorbito Q>0 ΔH>0 l’entalpia aumenta
H o meglio ΔH rappresenta l’energia termica che il sistema deve scambiare per
compiere una determinata trasformazione a pressione costante.
20
ENERGIA LIBERA (o potenziale ) DI HELMOLTZ
B
T=costante
SB − SA ≥
∫
A
dQ 1
=
T
T
B
Q
∫ dQ = T
A
Q ≤ T(SB − SA )
Per il Io
ΔU = Q − L
€
Principio
L = Q − ΔU ≤ T(SB − SA ) − (U B − U A )
Utile per descrivere le trasformazioni che avvengono a V e T costanti. La variazione:
ΔU = Q − L
€
L = Q − ΔU ≤ T(SB − SA ) − (U B − U A )
L ≤ −ΔF
€
Pone un limite superiore al lavoro che il sistema puo` compiere portandosi dallo stato A
allo stato B.
Nel caso il sistema non compia lavoro (V=costante) L=0 ΔF≤0 FB≤FA indica che il sistema (la reazione) evolve verso stati di energia libera F
decrescente e l’equilibrio si raggiunge per il valore minimo di F 21
ENERGIA LIBERA DI GIBBS
Molto spesso reazioni chimiche avvengono a temperatura e pressione
costante cosi` pure trasformazioni che implicano una transizione di fase.
L’energia libera di Gibbs risulta molto utile per descrivere queste
trasformazioni chimiche e fisiche e gli stati di equilibrio dei sistemi ad
esse soggetti
22
ENERGIA LIBERA DI GIBBS G = U + PV-TS
È utile per descrivere le trasformazioni che avvengono a T e P costante, condizione
in cui avvengono tutte le reazioni chimiche in una cellula.
A P e T costante la variazione ΔG:
ΔG = ΔU + PΔV −TΔS = ΔH −TΔS
In termini di calore scambiato ed usando la relazione tra entropia e calore Qrev
ΔG = Q−Qrev
€
Applicando il IIo P. della Termodinamica €
Qrev Q
≥
T T
Risulta ΔG ≤ 0 il segno di ugualianza vale solo se la trasformazione è reversibile.
Nel caso di reazioni chimiche irreversibili il processo avverra` nella direzione che
riduce G fino a raggiungere, all’equilibrio, il valore minimo.
23
€
€
L ≤ TΔS −ΔU
ΔG = ΔU + PΔV −TΔS = ΔH −TΔS ≤ 0
€
Per un sistema termodinamico a contatto termico con un ambiente a
temperatura T che si trasformi a pressione costante G non puo`
aumentare e gli stati in cui G è minima rappresentano stati di
equilibrio.
La spontaneita` della reazione è legata al segno relativo di ΔH e ΔS
ed al valore di di T.
(vedi tabella i casi in cui ΔG<0)
ΔH
ΔS
ΔH<0 ΔS>0
Reazione spontanea esotermica
ΔH<0 ΔS<0
Reazione spontanea esotermica a T basse
ΔH>0 ΔS>0
Reazione spontanea endotermica a T alte
ΔH>0 ΔS<0
Reazione non spontanea
24
25
Alcune formule per il Gas Perfetto
Equazione di stato per il gas perfetto
PV = nRT
J
R = 8.31
; n = numero di moli
mole ⋅ K
relazione di Mayer per il calore specifico
cp - cv = R
5
7
c p calore specifico a pressione costante (cp = R per gas monoatomici, c p = R per gas biatomici)
2
2
3
5
c v calore specifico a volume costante (cv = R per gas monoatomici, c v = R per gas biatomici)
2
2
c
5
7
γ = p (γ = per gas monoatomici, γ = per gas biatomici)
cv
3
5
differenza di energia interna tra due stati A e B
ΔU = nc v (TB - TA )
differenza di entropia tra due stati A e B
TB
VB
ΔS = nc v ln + nRln
TA
VA
26
€
Alcune trasformazioni del Gas Perfetto
Isocora V = costante L = 0 Q = ΔU = nc v (TB - TA )
PA PB
=
TA TB
Isobara P = costante L = P(VB - VA ) Q = nc p (TB - TA )
VA VB
=
TA TB
Isoterma T = costante L = nRTln
VB
Q=L
VA
PAVA = PBVB
Adiabatica L = -ΔU = −nc v (TB - TA ) Q = 0
PAV Aγ = PBV Bγ
TAV Aγ −1 = TBV Bγ −1
€
27












