ESERCIZIO – Transcaratteristica di circuito con Operazionale e

ESERCIZIO – Transcaratteristica di circuito con Operazionale e
Zener
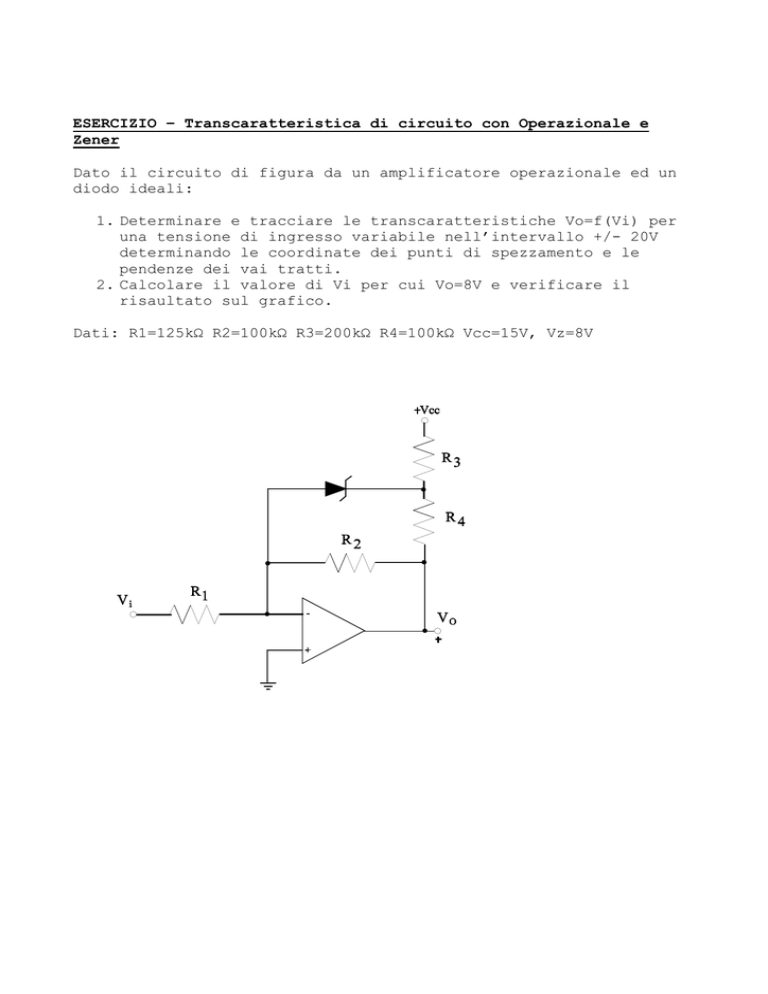
Dato il circuito di figura da un amplificatore operazionale ed un
diodo ideali:
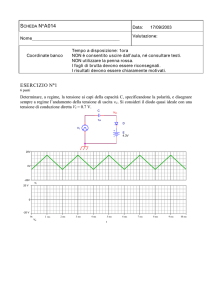
1. Determinare e tracciare le transcaratteristiche Vo=f(Vi) per
una tensione di ingresso variabile nell’intervallo +/- 20V
determinando le coordinate dei punti di spezzamento e le
pendenze dei vai tratti.
2. Calcolare il valore di Vi per cui Vo=8V e verificare il
risaultato sul grafico.
Dati: R1=125kΩ R2=100kΩ R3=200kΩ R4=100kΩ Vcc=15V, Vz=8V
Soluzione
La caratteristica (idealizzata) del diodo zener è:
La transcaratteristica Vo=f(Vi) si compone di tre tratti distinti
per ognuno dei quali cambia il modo di funzionare dello zener. In
particolare:
Zona zener: IZ=-ID>0 VZ=8V
Le correnti sulle quattro resistenze e sul diodo zener dipendono
dalle tensioni di ingresso e di uscita, Vi e Vo, come mostrano le
seguenti relazioni riferite allo grandezze elettriche evidenziate
nello schema

I1



I2




I
3


I4


Vi
Vi

 8 Vi A
R1
125k 
V
VO
 O 
 10 VO A
R2
100k 
V VA
7V
 CC

 35 A
R3
200k 
V VO
8 VO
 A

 80 10 VO A
R4
100k 

Le relazioni scritte tengono conto del fatto che la tensione di
ingresso dell’operazionale ideale, funzionante in zona lineare, è
nulla (massa virtuale); ne segue che il potenziale VA coincide con
la VZ indipendentemente dai valori delle correnti afferenti a
questo nodo.
Peraltro, le correnti sono vincolate tra loro dai seguenti legami
IZ  I3 I4  0 condizione imposta dalla zona zener


I1 IZ I2  0 primo di Kirchhoff

Sostituendo in queste ultime relazioni i precedenti legami di ogni
corrente con le tensioni di ingresso e di uscita si ottiene:
35 80 10 VO  0


I1 
I3 I4 I2  8 Vi 
45 10 VO 10 VO  0

VO  4,5


VO  0,4 Vi 2, 25

Vi  5,625


VO  0,4 Vi 2, 25

in zona zener
Zona off: IZ=0 0<VZ<8V
In questo tratto di caratteristica dello zener la corrente IZ è
nulla per cui le due resistenze R3 ed R4 sono in serie. Il legame
ingresso-uscita,
tra
Vi
e
Vo,
è
tipicamente
quello
dell’amplificatore invertente, come mostra il seguente schema
Valgono quindi le seguenti relazioni:
0  VA  8V condizione imposta dalla zona off dello zener


R2

V


Vi amplificatore invertente
O

R

1
VCC VO

15 VO

0

R4 VO  8V
0

100k  VO  8V


R3 R4


200k  100k 


100k 
R2


VO   Vi
VO  
Vi


R
125
k



1
2

0  5  VO  8V

3


VO  0,8 Vi

5,625  Vi  9,375

VO  0,8 Vi

8

0  5  Vi  8V

15


VO  0,8 Vi

75
 45
 Vi 

8
 8

VO  0, 8 Vi

Zona on: IZ<0 VZ=0
In questo tratto di caratteristica dello zener la corrente IZ è
negativa e la tensione VD è nulla. Il legame ingresso-uscita, tra
Vi e Vo, è quello del sommatore invertente, come illustrano le
seguenti figure
Valgono le seguenti relazioni:


IZ


'
R2



VO




IZ




VO


75


VO

I3 I4  0

condizione imposta dalla zona on dello zener
R2R4
100k  100k 

 50k 
R2 R4
100k  100k 
R'
R'
  2 Vi - 2 VCC
R1
R3
resistenza retroazione
amplificatore sommatore invertente
VCC

V
 O 0
15

VO

IZ 

0
R3
R4

200k  100k 

50k 
50k 

VO  0,4 Vi 3,75

Vi 15V

125k 
200k 
10 VO  0
VO  7,5V
Vi  9,375V




 0,4 Vi 3,75
VO  0,4 Vi 3,75 
VO  0,4 Vi 3, 75


I risultati ottenuti portano alla seguente transcaratteristica