Scarica

SISTEMI DI ACQUISIZIONE
E DISTRIBUZIONE DATI
SISTEMI DI ACQUISIZIONE E DISTRIBUZIONE DATI
CLASSE QUINTA A inf
Quali grandezze fisiche si possono rilevare?
•
•
•
•
•
•
•
•
•
•
Temperatura
Umidità
Pressione
Illuminazione
Rotazione angolare
Spostamento
Campo magnetico
Gas
Suono
Etc…
E’ COMPOSTO DA
• Un SOTTOSISTEMA DI MISURA a contatto con il
mondo fisico, in grado di rilevare grandezze
fisiche come temperatura, velocità, ecc;
• Un SOTTOSISTEMA DI CONTROLLO, con un’unità
centrale che fornisce i segnali di controllo e
temporizzazione per i sottosistemi di acquisizione
e di distribuzione. L’unità centrale esegue
operazioni di elaborazione e memorizzazione.
• Un SOTTOSISTEMA DI USCITA , che provvede a
generare segnali di uscita che devono comandare
motori, relè ecc..
SOTTOSISTEMA DI MISURA
E’ COMPOSTO DAI SEGUENTI BLOCCHI:
• CIRCUITO DI RILEVAZIONE
• CIRCUITO DI CONDIZIONAMENTO
• CONVERTITORE ANALOGICO/DIGITALE (o ADC)
RILEVATORE
CIRCUITO DI
CONDIZIONAMENTO
CONVERTITORE
ADC
IL CIRCUITO DI RILEVAZIONE
Trasforma la grandezza fisica da misurare in una
grandezza elettrica (tensione, corrente o
frequenza) ad essa proporzionale. Questo
compito è svolto da dispositivi noti come
TRASDUTTORI.
I TRASDUTTORI
Sono composti da due parti:
Sensore: E’ un dispositivo che rileva le variazioni di una
grandezza fisica, e modifica, proporzionalmente ad essa,
una delle sue caratteristiche elettriche (resistenza, capacità,
induttanza).
E’ un circuito elettronico che converte le
variazioni di resistenza (o capacità o di induttanza)
prodotte dal sensore, in una variazione di tensione (o
corrente, o frequenza) proporzionale ad essa.
Convertitore:
Tipi di trasduttori:
Analogico: quando il suo segnale di uscita è
una grandezza elettrica (tensione, corrente o
frequenza) che varia in modo continuo.
Digitale: quando il suo segnale di uscita è
composto da un segnale digitale, cioè un segnale
che può assumere solo due livelli di tensione
identificati come 0 e 1. Questi trasduttori si
possono interfacciare direttamente con un ADC.
I TRASDUTTORI possono essere:
Attivi: Quando forniscono in uscita un segnale
direttamente utilizzabile da circuiti di elaborazione senza
nessun consumo di energia elettrica, né richiedono
alimentazione E’ il caso delle celle fotovoltaiche e delle
termocoppie.
Passivi: Sono quei trasduttori ai quali bisogna fornire
energia elettrica perché la grandezza fisica d’uscita possa
essere trasformata in una grandezza elettrica (tensione,
corrente o frequenza). Ad esempio il Potenziometro che
fornisce in uscita valori di tensione diversi, a seconda
della posizione del cursore.
Caratteristiche fondamentali per un
trasduttore
• ELEVATA SENSIBILITA’
• USCITA LINEARE
• STABILITA’ DI FUNZIONAMENTO NEL TEMPO
Parametri caratteristici dei sensori:
a) Caratteristiche di trasferimento:
E' il legame che intercorre tra la variabile da misurare
(ingresso) e il segnale elettrico di uscita del trasduttore.
I trasduttori la cui caratteristica è una retta sono detti
lineari.
Caratteristica dei Trasduttori: la Linearita’.
U
U=KI
tg=K

I
U=KI
U: La grandezza di uscita del sensore
I: La grandezza da misurare
K: Coefficiente angolare
Quando la retta non passa per l'origine la variabile
d'uscita è diversa da zero in corrispondenza del valore
nullo della variabile di ingresso. L'equazione è:
U=KI+offset
U=Grandezza di uscita
U=KI+offset
offset
I=grandezza d' ingresso
Si definisce offset il valore non nullo della
variabile di uscita corrispondente al valore
nullo della variabile d' ingresso.
b) Linearità:
Il funzionamento ottimale di un trasduttore è quello
definito da una caratteristica lineare.
La linearita è il parametro che evidenzia la
deviazione tra la retta (caratteristica teorica) e la
curva reale.
La non linearità è il valore massimo della deviazione
rispetto alla curva teorica in valore assoluto riferito al
valore massimo del segnale di uscita.
Un sensore è buono quando la sua non linearità non
è superiore allo 0.1%.
Caratteristica ideale e reale
U=Grandezza di uscita
Caratteristica reale
Caratteristica Ideale
Deviazione
I=Grandezza d' ingresso
c) Range di funzionamento:
E' l'intervallo dei valori che può assumere la grandezza
che deve essere trasdotta.
Range di
Funzionamento
Saturazione
Zona lineare
Min
Max
d) Isteresi:
E' l' area racchiusa tra le due curve e rappresenta una
imprecisione di misura.
e) Sensibilità:
E' il rapporto tra la variazione della grandezza di uscita e
la variazione della grandezza d' ingresso che la provoca.
S=
U
I
Più il coefficiente angolare della retta è elevato più il
trasduttore è sensibile e minore sarà il range di
funzionamento.
U
Maggiore pendenzaTrasduttore più sensibile.
Valore massimo di uscita
U1
U2
l
f) Tempo di risposta:
E' il tempo che il trasduttore impiega per raggiungere
in uscita il valore di regime corrispondente al valore d'
ingresso.
g) Risoluzione:
E' il rapporto percentuale tra la minima variazione della
grandezza di uscita in grado di essere rilevata e il valore
massimo del fondo scala.
h) Ripetibilità:
E' la capacità di un sensore di fornire sempre gli stessi
valori di uscita in corrispondenza dell' ingresso.
SOTTOSISTEMA DI CONTROLLO
GENERA I SEGNALI DI CONTROLLO E TEMPORIZZAZIONE PER I
SOTTOSISTEMI DI ACQUISIZIONE E DI DISTRIBUZIONE
E’ composto da:
• Un sistema programmabile per l’elaborazione dei dati (es. un PC)
• Circuiti di d’interfaccia hardware che consentono il trasferimento
dei segnali dal sottosistema di misura all’unità di elaborazione e da
questa al sottosistema di uscita.
• Dispositivi RAM, ROM, o EEPROM per la memorizzazione dei dati e
dei programmi di acquisizione.
• Una tastiera ed un monitor (o display).
IL SOTTOSISTEMA DI CONTROLLO PUO’ ESSERE REALIZZATO
MEDIANTE:
• UN PC
• UN MICROCONTROLLORE
• UN PLC
SOTTOSISTEMA DI USCITA
GENERA I SEGNALI DI COMANDO PER GLI
ATTUATORI, I QUALI POSSONO ESSERE DI TIPO
ANALOGICO O DIGITALE.
computer
CONVERTITORE
D/A
CIRCUITO DI
CONDIZIONAMENTO
ATTUATORE
SISTEMA DI ACQUISIZIONE AD UN SOLO CANALE
E’ costituito da:
•
•
•
•
•
CIRCUITO DI RILEVAMENTO
CIRCUITO DI CONDIZIONAMENTO
CIRCUITO SAMPLE & HOLD
CONVERTITORE ADC
LOGICA DI CONTROLLO
CIRCUITO DI CONDIZIONAMENTO
Svolge le seguenti funzioni:
•
•
•
•
•
•
Conversione resistenza tensione;
Conversione corrente  tensione;
Amplificazione e traslazione di livello
Isolamento
Filtraggio
Linearizzazione.
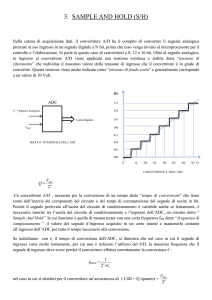
IL SAMPLE & HOLD
Il Sample & Hold è un circuito utilizzato prima del
convertitore A/D per «mantenere» (HOLD) costante
il segnale analogico all’ingresso di quest’ultimo.
Infatti un convertitore A/D ha bisogno che il segnale
analogico presente al suo ingresso si mantenga
costante per tutto il tempo di durata della
conversione.
Se così non fosse, l’A/D non riuscirebbe a convertire
correttamente a causa delle variazioni veloci del
segnale analogico al suo ingresso.
IL SAMPLE & HOLD
E’ però vero che il blocco S/H è necessario solamente se la
variazione del dato è molto veloce.
In tal caso il S&H è in grado di memorizzare il valore assunto dal
segnale in un determinato istante (fase di sample) e mantenerlo
costante all’ingresso del convertitore, per tutto il tempo
impiegato ad effettuare la conversione.
Quando la variazione del segnale è lenta, si può fare a meno del
blocco S/H e il segnale può essere applicato direttamente
all’ingresso del convertitore A/D.
Esempio di circuito S&H
Funzionamento del S&H
Quando il segnale S/H viene portato al livello alto, l’interruttore elettronico si chiude ed il
circuito è in condizione di campionamento (sample), cioè il condensatore viene caricato e
raggiunge la tensione di ingresso Vi. Lo stadio inseguitore d’ingresso permette di offrire
un‘altra impedenza all’ingresso, in modo da non caricare ed alterare la tensione Vi,
mentre contemporaneamente fornisce la corrente necessaria a caricare rapidamente il
condensatore. Quando poi il segnale S/H si porta basso, il circuito si pone nella condizione
di mantenimento (hold), in altre parole l’interruttore si apre e mantiene la tensione
raggiunta in precedenza. Lo stadio inseguitore d’uscita permette di trasferire all’uscita la
tensione ai capi del condensatore, senza scaricarlo.
IL CONVERTITORE A/D
Il convertitore A/D ha il compito di trasformare il
segnale analogico presente al suo ingresso in un
segnale digitale ad n bit.
LOGICA DI ACQUISIZIONE
II processo di conversione inizia quando tramite software (o hardware) il
convertitore riceve un segnale di inizio conversione SC (Start Conversion) dalla
logica di controllo del sistema.
Quando la conversione e terminata il convertitore genera il segnale EOC( End
Of Conversion) per indicare al sistema che il dato e disponibile. II segnale EOC
e spesso utilizzato per generare una richiesta d'interruzione e per avviare la
lettura dei dati.
AI termine della conversione sulle uscite digitali del convertitore viene posto il
valore numerico corrispondente a quello analogico presente al suo ingresso.
Per poter acquisire il dato digitale, la logica di controllo deve attivare il
segnale OE (Output Enable) che permette la lettura del dato da parte del
sistema.
Al termine del processo
il dato viene letto dalla
CPU attraverso il BUS DATI.
START CONVERSION, OUTPUT-ENABLE, END-OF-CONVERSION
• Nei convertitori direttamente interfacciabili con i sistemi a microprocessore,
i segnali che danno inizio alla conversione (SC), che ne segnalano la fine
(EOC) e che permettono la lettura del dato convertito (OE), assumono
spesso nomi diversi e, generalmente, sono collegati direttamente al bus del
microprocessore.
• IL SEGNALE START CONVERSION, SC, E’ ABILITATO QUANDO: CS = 0 , WR = 0
• IL SEGNALE OUTPUT-ENABLE, OE, E’ ABILITATO QUANDO: CS = 0 , RD = 0
• II termine della conversione e segnalato dall’ADC, che pone al livello logico
basso il pin INTR (EOC) della CPU.
LA QUANTIZZAZIONE
•
La trasformazione di un segnale analogico che può assumere infiniti valori, in un dato
digitale, implica automaticamente un’operazione di QUANTIZZAZIONE.
•
La Quantizzazione associa ad ogni tensione di ingresso compresa in un intervallo di
valori definito, uno ed un solo numero digitale.
•
i codici che possono essere rappresentati in uscita con n bit sono solo 2n
Ad esempio con 3 bit possono essere rappresentate 2 3 = 8 codici.
I codici devono quindi essere associati ad un intervallo di valori della tensione di ingresso.
•
L’operazione di quantizzazione implica ovviamente una perdita di informazione, dato
che dal codice binario di uscita non è possibile risalire al valore preciso della tensione di
ingresso, ma solo all’intervallo di valori associato a quel determinato codice. Questa
conseguenza prende il nome di «rumore di quantizzazione».
IL PASSO DI QUANTIZZAZIONE (QUANTO) e la
Tensione di Fondo Scala (o di riferimento)
Ad un convertitore viene applicata una tensione continua
particolarmente stabile detta tensione di riferimento (VREF).
Questa tensione viene anche detta tensione di fondo scala (VFS).
Si definisce QUANTO (o passo di quantizzazione), il rapporto:
Q=
𝑉𝐹𝑆
2𝑛
(Q prende il nome anche di LSB)
In alcuni convertitori ADC la risoluzione è pari a ½ LSB, invece che 1 LSB.
Esso rappresenta la risoluzione del convertitore, ovvero la più piccola
tensione che applicata all’ingresso produce un cambiamento del dato
digitale in uscita.
Nota: In alcuni testi, la risoluzione viene definita in altro modo, e coincide con il
numero di bit, n, del dato di uscita.
I più comuni convertitori presenti sui mercato hanno un numero di bit n pari a 8,
12, 16 bit (sono comunque reperibili anche con risoluzioni di 10, 14, 18,20 bit).
ESEMPIO
All’ingresso di un convertitore A/D con numero di
bit n=8, si applichi una tensione analogica
Vi=3,2 [V].
Sapendo che VFS=5,12 [V], quanto vale il numero
generato N dalla conversione A/D ?
Soluzione:
Facendo un proporzione, si ottiene:
VFS : Vi = 2n : N
256
Da cui, sostituendo i dati: N = 3,2 ∙ 5,12
=160
Che trasformato in binario è 1010 0000
RUMORE DI QUANTIZZAZIONE
• L’operazione di conversione A/D associa ad un intervallo di valori
della tensione in ingresso un unico codice binario. Per eseguire
l’operazione inversa, a ciascun codice si associa un valore di
tensione che è il valore centrale di ciascun intervallo,
chiamato valore nominale del codice. L’operazione di
quantizzazione fa quindi perdere informazione: solo nel caso in cui
la tensione Vi è esattamente uguale ad uno dei valori nominali
associati ai codici, l’operazione può considerarsi trasparente,
mentre in tutti gli altri casi si avrà un errore.
• L’ampiezza massima dell’errore commesso è pari a metà
dell’intervallo di tensione , cioè:
E = ½ * Q = VFS/2^(n+1)
• L’effetto di tale errore può essere considerato come un rumore
aggiunto alla tensione di ingresso.
• Complessivamente l’operazione di quantizzazione degrada il
segnale di ingresso, peggiorando il rapporto segnale/rumore (S/N).
ADC FLASH
I convertitori A/D sono disponibili
in una grande varietà di tipi che si
differenziano per numerosi fattori.
Un convertitore che effettua molto
velocemente la conversione A/D è
quello denominato FLASH.
Il tempo tipico di conversione è
dell’ordine di 10 ns.
Di
seguito
mostriamo
un
convertitore FLASH con uscita a 3
bit costituito da sette comparatori,
da un registro a latch per la
sincronizzazione della conversione
e da un codificatore.
• l segnale Va da convertire viene applicato agli ingressi non
invertenti; l’ingresso invertente di un comparatore è connesso ad
una rete resistiva che ripartisce la tensione di riferimento Vref in
otto fasce, così da fissare i livelli di riferimento, o di
quantizzazione, ai valori 1/14 Vref, 3/14 Vref, …., 13/14 Vref.
• Ciascun comparatore commuta la sua uscita ad 1 quando Va
supera il rispettivo livello di riferimento. Le uscite dei comparatori
vengono memorizzate in sincronismo con il segnale di clock e
codificate per fornire un dato digitale binario.
• Il convertitore è in grado di convertire segnali analogici con
escursione da 0 a Vref con un errore di quantizzazione costante e
sempre minore di ± ½ LSB. Supponendo Vref = 7 V, si ottengono i
livelli di riferimento rappresentati di seguito:
Funzionamento del circuito:
• Per tutti i valori di Va inferiore a 1/14 Vref = 0.5 V tutti i comparatori hanno
l’uscita bassa e quindi il codice di uscita è 000.
• Per tutti i valori di Va compresi fra 0.5 V e 3/14 Vref =1.5 V, solo l’uscita di C1
si porta al livello alto e l’uscita digitale indica 001.
• E così via per gli altri valori di Va.
Specifiche dei convertitori A/D
• Risoluzione
• Tempo di conversione
• Gli errori di linearità, guadagno, offset
TEMPO DI CONVERSIONE Tc
• Quando si applica una tensione Vi all’ingresso di un ADC, è
necessario attendere un certo tempo prima che il corrispondente
codice sia disponibile in uscita. Tale tempo è chiamato tempo di
conversione (Tc).
• Il valore di Tc pone due limiti fondamentali all’utilizzo di un ADC:
- Il primo riguarda, come già detto in precedenza, la velocità di
variazione del segnale di ingresso, che non deve variare
apprezzabilmente durante il tempo di conversione.
- Il secondo limite riguarda la frequenza di lettura dei dati di
uscita del convertitore. Ad esempio, avendo un ADC con un
tempo di conversione di 1ms, non è possibile chiedere al
convertitore i dati in uscita con una frequenza superiore a
quella di un dato ogni microsecondo.
Errore di linearità
L'errore di linearità rappresenta il massimo scostamento
della caratteristica reale da quella ideale
Errore di guadagno
Graficamente è una variazione della pendenza della retta interpolante
rispetto a quella ideale.
L'alterazione è dovuta a una imprecisione del valore di riferimento della
tensione e a imperfette amplificazioni o attenuazioni negli stadi del
dispositivo ADC che precedono il convertitore vero e proprio.
La conseguenza è l'introduzione di un errore di tipo lineare, chiamato errore
di guadagno.
Errore di offset
Graficamente l'errore di offset è una traslazione della curva
caratteristica a gradinata (e, conseguentemente anche della retta
interpolante) parallelamente a se stessa, verso destra o verso
sinistra, mantenendo inalterate le ampiezze dei tratti orizzontali e dei
tratti verticali.
Per effetto dell'errore di offset un ADC può fornire un codice di uscita
diverso da zero in corrispondenza di un valore nullo della tensione
analogica di ingresso (cioè in corrispondenza di Vi=0), cosa che nel
convertitore ideale non accade.
Massima frequenza del segnale che è
possibile convertire con solo un ADC
Si può dimostrare (ma omettiamo la dimostrazione per semplicità)
che il valore massimo della frequenza del segnale che è
possibile convertire con solo un ADC è:
• 𝑓𝑚𝑎𝑥 ≤
1
2𝑛:1 ∙𝜋∙𝑡𝑐
(per ADC con risoluzione di ½
• 𝑓𝑚𝑎𝑥 ≤
1
2𝑛 ∙𝜋∙𝑡𝑐
(per ADC con risoluzione di 1 LSB)
LSB)
Come si deduce dalle formule, fMAX, dipende solo dal numero di
bit n e dal tempo di conversione tc.
Esempi:
Esempio 1:
Un convertitore ad 8 bit con tempo di conversione pari a
100 µs, può convertire con un errore di ½ LSB, segnali
aventi una frequenza massima uguale a:
1
1
𝑓𝑚𝑎𝑥 ≤ 2𝑛:1∙𝜋∙𝑡 = 8:1
= 6,2 Hz
2
∙3,14∙100∙10;6
𝑐
Esempio 2:
Un convertitore a 12 bit, con un tempo di conversione pari
a 35 µs, può convertire con un errore di ½ LSB, segnali
aventi una frequenza massima uguale a:
𝑓𝑚𝑎𝑥 ≤
1
2𝑛:1 ∙𝜋∙𝑡𝑐
1
= 12:1
2
∙3,14∙35∙10;6
= 1,1 Hz
Specifiche del Sample & Hold
In un circuito S&H reale la carica del condensatore non è istantanea, così come la corrente
di scarica in condizioni di hold non è nulla. Pertanto un circuito reale risulta caratterizzato
da due parametri fondamentali:
TEMPO DI APERTURA (Ta)
E’ l’intervallo di tempo richiesto all’interruttore interno per aprirsi completamente, dopo
che è stato dato il comando di Hold. L’ordine di grandezza è qualche centinaia di ns.
TEMPO DI ACQUISIZIONE (Tac)
Tac rappresenta il tempo di carica del condensatore in condizioni di campionamento. I valori
più comuni sono dell’ordine dei µs, ma sono disponibili circuiti S&H integrati con Tac
dell’ordine dei ns. Affinché un circuito S&H risulti utile, deve avere un tempo d’acquisizione
inferiore al tempo Tc del convertitore A/D per cui è stato scelto.
VELOCITA’ DI SCARICA
La velocità di scarica esprime, in mV al secondo, la perdita di tensione sul condensatore in
condizioni di mantenimento. Anche tale valore deve essere scelto in modo che, durante il
tempo di conversione Tc, non si ripresenti il problema dell’errore di conversione.
Massima frequenza del segnale che è
possibile convertire con ADC + S/H
Anche in questo caso si può dimostrare (ma omettiamo la
dimostrazione) che il valore massimo della frequenza del
segnale che è possibile convertire con l’insieme di un
ADC + un Sample & Hold è:
• 𝑓𝑚𝑎𝑥 ≤
• 𝑓𝑚𝑎𝑥 ≤
1
2𝑛:1 ∙𝜋∙𝑡𝑎
1
2𝑛 ∙𝜋∙𝑡𝑎
(per ADC con risoluzione di ½
LSB)
(per ADC con risoluzione di 1 LSB)
Si può osservare come il valore della max frequenza del segnale
aumenta in questo caso, perché il tempo di apertura ta del S/H è
molto più piccolo del tempo di conversione tc dell’ADC.
Esempio:
Si scelga un Sample & Hold con tempo di apertura
uguale a 20 ns, facendo riferimento ad un
convertitore A/D ad 8 bit. La frequenza massima
del segnale ammesso in ingresso è uguale a:
1
1
𝑓𝑚𝑎𝑥 ≤ 𝑛:1
= 28:1∙3,14∙20∙10;9 = 𝟑𝟏 KHz
2
∙𝜋∙𝑡𝑎
Come si può notare, in questo caso la massima
frequenza del segnale di ingresso è
notevolmente più alta che nel caso in cui si
considera l’ADC da solo senza S&H.
Convertitori A/D con track-hold interno
Alcuni convertitori A/D hanno incorporato al loro interno
un particolare Sample & Hold denominato Track-Hold.
• Un Sample & Hold normale campiona il segnale (fase di
sample) per la maggior parte del tempo, mentre va nella
fase di Hold per il breve periodo della conversione.
• Il Track-Hold, invece, viene usato per la maggior parte
del tempo nella fase di track (ovvero segue l’andamento
del segnale di ingresso) e solo per un breve periodo è
portato nella fase di mantenimento.
Teorema di Shannon
La frequenza con cui si leggono i dati in uscita è
detta frequenza di campionamento (fc).
Il valore massimo di fc è stabilito dal teorema del
campionamento di Shannon che stabilisce che la frequenza di
campionamento Fc deve essere almeno doppia della massima
frequenza del segnale da convertire Fmax.
𝑭𝒄 ≥ 𝟐 ∙ 𝑭𝒎𝒂𝒙
Se non viene rispettata tale condizione, il segnale campionato non
determina in maniera fedele il segnale analogico.
In realtà conviene effettuare il campionamento, se possibile, a
frequenza superiori, almeno a 5 ∙ 𝑭𝒎𝒂𝒙
CAMPIONAMENTO CON ADC + S/H
Quanto tempo occorre aspettare fra una operazione di conversione A/D ed
un’altra?
In effetti occorre aspettare che l’ADC abbia terminato la conversione
precedente e che il Sample & Hold fornisca un segnale stabile all’uscita.
Si deve cioè attendere un periodo di tempo T pari alla somma dei tempi:
T = Tac + Ta + Tc
Poiché la frequenza è l’inverso del periodo T, allora la frequenza con la quale
si può campionare il segnale è pari a:
𝑓
1
𝐶𝑚𝑎𝑥 ≤
(𝑇𝑎𝑐+𝑇𝑎+𝑇𝑐)
E, in accordo con il teorema di Shannon, il segnale di ingresso, per poter
essere campionato correttamente con il S/H, deve avere un valore massimo
della frequenza pari a:
𝒇
𝒇𝒄𝒎𝒂𝒙
𝟏
𝐦𝐚𝐱 ≤
𝟐
=
𝟐∙(𝑻𝒂𝒄 +𝑻𝒂 +𝑻𝒄 )
ARCHITETTURA DI UN SISTEMA
DI ACQUISIZIONE MULTICANALE
Architettura di un sistema di acquisizione
multicanale
Quando è necessario rilevare più grandezze in ingresso, il sistema di
acquisizione diviene più complesso, composto da catene di acquisizione
in parallelo e dipendenti una dalle altre almeno fino al filtro P.B.
Le frequenze di campionamento in questo modo non sono molto
elevate.
Questa soluzione prevede un unico circuito S/H ed un solo convertitore
A/D, la selezione del canale è resa possibile da un multiplexer analogico
(MUX), schematizzato con un commutatore elettronico a più ingressi ed
una sola uscita.
Un mux analogico è costituito da un certo numero di interruttori
elettronici, realizzati o in tecnologia JFET o CMOS o MOSFET.
Quale degli ingressi viene selezionato a passare in uscita? Dipende dai bit
S0…Sn la cui combinazione specifica quale ingresso viene selezionato.
APPENDICE:
1. DAC a resistori pesati
2. ADC ad approssimazioni
successive
DAC a resistori pesati
DAC a resistori pesati
DAC a resistori pesati
DAC a resistori pesati
DAC a resistori pesati
Vantaggi e svantaggi
• Vantaggi della configurazione:
 Semplicità;
 Ridotto numero di resistori (n resistori per un codice di n bit).
• Svantaggio della configurazione:
 L’ accuratezza del DAC dipende dalla stabilità di Vref, dai valori
delle resistenze e dalla qualità degli interruttori.
 Valori molto diversi di resistenza da integrare su singolo chip
 difficoltà di realizzare il preciso rapporto dei resistori
(occorre una bassissima tolleranza del valore delle
resistenze);
 La corrente assorbita dal circuito dipende dalla
configurazione dei bit di ingresso;
ADC AD APPROSSIMAZIONI SUCCESSIVE
Nell'ADC ad approssimazioni successive (in inglese: successive approximation ADC) la
logica di controllo è costituita da un registro ad approssimazioni successive (S.A.R. =
Successive Approximation Register):
ADC AD APPROSSIMAZIONI SUCCESSIVE
Come negli ADC a conteggio, anche in questo caso la conversione avviene
confrontando l'uscita di un convertitore DA con la tensione analogica da
convertire. Il funzionamento è il seguente:
L'inizio della conversione viene attivato inviando al S.A.R. il segnale SOC. In
questo modo nel SAR viene caricata una parola nella quale il solo bit più
significativo (MSB) è posto a 1 (tutti gli altri bit sono a zero). L'uscita del
DAC, pertanto, assume il valore corrispondente al suddetto codice.
Se Vin > VD il S.A.R. mantiene MSB a 1 e carica un altro 1 nel bit
immediatamente successivo (cioè pone un 1 anche nel bit n-1).
Se, invece Vin > VD il S.A.R. pone MSB a 0 e carica un 1 nel bit
immediatamente successivo (cioè nel bit n-1).
I passi precedenti vengono ripetuti allo stesso modo per i bit successivi.
ADC AD APPROSSIMAZIONI SUCCESSIVE
Facciamo un esempio:
Consideriamo un convertitore a 4 bit.
All'inizio il S.A.R. viene inizializzato col codice 1000 (MSB a 1 e tutti
gli altri bit a zero). Tale codice viene convertito in una tensione
analogica dal DAC e confrontato con la Vin. Se Vin è maggiore di
tale tensione, viene generato il nuovo codice 1100 (cioè viene
messo a 1 anche il bit immediatamente successivo all'MSB). Se
invece Vin è minore, il nuovo codice generato sarà 0100 (viene
azzerato l'MSB e posto a 1 il bit immediatamente successivo).
L'algoritmo di conversione procede allo stesso modo per i bit
successivi, come mostrato in figura:
ADC AD APPROSSIMAZIONI SUCCESSIVE
ADC AD APPROSSIMAZIONI SUCCESSIVE
Il tempo di conversione dell’ADC ad approssimazioni successive è costante
qualunque sia il valore del campione bit Vin. Indicando con TCK il periodo del
CLOCK e con n bit il numero di Bit del convertitore, il tempo di conversione Tconv
è:
Tconv = n * TCK
Il tempo di conversione non dipende dal valore del campione Vin. Al crescere
della risoluzione dell'ADC il tempo di conversione aumenta. Tale incremento,
però, può essere compensato dalla diminuzione di TCK, cioè dall'aumento della
frequenza del CLOCK. Ciò consente di ottenere tempi di conversione costanti e
ragionevolmente contenuti. Per queste ragioni gli ADC ad approssimazioni
successive costituiscono una delle soluzioni circuitali più adottate dai costruttori e
impiegate in svariati settori applicativi.
DAC integrati (1/3)
• Tutti i DAC integrati hanno al loro
interno i due blocchi della
struttura corrispondenti a set di
interruttori (elettronici) e rete
resistiva.
• Alcuni di essi generano al loro
interno la Vref a partire dalla Vcc;
• Altri presentano un piedino sul
quale la Vref deve essere resa
disponibile dall’esterno (generata
da appositi riferimenti di
tensione, che consentono una
maggior stabilità della tensione di
riferimento, nel tempo e con la
temperatura).
DAC integrati (2/3)
• La maggior parte dei DAC
integrati ha una uscita in
corrente; alcuni integrano
anche il convertitore I/V
fornendo l’uscita in
tensione.
• Alcuni DAC accettano in
ingresso il dato digitale
(generalmente in binario
puro) sotto forma parallela,
altri sotto forma seriale per
poter ridurre il numero di
piedini del componente.
DAC integrati (3/3)
• Alcuni DAC dispongono di un
buffer-latch di ingresso che
consente l’interfacciamento
diretto con la CPU.
• Questa, infatti, una volta
indirizzato il DAC (visto come
una periferica di uscita) e
caricato il dato nel bufferlatch, può continuare ad
eseguire il suo programma e
limitarsi ad aggiornare il
dato, se necessario.
Interfacciamento DACμP (1/4)
• Vi sono diverse modalità di interfacciamento tra μP e DAC, a seconda del
tipo di CPU e di DAC integrato che si usa.
• I fogli tecnici allegati ai DAC (come del resto agli ADC) presentano, oltre alle
caratteristiche elettriche, diversi schemi applicativi di interfacciamento e
misura, che evidenziano aspetti particolari relativi alle tensioni di riferimento
e a speciali connessioni di uscita.
Interfacciamento DACμP (2/4)
• 1° esempio: il convertitore digitale analogico della figura precedente è il
DAC0830 che presenta uscita in corrente.
• L’operazionale U1 si comporta da convertitore corrente-tensione e
l’operazionale U2 è in configurazione invertente a guadagno unitario.
• In tal caso la tensione di uscita Vo che si ottiene è compresa tra 0 e 5V
secondo la formula: Vo= (VFS/2n)N = (VREF/28)N = (5/256)N.
Interfacciamento DACμP (3/4)
• 2° esempio: schema di interfacciamento tra un DAC a 8
bit (dotato di segnali di controllo Chip Select e WRite) e
un microprocessore a 8 bit (ad es. lo Z80).
Interfacciamento DACμP (4/4)
• Quando la CPU attiva il segnale IORQ , la Logica di controllo decodifica
l’indirizzo del DAC (presente sul bus indirizzi della CPU) e, tramite il segnale CS
, abilita il funzionamento del DAC. Il DAC, da parte sua, grazie al segnale di WR
, riconosce automaticamente le operazioni di lettura e scrittura:
 quando entrambe sono a livello basso, i bit d’ingresso vengono convertiti;
 quando almeno una delle due linee è a livello alto il convertitore mantiene
l’uscita precedente.