Azione diaframma in strutture prefabbricate con pannelli di
parete
Fabio Biondini, Bruno Dal Lago, Giandomenico Toniolo
Dipartimento di Ingegneria Civile e Ambientale, Politecnico di Milano, Piazza Leonardo da Vinci 32, 20133 Milano
Keywords: diaphragm action, precast structures, cladding panels, seismic behaviour.
ABSTRACT
Past seismic events, including L’Aquila earthquake in 2009 and Emilia earthquake in 2012, clearly
demonstrated the inadequacy of the current design approach for the connection system of the cladding
wall panels of precast buildings. To clarify this problem, the present paper investigates the seismic
behaviour of a traditional precast structural frame system for industrial buildings with different type of
connections of its cladding wall panels. The wall cladding system consists of a statically determined
pendulum arrangement of panels, each supported with two hinges to the structure, one at the top and one
at the bottom, so to have under seismic action a pure frame behaviour where the wall panels are masses
without stiffness. Adding mutual connections between the panels, the wall cladding system becomes part
of the resisting structure, leading to a dual frame/wall system or to a wall system depending on the
stiffness of the connections. Also diaphragm connections are considered, ranging from roof elements
single hinge connections on their ends, without diaphragm action, to an imposed rigid diaphragm. The
results of a parametric investigation based on linear and non-linear dynamic analyses show how the main
characteristics of the structural behaviour play their role within the structural assembly for different
degrees of interaction between frames, panels and diaphragm. The results of non-linear dynamic analyses
under a recorded modified accelerogram show the seismic performance of the dual frame/wall system
with dissipative connections between panels and the effectiveness of the diaphragm action of the roof
system.
1
INTRODUZIONE
Le strutture prefabbricate a telaio ad uso
industriale o commerciale hanno spesso coperture
che sono composte da elementi di solaio
distanziati con lucernai interposti. Con tale
soluzione l’azione diaframma può essere nulla o
parziale a seconda delle connessioni terminali
degli elementi di solaio con le travi e della loro
rigidezza nel piano del diaframma. Per avere un
diaframma rigido sono necessari elementi di
solaio a contatto tra loro e con adeguate
reciproche connessioni.
Le azioni sull’impalcato derivanti da carichi
orizzontali di tipo sismico impegnano il
diaframma di piano sulla base della distribuzione
di masse e rigidezze tra i diversi telai affiancati.
Il problema del comportamento a diaframma
degli impalcati prefabbricati è stato studiato in
letteratura da Fleischman et al. (2001) e da
Ferrara et al. (2004) con riferimento a schemi
tipici della prefabbricazione europea.
In totale assenza di un diaframma rigido di
piano, ciascun telaio dell’assieme strutturale si
comporta in modo sostanzialmente indipendente
rispetto agli altri, sulla base delle proprie
caratteristiche di rigidezza e delle masse che gli
competono.
Un sistema strutturale con omogenea
distribuzione di masse e rigidezze si comporta
pertanto in modo più uniforme, impegnando
lievemente l’eventuale diaframma rigido, mentre
la presenza di sproporzioni di masse e/o rigidezze
altera la risposta strutturale e provoca risposte
fuori fase dei diversi telai, con conseguente
distorsione dell’impalcato. Maggiore è la
sproporzione, maggiori sono le forze che
impegnano l’eventuale diaframma e le sue
connessioni.
Tale problema è esaltato in presenza di sistemi
iperstatici di connessione dei pannelli di
tamponamento alla struttura, come descritto in
Biondini et al. (2013), dove i pannelli perimetrali
si comportano come pareti di grande rigidezza.
Nel presente lavoro si studia il comportamento
sismico di un tipico edificio prefabbricato
mediante analisi dinamiche modali e non-lineari.
Si intende mostrare quale è il comportamento
dell’edificio soggetto a forze orizzontali al variare
delle proprietà delle connessioni di diaframma e
delle connessioni dei pannelli di tamponamento
perimetrali, studiando configurazioni con
crescente differenza tra la rigidezza del telaio
centrale e quella delle pareti esterne.
2
posizionati esclusivamente in direzione parallela
alle travi.
In Figura 1b è riportato il dettaglio delle
connessioni, a cerniera quelle inferiori e superiori
tra il pannello di parete e le travi di fondazione e
di copertura, a scorrimento deformabili quelle
reciproche tra i pannelli. Le connessioni tra
tegolo e trave sono differenti per le due nervature:
una è a cerniera, l’altra a scorrimento
deformabile.
(a)
PROTOTIPO DI CALCOLO
L’influenza sul comportamento strutturale di
differenti connessioni tra pannello e pannello e tra
solaio e trave viene studiata attraverso un
modello tridimensionale di un tipico telaio
prefabbricato monopiano di 2 navate di luce 15 m
e 4 campate ciascuna lunga 10 m. La struttura
mostrata in Figura 1a è composta da pilastri di
altezza 7 m e sezione 0,6 x 0,6 m. Le travi hanno
sezione rettangolare di 0,8 x 0,4 m e coprono le
luci di 10 m, mentre i tegoli hanno sezione a TT
di altezza 0,6 m, larghezza 2,1 m e coprono le
luci maggiori di 15 m. I tegoli sono disposti
distanziati per lasciare spazio ai lucernai. La
massa distribuita dei tegoli e dei carichi
permanenti è di 285 kg/m2.
I pannelli di tamponamento hanno dimensioni
di 2,5 x 8,75 m, spessore equivalente di 12 cm e
massa distribuita di 300 kg/m2. I pannelli sono
(b)
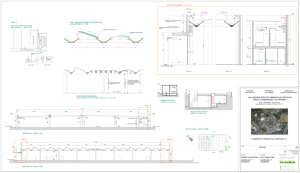
Figura 1. Prototipo di edificio prefabbricato: a) pianta e
prospetto; b) particolare del prospetto e connessioni oggetto
di studio.
ANALISI MODALE
Frequenza [Hz]
20
15
10
5
0
1E+00
1E+02
1E+04
1E+06
1E+08
Rigidezza connessione pannello-­‐pannello kp [kN/m]
1E+10
(a)
100
Fattore di partecipazione [%]
90
80
70
60
50
40
30
20
10
0
1E+00
1E+02
1E+04
1E+06
1E+08
Rigidezza connessione pannello-­‐pannello kp [kN/m]
1E+10
(b)
Figura 2. Edificio con piano rigido con differente rigidezza
kp delle connessioni pannello-pannello; a) frequenze, b)
fattori di partecipazione.
6
kp = 1010 kN/m
5
Frequenza del 1° modo [Hz]
L’analisi
dinamica
modale
è
condotta
considerando la rigidezza dei pilastri dimezzata
rispetto al valore effettivo, come suggerito
dall’Eurocodice
8
per
tenere
conto
forfettariamente della fessurazione delle loro
sezioni, e assumendo la rigidezza piena per gli
altri elementi.
Si illustrano in Figura 2a e 2b i risultati relativi
all’analisi modale dell’edificio al variare della
rigidezza kp delle connessioni pannello-pannello
nel caso di diaframma rigido.
La condizione di rigidezza nulla delle
connessioni corrisponde al comportamento a
telaio della struttura e porta a una certa
flessibilità, con frequenza naturale di 0,97 Hz. La
condizione di massima rigidezza delle
connessioni tra pannello e pannello (1010 kN/m)
fa riferimento invece ad un comportamento a
parete dei pannelli di tamponamento, dando
luogo a una risposta estremamente rigida, con
frequenza naturale associata al primo modo di
vibrare di 19,78 Hz.
Per valori crescenti della rigidezza delle
connessioni tra pannelli, si verifica un
irrigidimento complessivo della struttura. In
particolare, l’intervallo di rigidezza delle
connessioni tra 104 e 106 kN/m rappresenta la
fase di transizione dal comportamento a telaio a
quello a parete.
La somma dei fattori di partecipazione
associati ai modi fondamentali di vibrare è
invariante
rispetto
alla
rigidezza
delle
connessioni. La sua entità è di circa l’87% della
massa complessiva e la restante porzione
corrisponde a numerosi modi di vibrare locali di
pannelli e pilastri, cui è associata per ciascuno
una quota molto ridotta di massa partecipante.
Andando a rimuovere l’ipotesi semplificativa
di piano rigido, resta l’effetto dei tegoli TT
vincolati come sono alle travi attraverso
connessioni su entrambe le nervature. Per
analizzare l’influenza di un’azione diaframma
parziale, con diversi gradi di rigidezza, le
connessioni sono modellate come cerniere su una
nervatura, sull’altra nervatura come deformabili,
riproducendo in questo modo una rigidezza
rotatoria attorno alla verticale del vincolo
terminale del tegolo. Si è quindi studiato il
comportamento dinamico dell’edificio con diversi
gradi di rigidezza del diaframma di piano.
25
106 kN/m
105 kN/m
4
3
104 kN/m
2
102 kN/m
1
0
1E+00
kp = 0 1E+02
1E+04
1E+06
1E+08
Rigidezza connessione tegolo-­‐trave kt [kN/m]
1E+10
(a)
100
Fattore di partecipazione 1° modo [%]
3
90
80
70
kp = 0 102 kN/m
104 kN/m
60
50
105 kN/m
40
106 kN/m
30
kp = 1010 kN/m
20
10
0
1E+00
1E+02
1E+04
1E+06
1E+08
Rigidezza connessione tegolo-­‐trave kt [kN/m]
1E+10
(b)
Figura 3. Edificio con differente rigidezza delle connessioni
tegolo-trave kt e pannello-pannello kp; a) frequenze, b)
fattori di partecipazione.
Nelle figure 3a e 3b sono riportati
rispettivamente le frequenze e i fattori di
partecipazione del primo modo di vibrare al
variare della rigidezza a taglio kt della
connessione deformabile tra tegolo e trave. La
rigidezza nulla di tale connessione corrisponde a
un vincolo su una singola nervatura del tegolo TT
(oppure alla connessione di un elemento mononervato), mentre la massima rigidezza (kt = 1010
kN/m) corrisponde a un incastro perfetto dei
tegoli nel piano dell’impalcato.
Per kt = 0 il primo modo di vibrare ha
frequenza e fattore di partecipazione uguali per
tutti i valori di rigidezza kp delle connessioni tra
pannelli. Questo poiché, con tegoli vincolati
come bielle, il primo corrisponde alla vibrazione
del telaio centrale isolato con frequenza pari a
0,91 Hz.
Nel caso di edifici con connessioni tra pannelli
poco rigide si ha un comportamento dinamico
simile al crescere della rigidezza del diaframma,
in quanto le frequenze proprie di vibrazione dei
diversi telai isolati risultano molto prossime.
Inoltre, all’aumentare dell’effetto diaframma, la
frequenza del primo modo di vibrare si riporta al
valore di 0,97 Hz, corrispondente all’ipotesi di
diaframma rigido.
Per valori crescenti di rigidezza kp delle
connessioni dei pannelli, si riscontra che
all’aumentare dell’effetto diaframma corrisponde
un graduale irrigidimento del primo modo di
vibrare, con il telaio centrale sempre più
vincolato ai telai esterni. E’ interessante notare
come il valore di soglia che si raggiunge per
connessioni rigide, pari a 5,61 Hz, risulti
notevolmente inferiore a quello di 18,91 Hz
raggiunto considerando il piano rigido. Ciò è
dovuto alla deformabilità propria dei tegoli e
suggerisce che, al crescere del divario di
comportamento dinamico dei diversi telai
componenti l’edificio, l’orizzontamento non
possa essere considerato perfettamente rigido
anche in presenza di vincoli di incastro perfetti.
Dalle considerazioni appena svolte si evince
che, al crescere della disuguaglianza dei modi di
vibrare dei diversi telai considerati singolarmente,
cresce l’impegno del diaframma, sia nelle sue
connessioni, sia negli elementi che lo
compongono.
E’ possibile anche individuare le tendenze dei
differenti comportamenti: la frequenza propria del
primo modo di vibrare subisce una forte
variazione per valori di rigidezza kp intermedi, tra
104 e 107 kN/m, e si assesta su differenti livelli di
frequenza per elevate rigidezze kt, crescenti con
la rigidezza kp.
Il fattore di partecipazione presenta invece una
zona di transizione fortemente dipendente dalla
rigidezza kp delle connessioni tra pannelli, in
particolare da 102 a 104 kN/m per valori bassi di
kp e da 105 a 107 kN/m per valori elevati di kp, e
si assesta su valori decrescenti all’aumentare
della rigidezza kp. Per quanto riguarda i modi
superiori di vibrare, nella tabelle 1 e 2 sono
riportati alcuni dei risultati più significativi delle
analisi modali, suddivisi per comportamento nel
piano e fuori piano dei pannelli. Frequenze
multiple indicano che il comportamento dinamico
è individuato da modi differenti per i diversi telai.
In questi casi viene indicato l’intervallo di
frequenze che coinvolgono la corrispondente
somma dei fattori di partecipazione.
Nel piano dei pannelli si individuano 3
comportamenti dinamici principali:
- Modo 1: deformazione complessiva del
telaio con spostamento in sommità
- Modo 2: flessione locale del telaio senza
spostamento in sommità
- Modo 3: flessione locale dei pannelli con
spostamento in sommità
Si nota come, per l’edificio con pannelli
isostatici, al passare dalla condizione di assenza
di piano rigido (kt = 0) a quella di tegoli
perfettamente incastrati (kt = 1010 kN/m), non vi
siano cambiamenti apprezzabili nel primo e unico
modo di vibrare significativo. Per l’edificio con
pannelli tra loro connessi rigidamente il
comportamento
dinamico
si
modifica
sostanzialmente solo nei riguardi del primo modo
di vibrare, mentre i modi superiori mantengono
valori di frequenza e massa partecipante simili
(Tabella 1).
Fuori dal piano dei pannelli si individuano
invece 4 comportamenti dinamici principali:
- Modo 1: flessione coordinata di tutti i telai
con spostamento in sommità
- Modo 2: flessione in controfase dei telai
esterni e centrali con spostamento in
sommità
- Modo 3: flessione dei pannelli con singola
curvatura
- Modo 4: flessione dei pannelli con doppia
curvatura
Si nota come, al passare dalla condizione di
assenza di piano rigido (kt = 0) a quella di tegoli
perfettamente incastrati (kt = 1010 kN/m), non vi
siano cambiamenti significativi nei modi di
vibrare né per l’edificio con pannelli isostatici, né
per l’edificio con pannelli connessi rigidamente
tra di loro, fatta eccezione per il modo 2, con
vibrazione in controfase dei telai, che si attiva
solo per bassi valori della rigidezza a taglio kt
delle connessioni dei tegoli (Tabella 2).
Direzione parallela ai pannelli -­‐ k p = 0
MODO
1
2
3
0,91 -­‐ 1,00
-­‐
-­‐
kt = 0
86,45
-­‐
-­‐
0,97
-­‐
-­‐
10
kt = 10
86,35
-­‐
-­‐
Frequenza [Hz]
Fattore di part. [%]
Frequenza [Hz]
Fattore di part. [%]
Riguardo alle connessioni tegolo - trave, si
considerano le seguenti tipologie:
-
diaframma rigido
-
connessione rigida (nervature entrambe
connesse rigidamente alla trave)
-
connessione a cerniera (solo una nervatura
connessa rigidamente alla trave)
(a)
Direzione parallela ai pannelli -­‐ k p = 1010
MODO
kt = 0
kt = 1010
1
0,91
29,64
5,61
32,54
2
3
19,76 -­‐ 20,25 26,91 -­‐ 27,01
15,90
41,61
19,78 -­‐ 20,27 27,46 -­‐ 27,52
13,59
41,50
Frequenza [Hz]
Fattore di part. [%]
Frequenza [Hz]
Fattore di part. [%]
(b)
Tabella 1. Frequenze e fattori di partecipazione per i modi
di vibrare significativi in direzione parallela ai pannelli; a)
kp = 0, b) kp = 1010 kN/m.
MODO
kt = 0
kt = 1010
Direzione ortogonale ai pannelli -­‐ kp = 0
1
2
3
0,91 -­‐ 1,00
1,56
5,40 -­‐ 5,42
80,99
1,81
5,93
0,96
-­‐
5,41 -­‐ 5,45
83,15
-­‐
5,62
(a)
4
-­‐
-­‐
-­‐
-­‐
Frequenza [Hz]
Fattore di part. [%]
Frequenza [Hz]
Fattore di part. [%]
4
20,06
1,08
19,38
2,14
Frequenza [Hz]
Fattore di part. [%]
Frequenza [Hz]
Fattore di part. [%]
(a)
Direzione ortogonale ai pannelli -­‐ kp = 1010
1
2
3
0,92
1,57
5,46 -­‐ 5,49
kt = 0
81,08
1,75
7,01
0,96
-­‐
5,47 -­‐ 5,50
kt = 1010
83,17
-­‐
7,33
MODO
(b)
Tabella 2. Frequenze e fattori di partecipazione per i modi
di vibrare significativi in direzione ortogonale ai pannelli;
a) kp = 0, b) kp = 1010 kN/m.
4
ANALISI DINAMICA NON LINEARE
Il comportamento della struttura sottoposta ad
azione sismica viene studiato mediante analisi
dinamica non lineare.
Per
l’azione
sismica
si
considera
l’accelerogramma registrato a Tolmezzo (1971)
scalato a PGA = 0,32g e arricchito in frequenze in
modo da renderlo compatibile con lo spettro di
risposta elastico dell’Eurocodice 8 per suolo tipo
B (Figura 4). L’analisi è stata viene ripetuta per
diverse combinazioni di connessioni tra pannelli e
per differenti deformabilità del solaio. Riguardo
alle connessioni tra pannello e pannello, vengono
esaminate le seguenti soluzioni:
-
connessioni assenti
-
connessioni rigide
-
connessioni dissipative (ad attrito)
(b)
Figura 4. (a) Accelerogramma di Tolmezzo arricchito in
frequenze; b) spettro di risposta a confronto con il modello
dell’Eurocodice 8.
4.1
Assetto isostatico
La Figura 5 mostra le curve vibratorie riferite agli
spostamenti in sommità dei telai centrale ed
esterni della struttura con assetto isostatico dei
pannelli per le 3 differenti tipologie di
diaframma.
Nel caso di tegoli incastrati alle travi non vi è
differenza tra gli spostamenti dei diversi telai,
come nel caso di diaframma rigido.
L’edificio mostra un comportamento flessibile,
con il raggiungimento di uno spostamento
massimo pari a circa 18 cm.
Considerando invece un vincolo a cerniera tra
tegoli e travi, che corrisponde a un diaframma
infinitamente flessibile, si ha un lieve sfasamento
tra le risposte del telaio centrale e dei telai esterni
dovuto alla differenza delle rispettive masse
vibranti.
200
Telaio centrale
Telaio esterno
150
Spostamento [mm]
100
50
0
-­‐50
-­‐100
-­‐150
-­‐200
0
2
4
6
8
10
12
Tempo [s]
14
16
18
20
(a)
200
Telaio centrale
Telaio esterno
150
Spostamento [mm]
100
50
0
-­‐50
Con ipotesi di tegoli connessi rigidamente alle
travi, si ottengono curve vibratorie notevolmente
differenti, con spostamento massimo in sommità
pari a 8 mm per il telaio centrale e 0,3 mm per
quelli esterni.
E’ da notare che, sebbene la differenza in
termini relativi sia molto elevata, in termini
assoluti gli spostamenti risultano molto contenuti.
Con vincolo a cerniera tra tegoli e travi,
ovvero con diaframma perfettamente flessibile, si
hanno differenti risposte del telaio centrale e dei
telai esterni. La flessibilità del solaio comporta
risposte fuori fase con differenti spostamenti del
telaio centrale e dei telai esterni, che vibrano in
modo totalmente indipendente.
La storia di spostamento del telaio centrale si
sovrappone a quella dell’assetto isostatico,
mentre quella dei telai esterni riproduce il
comportamento a parete.
-­‐100
-­‐150
4.3
-­‐200
0
2
4
6
8
10
12
Tempo [s]
14
16
18
20
(b)
200
Telaio centrale
150
Telaio esterno
Spostamento [mm]
100
50
0
-­‐50
-­‐100
-­‐150
-­‐200
0
2
4
6
8
10
12
Tempo [s]
14
16
18
20
(c)
Figura 5. Storia di spostamento per edificio con assetto
isostatico; a) con piano rigido, b) con entrambe le nervature
dei tegoli connesse, c) con una sola nervatura connessa.
4.2
Assetto integrato
Le
curve
vibratorie
corrispondenti
all’applicazione
dell’accelerogramma
alla
struttura con assetto integrato dei pannelli con le
3 differenti tipologie di diaframma sono mostrate
in Figura 6.
L’edificio con diaframma perfetto di piano
mostra un comportamento estremamente rigido,
con uno spostamento massimo raggiunto pari a
0,36 mm.
Assetto dissipativo
Si considerano connessioni dissipative tra
pannelli, costituite da dispositivi ad attrito a
comportamento elasto-plastico con rigidezza
iniziale pari a 0,6 × 104 kN/m, e una forza limite
di scorrimento di 60 kN, ottenibile grazie alla
regolazione di apposite viti di serraggio.
I particolari del dispositivo (denominato
SPAV) sono descritti in Ferrara et al (2011) e
Biondini et al (2013).
Le curve vibratorie della struttura con
connessioni dissipative tra i pannelli sono
mostrate in Figura 7 per le 3 differenti tipologie
di diaframma.
L’edificio con diaframma rigido mostra un
comportamento intermedio, con spostamenti in
sommità pari a 13 mm, fortemente ridotti rispetto
al caso isostatico.
Con ipotesi di tegoli connessi rigidamente alle
travi, si ottengono curve vibratorie con profilo
simile, ma con spostamenti maggiori del telaio
centrale (17 mm) rispetto a quelli laterali (14
mm). L’effetto di diaframma di piano è rilevante,
sebbene la differenza tra gli spostamenti dei telai
non sia trascurabile.
Infine, con vincolo a cerniera tra tegoli e travi,
ovvero diaframma flessibile, il comportamento è
simile a quello dell’assetto integrato, con risposte
fuori fase e notevolmente differenti in termini di
spostamento.
0,4
Telaio centrale
Telaio esterno
0,3
Spostamento [mm]
0,2
0,1
0
-­‐0,1
-­‐0,2
-­‐0,3
-­‐0,4
0
2
4
6
8
10
Tempo [s]
12
14
16
18
20
(a)
8
Telaio centrale
Telaio esterno
6
Spostamento [mm]
4
2
0
-­‐2
-­‐4
-­‐6
-­‐8
-­‐10
0
2
4
6
8
10
Tempo [s]
12
14
16
18
20
(b)
200
Telaio centrale
Telaio esterno
150
Spostamento [mm]
100
50
0
-­‐50
-­‐100
-­‐150
0
2
4
6
8
10
Tempo [s]
12
14
16
18
20
(c)
Figura 6. Storia di spostamento per edificio con assetto integrato; a) con piano rigido, b) con entrambe le nervature dei tegoli
connesse, c) con una sola nervatura connessa.
In particolare, il telaio centrale e i telai esterni
vibrano in modo indipendente e la storia di
spostamento del telaio centrale si sovrappone a
quella dell’assetto isostatico, mentre quella dei
telai esterni riproduce il comportamento a parete.
E’ interessante notare che il massimo
spostamento in sommità del telaio esterno, pari a
6 mm, è notevolmente inferiore rispetto al
corrispondente spostamento con diaframma
rigido.
Il comportamento forza – spostamento delle
connessioni dissipative è mostrato in Figura 8. Se
per i casi di diaframma a) rigido e b) con grande
rigidezza si osservano ampi cicli dissipativi, per il
caso c) con diaframma flessibile si hanno cicli di
minore ampiezza, con limitata dissipazione.
20
Telaio centrale
Telaio esterno
15
Spostamento [mm]
10
5
0
-­‐5
-­‐10
-­‐15
-­‐20
0
2
4
6
8
10
Tempo [s]
12
14
16
18
20
(a)
20
Telaio centrale
Telaio esterno
15
Spostamento [mm]
10
5
0
-­‐5
-­‐10
-­‐15
-­‐20
0
2
4
6
8
10
Tempo [s]
12
14
16
18
20
(b)
200
Telaio centrale
Telaio esterno
150
Spostamento [mm]
100
50
0
-­‐50
-­‐100
-­‐150
-­‐200
0
2
4
6
8
10
Tempo [s]
12
14
16
18
20
(c)
Figura 7. Storia di spostamento per edificio con assetto dissipativo; a) con piano rigido, b) con entrambe le nervature dei tegoli
connesse, c) con una sola nervatura connessa.
Ciò indica che connessioni dissipative
applicate solo sulle pareti esterne di strutture con
telai interni richiedono un diaframma di elevata
rigidezza per attivare pienamente le loro capacità
di dissipazione energetica e limitare eccessive
deformazioni dell’edificio con distorsioni degli
orizzontamenti.
In Tabella 3 sono riportati i valori massimi di
sollecitazione per le diverse connessioni di un
pannello centrale, in particolare:
-
pannello – pannello
-
pannello – trave
-
pannello – fondazione
Nel caso di assetto isostatico, le reazioni
orizzontali dei fissaggi sono dovute agli effetti
del secondo ordine, mentre la reazione verticale
alla base del pannello è dovuta al peso proprio del
pannello. Nel caso di assetto integrato i valori di
forza sono di maggiore entità, sia per le
connessioni pannello-pannello, con valori fino a
109 kN, sia per le connessioni pannello-struttura,
con valori fino a 119 kN. Per l’assetto dissipativo
tali forze sono limitate dalla soglia di scorrimento
delle connessioni ad attrito.
80
60
40
Forza [kN]
20
0
-­‐20
-­‐40
-­‐60
-­‐80
-­‐5
-­‐4
-­‐3
-­‐2
-­‐1
0
1
Scorrimento [mm]
2
3
4
5
(a)
E’ interessante notare che il valore massimo
della forza raggiunto in assetto integrato con
tegoli incernierati sia sensibilmente inferiore
rispetto alle altre configurazioni con differenti
vincoli di piano.
In Tabella 5 sono infine riassunti i valori
massimi delle forze di taglio nelle connessioni
tegolo-trave, che risultano molto elevate nella
direzione longitudinale, ovvero nella direzione
del tegolo, con vincoli tegolo-trave rigidi e per i
casi di assetti non isostatici.
FORZA MASSIMA NELLE CONNESSIONI [kN]
80
ASSETTO VINCOLO PANNELLO-­‐
PANNELLI DI PIANO PANNELLO
60
40
RIGIDO
ISOSTATICO INCASTRO
CERNIERA
RIGIDO
INTEGRATO INCASTRO
CERNIERA
RIGIDO
DISSIPATIVO INCASTRO
CERNIERA
Forza [kN]
20
0
-­‐20
-­‐40
-­‐60
-­‐80
-­‐5
-­‐4
-­‐3
-­‐2
-­‐1
0
1
Scorrimento [mm]
2
3
4
0
0
0
98
109
54
60
60
60
7
7
7
83
98
42
48
55
45
64
64
64
64
64
64
64
64
64
6
6
6
107
119
64
69
68
69
5
Tabella 3. Forza massima nelle connessioni relative a un
pannello centrale per le diverse configurazioni.
(b)
80
FORZA MASSIMA NELLE CONNESSIONI [kN]
60
ASSETTO VINCOLO PANNELLO-­‐
PANNELLI DI PIANO PANNELLO
40
20
Forza [kN]
PANNELLO-­‐ PANNELLO-­‐ PANNELLO-­‐
TRAVE FONDAZIONE FONDAZIONE (ORIZZ.)
(VERT.)
(ORIZZ.)
0
-­‐20
-­‐40
-­‐60
-­‐80
-­‐5
-­‐4
-­‐3
-­‐2
-­‐1
0
1
Scorrimento [mm]
2
3
4
5
(c)
Figura 8. Cicli isteretici di una connessione ad attrito del
pannello centrale per edificio con assetto dissipativo; a) con
piano rigido, b) con entrambe le nervature dei tegoli
connesse, c) con una sola nervatura connessa.
In Tabella 4 sono riportati i valori massimi di
sollecitazione per le connessioni di un pannello
terminale. Per assetti non isostatici si hanno alla
base importanti reazioni verticali, con valori fino
a 261 kN, e limitate reazioni orizzontali. Questa
diversa distribuzione di forze rispetto al pannello
centrale è dovuta alla presenza di connessioni
pannello-pannello solo su un lato.
RIGIDO
ISOSTATICO INCASTRO
CERNIERA
RIGIDO
INTEGRATO INCASTRO
CERNIERA
RIGIDO
DISSIPATIVO INCASTRO
CERNIERA
0
0
0
78
85
54
60
60
60
PANNELLO-­‐ PANNELLO-­‐ PANNELLO-­‐
TRAVE FONDAZIONE FONDAZIONE (ORIZZ.)
(VERT.)
(ORIZZ.)
7
7
7
13
22
3
24
31
22
64
64
64
228
261
180
253
250
248
6
6
6
40
40
29
49
47
48
Tabella 4. Forza massima nelle connessioni relative a un
pannello terminale per le diverse configurazioni.
FORZA MASSIMA NELLE CONNESSIONI [kN]
ASSETTO PANNELLI
VINCOLO DI PIANO
RIGIDO
ISOSTATICO INCASTRO
CERNIERA
RIGIDO
INTEGRATO INCASTRO
CERNIERA
RIGIDO
DISSIPATIVO INCASTRO
CERNIERA
TEGOLO-­‐TRAVE TAGLIO LONGITUDINALE
TEGOLO-­‐TRAVE TAGLIO TRASVERSALE
-­‐
~ 16
~ 9
-­‐
~ 304
~ 20
-­‐
~ 234
~ 31
-­‐
~ 14
~ 10
-­‐
~ 36
~ 27
-­‐
~ 28
~ 29
Tabella 5. Forza massima nelle connessioni tegolo-trave
relative a un tegolo centrale per le diverse configurazioni.
5
CONCLUSIONI
In questo lavoro si è studiato il ruolo dell’azione
diaframma nel comportamento sismico di
strutture prefabbricate con pannelli di parete.
Edifici con piano flessibile sono in generale
caratterizzati da una diversa risposta sismica dei
telai che li compongono. In presenza di una
disomogenea distribuzione di massa e rigidezza,
dovuta ad esempio alla presenza di un assetto
integrato di connessione tra pannelli di
tamponamento e struttura, la risposta sismica può
dare luogo a notevoli distorsioni dell’impalcato.
In presenza di piano rigido il comportamento
sismico è in genere caratterizzato da elevate
sollecitazioni sugli elementi di piano e sulle
relative connessioni.
Questi aspetti sono stati esaminati con
riferimento a un tipico edificio prefabbricato
monopiano, caratterizzato da un telaio centrale e
due telai perimetrali con pannelli di parete. Sono
state svolte analisi dinamiche modali e non lineari
al variare delle caratteristiche delle connessioni di
diaframma e delle connessioni dei pannelli. I
risultati ottenuti hanno consentito di trarre le
seguenti conclusioni:
• una distribuzione omogenea di massa e
rigidezza comporta una risposta sismica
uniforme dei telai, che non impegna il
diaframma;
• con diaframma flessibile, una distribuzione
non omogenea di massa e rigidezza causa
significative distorsioni di piano e risposta
fuori fase dei telai, con un moto vibratorio che
risulta amplificato per i telai più flessibili e
ridotto per i più rigidi;
• con diaframma rigido, una distribuzione non
omogenea di massa e rigidezza comporta
elevate sollecitazioni sugli elementi del
diaframma e sulle loro connessioni;
• una distribuzione omogenea di rigidezza può
essere realizzata con un assetto di connessione
dei pannelli di tipo isostatico;
• un assetto di connessione dei pannelli non
isostatico (integrato o dissipativo) comporta
una disomogeneità di rigidezza tra telai esterni
e interni;
• un assetto di connessione dei pannelli di tipo
integrato comporta forze molto elevate nelle
connessioni;
• le forze nelle connessioni possono essere
limitate con un assetto di connessione dei
pannelli di tipo dissipativo;
• l’efficacia di un assetto dissipativo risulta
ridotta in edifici con diaframma flessibile.
Questi risultati evidenziano alcune delle
principali criticità nella progettazione di strutture
prefabbricate con pannelli di parete, in particolare
per il dimensionamento delle connessioni dei
pannelli di parete e degli elementi che realizzano
il diaframma di piano. Ulteriori approfondimenti
sono necessari per una estensione dei risultati
ottenuti a tipologie e configurazioni strutturali
diverse da quelle esaminate nel presente lavoro.
RINGRAZIAMENTI
Il presente studio è stato condotto nell’ambito delle finalità
del progetto di ricerca SAFECLADDING supportato da un
contributo della Commissione della Comunità Europea nel
programma FP7-SME-2011 con Grant agreement n. 314122
del 2012.
BIBLIOGRAFIA
Biondini, F., Dal Lago, B., Toniolo, G., 2013. Role of wall
panel connections on the seismic performance of precast
structures, Bulletin of Earthquake Engineering, 1-21,
2013, DOI: 10.1007/s10518-012-9418-z.
Biondini F.,Dal Lago B., Toniolo G., 2010. Influenza delle
connessioni tra pannelli sulla risposta sismica di
costruzioni prefabbricate, 18° Congresso CTE, Brescia,
11-13 novembre 2010.
Biondini F.,Dal Lago B., Toniolo G., 2012. Seismic
behaviour of precast buildings with cladding panels, 15th
World Conference of Earthquake Engineering, Lisbon,
Portugal, September 24-28, 2012.
Biondini F.,Dal Lago B., Toniolo G., 2011. Seismic
behaviour of precast structures with dissipative
connections of cladding wall panels, 14° Convegno
ANIDIS, Bari, 18-22 settembre 2011.
CEN-EN 1998-1:2004 2004. Eurocode 8: Design of
structures for earthquake resistance – Part 1 General
rules, seismic actions and rules for buildings, European
Committee for Standardization, Brussels, Belgium.
Ferrara, L., Felicetti, R., Toniolo, G., Zenti, C., 2011.
Friction dissipative devices for cladding panels in
precast buildings – an experimental investigation,
European Journal of Earthquake Engineering, 15(9),
1319–1338.
Ferrara, L., Toniolo, G., Tsionis, G., 2004. Sulla azione
diaframma dei sistemi di copertura in edifici industriali
prefabbricati in calcestruzzo armato, 15° Congresso
CTE, Bari, 4-6 novembre 2004.
Fleischman, R. B., Farrow, K. T., 2001. Dynamic response
of perimeter lateral-system structures with flexible
diaphragms, Earthquake Engineering and Structural
Dynamics, 30(5), 745–763.