L`accelerazione

L’accelerazione
Normalmente la velocità, durante un moto, non resta sempre costante ma può aumentare o diminuire. Per
comprendere in che modo la velocità cambia al trascorrere del tempo è utile introdurre un’altra grandezza
fisica: l’accelerazione media.
Consideriamo il seguente moto e calcoliamo la variazione di velocità Δv =v2 – v1 in ogni intervallo
Punti
tempo (sec)
Velocità
Δv = v2 – v1
O
0
A
1
B
5
C
10
D
15
E
20
0
3
6
15
15
3
3-0=3
6-3=3
15-6=9
15-15=0
3-15=-12
Adesso calcoliamo il rapporto tra la variazione di velocità e il tempo in cui avviene ogni variazione di
velocità
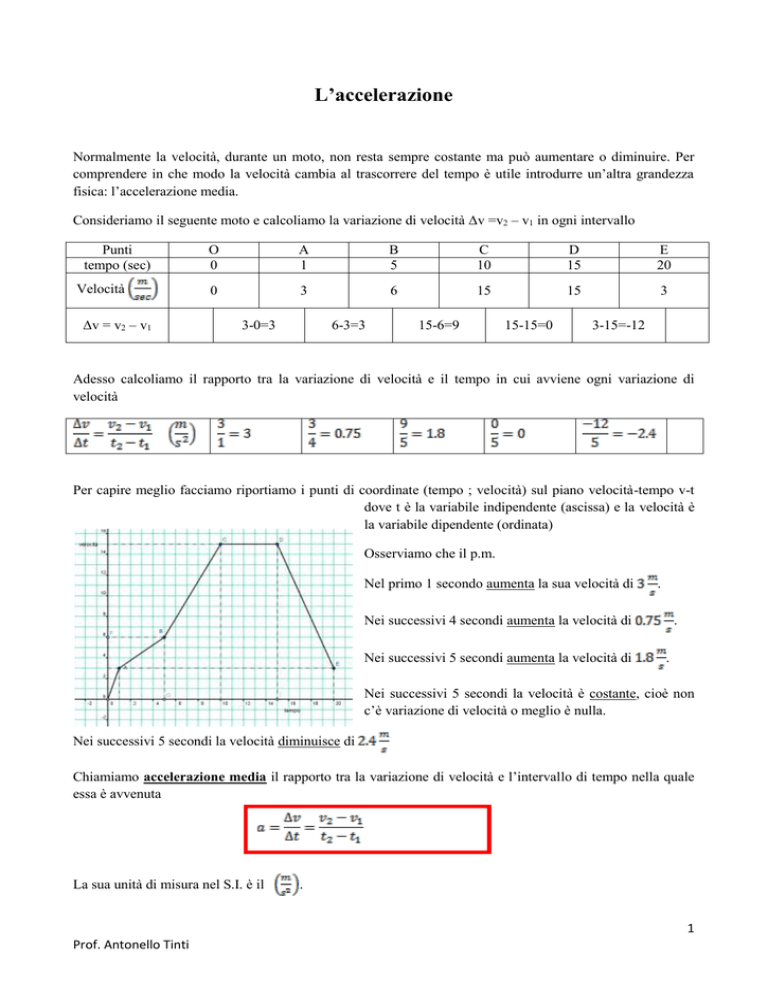
Per capire meglio facciamo riportiamo i punti di coordinate (tempo ; velocità) sul piano velocità-tempo v-t
dove t è la variabile indipendente (ascissa) e la velocità è
la variabile dipendente (ordinata)
Osserviamo che il p.m.
Nel primo 1 secondo aumenta la sua velocità di
.
Nei successivi 4 secondi aumenta la velocità di
Nei successivi 5 secondi aumenta la velocità di
.
.
Nei successivi 5 secondi la velocità è costante, cioè non
c’è variazione di velocità o meglio è nulla.
Nei successivi 5 secondi la velocità diminuisce di
Chiamiamo accelerazione media il rapporto tra la variazione di velocità e l’intervallo di tempo nella quale
essa è avvenuta
La sua unità di misura nel S.I. è il
.
1
Prof. Antonello Tinti
Quindi l’accelerazione, analogamente a quanto affermato per la velocità, è il coefficiente angolare (cioè la
pendenza) del segmento di retta.
Dire che un corpo ha una accelerazione di
significa dire la sua velocità cambia di
ogni secondo.
L’accelerazione può essere positiva, negativa o nulla; infatti poiche Δt = t2 – t1 >0 sempre, allora il segno
dell’accelerazione sarà determinato dal segno del numeratore Δv:
a>0
a<0
a=0
Δv>0
Δv<0
Δv=0
La velocità aumenta (moto accelerato)
La velocità diminuisce (moto ritardato) cioè il corpo rallenta
La velocità è costante (moto uniforme)
Analogamente a quanto fatto per la velocità, possiamo anche in questo caso definire l’accelerazione
istantanea, cioè l’accelerazione posseduta da un corpo in un certo istante.
Essa matematicamente è il limite a cui tende l’acclerazione media in un certo intervallo di tempo quando
l’intervallo stesso tende a zero.
Il moto rettilineo uniformemente accelerato (m.r.u.a.)
Definizione: un punto materiale si muove di m.r.u.a. quando la sua traiettoria è una linea retta e la sua
accelerazione è costante.
Consideriamo il seguente moto con parenza da fermo e riportiamo punti di coordinate (t;v) sul grafico
velocità-tempo
Punti
tempo (sec)
Velocità
O
0
A
1
B
3
C
5
D
7
E
9
0
2
6
10
14
18
Osserviamo che la pendenza della retta, cioè il rapporto tra la variazione
di velocità Δv (ordinata) e la variazione di tempo Δt (ascissa), è sempre
costante. Siamo in presenza di un m.r.u.a.
L’accelerazione media coincide con l’accelerazione istantanea am = ai e
quindi possiamo semplificare la notazione scrivendo
.
L’equazione oraria di questa retta sarà data da v = 2t
In generale
v = at
2
Prof. Antonello Tinti
Consideriamo il seguente moto con velocità iniziale non nulla
Punti
tempo (sec)
Velocità
O
0
A
1
B
2
C
3
D
4
E
5
2
5
8
11
14
17
Anche in questo caso siamo in presenza di un m.r.u.a. con velocità
iniziale non nulla.
L’equazione di questa retta sarà data da v = 3t + 2
In
generale
v = v0 + at
3
Prof. Antonello Tinti
La posizione nel m.r.u.a.
Consideriamo i primi 5 secondi in un moto rettilineo uniforme (v=costante) con velocità
Sul piano
velocità-tempo otteniamo una retta parallela all’asse dei tempi.
Ci chiediamo quale sarà lo spazio percorso. Dalla equazione oraria s = 9t
otteniamo s=45m
Osserviamo che tale valore corrisponde all’area del rettangolo sotteso dal
segmento di retta per t=5.
Attraverso il calcolo integrale si può dimostrare che l’area sottesa da un retta nel grafico velocità-tempo
rappresenta la misura dello spazio percorso in un m.r.u.a.
Si prenda il m.r.u.a. v = 3t + 2 già studiato in precedenza; ci chiediamo quale sarà lo spazio percorso dopo 4
secondi.
Consideriamo il suo grafico velocità-tempo
Evidenziamo l’area sottesa dal grafico per t=4 secondi, essa è un trapezio
rettangolo.
Calcoliamo l’area di tale trapezio
tale valore sarà lo
spazio percorso in 4 secondi.
4
Prof. Antonello Tinti
In generale spazio percorso Δs = s – s0 sarà dato da
Se il m.r.u.a. avviene con partenza da fermo v0 = 0 se t=0 e con
posizione iniziale nulla s0 = 0 allora la precedente diventa
Calcolo del tempo
Dalla
ricaviamoci il tempo t
Dalla
per ricavare il tempo dobbiamo risolvere l’equazione di II grado
nell’incognita t
5
Prof. Antonello Tinti