Introduzione

LICEO SCIENTIFICO STATALE
“GALILEO GALILEI”
Verona
ALGORITMI E PROBLEMI
Appunti sugli algoritmi e sulla programmazione in Pascal
1^ parte – Dagli algoritmi ai cicli
Dispensa realizzata dal prof. Paolo Gini ad uso degli studenti delle classi 1^ e 2^ del Liceo
Scientifico Tecnologico
1
INTRODUZIONE .................................................................................................................................. 2
PARTE PRIMA: I FONDAMENTI TEORICI............................................................................... 2
1
PROBLEMI E ALGORITMI .............................................................................................. 2
1.1
1.2
1.3
1.4
1.4.1
1.4.2
1.4.3
1.4.4
1.4.5
1.5
1.6
1.7
2
Cos’è un problema ........................................................................................................... 2
Risolutore ed esecutore .................................................................................................... 2
Algoritmi .......................................................................................................................... 3
Le capacità dell’esecutore ............................................................................................... 3
Memorizzare: le variabili............................................................................................. 3
Leggere informazioni (INPUT) .................................................................................... 4
Scrivere informazioni (OUTPUT) ................................................................................ 4
Calcolare espressioni matematiche ............................................................................. 5
Confrontare valori ed espressioni................................................................................ 5
Strutture di un algoritmo.................................................................................................. 6
Primo esempio di problema - algoritmo .......................................................................... 6
Esercizi ............................................................................................................................. 7
STRUTTURA DI UN ALGORITMO. DATI, ISTRUZIONI E STRUTTURE DI
CONTROLLO ............................................................................................................................... 7
2.1
2.2
2.3
2.3.1
2.3.2
2.3.3
2.3.4
2.3.5
2.4
2.5
Strutture di un algoritmo.................................................................................................. 7
Moduli o Unit ................................................................................................................... 9
Tipi di dati (semplici) ....................................................................................................... 9
Dati di tipo INTEGER ................................................................................................ 10
Dati di tipo REAL....................................................................................................... 10
Dati di tipo CHAR ...................................................................................................... 11
Dati di tipo BOOLEAN .............................................................................................. 11
Dati di tipo STRING................................................................................................... 11
Istruzioni Semplici: input, output, assegnazione ........................................................... 11
Istruzioni composte: strutture di controllo .................................................................... 13
3 STRUTTURE DI CONTROLLO ..................................................................................... 13
3.1
Sequenza......................................................................................................................... 13
3.2
Selezione o alternativa ................................................................................................... 13
3.2.1
Alternativa semplice ................................................................................................... 14
3.2.2
Sequenze all’interno dell’alternativa ......................................................................... 14
3.2.3
Selezioni nidificate (alternative di alternative) .......................................................... 15
3.2.4
L’istruzione CASE…OF ............................................................................................. 16
3.3
Iterazione ....................................................................................................................... 17
3.3.1
Il ciclo FOR…TO…DO .............................................................................................. 17
3.3.2
Il ciclo REPEAT …UNTIL ......................................................................................... 19
4
ESERCIZI ................................................................................................................................. 24
4.1
Esercizi (senza utilizzo di selezione e cicli) ................................................................... 24
4.2
Esercizi (richiedono l’utilizzo della selezione) .............................................................. 24
4.3
Esercizi (richiedono l’uso dell’iterazione) .................................................................... 24
4.4
Problemi vari (richiedono l’uso dell’iterazione e/ selezione) ....................................... 24
1
Introduzione
In questa dispensa saranno spiegati i concetti di problema e algoritmo, i metodi per rappresentare
gli algoritmi, come costruire e strutturare un algoritmo. Inoltre sarà introdotto il linguaggio di
programmazione Pascal.
La prima parte è essenzialmente teorica e presenta gli aspetti basilari della programmazione, seguiti
dai concetti fondamentali del linguaggio PASCAL; la seconda parte riprende i concetti teorici
sviluppandoli mediante problemi ed esercizi svolti. Una terza parte (prevista) conterrà gli elemnti
fondamentali dell’ambiente BORLAND TURBO PASCAL.
Parte prima: i fondamenti teorici
1
Problemi e algoritmi
1.1
Cos’è un problema
In generale, un problema è una situazione per la cui soluzione è necessario elaborare una
strategia cioè: organizzare le informazioni, le azioni da compiere, le scelte da fare.
I problemi che c’interessano sono quelli che possono essere affrontati traducendo il problema reale
in linguaggio matematico costruendo un modello matematico.
In tutte le situazioni problematiche che possono tradursi in un modello matematico esistono degli
elementi comuni:
 Esistono delle informazioni iniziali in nostro possesso o a cui possiamo accedere: dati e
relazioni fra i dati;
 Si deve costruire una procedura di risoluzione, elaborando i dati, riorganizzandoli e ricavando
da essi nuove informazioni;
 Attraverso l’elaborazione delle informazioni si perviene al risultato, cioè i dati finali.
1.2
Risolutore ed esecutore
Per risolvere un problema utilizzando l’informatica si ricorre al computer. Il computer è un
elaboratore che esegue operazioni sui dati. Il computer è un esecutore.
Dobbiamo distinguere fra il risolutore e l’esecutore.
 Il risolutore è colui che costruisce la procedura per risolvere il problema: l’attività
dell’esecutore è la programmazione.
 L’esecutore esegue le istruzioni programmate dal risolutore.
Il risolutore nello scrivere il programma dovrà seguire le seguenti fasi:






Individuare i dati iniziali;
Individuare i possibili metodi risolutivi (algoritmi);
Descrivere il procedimento risolutivo;
Codificare il procedimento risolutivo in un opportuno linguaggio di programmazione;
Far eseguire il programma dall’esecutore;
Verificare i risultati ottenuti.
2
Per eseguire le istruzioni prodotte dal risolutore, l’automa esecutore dovrà possedere le seguenti
capacità:


LEGGERE dati ricevuti dall’esterno (inseriti da tastiera,…)
SCRIVERE risultati, valori di espressioni e frasi (scrivere su monitor o su stampante numeri,
lettere, sequenze di lettere, risultati di calcoli,…);
 MEMORIZZARE dati, risultati, valori di espressioni;
 CALCOLARE espressioni aritmetiche;
 CONFRONTARE (stabilire se il risultato di un’espressione è vero o falso).
1.3
Algoritmi
I problemi risolvibili mediante un calcolatore (automa esecutore) richiedono che la procedura di
risoluzione abbia le seguenti caratteristiche:
 Le istruzioni sono eseguite una per volta, in ordine (sequenziale);
 La procedura ha un inizio e una fine e comporta un numero finito di passi (finita);
 In ogni punto della sequenza di istruzioni è ben determinata l’azione da compiere al passo
seguente (deterministica);
 Ogni istruzione deve poter essere eseguita in un tempo finito (effettivamente calcolabile).
Una procedura sequenziale, finita, deterministica, effettivamente calcolabile è chiamata algoritmo.
1.4
Le capacità dell’esecutore
Abbiamo affermato che, per svolgere il compito assegnato, l’automa esecutore deve possedere
alcune capacità; esaminiamo ora nel dettaglio tali capacità:
1.4.1 Memorizzare: le variabili
L’automa esecutore deve memorizzare i dati (numeri, caratteri, sequenze di caratteri) che deve
manipolare e i risultati dei calcoli. Per memorizzare le informazioni l’esecutore utilizza le
VARIABILI.
Variabile: oggetto identificato da un NOME e da un CONTENUTO (valore della variabile). In
informatica una variabile rappresenta uno spazio riservato in memoria. Una variabile è come una
scatola caratterizzata da un’etichetta (nome) e contenente un dato (valore) che può essere un
numero, una lettera, una sequenza di caratteri, un valore logico (vero-falso).
Ogni variabile può contenere dati di un solo tipo; nella maggior parte dei linguaggi di
programmazione è necessario dichiarare le variabili, cioè indicare il tipo di dati che possono
essere contenuti nella variabile (vedremo più avanti com’è possibile dichiarare le variabili nel
linguaggio PASCAL).
È bene ricordare che quando si modifica in qualche modo il contenuto di una variabile,
l’informazione sul valore precedente la modifica viene “dimenticato”, a meno che non sia
immagazzinato in un’altra variabile opportuna.
Inserire i dati in una variabile: ASSEGNAZIONE
Come si opera se si vuole “caricare” un valore in una variabile? Come si opera se si vuole
modificare il valore contenuto in una variabile?
3
L’istruzione che esegue tali compiti si chiama assegnazione: assegnare un valore ad una variabile
significa che, dopo l’assegnazione, la variabile conterrà il valore assegnato.
valore
valore
variabile
variabile
variabile
L’istruzione di assegnazione si scrive in modi diversi nei vari linguaggi di programmazione, per il
momento, in attesa di affrontare il linguaggio PASCAL, possiamo utilizzare il LINGUAGGIO DI
PROGETTO (pseudocodifica) e la rappresentazione mediante DIAGRAMMI DI FLUSSO
(diagrammi che usano forme geometriche, collegate da frecce, per rappresentare la sequenza delle
istruzioni):
Istruzione
Linguaggio di progetto
Assegnare alla variabile A il
valore x
Ax
Diagrammi di flusso
A:=x
1.4.2 Leggere informazioni (INPUT)
L’automa esecutore deve essere in grado di ricevere informazioni dall’esterno, cioè deve poter
LEGGERE dati; tali dati possono essere introdotti mediante tastiera o possono essere contenuti in
un file.
Quando l’automa riceve in input un dato, lo deve collocare in una variabile, quindi l’istruzione di
lettura deve indicare il nome della variabile in cui sarà collocato il dato, inoltre il tipo di dato “letto”
dovrà essere compatibile con il tipo di dati che possono essere contenuti dalla variabile.
L’istruzione di lettura può essere rappresentata nei modi seguenti:
Istruzione
Ricevere dall’esterno un valore
da attribuire alla variabile A
Linguaggio di progetto
Leggi (A)
Diagrammi di flusso
Leggi A
1.4.3 Scrivere informazioni (OUTPUT)
L’automa esecutore deve essere in grado di comunicare informazioni (risultati di elaborazioni)
dall’esterno, cioè deve poter SCRIVERE dati; tali dati possono essere scritti sul monitor, su
stampante, su di un file.
L’automa esecutore può mandare in output il valore contenuto in una variabile oppure un dato non
contenuto in una variabile; nel primo caso si deve indicare il nome della variabile di cui sarà scritto
il valore.
4
L’istruzione di lettura può essere rappresentata nei modi seguenti:
Istruzione
Scrivere sul dispositivo di
output il valore contenuto nella
variabile A
Scrivere sul dispositivo di
output la parola CIAO
Linguaggio di progetto
Diagrammi di flusso
Scrivi (A)
Scrivi A
Scrivi (“CIAO”)
Scrivi “CIAO”
1.4.4 Calcolare espressioni matematiche
L’automa esecutore deve essere in grado di eseguire calcoli sui dati numerici; il tipo di operazioni
che l’automa è in grado di compiere dipende dal tipo di dati numerici su cui opera.
È fondamentale ricordare che i numeri sono memorizzati, dall’automa, nelle variabili, le quali
rappresentano spazi riservati nella memoria fisica del calcolatore; poiché lo spazio disponibile in
memoria è ovviamente finito, è evidente che qualsiasi numero sarà memorizzato con un numero
limitato di cifre decimali e che i numeri reali (che hanno infinite cifre decimali) saranno
approssimati.
I simboli utilizzati per le operazioni aritmetiche sono quelli usuali; per quanto riguarda le funzioni
rimandiamo alla parte sul PASCAL le specifiche.
Il risultato di una o più operazioni deve essere memorizzato in una variabile, quindi possiamo per
ora indicare questi tipi di simbologie:
Istruzione
Calcola la somma dei valori
contenuti in A e B e memorizza
in C
Calcola il prodotto di A, B, 4 e
lo memorizza in A (sostituendo
il risultato al valore precedente)
Linguaggio di progetto
Diagrammi di flusso
CA+B
C:=A+B
A4*A*B
A:=4*A*B
1.4.5 Confrontare valori ed espressioni
L’automa esecutore deve essere in grado di confrontare valori o espressioni, ossia:
 Confrontare due numeri/espressioni e stabilire se la prima è maggiore/minore/uguale alla
seconda;
 Stabilire se una data condizione è vera o è falsa.
Gli operatori di confronto sono gli stessi del linguaggio matematico: >, <, =.
Quando l’esecutore confronta due espressioni il risultato del confronto è il valore di una variabile di
tipo LOGICO (BOOLEANA), tale tipo di variabile può assumere due soli valori: vero, falso.
Ad esempio la frase “5 è maggiore di 7” ha un valore logico falso.
Approfondiremo l’utilizzo del confronto e delle variabili logiche nella sezione specifica per il
PASCAL.
5
1.5
Strutture di un algoritmo
In un algoritmo possiamo distinguere due parti:
 Parte dichiarativa: in questa parte si devono indicare (dichiarare) tutti gli oggetti (variabili)
che saranno utilizzati nell’algoritmo; per ciascun oggetto si dovrà dichiarare il NOME e il TIPO
(ad esempio se si tratta di un numero intero, di un carattere, di una sequenza di caratteri,…).
Questo passaggio è fondamentale, l’automa esecutore deve essere informato di tutti gli oggetti
che dovrà manipolare e delle loro caratteristiche.
 Parte esecutiva: è la parte dell’algoritmo in cui si eseguono le istruzioni sulle variabili.
1.6
Primo esempio di problema - algoritmo
Consideriamo un semplice problema di geometria elementare e analizziamo come possiamo
tradurlo in un algoritmo e rappresentarlo.
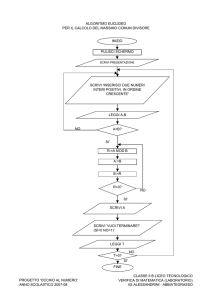
Problema: Calcolare l’area di un rettangolo, essendo note la base e l’altezza.
I dati iniziali sono: il valore della base, il valore dell’altezza. Inoltre conosciamo la relazione che
permette di calcolare l’area del rettangolo.
La procedura (parte esecutiva) può essere schematizzata nel modo seguente:
a)
LEGGI i valori dell’altezza e della base (l’automa deve acquisire i dati);
b)
CALCOLA L’AREA;
c)
SCRIVI il risultato (l’automa deve restituire il risultato).
La procedura può essere rappresentata con un diagramma di flusso nel seguente modo:
inizio
Leggi(B,H)
AREA:=B*H
Scrivi(AREA)
fine
Utilizzando il linguaggio di progetto, le istruzioni sono codificate nel modo seguente:
inizio
leggi (B, H)
AREAB*H
Scrivi (AREA)
{legge i valori di B e H immessi da tastiera e li memorizza}
{assegna alla variabile AREA il valore di B*H}
{scrive sul dispositivo di output il valore di AREA}
fine.
6
1.7
Esercizi
Rappresenta con il diagramma di flusso e con il linguaggio di progetto gli algoritmi che risolvono i
seguenti problemi:
1. Noti i cateti determinare l’area e il perimetro di un triangolo rettangolo;
2. Noti due numeri x e y, determinare la loro media;
3. Un noleggio di automobili applica le seguenti tariffe: 75 euro di spesa fissa più 0.5 euro per ogni
km percorso. Calcolare la spesa del noleggio.
2
Struttura di un algoritmo. Dati, istruzioni e strutture di
controllo
Abbiamo già visto che in un algoritmo distinguiamo due parti: la parte dichiarativa, in cui sono
definite tutte le variabili e le costanti che saranno utilizzate, e la parte esecutiva, in cui sono presenti
le istruzioni che l’esecutore dovrà eseguire. In questo capitolo:
 analizzeremo in dettaglio la struttura di un algoritmo e la sua codifica in Pascal;
 chiariremo il significato di variabile e ne illustreremo i vari tipi;
 analizzeremo in dettaglio le istruzioni.
2.1
Strutture di un algoritmo
Un programma scritto in un linguaggio strutturato (PASCAL, Linguaggio di progetto, …) ha una
struttura formata da tre parti.
Intestazione
Sezione
Dichiarativa
Corpo del
programma
 INTESTAZIONE
In un programma la prima riga contiene l’intestazione, formata da una sola riga.
Nel linguaggio PASCAL, l’intestazione inizia con la parola chiave program seguita dal nome del
programma (il nome del programma può essere diverso dal nome del file in cui è memorizzato il
programma). Al termine della riga di intestazione deve esserci il simbolo ; (punto e virgola) che
indica il termine dell’istruzione.
program nome;
{è necessario terminare la riga con il punto e virgola (;) }
 SEZIONE DICHIARATIVA
Dopo l’intestazione deve essere inserita la sezione dichiarativa, ossia la parte in cui sono definiti
(cioè viene assegnato un nome e un tipo) tutti gli oggetti su cui opera l’algoritmo, cioè:
 Costanti
 Variabili
 Tipi di dati non predefiniti (non necessari per primi semplici programmi)
7

□
Procedure e funzioni (non necessari per primi semplici programmi)
Costanti
In alcuni programmi è utile usare dei dati costanti, in altre parole dei dati il cui valore non
cambia durante l’esecuzione del programma. Ad esempio, se in un programma si ha che fare
con cerchi e circonferenze è utile avere una costante che contenga il valore di .
Si possono dichiarare come costanti: numeri e stringhe (sequenza di caratteri, lettere e/o
numeri e/o simboli racchiusi fra due apici).
In PASCAL la dichiarazione delle costanti deve precedere le altre e ha la seguente sintassi:
CONST nome_costante = valore;
□
Variabili
Di tutte le variabili che saranno utilizzate è necessario dichiarare il nome e il tipo (cioè
l’insieme di valori che può assumere).
In PASCAL la dichiarazione delle variabili ha la seguente sintassi:
VAR nome_variabile: tipo_variabile;




Nome_variabile: indica il nome che viene dato ad una variabile
Tipo_variabile: indica il tipo di variabile (integer = intero, real = razionale, char =
carattere, string = sequenza di caratteri, boolean = logica).
Dopo il nome della variabile deve essere inserito il simbolo due punti (:)
Si possono elencare più variabili di uno stesso tipo separandole con una virgola.
I nomi delle variabili (e di tutti gli oggetti) sono detti identificatori e possono essere composti da
un massimo di 127 caratteri (senza lo spazio), di cui però solo i primi 8 vengono considerati.
 CORPO DEL PROGRAMMA
Il corpo del programma contiene la sequenza d’istruzioni che devono essere eseguite per risolvere il
problema che si sta affrontando.
Il corpo del programma deve essere in qualche modo delimitato, nel caso del linguaggio PASCAL è
racchiuso fra le parole BEGIN e END. (si noti il punto dopo END!) che funzionano come parentesi
(se si utilizzano i diagrammi di flusso, il corpo del programma è delimitato da due ovali contenenti
le parole inizio e fine):
 Tutte le istruzioni devono terminare con il simbolo ; (punto e virgola), ad eccezione
dell’ultima istruzione che precede END (per la quale è facoltativo).
 Con programmi complessi si rende necessario l’uso di blocchi di istruzioni annidati
all’interno del blocco principale. Questi blocchi saranno delimitati dalle istruzioni BEGIN
(inizio blocco) e END (fine blocco) senza il punto finale. I diversi blocchi possono essere
evidenziati graficamente usando l’indentazione.
8
BEGIN
Istruzione 1;
istruzione 2;
BEGIN
{INIZIO SOTTO –BLOCCO}
Istruzione 4;
Istruzione 4
END;
{FINE BLOCCO - SI NOTI IL PUNTO E VIRGOLA}
Istruzione 5;
BEGIN
{INIZIO SOTTO –BLOCCO}
Istruzione 6;
Istruzione 7
END
{FINE SOTTO-BLOCCO}
END.
2.2
Moduli o Unit
Il linguaggio PASCAL possiede molte istruzioni. Le più comuni (come BEGIN, END, WRITELN,
ecc) sono presenti direttamente nel programma principale, altre, che si utilizzano solo per scopi
particolari, sono raggruppate in “librerie” (cioè in files accessori) chiamate moduli o unit, ciascuna
individuata da un nome.
Ad esempio ci sono unit che ottimizzano la gestione della grafica, altre che ottimizzano la gestione
dello schermo o della stampante.
Per poter utilizzare le istruzioni raggruppate in una unit è necessario informare preliminarmente il
compilatore; per farlo si deve inserire subito dopo l’intestazione l’istruzione:
USES nome_unit1,nome_unit2,…;
Le più importanti unit sono:
 CRT
contiene istruzioni per gestione dello schermo;
 PRINT
contiene istruzioni per gestione della stampante;
 GRAPH
contiene istruzioni per gestione della grafica (cioè per eseguire disegni)
2.3
Tipi di dati (semplici)
I dati che possono essere utilizzati in un programma scritto in PASCAL si possono classificare in
due categorie principali:
 SEMPLICI (è definito un ordine all’interno dei valori permessi)
o INTEGER
o REAL
o CHAR
o BOOLEAN
Esistono anche altri tipi di variabili semplici, ma sono utilizzati per programmazione avanzata e
la loro trattazione non rientra negli scopi di questa dispensa.
 STRUTTURATI
o STRING
o ARRAY
o SET
o RECORD
o FILE
Per il momento ci occuperemo solo dei dati di tipo semplice e del tipo STRING.
9
2.3.1 Dati di tipo INTEGER
I dati di tipo INTEGER costituiscono un sottoinsieme dei numeri interi Z con valori compresi fra
–32768 e +32767. Un numero di tipi INTEGER viene memorizzato usando 16 bit (2 byte), un bit
per il segno e 15 per il valore, quindi si possono avere 215 possibili valori (ogni bit può assumere
valore 0 o 1).
In questo insieme si possono eseguire le seguenti operazioni:
Operazione
Addizione
Sottrazione
Moltiplicazione
Divisione intera
Resto
Simbolo
+
*
DIV
MOD
Note
Restituisce il quoziente intero (Es: 15 DIV 2 = 7)
Restituisce il resto della divisione (Es: 17 MOD 6 = 5)
Attenzione! Se nel corso dell’elaborazione una variabile INTEGER assume valori fuori
dell’intervallo ammesso, non viene segnalato alcun errore; ad esempio se si cerca di calcolare
32760 + 20, si supera il valore massimo (32767) e si ricomincia dal valore minimo (-32768) 
32760 + 20 = -32756!
Nell’insieme INTEGER sono disponibili alcune funzioni predefinite (istruzioni che forniscono
come risultato un solo valore):
ABS(X)
Calcola il valore assoluto del numero contenuto nella variabile X
SQR(X)
Calcola quadrato del numero contenuto nella variabile X
SUCC(X)
Calcola successore del numero contenuto nella variabile X
PRED(X)
Calcola precedente del numero contenuto nella variabile X
2.3.2 Dati di tipo REAL
È costituito da un sottoinsieme dei numeri razionali Q i cui valori assoluti sono compresi
nell’intervallo: 2.910-39; 1.71038. Un dato di tipo REAL è memorizzato usando 6 bytes (48 bit),
ha 11 cifre significative e normalmente viene scritto in notazione esponenziale con una sola cifra
intera diversa da zero (ad esempio: -123.4567 è scritto nella forma -1.2345670000E+02 che
corrisponde alla notazione matematica –1.234567102).
Quando viene scritto su video o carta in Turbo Pascal, un numero di tipo REAL occupa 18 spazi (1
per il segno, 1 per la cifra intera, 1 per il punto decimale, 10 per la parte decimale, 1 per la lettera E,
1 per il segno dell’esponente, 2 per l’esponente); il modo in cui il numero viene scritto può essere
modificato utilizzando l’istruzione WRITE o WRITELN nel modo seguente:
WRITELN(a:n:d)
 scrive il valore della variabile a, usando n posti e con d cifre decimali.
In questo insieme si possono eseguire le seguenti operazioni:
Operazione
Addizione
Sottrazione
Moltiplicazione
Divisione
Simbolo
+
*
/
Note
10
Nell’insieme REAL sono disponibili alcune funzioni predefinite (istruzioni che forniscono come
risultato un solo valore):
ABS(X)
Calcola il valore assoluto del numero contenuto nella variabile X
SQR(X)
Calcola il quadrato del numero contenuto nella variabile X
SQRT(X)
Calcola la radice quadrata di un numero non negativo
Attenzione! I numeri di tipo REAL sono comunque numeri razionali con un numero finito di cifre,
quindi nei calcoli si producono facilmente errori dovuti all’approssimazione che il calcolatore
compie nel rappresentare i numeri.
2.3.3 Dati di tipo CHAR
I dati di tipo CHAR corrispondono ai caratteri che si possono introdurre da tastiera compreso lo
“spazio”.
Gli oggetti di tipo char devono sempre essere racchiusi fra due apici.
In questo insieme non sono definite operazioni, ma sono definite alcune funzioni:
CHR(n)
Se n è un numero INTEGER, chr(n) restituisce il corrsipondente carattere nel
codice ASCII
ORD(car)
Se car è un carattere ord(car) restituisce il corrispondente numero nel codice
ASCII
2.3.4 Dati di tipo BOOLEAN
L’insieme BOOLEAN è un insieme non numerico che contiene solo due elementi: TRUE (vero),
FALSE (falso), quindi una variabile definita come boolean potrà assumere solo i valori vero e
falso.
Le variabili boolean sono utilizzate soprattutto nelle condizioni da controllare nelle istruzioni di
selezione.
2.3.5 Dati di tipo STRING
I dati di tipo STRING sono formati da sequenze (stringhe) di caratteri, con lunghezza massima n.
Quando si dichiara una variabile di tipo string si deve indicare il numero massimo di caratteri (n);
la scrittura da utilizzare è la seguente:
VAR nome_variabile: STRING[n];
ove n è un numero intero minore o uguale a 255.
2.4
Istruzioni Semplici: input, output, assegnazione
Come analizzato nel primo capitolo, l’automa esecutore, per svolgere il proprio compito, deve
essere in grado di eseguire istruzioni semplici = istruzioni che descrivono una sola azione
elementare.
Le istruzioni semplici sono:
 Leggere valori dall’esterno e memorizzarli
 Scrivere risultati o valori di espressioni;
 Assegnare valori di espressioni a variabili.
Nel linguaggio PASCAL queste istruzioni semplici sono:
11
Istruzione
leggere
scrivere
assegnare
PASCAL
Read(variabile1, variabile2,…) Readln(variabile1, variabile2,…)
Write(variabile1, variabile2,…) Writeln(variabile1, variabile2,…)
nomevariabile:=espressione
Ove: variabile1, variabile2,… sono i nomi di variabili.
□ Istruzioni di lettura. Le istruzioni read e readln permettono all’automa esecutore di
“leggere” valori forniti dall’esterno (nel caso più semplice si tratta di dati inseriti mediante la
tastiera). Queste due istruzioni differiscono perché dopo l’esecuzione dell’istruzione readln
il programma “va a capo” mentre dopo read il cursore rimane sulla stessa riga.
I nomi delle variabili i cui valori devono essere letti devono essere racchiusi tra parentesi
tonde e devono essere separati dalla virgola.
L’istruzione readln può essere utilizzata da sola (cioè senza variabili da leggere inserite fra
parentesi) per interrompere l’esecuzione del programma sino a che l’operatore non prema un
qualsiasi tasto.
□ Istruzioni di scrittura. Le istruzioni write e writeln permettono all’automa esecutore di
“scrivere”, cioè di fornire risultati in output. Mediante queste due istruzioni è possibile
scrivere sul dispositivo di output standard (normalmente lo schermo) risultati di calcoli,
messaggi, ecc. Le due istruzioni differiscono per il fatto che dopo l’esecuzione dell’istruzione
writeln il programma “va a capo” mentre dopo write il cursore rimane sulla stessa riga.
Le istruzioni write e writeln richiedono che siano inseriti tra parentesi tonde, separati da
virgole, i nomi delle variabili di cui devono essere scritti i valori; è possibile anche scrivere
direttamente dei caratteri, delle stringhe o delle frasi, inserendoli fra apici (‘stringa’).
Esempi:
writeln(A)  scrive sullo schermo il valore della variabile A.
writeln(‘AAA’) scrive sullo schermo la sequenza di caratteri AAA.
Writeln(‘Il valore di A è ‘,A)scrive sullo schermo: Il valore di A è seguito dal valore di A
□ Istruzione di assegnazione. L’istruzione di assegnazione permette di assegnare ad una
variabile un valore. Il valore da assegnare può essere ottenuto mediante il calcolo di
un’espressione, o può essere un valore (numerico o d’altro tipo) già stabilito. La sintassi di
questa istruzione prevede che si scriva a sinistra il nome della variabile, seguito dal simbolo
:= (due punti uguale) che rappresenta l’assegnazione e dal valore che si vuole assegnare (o
dall’espressione il cui risultato deve essere assegnato alla variabile).
Esempi:
A:=7  assegna alla variabile A il valore 7.
A:=’Pippo’  assegna alla variabile A (di tipo string) il valore Pippo.
A:=B*8-5/2  assegna alla variabile A il risultato dell’espressione a destra.
A:=A+1  calcola il risultato dell’espressione A+1 e poi lo assegna ad A.
12
2.5
Istruzioni composte: strutture di controllo
Le istruzioni composte sono istruzioni che si realizzano combinando azioni elementari. Le
istruzioni composte sono dette anche strutture di controllo.
Le strutture di controllo sono tre:

Struttura di SEQUENZA: è costituita da una successione di istruzioni (semplici o composte)
da eseguire in un ordine stabilito. L’insieme di queste istruzioni si chiama blocco di istruzioni
(è necessario indicare all’esecutore l’inizio e la fine del blocco)

Struttura di SELEZIONE o ALTERNATIVA: quest’istruzione consiste nella scelta fra due
istruzioni alternative; la scelta è effettuata in base al verificarsi o meno di una condizione
(confronto)

Struttura d’ITERAZIONE: consiste nel ripetere un’istruzione o un blocco d’istruzioni più
volte. Il numero di ripetizioni è effettuato mediante un confronto.
Teorema di Boom – Jacopini:
Qualsiasi algoritmo è sempre riconducibile ad un algoritmo contenente solamente le strutture di
iterazione, di selezione e di sequenza.
Vedremo nei paragrafi successivi come si rappresentano in PASCAL queste strutture.
3
Strutture di controllo
3.1
Sequenza
La struttura di sequenza è estremamente semplice; le istruzioni sono disposte una di seguito
all’altra, separate dal simbolo punto e virgola (;).
In una sequenza le istruzioni possono essere sia semplici sia composte, quindi all’interno di una
sequenza possono essere presenti strutture di selezione e di iterazione.
Esempio:
writeln(‘INSERISCI UN NUMERO INTERO’);
readln(A);
writeln(‘Il valore di A è ‘,A);
3.2
Selezione o alternativa
In molti casi è necessario scegliere fra due o più istruzioni (o sequenze di istruzioni) in base ad una
condizione. Ad esempio potremmo voler scrivere un programma che restituisca il valore assoluto di
un numero inserito da tastiera; in questo caso il programma, una volta letto il numero, dovrà
eseguire una certa sequenza di istruzioni se il numero introdotto è positivo o nullo, mentre dovrà
eseguire un’altra sequenza se il numero è negativo. L’istruzione composta che permette di fare ciò
si chiama alternativa.
13
3.2.1
Alternativa semplice
Il più semplice tipo di selezione si presenta nella seguente forma:
se condizione allora istruzione1 altrimenti istruzione2
L’esecutore controlla la condizione (cioè controlla se è VERA o se è FALSA), quindi esegue
l’istruzione1 se la condizione è vera, altrimenti esegue l’istruzione2.
La selezione semplice è rappresentata in un diagramma di flusso nel seguente modo:
Vera
condizione
Falsa
Istruzione2
Istruzione1
Nel linguaggio PASCAL la selezione semplice si presenta con la seguente sintassi:
IF condizione THEN istruzione1
ELSE istruzione2;
Si noti che l’istruzione termina solo con il punto e virgola finale.
Esercizi
1. Scrivi un programma che, letto un numero intero da tastiera, riconosca se è un multiplo di 3
o no.
3.2.2
Sequenze all’interno dell’alternativa
In molti casi è necessario eseguire più istruzioni in un’alternativa; in questi casi il blocco di
istruzioni da eseguire deve essere racchiuso fra le parole BEGIN e END.
IF condizione THEN
BEGIN
Istruzione1;
Istruzione2;
…..
IstruzioneN
END
ELSE
BEGIN
Istruzione1;
Istruzione2;
…..
IstruzioneN
END;
Si noti che:
 Le istruzioni contenute in un blocco e
racchiuse fra BEGIN e END terminano
tutte con il “;”, tranne quella che precede
l’END.
 La sequenza IF … THEN … ELSE
termina con il “;” dopo l’END.
14
ESEMPI
Program area;
var lato, perimetro, area: integer;
BEGIN
write(‘Scrivi la misura del lato: ‘);
readln(lato);
IF lato<0 THEN
write(‘dato non valido’)
ELSE
BEGIN
Perimetro:=4*lato;
area:=lato*lato;
writeln(‘perimetro = ‘,perimetro);
writeln(‘area = ‘,area)
END
END.
Si noti che:
 Per calcolare il quadrato
abbiamo usato lato*lato.
 Se lato<0 èVERA si esegue
solo l’istruzione che scrive il
messaggio d’errore;
 Se lato<0 è FALSA si esegue
solo il blocco compreso fra
BEGIN e END dopo l’ELSE.
Esercizi
1. Scrivi un programma che, letto un numero intero da tastiera, ne calcoli la seconda, la terza e
quarta potenza se il numero è diverso da zero, altrimenti emetta un messaggio d’errore.
2. Scrivi un programma che, letto un numero intero da tastiera, ne scriva l’opposto e ne calcoli
il quadrato, se il numero è positivo, altrimenti ne calcoli il valore assoluto.
3. Scrivi un programma che, letto un numero intero n da tastiera, calcoli n/2 se il numero è
pari, altrimenti (n-1)/2.
4. Scrivi un programma che, lette le misure di tre angoli, stabilisca se si tratta degli angoli di
un triangolo.
5. Scrivi un programma che, lette le misure dei lati di un triangolo stabilisca se si tratta di un
triangolo isoscele, equilatero o scaleno.
6. Scrivi un programma che, lette le misure dei lati di un triangolo, stabilisca se si tratta di un
triangolo rettangolo.
7. Scrivere un programma che, letti tre numeri, stabilisca il minore di essi.
8. Scrivere un programma che , letto il prezzo di un elettrodomestico, calcoli il prezzo
scontato, sapendo che il tasso di sconto è del 10% se il prezzo è inferiore a 500 euro, e del
15% se il prezzo è superiore a 500 euro.
9. Scrivere un programma che, letti due numeri, controlli se il secondo è multiplo del primo.
3.2.3
Selezioni nidificate (alternative di alternative)
Il costrutto IF…THEN…ELSE consente di scegliere fra due alternative, ma in molti casi è
necessario scegliere fra più di due alternative, oppure si rende necessario operare una scelta
all’interno di un blocco di istruzioni racchiuso in un’alternativa; in questi casi si possono utilizzare
le selezioni nidificate. Poiché l’alternativa è un’istruzione è possibile inserirla all’interno di un
blocco d’istruzioni come mostrato qui di seguito:
15
IF condizione1 THEN
BEGIN
Istruzione1;
IF condizione2 THEN
BEGIN
Istruzione2;
Istruzione3
END
ELSE
BEGIN
Istruzione4;
Istruzione5
END
END
ELSE
Istruzione6;
Condizione1
V
F
Istruzione6
Istruzione1
Condizione2
Istruzione2
Istruzione3
Istruzione4
Istruzione5
Esercizi
1. Scrivi un programma che, letto un numero reale da tastiera, scriva sullo schermo se il
numero è positivo, negativo o nullo.
2. Scrivi un programma che visualizzi sullo schermo il tuo nome o il tuo cognome in base al
valore di una variabile di nome “scelta” di tipo string. Se tale variabile non assume i valori
“nome” o “cognome” il programma deve restituire un messaggio d’errore.
3. Scrivi un programma che, letto due numeri reali da tastiera, permetta di scegliere se
calcolare il prodotto, il quoziente, la somma o la differenza secondo il simbolo di operazione
introdotto.
3.2.4
L’istruzione CASE…OF
In alcuni casi si presenta la necessità di scegliere fra più possibilità alternative (come nell’esercizio
3 del paragrafo precedente); in questi casi anziché il costrutto IF …THEN…ELSE è possibile
utilizzare l’istruzione CASE…OF.
Per utilizzare questa istruzione è necessario definire una variabile di cui andrà controllato il valore,
indicandone il tipo.
L’istruzione ha questa sintassi:
case nome_variabile of
valore1: istruzione1;
valore2: istruzione2;
valore3: istruzione3
else istruzione 4
end;
 l’istruzione controlla il valore della variabile nome_variabile
 se il valore coincide con valore1 esegue istruzione1;
 se il valore coincide con valore1 esegue istruzione2;
 se il valore coincide con valore1 esegue istruzione3;
 se non coincide con nessuno esegue istruzione4;
 l’istruzione case deve terminare con la parola end
se al posto di un’istruzione c’è un blocco d’istruzioni, deve essere
racchiuso fra begin e end
16
3.3
Iterazione
Molto spesso è necessario ripetere più volte la stessa istruzione o la stessa sequenza di istruzioni; la
struttura di controllo che esegue questo tipo di operazione è chiamata iterazione.
In generale, nella programmazione, possiamo trovare tre tipi di iterazione:

Iterazione enumerativa: consiste nella ripetizione di un gruppo di istruzioni per un numero
fissato di volte.
 Iterazione per falso: consiste nel ripetere una sequenza di istruzioni fino a quando una data
condizione non assume valore VERO.
 Iterazione per vero: consiste nel ripetere una sequenza di istruzioni fintantoché una condizione
di controllo rimane VERA.
Nel linguaggio PASCAL i tre tipi di iterazione sono codificati dalle istruzioni:
 FOR … TO … DO
 REPEAT …UNTIL
 DO…WHILE
3.3.1
Il ciclo FOR…TO…DO
Questo tipo di ciclo permette di eseguire ripetutamente istruzioni quando si sappia il numero di
volte che si desidera ripetere il ciclo. La struttura sintattica è la seguente:
for nome_variabile:=valore iniziale to valore finale do
begin
istruzione 1;
istruzione 2;
istruzione n
{non c’è il “;”}
end;
Nella struttura riportata nome_variabile rappresenta la variabile che conta il numero di esecuzioni
(prende il nome di contatore) del ciclo e và dal valore iniziale sino al valore finale.
Analizziamo come opera la struttura FOR …TO…DO:
 Quando raggiunge la parola FOR, il programma assegna al contatore un valore pari a
valore_iniziale (per esempio 1);
 Quindi il programma esegue le istruzioni comprese fra la parola BEGIN e la parola END
 Poi il programma torna a FOR e incrementa nome_variabile di 1;
 Il programma controlla se nome_variabile ha superato valore_finale; se valore_finale non è
stato superato, il programma ripete la sequenza fra BEGIN e END; se valore_finale è stato
superato, il programma passa all’istruzione successiva all’END.
17
Consideriamo il seguente esempio:
program ciclo1;
{Questo programma calcola la somma dei primi N numeri naturali}
var N,S,I; integer;
{notare che il contatore I deve essere dichiarato!}
begin
writeln(‘Inserisci il numero N di numeri di cui calcolare la somma’);
readln(N);
S:=0;
{la variabile S conterrà la somma e deve essere inizializzata a 0}
for I:=1 to N do
begin
S:=S+I
end;
writeln(‘La somma dei primi ‘,N,’ numeri naturali è ‘,S);
readln
end.
Supponiamo che alla richiesta di inserire il valore di N si digiti il numero 3; il programma esegue i
seguenti passi a partire dal FOR:
passo 1
Assegna a S il valore 0
Passo 2
Assegna a I il valore 1
Passo 3
Assegna a S il valore S+I  S = 0+1 = 1
Passo 4
Assegna a I il valore I+1  I = 2; controlla se I>3 (FALSO  prosegue)
Passo 4
Assegna a S il valore S+I  S = 1+2 = 3
Passo 5
Assegna a I il valore I+1  I = 3; controlla se I>3 (FALSO  prosegue)
Passo 6
Assegna a S il valore S+I  S = 3+3
Passo 7
Assegna a I il valore I+1  I = 4; controlla se I>3 (VERO  termina)
Passo 8
Il valore ottenuto per S è 6 e tale numero viene scritto in output
Esercizi
1. Scrivi un programma che, letto un numero intero N da tastiera, scriva sullo schermo il
prodotto dei primi N numeri naturali (escluso lo 0); fai una tabella per analizzare l’output
nel caso N sia pari a 5.
18
3.3.2
Il ciclo REPEAT …UNTIL
In molti casi non è possibile conoscere a priori il numero di volte che un ciclo deve essere eseguito.
In queste situazioni, è possibile fissare una condizione di controllo, e far ripetere il ciclo sino a
quando la condizione non diventa vera oppure fino a quando non diventa falsa.
Il ciclo repeat…until… (ripeti…finchè…) consente di ripetere una sequenza di istruzioni sino al
momento in cui una data condizione non diventa vera. Nel ciclo repeat …until… il controllo sulla
verità è effettuato alla fine della sequenza di istruzioni.
La struttura può essere rappresentata mediante il seguente diagramma di flusso:
Istruzione 1
Istruzione 1
Istruzione 1
condizione
falsa
vera
In PASCAL abbiamo la seguente struttura:
Repeat
Istruzione1;
istruzione2;
istruzione3;
…..
istruzioneN
until condizione;
Osserviamo che:
 il ciclo inizia con la parola repeat non seguita dal punto e virgola;
 dopo la parola repeat deve essere inserita la sequenza di istruzioni da eseguire ciclicamente;
 al termine della sequenza si scrive la parola until seguita dalla condizione di cui deve essere
controllata la verità (tale condizione può essere espressa in forma di uguaglianza, variabile =
valore, oppure disuguaglianza, variabile > valore);
 l’ultima riga di istruzioni prima della parola until non termina col punto e virgola!
 Dopo la condizione si termina con il punto e virgola.
19
In conseguenza della sua struttura, il ciclo repeat … until… presenta alcune importanti
caratteristiche:
 La condizione di cui si controlla la verità è espressa mediante una variabile, che deve essere
dichiarata e deve essere inizializzata (ossia si deve assegnare un valore iniziale a tale
variabile); l’inizializzazione deve essere effettuata prima del ciclo.
 Poiché il controllo sul valore di verità della condizione avviene alla fine della sequenza di
istruzioni, tale sequenza viene eseguita sempre almeno una volta.
 All’interno della sequenza d’istruzioni deve comparire un’istruzione che modifica
opportunamente il valore della variabile di controllo, in modo che, prima o poi, la condizione di
controllo diventi vera e il programma esca dal ciclo (senza questa modifica il programma ripete
indefinitamente il ciclo e non ne esce mai, entra in un loop infinito).
Analizziamo un programma esempio che utilizza la struttura repeat…until…; questo programma
calcola il prodotto di due numeri naturali, a e b, mediante somme successive.
Per scrivere questo programma dobbiamo chiederci come eseguire un prodotto mediante somme
successive:
 Dobbiamo sommare il numero “a” con se stesso e immagazzinare il risultato parziale in una
variabile P;
 Dobbiamo sommare il risultato parziale P con “a”;
 Dobbiamo controllare se abbiamo sommato “a” con se stesso un numero di volte pari a “b”
 Dobbiamo ripetere i 2 passi precedenti sino ad aver eseguito un numero di somme pari a “b”.
Conseguentemente abbiamo bisogno una variabile, I, che “conti” il numero di somme effettuate e di
una condizione che confronti I con b.
program ciclo2;
{Questo programma calcola il prodotto di due numeri naturali}
var a,b,P,I; integer;
{P è la variabile “prodotto; I è la variabile di controllo!}
begin
writeln(‘Inserisci il numero a’);
readln(a);
writeln(‘Inserisci il numero b’);
readln(b);
P:=0;
{la variabile P conterrà il prodotto e deve essere inizializzata a 0}
I:=0;
{la variabile I serve per “contare” il numero di passi}
Repeat
{notare l’assenza di BEGIN}
P:=a+P;
{si somma a P il valore di a, al primo passo P da 0 diventa a}
I:=I+1
{incremento il “contatore” I; conto quante somme ho fatto}
until I = b;
{controllo I, finchè I<b si ripete il ciclo; quando I = b, finisce}
writeln(‘Il prodotto di ‘,a,’ per ‘,b,’ è ‘,P);
readln
end.
Supponiamo a = 4, b = 3:
20
prima del ciclo
P vale 0, I vale 0
passo 1
Assegna a P il valore P+a  P=0+4 P=4
Passo 2
Assegna a I il valore I+1  I=0+1 I=1 (prima somma)
Passo 3
Controlla se I = 3 (FALSO  prosegue)
Passo 4
Assegna a P il valore P+a  P=4+4 P=8
Passo 5
Assegna a I il valore I+1  I=1+1 I=2 (seconda somma)
Passo 6
Controlla se I = 3 (FALSO  prosegue)
Passo 7
Assegna a P il valore P+a  P=8+4 P=12
Passo 8
Assegna a I il valore I+1  I=2+1 I=3 (terza somma)
Passo 9
Controlla se I = 3 (VERO  esce)
Il valore ottenuto per P è 12 e tale numero viene scritto in output
Nota: appare evidente che è necessario prestare molta attenzione nel formulare la condizione di
uscita dal ciclo.
Esercizi
1. Scrivi un programma che, letti due numeri naturali, “a” e “b”, con a > b, da tastiera, calcoli
il quoziente intero e il resto della divisione mediante sottrazioni successive.
2. Scrivi un programma che, letto un numero naturale “n” da tastiera, calcoli la somma dei
primi “n” numeri dispari.
3.3.3
Il ciclo WHILE …DO…
Un secondo tipo di struttura utilizzabile quando non si conosce a priori il numero di iterazioni è il
costrutto while…do…
Il ciclo while…do… (mentre…fai…) consente di ripetere una sequenza di istruzioni sino al
momento in cui una data condizione non diventa falsa (cioè fintantoché rimane vera). Nel ciclo
while…do… il controllo sulla verità è effettuato all’inizio della sequenza di istruzioni.
21
La struttura può essere rappresentata mediante il seguente diagramma di flusso:
condizione
falsa
vera
Istruzione 1
Istruzione 2
Istruzione n
In PASCAL abbiamo la seguente struttura:
while condizione do
begin
Istruzione1;
istruzione2;
istruzione3;
…..
istruzioneN
end;
Osserviamo che:
 il ciclo inizia con la parola while seguita dalla condizione di controllo e dalla parola do;
 la sequenza di istruzioni da eseguire ciclicamente è racchiusa fra le parole begin e end; (col
punto e virgola);
 la condizione di controllo è esaminata subito, prima di eseguire il blocco d’istruzioni (tale
condizione può essere espressa in forma di uguaglianza, variabile = valore, oppure
disuguaglianza, variabile > valore);
 l’ultima riga di istruzioni prima della parola end non termina col punto e virgola!
In conseguenza della sua struttura, il ciclo while … do… presenta alcune importanti caratteristiche:
 La condizione di cui si controlla la verità è espressa mediante una variabile, che deve essere
dichiarata e deve essere inizializzata (ossia si deve assegnare un valore iniziale a tale
variabile); l’inizializzazione deve essere effettuata prima del ciclo.
 Poiché il controllo sul valore di verità della condizione avviene all’inizio della sequenza di
istruzioni,. se la condizione è falsa al primo controllo la sequenza d’istruzioni non viene
eseguita.
 All’interno della sequenza d’istruzioni deve comparire un’istruzione che modifica
opportunamente il valore della variabile di controllo, in modo che, prima o poi, la condizione di
controllo diventi falsa e il programma esca dal ciclo (senza questa modifica il programma ripete
indefinitamente il ciclo e non ne esce mai, entra in un loop infinito).
22
Analizziamo un programma esempio che utilizza la struttura while…do…; questo programma
calcola il massimo comun divisore di due numeri naturali, a e b, mediante sottrazioni successive.
program MCD;
{Questo programma calcola massimo comun divisore di due numeri naturali}
var a,b,temp, MCD,N1,N2; integer;
begin
writeln(‘Inserisci il numero a>0’);
readln(a);
writeln(‘Inserisci il numero b>0’);
readln(b);
N1:=a;
{N1 e N2 servono per “ricordare” i valori iniziali}
N2:=b;
while a<>b do
{il simbolo <> significa “diverso da”}
if a>b then a:= a-b;
{se a>b si sottrae b da a e si mette il risultato in a}
else b:=b-a;
{se b>a si sottrae a da b e si mette il risultato in b}
MCD:=a;
writeln(‘Il MCD di ’, N1,’e ‘,N2,’ è ‘,MCD);
readln
end.
Supponiamo a = 24, b = 9:
Prima del ciclo
a=24
b=9
passo 1
Controlla se a≠b, se a=b va a fine ciclo direttamente, il MCD è proprio a
Passo 2
Controlla se a>b (VERO)a=24 - 9= 15,
Passo 3
Controlla se a≠b (VERO)
Passo 4
Controlla se a>b (VERO)a=15 - 9= 6,
Passo 5
Controlla se a≠b (VERO)
Passo 6
Controlla se a>b (FALSO)B=9 - 6= 3,
Passo 7
Controlla se a≠b (VERO)
Passo 8
Controlla se a>b (VERO)a=6 - 3= 3,
Passo 9
Controlla se a≠b (FALSO) ESCE DAL CICLO
b = 6; ritorna a inizio ciclo
b = 9; ritorna a inizio ciclo
a = 6; ritorna a inizio ciclo
b = 3; ritorna a inizio ciclo
Il valore ottenuto per a (ora uguale a b) è 3, rappresenta il massimo divisore
comune e tale numero viene scritto in output
23
Nota: appare evidente che è necessario prestare molta attenzione nel formulare la condizione di
uscita dal ciclo.
4
Esercizi
4.1
Esercizi (senza utilizzo di selezione e cicli)
Scrivi dei programmi che risolvano questi problemi.
1. Inserire due numeri interi da tastiera (a, b), dividere il primo per il secondo e scrivere il
quoziente intero e il resto della divisione.
2. Leggere un numero intero, calcolare il successore.
3. Leggere un numero reale da tastiera, calcolare il reciproco.
4. Calcolare l’area di un triangolo, dati la base e l’altezza (numeri reali).
5. Calcolare l’area di un trapezio, dati le basi e l’altezza (numeri reali).
4.2
Esercizi (richiedono l’utilizzo della selezione)
Scrivi dei programmi che risolvano questi problemi.
1. Inserire due numeri interi da tastiera (a, b) riconoscere se a è divisibile per b e scrivere un
messaggio opportuno.
2. Inserire da tastiera 3 numeri (a, b, c), stabilire se a e b sono entrambi multipli di c.
3. Calcolare l’are di una delle seguenti tre figure, dopo aver fatto comparire sullo schermo un
menù che permetta di scegliere la figura voluta: a) rettangolo; b) triangolo; c) trapezio.
4. Inserire due frazioni e stabilire quale delle due è maggiore.
5. Leggere 3 numeri (a, b, c) e stamparli in ordine, dal più piccolo al più grande.
6. Leggere tre numeri e stamparli in ordine dal più grande al più piccolo.
4.3
Esercizi (richiedono l’uso dell’iterazione)
Scrivi dei programmi che risolvano questi problemi.
1. Addizionare i primi 10 numeri dispari.
2. Addizionare i primi 10 multipli di 3.
3. Leggere n numeri da tastiera e determinarne il più piccolo.
4. Leggere un numero da tastiera e determinarne tutti i divisori.
4.4
Problemi vari (richiedono l’uso dell’iterazione e/ selezione)
Scrivi dei programmi che risolvano questi problemi.
1. .
24