Corso di Laurea in Scienze Ambientali – Corso di Fisica Generale II – a.a. 2010/11
Prova Parziale del 9/5/2011 - NOME____________________________________
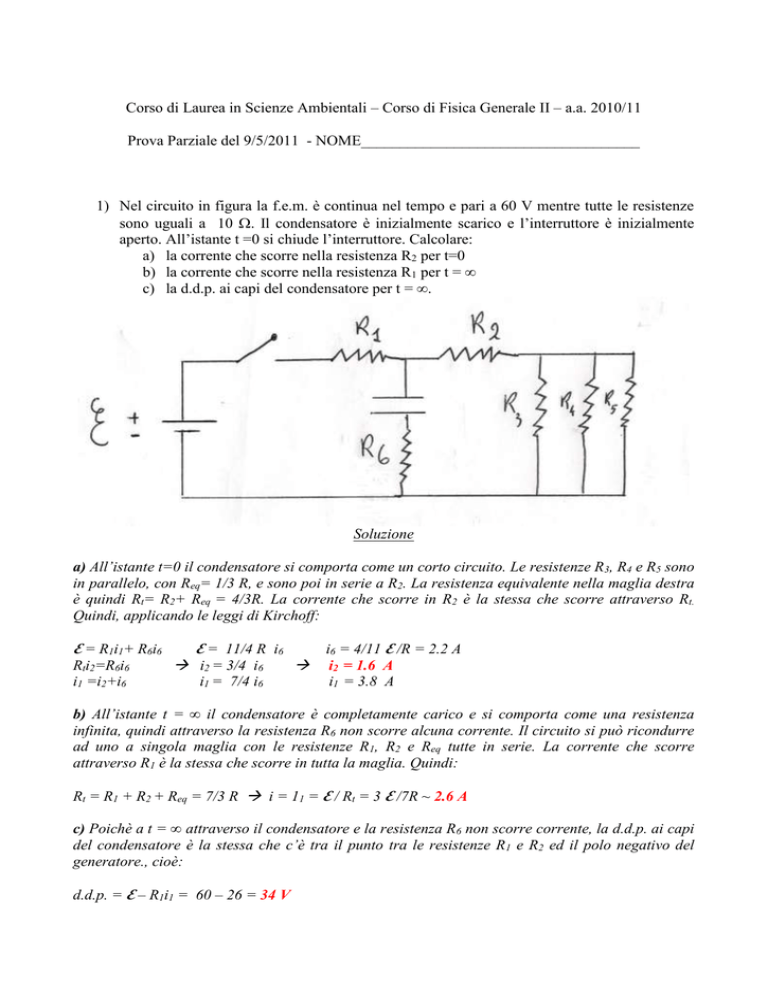
1) Nel circuito in figura la f.e.m. è continua nel tempo e pari a 60 V mentre tutte le resistenze
sono uguali a 10 . Il condensatore è inizialmente scarico e l’interruttore è inizialmente
aperto. All’istante t =0 si chiude l’interruttore. Calcolare:
a) la corrente che scorre nella resistenza R2 per t=0
b) la corrente che scorre nella resistenza R1 per t = ∞
c) la d.d.p. ai capi del condensatore per t = ∞.
Soluzione
a) All’istante t=0 il condensatore si comporta come un corto circuito. Le resistenze R3, R4 e R5 sono
in parallelo, con Req= 1/3 R, e sono poi in serie a R2. La resistenza equivalente nella maglia destra
è quindi Rt= R2+ Req = 4/3R. La corrente che scorre in R2 è la stessa che scorre attraverso Rt.
Quindi, applicando le leggi di Kirchoff:
E = R1i1+ R6i6
Rti2=R6i6
i1 =i2+i6
E = 11/4 R i6
i2 = 3/4 i6
i1 = 7/4 i6
i6 = 4/11 E /R = 2.2 A
i2 = 1.6 A
i1 = 3.8 A
b) All’istante t = ∞ il condensatore è completamente carico e si comporta come una resistenza
infinita, quindi attraverso la resistenza R6 non scorre alcuna corrente. Il circuito si può ricondurre
ad uno a singola maglia con le resistenze R1, R2 e Req tutte in serie. La corrente che scorre
attraverso R1 è la stessa che scorre in tutta la maglia. Quindi:
Rt = R1 + R2 + Req = 7/3 R i = 11 = E / Rt = 3 E /7R ~ 2.6 A
c) Poichè a t = ∞ attraverso il condensatore e la resistenza R6 non scorre corrente, la d.d.p. ai capi
del condensatore è la stessa che c’è tra il punto tra le resistenze R1 e R2 ed il polo negativo del
generatore., cioè:
d.d.p. = E – R1i1 = 60 – 26 = 34 V
2) Due sfere concentriche, cariche e in vuoto, hanno raggio 10 cm e 20 cm. La carica sulla
sfera interna è di 50 pC/cm2 mentre sulla sfera esterna la carica è di 20 pC/cm2. Calcolare il
modulo del campo elettrico alla distanza di 15 e 25 cm dal centro della sfera più interna.
Inoltre: se una carica elettrica si trova ad una distanza di 100 m dal centro delle due sfere
qual è il suo potenziale elettrico (assumendo V=0 all’infinito. Memo: 0 = 8.85 10-12 nel SI).
La risposta ai primi due quesiti deriva dall’applicazione del teorema di Gauss. Il problema ha
simmetria sferica: il campo elettrico è diretto radicalmente con verso uscente dalle due sfere
cariche positivamente. Sulla sfera più interna la carica totale è = 50 10 -12 x 4 x 3.14 x 102 = 6.28
10-8 C e su quella esterna invece la carica è = 20 10-12 x 4 x 3.14 x 4 102 = 10-7 C.
a) Si considera ovviamente una superficie gaussiana sferica di raggio 15 cm. Il flusso di E
attraverso la superficie vale: E = E 4r0.28ed è anche uguale a q/0 dove la carica q è solo
quella presente sulla sfera più interna. Quindi E = 6.28 10-8 / (0.28 x 8.85 10-12) = 2.5 104V/m
b) Si procede come per il punto a) ma la superficie gaussiana racchiude ora entrambe le
sfere e la carica da considerare è quella totale depositata sulle due sfere e cioè 1.63 10-11 C.
Si ha E = E 4r0.78 e quindi E = 1.63 10-7 / ( 0.78 x 8.85 10-12) = 2.4 104V/m
c) Per calcolare V occorre integrare il campo elettrico lungo un qualunque percorso dalla
distanza infinita fino al punto dove si trova la carica. Considerata la simmetria sferica del
problema conviene scegliere un cammino di integrazione lungo un raggio. Il campo elettrico è
quello prodotto da una carica puntiforme q = 1.63 10-7 C:
r
q
r
1
q
V (r ) E ds
dr
2
40 r
40
Quindi: V (100) = 1.63 10-7 x 8.99 109 x 10-2 = 14.7 V
r
q
1
r
40 r
QUESITI
1) Una stufetta elettrica viene usata per mantenere costante la temperatura di una stanza che
disperde verso l’esterno 400 J/s. Se la resistenza della stufetta è di 100 quale d.d.p. dovrà
essere applicata?:
4V
4 104 V
■
200 V
2 104 V
2) Due condensatori, rispettivamente con C1 = 10 F e C2 = 30 pF, sono collegati in serie. Qual
è il valore approssimativo della capacità equivalente?
10.00003 F
10 F
5 F
■
30 pF
3) Su una piastra metallica le cariche elettriche come si dispongono?
■ su entrambe le facce
in tutto il volume
su una delle due facce
non è possibile rispondere
4) Un elettrone con una energia potenziale elettrica di 1 eV a quale potenziale si trova?
■ 1V
1.602 10-19 V
6.242 10+18 V
dipende dalla distanza dalla sorgente del campo elettrico
5) Due lampadine con filamenti in filo di tungsteno di lunghezza identica con collegate ad uno
stesso generatore di f.e.m.: se la prima emette W1=100W di energia sotto forma di luce e la
seconda W2 =60 W in che rapporto stanno le sezioni dei due filamenti ?
s1/s2 = 36
s1/s2 = 0.028
■
s1/s2 = 1.67
s1/s2 = 0.17
6) Un amperometro con resistenza interna di 0.1 si utilizza per misurar la corrente continua
che scorre in un circuito a singola maglia dove è presente una resistenza di 10 Di quanto
differisce il valore misurato dall’intensità di corrente che scorre nel circuito senza
amperometro?
0.1 A
0.01%
le due correnti sono uguali
■
1%
7) L’energia immagazzinata in un condensatore a facce piane e parallele è di 2 mJ. Se la
capacità è di 1 nF e la distanza tra le armature è di 10 cm, qual è l’intensità del campo
elettrico all’interno del condensatore?
■ 20000 N/C
2 N/C
5 10-5 N/C
5 10-1 N/C
8) Un dipolo elettrico di momento p = 0.1 C.m è posto in un campo elettrico uniforme di
modulo pari a 10 N/C. Se viene fatto ruotare di 30 gradi, partire da un angolo di 90 gradi, di
quanto varia in modulo la sua energia potenziale?
0.5 J
dipende dall’angolo di partenza
■
0.87 J
0.71 J
9) La forza elettromotrice è definita come”
la forza esercitata dal generatore su ciascuna carica
la potenza dissipata dal generatore
■
Il lavoro svolto dal generatore per unità di carica
la d.d.p. presente ai capi del generatore
10) Una resistenza di 10 per effetto della corrente elettrica che la attraversa, si scalda di 100
Celsius ed il suo valore aumenta del 30%. Quanto vale il coefficiente termico di resistività
del materiale di cui è composta la resistenza trascurando le variazioni di volume?
3 K-1
0.3 K-1
■
0.003 K-1
30 K-1
11) Due cariche elettriche, rispettivamente parti a q1= – 9q e q2 = - 4q sono poste ad una
distanza d l’una dall’altra. A quale distanza (sulla congiungente di q1 e q2) dalle due cariche
deve essere posta una terza carica, q3, positiva, perché tutte e tre le cariche restino
immobili?
ad una distanza (4/9)d dalla carica q1
ad una distanza (9/25)d dalla carica q1
ad una distanza (2/5)d dalla carica q1
■
ad una distanza (3/5)d dalla carica q1
12) Una carica elettrica segue una traiettoria circolare, complessivamente lunga 1 m, sollecitato
unicamente da un campo elettrostatico di modulo pari a 10 N/C. Dopo 10 giri completi di
quanto è variata la sua energia potenziale?
U = 100 J
non si può rispondere senza conoscere direzione e verso del campo elettrico
■
non è variata
U = 10 J












