3. Il diodo a giunzione
3.1 La giunzione pn
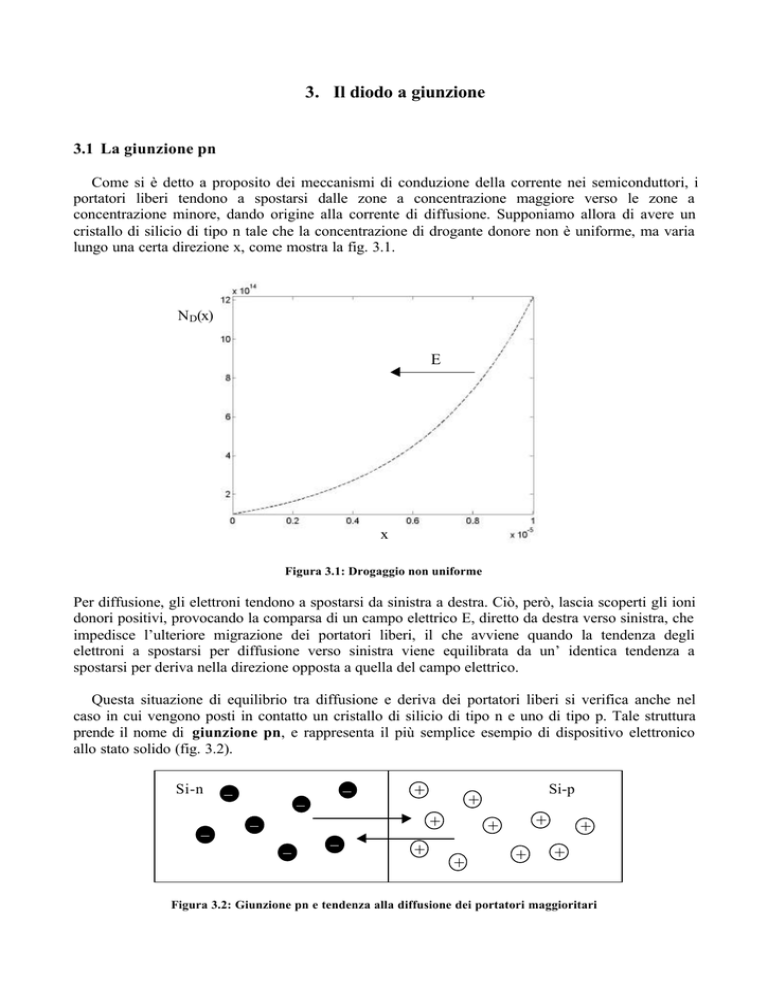
Come si è detto a proposito dei meccanismi di conduzione della corrente nei semiconduttori, i
portatori liberi tendono a spostarsi dalle zone a concentrazione maggiore verso le zone a
concentrazione minore, dando origine alla corrente di diffusione. Supponiamo allora di avere un
cristallo di silicio di tipo n tale che la concentrazione di drogante donore non è uniforme, ma varia
lungo una certa direzione x, come mostra la fig. 3.1.
ND(x)
E
x
Figura 3.1: Drogaggio non uniforme
Per diffusione, gli elettroni tendono a spostarsi da sinistra a destra. Ciò, però, lascia scoperti gli ioni
donori positivi, provocando la comparsa di un campo elettrico E, diretto da destra verso sinistra, che
impedisce l’ulteriore migrazione dei portatori liberi, il che avviene quando la tendenza degli
elettroni a spostarsi per diffusione verso sinistra viene equilibrata da un’ identica tendenza a
spostarsi per deriva nella direzione opposta a quella del campo elettrico.
Questa situazione di equilibrio tra diffusione e deriva dei portatori liberi si verifica anche nel
caso in cui vengono posti in contatto un cristallo di silicio di tipo n e uno di tipo p. Tale struttura
prende il nome di giunzione pn, e rappresenta il più semplice esempio di dispositivo elettronico
allo stato solido (fig. 3.2).
Si-n
_
_
_
_
+
_
+
_
_
+
Si-p
+
+
+
+
+
+
+
Figura 3.2: Giunzione pn e tendenza alla diffusione dei portatori maggioritari
Come si indica in figura, gli elettroni tendono a passare nella regione in cui essi sono minoritari,
per diffusione, così come le lacune si spostano verso la regione di tipo n, per lo stesso fenomeno.
Questa migrazione di portatori liberi lascia scoperta una certa quantità di ioni positivi donori nella
regione n e altrettanti ioni negativi accettori nella regione p, come visualizzato in fig. 3.3.
regione di carica spaziale
Si-n
_
+
_
+
_
_
Si-p
+
_
+
ioni donori
+
+
+
+
+
+
+
ioni accettori
E
Figura 3.3: Giunzione pn all’equilibrio e formazione della regione di carica spaziale
La regione a ridosso della giunzione, ormai svuotata di portatori liberi, si chiama appunto
regione di svuotamento o regione di carica spaziale. All’equilibrio, la sua estensione nelle due
regioni di semiconduttore drogate in modo diverso dipende dai relativi livelli di drogaggio ND e NA,
Infatti, affinché sia assicurata la neutralità elettrica dell’intera struttura (la carica totale netta
contenuta deve essere nulla), la regione di carica spaziale si estenderà di più nella regione di
semiconduttore caratterizzata da concentrazione inferiore di drogante.
All’interno della regione di carica spaziale esiste ovviamente un campo elettrico E, a causa della
presenza delle cariche fisse. Tale campo elettrico si oppone alla diffusione dei portatori liberi, per
cui si raggiunge un equilibrio tra diffusione e deriva dei portatori stessi.
Esiste quindi anche una differenza di potenziale che si localizza ai capi della struttura. Se però
chiudiamo un circuito elettrico con un conduttore, come indicato in fig. 3.4, non otteniamo alcuna
corrente, in quanto alle giunzioni tra il semiconduttore e il metallo usato come conduttore, in modo
del tutto analogo a quanto descritto per la giunzione pn, si formano delle regioni di svuotamento e
delle cadute di potenziale (potenziali di contatto) che inibiscono il passaggio di una corrente.
Si-n
_
+
_
_
_
_
+
+
+
+
+
+
Si-p
+
+
+
+
ID=0
Figura 3.4: Giunzione pn cortocircuitata
La giunzione pn è in pratica un diodo allo stato solido. Si tratta di un elemento a due terminali e
il suo simbolo circuitale è mostrato nella figura 3.5, assieme alle convenzioni di segno che verranno
adottate nel seguito per la tensione e la corrente nel dispositivo. Il catodo corrisponde alla regione
di tipo n, mentre l’anodo corrisponde alla zona drogata di tipo p.
-
+
VD
anodo
(Si-p)
catodo
(Si-n)
ID
Figura 3.5: Diodo a giunzione: simbolo circuitale e convenzioni di segno
3.2 La giunzione pn in polarizzazione inversa
Quando la tensione ai capi della giunzione pn è negativa, secondo la convenzione definita in fig.
3.5, allora si dice che la giunzione è polarizzata inversamente. In pratica, quindi, si ha
polarizzazione inversa se VD<0, come in fig. 3.6.
_
VD
+
E
Figura 3.6: Diodo polarizzato inversamente
A causa della polarizzazione imposta alla struttura, gli elettroni vicini al bordo della regione di
carica spaziale nella regione di tipo n tendono a spostarsi verso l’esterno della struttura, lasciando
quindi scoperti ulteriori ioni donori fissi. Anche le lacune vicine al bordo della regione di
svuotamento nella zona drogata di tipo p tendono ad allontanarsi dalla giunzione, per cui altri ioni
fissi accettori restano scoperti. L’effetto risultante è un allargamento della regione di carica
spaziale, come viene illustrato nella fig. 3.7.
regione di carica spaziale
Si-n
_
_
_
_
_
+ + +
+
+ + +
+ + +
Si-p
+ +
+
+ + +
IS
+
+
+
E
+
_
Figura 3.7: Polarizzazione inversa: allargamento della regione di carica spaziale
La corrente nella struttura è molto debole, in quanto le cariche libere disponibili per la
conduzione sono solo i portatori minoritari nelle rispettive regioni, in concentrazione estremamente
limitata. Tali portatori generano quindi una piccolissima corrente inversa IS, che scorre dal catodo
verso l’anodo (vedi fig. 3.7) e risulta quasi indipendente dalla tensione inversa applicata. I valori
tipici di IS dipendono molto dall’area e dai livelli di drogaggio del diodo e possono andare da 10-10 a
10-16 [A].
Poiché la concentrazione di portatori minoritari aumenta con la temperatura, la corrente IS, detta
anche corrente di saturazione inversa del diodo, aumenta con la temperatura.
Il fenomeno del breakdown
Se si aumenta la tensione inversa applicata al diodo, in corrispondenza di un certo valore si
verifica il fenomeno del breakdown del diodo, che consiste in un aumento notevolissimo della
corrente inversa che scorre nel diodo rispetto al valore I S della corrente di saturazione inversa, come
illustrato in fig. 3.8. Tale valore di tensione VZ viene detto appunto tensione di breakdown del
diodo.
ID
-VZ
VD
Figura 3.8: Breakdown di una giunzione pn polarizzata in inversa
La fig. 3.8 in realtà non rispetta fedelmente gli ordini di grandezza delle correnti in gioco: in una
scala realistica la corrente di saturazione inversa I S non è visibile, in quanto praticamente
sovrapposta all’asse delle tensioni. Si noti che, nella regione di breakdown, il diodo si comporta in
pratica come un generatore di tensione, in quanto tende a mantenere una tensione inversa costante
VZ ai suoi capi per qualunque valore di corrente inversa.
Vi sono due effetti fisici differenti che innescano il fenomeno del breakdown in un diodo.
a) L’effetto zener è dovuto all’aumento del campo elettrico nella regione di carica spaziale,
che si verifica specialmente nel caso di elevati livelli di drogaggio. Quando si giunge alla
tensione di breakdown, il campo elettrico diventa così intenso da causare la rottura di un
gran numero di legami covalenti, con la conseguente generazione di moltissime coppie
elettrone-lacuna. Ciò porta quindi a un brusco aumento delle corrente inversa. I diodi per i
quali il breakdown si verifica a causa dell’effetto zener presentano una tensione di
breakdown non superiore a 5-6V. Inoltre, per questi diodi un aumento della temperatura
provoca una diminuzione della tensione di breakdown VZ.
b) L’effetto valanga si verifica invece quando dei portatori liberi nella regione di carica
spaziale, che, come detto prima sono in numero molto limitato in condizioni normali,
acquisiscono una notevole quantità di energia cinetica. Se uno di questi portatori
interagisce con il reticolo cristallino, l’urto può provocare la generazione di una coppia di
portatori liberi, che, a loro volta, acquisendo l’energia cinetica necessaria e cedendola al
reticolo, possono crearne un’altra, innescando un processo di moltiplicazione a valanga dei
portatori liberi. Il risultato è il breakdown del diodo, cioè l’aumento repentino della
corrente inversa. I diodi per i quali il fenomeno del breakdown è associato all’effetto
valanga hanno tensioni di breakdown maggiori di 6-7V e in questo caso il coefficiente di
temperatura di VZ è positivo, cioè la tensione di breakdown aumenta con la temperatura.
C’è da sottolineare che il breakdown di una giunzione pn non è necessariamente un fenomeno
distruttivo . Se si limita in qualche modo l’aumento di corrente inversa e si impedisce quindi che la
potenza da dissipare superi il limite tollerabile dal diodo, esso può lavorare stabilimente in un punto
operativo all’interno della regione di breakdown.
Effetti capacitivi associati a un diodo polarizzato inversamente
Abbiamo visto che la carica fissa contenuta nella regione di svuotamento di un diodo polarizzato
inversamente varia al variare della tensione inversa applicata VR=-VD. Esiste quindi una funzione
QS(V R) che descrive appunto la dipendenza di tale carica QS dalla tensione applicata al diodo e che
è fortemente non lineare, come si vede in fig. 3.9.
QS
VR=-VD
Figura 3.9: Carica nella regione di svuotamento in funzione della tensione inversa VR =-VD
Una variazione di tensione inversa nel tempo richiede quindi una variazione della quantità di
carica QS nel tempo, che causa un transitorio nella corrente inversa, necessario per fornire la
differenza di carica richiesta. In definitiva si ha un effetto capacitivo, che però è di tipo non lineare,
in quanto la caratteristica carica-tensione Q S(VR) non è una retta passante per l’origine.
Se però il diodo viene fatto lavorare in un certo punto di lavoro Q, sempre in polarizzazione
inversa, e si considerano spostamenti abbastanza piccoli intorno al punto di lavoro, la caratteristica
QS(VD) può essere linearizzata intorno a tale punto, cioè la caratteristica non lineare può essere
confusa con la sua tangente nel punto di lavoro. Di conseguenza si può definire una capacità di
piccolo segnale del diodo polarizzato in inversa, come derivata della funzione QS(VR ) rispetto a VR,
calcolata nel punto di lavoro Q, come illustrato dalla fig. 3.10.
Tale capacità prende il nome di capacità di transizione :
CT =
dQS
dVR
Q
QS
CT =
QS
dQS
dVR
Q
Q
punto di lavoro Q
Q
VR
VR
Figura 3.10: Capacità di transizione CT.
3.3 La giunzione pn in polarizzazione diretta
Quando la tensione ai capi della giunzione pn è positiva, secondo le convenzioni di segno che
abbiamo scelto (fig. 3.5), si dice che il diodo è polarizzato direttamente. Quindi un diodo è
polarizzato direttamente se VD>0, come in fig. 3.11.
_
VD
+
E
Figura 3.11: Diodo polarizzato direttamente
In questo caso, rispetto alla condizione di equilibrio, corrispondente a VD=0, l’estensione della
regione di carica spaziale diminuisce, in quanto la polarizzazione applicata tende a favorire il
passaggio dei portatori liberi dalla regione in cui sono maggioritari, verso quella in cui sono
minoritari. Di conseguenza gli ioni vicini al bordo della regione di carica spaziale possono
riacquistare la carica che avevano perduto e diventano atomi neutri, per cui la regione di carica
spaziale si restringe. Ciò implica che la differenza di potenziale ai capi della regione di
svuotamento, che all’equilibrio (VD=0) impediva la migrazione libera dei portatori maggioritari, si
riduce notevolmente e quindi non è più in grado di controbilanciare la tendenza alla diffusione dei
portatori maggioritari stessi. Il risultato è che si produce un flusso di elettroni che si spostano per
diffusione dalla regione di tipo n a quella di tipo p e un flusso di lacune che si spostano nel verso
opposto, dando luogo a due contributi di corrente nello stesso verso, che è quello definito positivo
dalla nostra convenzione. Il fenomeno è illustrato nella seguente fig. 3.12.
regione di carica spaziale
Si-n
_
_
_
+
+
+
+
+
_
_
+
+
_
E
_
Si-p
+
+
_
+
+
+
+
ID
+
Figura 3.12: Polarizzazione diretta: riduzione della regione di carica spaziale e corrente diretta
La corrente in un diodo polarizzato direttamente è, quindi, una corrente di diffusione e cresce
molto rapidamente con la polarizzazione diretta applicata. La relazione ID(VD) è infatti di tipo
esponenziale, descritta dalla seguente equazione (3.1),
VD
nV
I D = IS e T −1
(3.1)
in cui abbiamo:
n = coefficiente di emissione, adimensionale, di valore tipico compreso tra 1 e 2;
kT
VT = tensione termica, pari a
, essendo k la costante di Boltzmann, T la temperatura assoluta
q
e q la carica dell’elettrone;
IS è sempre la corrente di saturazione inversa.
Il valore della tensione termica a temperatura ambiente è di circa 25mV. In quasi tutti i casi pratici
in cui il diodo è acceso, si può trascurare l’unità rispetto al termine esponenziale, il che significa che
ID>>IS. Quindi:
VD
I D ≅ IS e
(3.2)
La seguente fig. 3.13 mostra la tipica caratteristica di un diodo, in cui la corrente si può
considerare praticamente trascurabile fino a VD=Vγ ≈ 0.5V (spesso considerato come il valore della
tensione di soglia del diodo). Inoltre la tensione ai capi del diodo non varia molto quando è ben
acceso, a causa della caratteristica esponenziale (3.2), e il suo valore si aggira sempre intorno a
0.6÷0.8V, tipicamente 0.7V.
nVT
ID
Vγ
VD
Figura 3.13: Caratteristica esponenziale di un diodo in diretta
Effetti capacitivi associati a un diodo polarizzato direttamente
Anche nel caso di giunzione polarizzata direttamente si hanno degli effetti capacitivi, associati
questa vota all’accumulo dei portatori liberi iniettati dalla regione in cui sono maggioritari a quella
in cui sono minoritari. In altre parole, in corrispondenza di un certo valore di tensione diretta VD,
nelle regioni esterne alla regione di svuotamento (dette regioni quasi neutre) si è in presenza di un
eccesso di cariche minoritarie QD(VD), che varia al variare della polarizzazione, anche qui in modo
non lineare. Si può quindi definire, anche in questo caso, una capacità di piccolo segnale associata
al diodo polarizzato in diretta come la derivata della carica QD in funzione di VD, calcolata nel
punto di lavoro:
dQ D
CD =
dVD Q
Questa capacità viene denominata capacità di diffusione e tipicamente è di circa un ordine di
grandezza maggiore rispetto alla capacità di transizione.
Effetti della variazione della temperatura sulla caratteristica del diodo in diretta
Considerando l’eq. (3.2), che esprime la caratteristica di un diodo in diretta, si possono
riconoscere due effetti contrapposti della variazione della temperatura. Come sappiamo, la corrente
di saturazione inversa I S aumenta con la temperatura, per cui ID tende ad aumentare con essa. Anche
la tensione termica VT aumenta con la temperatura, provocando una tendenza alla diminuzione di ID
con T. L’effetto netto risultante di un aumento della temperatura è un aumento della corrente ID,
che si può quantificare come segue. Polarizzando il diodo a corrente costante, un incremento di un
grado della temperatura assoluta corrisponde a una diminuzione di 2mV della tensione VD ai capi
del diodo, come illustrato in fig. 3.14.
ID
T2
T1
ID=cost
∆VD
∆T
VD
= −2 mV / °C
ID =cos t
∆VD
Figura 3.14: Dipendenza della caratteristica del diodo in diretta dalla temperatura
3.4 Punto di lavoro di circuiti a diodo
Consideriamo il circuito rappresentato in fig. 3.15, costituito da un generatore indipendente di
tensione, da un resistore lineare e da un diodo, caratterizzato dai parametri I S e n.
R
E
+
I
IS
n
_
V
Figura 3.15: Semplice circuito a diodo
Per determinare il punto di lavoro del circuito, cioè per determinare il valore delle grandezze
elettriche del circuito (con particolare riferimento alla tensione V e alla corrente I associate al
diodo), bisogna risolvere il seguente sistema di equazioni, ottenuto a partire dalle caratteristiche
degli elementi del circuito e dalle leggi di Kirchoff:
V
I = I e nVT
S
E = V + RI
a)
(3.3)
b)
Questo sistema non si può risolvere analiticamente in forma chiusa, per cui possiamo, per
esempio, usare un approccio grafico. Nel piano V-I dobbiamo riportare la caratteristica del diodo e
la caratteristica della restante parte del circuito, cioè della serie generatore di tensione-resistenza.
Quest’ultima caratteristica è ovviamente rappresentata da una retta, che è facilmente tracciabile
considerando che passa per i punti (E,0) e (0, ISC ). Tali punti rappresentano le intercette della retta
rispettivamente con l’asse delle tensioni e con l’asse delle correnti, cioè la tensione a vuoto e la
corrente di corto-circuito del bipolo costituito dalla serie generatore-resistenza.
Il punto di lavoro del circuito sarà individuato dall’intersezione tra le due caratteristiche, come
viene visualizzato in fig. 3.16.
I
I SC =
E
R
IQ
retta di carico
Q
VQ
E
Figura 3.16: Determinazione del punto di lavoro con metodo grafico
V
La retta che rappresenta la caratteristica della serie generatore di tensione-resistenza viene
denominata retta di carico. Il concetto di retta di carico verrà ripreso spesso nel seguito, quando si
tratterà di determinare il punto di lavoro di circuiti contenenti elementi non lineari, come i
transistori.
Metodo numerico iterativo per la determinazione del punto di lavoro
Per risolvere il problema della determinazione del punto di lavoro del circuito in fig. 3.15, si può
usare anche un approccio di tipo numerico iterativo. La procedura inizia con una prima, grossolana
stima del valore della tensione V o della corrente I. Per esempio si può ipotizzare che il valore della
tensione ai capi del diodo nel punto di lavoro sarà non molto lontano da V0 =0.7V. A questo punto si
usa una delle due equazioni (3.3a) o (3.3b) per determinare una prima stima dell’altra variabile, nel
nostro caso la corrente I. Per esempio, si può usare la (3.3b) per determinare I0 :
E − V0
I0 =
R
Lo schema numerico continua con la determinazione di una nuova stima della prima variabile,
quella usata in partenza, nel nostro caso V1 , a partire da I0 . Per trovare questa stima si utilizza
questa volta l’equazione che non è stata ancora usata, nel nostro esempio la (3.3a), cioè l’equazione
del diodo:
I0
V1 = nVT ln
IS
A questo punto si continua a iterare, utilizzando alternativamente l’equazione (3.3b) per trovare
nuove stime della corrente I e l’equazione (3.3a) per determinare nuove approssimazioni della
tensione V. L’iterazione termina quando la differenza tra due stime successive è abbastanza piccola,
il che significa che l’errore che si commette sulla determinazione di una variabile è sufficientemente
piccolo.
A titolo di esempio, la seguente tabella riporta i successivi valori di tensione e di corrente che si
ottengono, sempre per il circuito in fig. 3.15, con i seguenti valori dei parametri:
E=6V, R=5kΩ, I S=10nA, n=2.
V 0 = 0.7
I0
=0.5786 V
IS
I'
V' ' = nVT ln =0.5797 V
IS
V' = nVT ln
E − V0
=1.06 mA
R
E − V'
I' =
=1.084 mA
R
I0 =
I' ' =
E − V' '
=1.084 mA
R
Come si può notare, con poche iterazioni si ottiene il valore del punto di lavoro con un numero di
cifre significative delle variabili abbastanza grande e inutile nella maggior parte delle applicazioni.
Metodi numerici di questo tipo, basati su un altro tipo di algoritmo (es. iterazione di NewtonRaphson) vengono utilizzati dai simulatori circuitali al calcolatore per risolvere i complessi
problemi di calcolo proposti dalle reti contenenti elementi non lineari.
3.5 Modelli semplificati del diodo a giunzione
Quando non è necessario conoscere il punto di lavoro di un circuito con accuratezza elevata, il
che accade in molte applicazioni pratiche, è possibile approssimare la caratteristica del diodo con un
modello approssimato che consente di semplificare i calcoli in modo notevole. Anziché usare
direttamente la caratteristica esponenziale, quindi, la si può approssimare con un modello lineare a
tratti, che analiticamente si può esprimere attraverso le seguenti equazioni:
I D = 0
I = VD - VD0
D
rd
VD ≤ VD0
VD > VD0
La caratteristica approssimata viene confrontata con quella reale nelle seguente fig. 3.17.
ID
VD0
VD
Figura 3.17: Approssimazione lineare a tratti della caratteristica del diodo
Dal punto si vista circuitale, questa approssimazione equivale a sostituire il diodo, quando è
acceso, con la serie di un generatore di tensione costante pari a VD0 e di un resistore di valore rd. Il
valore dei parametri VD0 e rd non è univoco: diverse scelte portano a una migliore o peggiore
approssimazione della caratteristica in tratti diversi. Ad esempio, se consideriamo l’esempio
numerico precedente e scegliamo VD0=0.6V e r d=46Ω, otteniamo:
+
R
E
rd
VD0
I=
E − VD 0 6 − 0.6
=
[mA ] = 1.07 mA
R + rd
5.046
V I
_
V=VD0+rdI=0.649V ,
che non sono valori molto distanti da quelli calcolati con il metodo numerico iterativo utilizzato
precedentemente.
Il modello lineare a tratti viene spesso indicato come modello a batteria e resistenza.
La resistenza equivalente del diodo rd, inserita per render conto del fatto che la caduta di tensione
ai capi del diodo varia con la corrente nel diodo stesso, è di valore molto piccolo, e spesso può
essere trascurata rispetto alle altre resistenze del circuito. Un modello approssimato ancora più
semplice è allora quello in cui il diodo acceso si comporta come un semplice generatore di tensione
di valore VD0, cioè il cosiddetto modello a batteria. In molti casi pratici un modello a batteria con
VD0 pari a circa 0.7 V è più che sufficiente per calcolare con buona approssimazione il punto di
lavoro di un circuito contenente uno o più diodi.
Nell’esempio numerico precedente, questo semplicissimo modello fornirebbe un valore di
corrente nel circuito pari a:
R
E
I=
VD0
E − VD 0 6 − 0.7
=
[mA ] = 1.06 mA ,
R
5
che è ancora un’ottima approssimazione del valore previsto dalla caratteristica esponenziale, cioè
1.084mA.
Nel caso in cui le tensioni in gioco nel circuito sono molto grandi rispetto alla caduta di tensione
sul diodo, è possibile spingere al limite questa approssimazione, trascurando la caduta VD0. In tal
caso il diodo in inversa corrisponde a un circuito aperto, come sempre, mentre il diodo in diretta è
rappresentato da un corto circuito: si parla di modello a diodo ideale, la cui caratteristica è
rappresentata nella seguente fig. 3.18.
ID
VD ≤ 0
I D > 0
ID = 0
VD = 0
VD
Figura 3.18: Diodo ideale
3.5 Il modello per piccoli segnali del diodo
Consideriamo la fig. 3.19. In essa abbiamo lo stesso circuito di fig. 3.15, con in più un
generatore di tensione sinusoidale vs(t)=VS sinωt, che provoca uno spostamento nel tempo della
retta di carico. Di conseguenza il punto di lavoro del circuito si sposta nel tempo, spazzolando un
tratto della caratteristica non lineare del diodo, come viene evidenziato nella fig. 3.19.
I
R
E/R
+
I(t)
E
D
V(t)
_
vs(t)=VSsinωt
E
V
VS
t
Figura 3.19: Spostamento del punto di lavoro del circuito nel tempo
In figura è anche rappresentata la forma d’onda della tensione V(t), che, pur essendo periodica e
avendo la stessa frequenza della sinusoide vs(t), non è sinusoidale, poiché la caratteristica del diodo
non è lineare.
In pratica il generatore di tensione costante fissa un punto di lavoro statico Q, corrispondente
all’intersezione della caratteristica del diodo con la retta individuata dai punti (0,E/R) e (E,0),
mentre l’applicazione della sinusoide, che rappresenta un segnale che varia nel tempo, sposta il
punto di lavoro del circuito lungo la caratteristica del diodo in un intorno di Q. La tensione V(t) e la
corrente I(t) sono dunque funzioni del tempo e possono essere pensate come somma di una
componente statica, cioè il valore che queste grandezze assumono nel punto di lavoro statico, e di
una variazione intorno a questo punto di lavoro statico. In pratica:
I(t)=IQ+∆I(t)
V(t)=VQ+∆V(t)
Le variazioni di corrente e di tensione ∆I(t) e ∆V(t) rispetto ai relativi valori statici IQ e VQ si
definiscono rispettivamente segnale di corrente e segnale di tensione. Nel seguito indicheremo
sempre le grandezze statiche, corrispondenti al punto di lavoro statico, con lettere maiuscole e i
segnali di tensione e di corrente, cioè le variazioni di tensione e corrente intorno al punto di lavoro,
con lettere minuscole. Di conseguenza avremo:
∆I(t)=i(t)
∆V(t)=v(t) ;
I(t)=IQ+i(t)
V(t)=VQ+v(t)
Sempre con riferimento alla fig. 3.19, notiamo che, se le variazioni della tensione e della corrente
nel diodo sono abbastanza piccole, cioè se abbiamo a che fare con piccoli segnali, la caratteristica
del diodo intorno al punto di lavoro statico (che da ora in poi chiameremo semplicemente punto di
lavoro), può essere confusa con la tangente alla caratteristica stessa nel punto di lavoro. Quindi, nei
riguardi delle variazioni intorno al punto di lavoro, il diodo si comporta in prima approssimazione
come un resistore lineare, il cui valore si può determinare considerando la pendenza della sua
caratteristica nel punto di lavoro. In definitiva, concludiamo che l’equivalente del diodo per i piccoli
segnali è una resistenza rd che si valuta come l’inverso della derivata della caratteristica ID(VD) del
diodo stesso calcolata nel punto di lavoro.
rd =
1
1
=
gd
dI D
dVD
gd =
dI D
dVD
Q
VD
nV
VD
d IS e T
nVT
IS e
I QD
=
=
=
dVD
nVT
nVT
Q
(3.4)
Q
La (3.4) indica che la conduttanza equivalente del diodo si calcola dividendo la corrente del
diodo nel punto di lavoro per nVT . In molti casi abbiamo n≅1, per cui si ha semplicemente
gd≅ID /VT .
Se, quindi, consideriamo il caso della fig. 3.19, lo studio dell’andamento nel tempo della
tensione sul diodo si può condurre in due fasi successive:
1)
Calcolo del punto di lavoro, eseguito lasciando agire solo i generatori indipendenti costanti
nel tempo, nel nostro caso il generatore di tensione E.
R
E
2)
+
IQ
VQ
_
Calcolo delle variazioni delle tensioni e delle correnti del circuito intorno al punto di
lavoro, eseguito utilizzando il circuito equivalente per piccolo segnale, in cui il diodo viene
sostituito con la sua resistenza differenziale e si passivano i generatori indipendenti di
tensione e di corrente, lasciando agire solo i segnali che variano nel tempo. Nel nostro caso
il circuito equivalente per piccoli segnali è il seguente:
R
+
i = ∆I
vS
rd
v = ∆V
_
Ogni grandezza elettrica del circuito sarà valutata quindi come somma del suo valore statico,
determinato nella prima fase, e della sua variazione, valutata nella seconda fase.












