Temi di termodinamica
Prova scritta del 12/04/1995
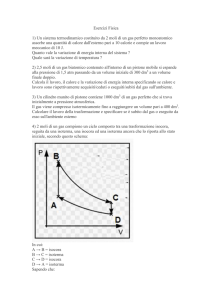
Una mole di gas perfetto monoatomico alla temperatura TA =243°K e pressione
pA = 2 atm, esegue un ciclo reversibile costituito dalle seguenti trasformazioni:
> espansione isobara AB;
> espansione adiabatica BC fino a pC = 1 atm, e TC=TA ;
> compressione isoterma CA fino a ritornare allo stato A.
Calcolare:
a) i parametri p,V,T di ogni stato e disegnare il ciclo in un piano (p,V);
b) il calore scambiato in ogni trasformazione;
c) il rendimento del ciclo
d) la variazione di entropia del gas lungo la trasformazione isoterma CA.
Soluzione: b) 1630J, 2020 J, 1400 J; c) 14%; d) –1.4 cal/°K
Prova scritta del 5/07/1995
Una mole di gas perfetto monoatomico alla temperatura TA=243°K e volume
VA= 10 litri, esegue un ciclo reversibile costituito dalle seguenti trasformazioni:
> espansione isobara AB fino a VB= 4 VA;
> trasformazione isocora BC fino a pC= 1/2 pA;
> compressione isobara CD fino a riportare il volume a VA;
> trasformazione isocora DA fino a ritornare allo stato A.
Calcolare:
a) i parametri p,V,T di ogni stato e disegnare il ciclo in un piano (p,V);
b) il lavoro compiuto dal gas;
c) il rendimento del ciclo;
d) la variazione di entalpia del gas lungo la trasformazione isocora DA.
Soluzione: b) 36.3 litri•atm; c) 19%; d) 24.9 litri•atm
Prova scritta del 3/04/1996
A)
Un gas perfetto monoatomico e' contenuto in un recipiente della capacita' di
10 litri alla temperatura di 27 °C e alla pressione di 4 atm. Calcolare:
a) il lavoro occorrente per comprimere isotermicamente e reversibilmente il gas fino
a un volume di 3 litri;
b) il lavoro ottenuto lasciando espandere il gas adiabaticamente e reversibilmente
fino al volume iniziale;
c) la variazione complessiva di entropia del gas in seguito alle trasformazioni
precedenti.
Soluzione: a) -48.2 litri•atm; b) 8.1 102 cal; c) –3.4 cal/°K
T1
B)
Un recipiente di volume 10 litri contiene 3 moli di un gas perfetto
monoatomico alla temperatura di 27 °C. Calcolare:
a) il lavoro occorrente per comprimere isotermicamente e reversibilmente il gas fino
a un volume di 3 litri;
b) il lavoro ottenuto lasciando espandere il gas adiabaticamente e reversibilmente
fino al volume iniziale;
c) la variazione complessiva di entropia del gas in seguito alle trasformazioni
precedenti.
Soluzione: a) –900 R ln0.3; b) Lgas = -Loccorrente; c) –3R ln(10/3)
Prova scritta del 4/07/1996
Una mole di gas perfetto monoatomico alla temperatura T0= 273 ºK e p0= 1 atm,
esegue un ciclo reversibile costituto da:
> un riscaldamento a pressione costante fino a V1 = 2V0
> un raffreddamento a volume costante fino ad una temperatura uguale a T0
> una compressione isoterma fino a ritornare allo stato iniziale.
a) Disegnare il ciclo nel piano p,V.
Calcolare:
a) il rendimento del ciclo;
b) la variazione di entropia del gas durante ciascuna delle tre trasformazioni.
Soluzione: b) 12%; c) 0.14 litri•atm/ °K, -0.09 litri•atm/ °K, -0.06 litri•atm/ °K
Prova scritta del 19/9/1996
Una massa di 1 kg di acqua a t1 = 20 °C viene raffreddata alla pressione atmosferica fino
ad ottenere ghiaccio a t2 = -20 °C. Calcolare:
a) la quantità di calore che e' stata sottratta;
b) la variazione di entropia del sistema acqua+ghiaccio.
Soluzione: a) –110 Kcal; b) –401.7 cal/°K
Prova scritta del 12/2/1997
A)
Due moli di gas perfetto monoatomico vengono portate da temperatura
T1 = 300 K a T2 = 3T1mediante una trasformazione adiabatica reversibile.
a) Determinare il rapporto V2/V1.
b) Quanto e' il lavoro compiuto durante il processo?
Soluzione: a) V2/V1 ≈ 0.19; b) L ≈ -15 KJ
2bis) Dimostrare l'espressione della variazione di entropia del gas perfetto.
T2
B)
Una mole di gas perfetto monoatomico viene portata dalla pressione p1 alla
pressione p2 = 3p1 mediante una isoterma reversibile a temperatura T1. Successivamente
mediante una adiabatica reversibile il gas viene riportato alla pressione p1.
a) Trovare la variazione di entropia del gas.
b) Quanto vale il rapporto tra la temperatura finale T2 e quella iniziale T1?
Soluzione: a)-9.1 J/°K ; b) T2/T1 ≈ 1.6
2bis) Il primo principio della termodinamica.
C) Una mole di gas perfetto monoatomico, a temperatura T1 = 300°K e pressione p1 = 1 atm,
viene portata, mediante una trasformazione adiabatica reversibile, alla temperatura T2 = 200°K.
Successivamente mediante un'isoterma reversibile il volume viene riportato al valore iniziale.
a) Quanto vale la pressione finale pf del gas?
b) Di quanto e' variata l'entropia del gas?
Soluzione: pf=0.67 atm ∆S= - 1.2 cal/°K
2bis) Propagazione del calore
Prova scritta del 27/3/1997
A)
Una certa quantità di acqua viene versata in un recipiente di volume V = 1 m3 tenuto
a pressione p = 1 atm e posto su un termostato a temperatura T = 373 °K in modo da
mantenere costante anche la temperatura. Si osserva che in tali condizioni tutta l'acqua
evapora e quindi va ad occupare l'intero volume del recipiente. Conoscendo il calore di
evaporazione λ = 539 cal/g e la densità dell'acqua liquida ρ = 1 g/cm3, trovare:
a) il numero di moli di H2O (si tratti il vapore acqueo come un gas perfetto di peso
molecolare M = 18);
b) la massa ed il volume dell'acqua;
c) la variazione di entropia del termostato a temperatura T.
Soluzione: a) n = 32.7; b) 588.5g, 588.5 cm3; c) -850 cal/°K
RECUPERO:
2bis) Il primo principio della termodinamica.
B)
Un recipiente di volume V = 2 m3 tenuto a pressione p =1 atm e mantenuto a
temperatura costante da un termostato a T = 373 °K, contiene acqua sotto forma di vapore. Il
volume viene ridotto, finche' esso contiene solo acqua liquida. Conoscendo il calore di
evaporazione λ = 539 cal/g e la densità dell'acqua liquida ρ = 1 g/cm3, trovare:
a) il numero di moli di H2O (si tratti il vapore acqueo come un gas perfetto di peso
molecolare M = 18);
b) la massa ed il volume di acqua quando tutto il vapore si e' liquefatto;
c) la variazione di entropia del vapore che si trasforma in acqua.
Soluzione: a) n = 65.4; b) 1177 g, 1.2 l; c) –1.7 Kcal/°K
T3
RECUPERO:
Lavoro in trasformazioni termodinamiche.
C)
Un litro di acqua viene versato in un recipiente tenuto a pressione p = 1 atm e
mantenuto a temperatura costante da un termostato a T = 373 °K. In tali condizioni tutta
l'acqua evapora e va ad occupare l'intero volume del recipiente. Conoscendo il calore di
evaporazione λ = 539 cal/g e la densità dell'acqua liquida ρ = 1 g/cm3, trovare:
a) la massa e il numero di moli di H2O (peso molecolare M = 18);
b) il volume del recipiente (si tratti il vapore acqueo come un gas perfetto);
c) la variazione di entropia dell'acqua.
Soluzione: a) m = 1 Kg, n = 55.6; b) 1.7 m3; c) 1.4 Kcal/°K
RECUPERO:
Dimostrare la relazione cp- cv = R per i gas perfetti
Prova scritta del 4/6/1997
A)
Un recipiente contiene m =1.2 g di idrogeno alla pressione p0 = 0.3 atm e
V0 = 32.8 litri. Al gas viene fatto eseguire un ciclo reversibile costituito da una espansione
adiabatica fino a un volume quadruplo di quello iniziale, da una isoterma fino a riprendere il
volume iniziale e da una isocora con la quale il ciclo si chiude.
Trattando l'idrogeno contenuto nel recipiente come un gas perfetto biatomico di peso
molecolare M=2:
a) disegnare il ciclo nel piano (p,V)
e calcolare:
b) la temperatura e la pressione del gas alla fine dell'adiabatica;
c) la variazione di entropia del gas durante la trasformazione isocora;
d) il lavoro compiuto dal gas durante la trasformazione isoterma.
Soluzione: a) 115 °K; b) 0.04 atm; c) 1.65 cal/°K; d) –7.84 litri•atm
B)
Una quantità' m =1.2 g di idrogeno, inizialmente a T1 = 115 °K e V1 = 131.2 l, e'
utilizzata per eseguire un ciclo reversibile costituito da una compressione isoterma fino a un
volume pari a 1/4 di quello iniziale, da una isocora fino a p3 e T3 e da una espansione
adiabatica fino a riprendere il volume iniziale con la quale il ciclo si chiude.
Trattando l'idrogeno contenuto nel recipiente come un gas perfetto biatomico di peso
molecolare M=2:
a) disegnare il ciclo nel piano (p,V)
e calcolare:
b) la temperatura e la pressione del gas all'inizio dell'adiabatica;
c) la variazione di entropia del gas durante la trasformazione isoterma;
d) il lavoro compiuto dal gas durante la trasformazione adiabatica.
Soluzione: a) 200 °K; b) 0.3 atm; c) –0.07 litri•atm/ °K; d) 10.5 litri•atm
T4
C)
Una quantità' pari a 0.6 moli di gas perfetto biatomico, inizialmente a p1 = 0.17 atm e V1
= 32.8 l, viene utilizzata per eseguire un ciclo reversibile costituito da una compressione
isocora fino a T2 = 200 °K, da una espansione adiabatica fino ad un volume V3 = 4 V2 e da una
isoterma fino a riprendere i valori iniziali con la quale il ciclo si chiude.
a) disegnare il ciclo nel piano (p,V) e calcolare:
b) la temperatura dell'isoterma e la pressione del gas all'inizio dell'isoterma;
c) la variazione di entropia del gas durante la trasformazione isoterma;
d) il calore scambiato durante la trasformazione isocora.
Soluzione: a) 113.3 °K; b) 0.04 atm; c) –0.07 litri•atm/ °K; d) 10.7 litri•atm
Prova scritta del 19/9/1997
Una resistenza, che sviluppa una potenza di 1500 watt, viene usata per scaldare 80 litri di
acqua da 15°C a 65°C.
a) Quanto calore viene fornito?
b) Quanto tempo occorre, supponendo che non vi siano dispersioni termiche?
c) Qual e' la variazione di entropia dell'acqua?
Soluzione: a) 4•103 Kcal; b) 3h 6m; c) 12.8 Kcal/°K
2a) Equazioni di Poisson per trasformazioni quasi-statiche di gas perfetti
2b) Gas perfetti e gas reali
Prova scritta parziale del 9/1/1998
1A) Una sbarra di ferro lunga L = 20 cm e sezione S = 3 cm2 ha un'estremità in un bagno
di acqua e ghiaccio a 0°C e l'altra in acqua bollente e vapore a 100°C. La conducibilità
termica della sbarra di ferro e' K= 0.16 cal/sec cm °K. Assumendo che il calore sia
trasmesso per conduzione solo attraverso la lunghezza della sbarra, si calcoli:
a) quanto calore viene trasmesso nell'unita' di tempo lungo la sbarra;
b) la quantità di calore trasferita dal vapore d'acqua al ghiaccio in 10 min;
c) la quantità di ghiaccio che fonde in 10 min;
d) la variazione di entropia dell'universo, nei 10 min
Soluzione: a) 2.4 cal/s; b) 1440 cal; c) 18 g; d) 1.4 cal/°K
2A) Due moli di gas perfetto monoatomico alla pressione e volume iniziali p1 = 6 atm,
V1 = 15 litri, compiono un ciclo reversibile costituito da:
1-2: espansione isoterma fino al volume V2 = 3V1;
2-3: decompressione isocora fino alla pressione p3;
3-1: compressione adiabatica fino allo stato iniziale.
Si chiede:
a) determinare le coordinate termodinamiche degli stati 1, 2, 3 e disegnare il ciclo;
b) determinare il lavoro complessivo compiuto dal gas durante il ciclo;
c) determinare il calore complessivo scambiato dal gas durante il ciclo;
d) determinare il rendimento del ciclo.
Soluzione: b) 2.9 KJ; c) 2.9 KJ ; d) 28.7%
T5
3A) Dimostrare la relazione cp – cv = R
4A) Disuguaglianza di Clausius e funzione di stato Entropia
1B) Una persona con metabolismo basale di 2000 Kcal/giorno, si trova in un sacco a
pelo di piumino (conducibilità termica K=0.006 cal/sec m °K) di superficie S=2 m2.
Considerando il corpo umano come un termostato a 37°C e che la temperatura della
superficie esterna del sacco a pelo sia 10°C, si calcoli:
a) lo spessore che deve avere il sacco a pelo, affinché il calore trasmesso per
conduzione attraverso la superficie del sacco a pelo sia proprio uguale a quello
del metabolismo basale della persona;
b) la quantità di calore che si trasmette per conduzione attraverso il sacco a pelo in 6
ore;
c) la variazione dell'entropia dell'universo nelle 6 ore.
Se la quantità di calore di cui al punto b) potesse essere usata per far evaporare dell'acqua
bollente, calcolare:
d) la quantità di vapore prodotto.
Soluzione: a) 1.4 cm; b) 500 Kcal; c) 154 cal/°K; d) 930 g
2B) Due moli di gas perfetto monoatomico alla pressione e volume iniziali p1 = 6 atm,
V1 = 15 litri, compiono un ciclo reversibile costituito da:
1-2: espansione adiabatica fino al volume V2 = 3V1;
2-3: compressione isoterma fino al volume V3 = V1;
3-1: compressione isocora fino allo stato iniziale.
Si chiede:
a) determinare le coordinate termodinamiche degli stati 1, 2, 3 e disegnare il ciclo;
b) determinare il lavoro complessivo compiuto dal gas durante il ciclo;
c) determinare il calore complessivo scambiato dal gas durante il ciclo;
d) determinare il rendimento del ciclo.
Soluzione: b) 2.3 KJ; c) 2.3 KJ; d) 33%
3B) Primo principio della Termodinamica: illustrare e fare qualche esempio
4B) Ciclo di Carnot
1C) Una persona con superficie corporea S=1.8 m2, indossa un abito spesso 1 cm di
conduttività termica K=10-5 Kcal/sec m °K. Se la temperatura cutanea e' 37°C e la
temperatura esterna e' 0°C:
a) calcolare il calore che si trasmette per conduzione attraverso gli abiti nell'unita' di
tempo;
b) valutare se la persona e' sufficientemente coperta, calcolando la perdita di calore
in 1 ora e confrontandola con il metabolismo basale di un soggetto in attività
moderata (produzione di ~100Kcal/h);
c) determinare la variazione di entropia dell'universo legata alla perdita di calore in 1
ora, calcolata al punto b).
T6
Se la quantità di calore di cui al punto b) potesse essere usata per far evaporare dell'acqua
bollente, calcolare:
d) la quantità di vapore prodotto.
Soluzione: a) 66.6 cal/s; b) ∆Q = 240 Kcal; c) 105 cal/°K; d) 444 g
2C) Due moli di gas perfetto monoatomico alla pressione e volume iniziali p1 = 6 atm,
V1 = 15 litri, compiono un ciclo reversibile costituito da:
1-2: espansione isoterma fino al volume V2 = 3V1;
2-3: contrazione isobara fino al volume V3;
3-1: compressione adiabatica fino allo stato iniziale.
Si chiede:
a) determinare le coordinate termodinamiche degli stati 1, 2, 3 e disegnare il ciclo;
b) determinare il lavoro complessivo compiuto dal gas durante il ciclo;
c) determinare il calore complessivo scambiato dal gas durante il ciclo;
d) determinare il rendimento del ciclo.
Soluzione: b) 1.9 KJ; c) 1.9 KJ; d) 19%
3C) Dilatazione termica: illustrare e fare qualche esempio
4C) Entropia del gas perfetto
1D) Una parete di superficie S = 3 m2 ha spessore 40 cm. La superficie esterna si trova a
Test = -20°C e quella interna a Tint = +20°C. Si osserva che la velocità di propagazione del
calore per conduzione attraverso la parete e' di 92 cal/sec. Determinare:
a) il coefficiente di conducibilità termica del materiale di cui e' fatta la parete;
b) la quantità di calore che attraversa la parete in 15 min;
c) la variazione di entropia dell'universo corrispondente a b).
Se la quantità di calore di cui al punto b) potesse essere ceduta a una miscela di acqua e
ghiaccio, calcolare:
d) la quantità di ghiaccio che si potrebbe fondere.
Soluzione: a) 0.31 cal/s•m•°K; b) 82.8 Kcal; c) 44.7 cal/°K; d) 1 Kg circa
2D) Due moli di gas perfetto monoatomico alla pressione e volume iniziali p1 = 6 atm,
V1 = 15 litri, compiono un ciclo reversibile costituito da:
1-2: espansione adiabatica fino al volume V2 = 3V1;
2-3: compressione isoterma fino lla pressione p3 = p1;
3-1: trasformazione isobara fino allo stato iniziale.
Si chiede:
a) determinare le coordinate termodinamiche degli stati 1, 2, 3 e disegnare il ciclo;
b) determinare il lavoro complessivo compiuto dal gas durante il ciclo;
c) determinare il calore complessivo scambiato dal gas durante il ciclo;
d) determinare il rendimento del ciclo.
Soluzione: b) 3.9 KJ; c) 3.9 KJ; d) 33%
T7
3D) Secondo principio della Termodinamica
4D) Potenziali termodinamici
Prova scritta del 18/2/1998
Una quantità di calore pari a 300 KJ viene fornita a 720 g di ghiaccio, che si trovano a
temperatura -10°C, utilizzando un termostato a t = 27°C. Calcolare:
a) la temperatura finale dell’acqua allo stato liquido;
b) la variazione di entropia del termostato;
c) la variazione di entropia dell’universo.
Soluzione: a) 288 °K; b) –103 J/°K; c) 96.5 J/°K
Prova scritta del 10/6/1998
Una mole di gas perfetto biatomico alla pressione pA = 2 atm e volume VA = 10 litri, esegue
un ciclo reversibile costituto da:
> un’espansione AB a pressione costante fino a VB = 3VA
> una compressione lungo una trasformazione lineare BC fino a pC= 1 atm e TC= TA
> una compressione isoterma fino a ritornare allo stato iniziale.
a) Disegnare il ciclo nel piano p,V
Calcolare:
b) il lavoro compiuto lungo ciascuna trasformazione;
c) il rendimento del ciclo.
Soluzione: b) 40 litri•atm, –15 litri•atm, -13.9 litri•atm; c) 8%
Prova scritta del 10/7/1998
Una quantità di ossigeno pari a m = 128 g (gas perfetto biatomico M=32), inizialmente alla
temperatura di 25°C, viene compresso reversibilmente e isotermicamente
da p1= 105 atm a p2= 6 p1. Calcolare:
a) i parametri dello stato iniziale e finale;
b) il calore scambiato (indicare se e’ calore assorbito o ceduto);
c) la variazione di entropia lungo la trasformazione.
Soluzione: b) –175 litri•atm; c) –0.6 litri•atm/ °K
Prova scritta parziale del 5/1/1999
1A) Una massa m1= 2 Kg di acqua alla temperatura t1= 80°C viene mescolata, in un
recipiente adiabatico, con una massa di ghiaccio m2= 1 Kg a t2= 0°C. Calcolare:
a) la temperatura finale del sistema;
b) la quantità di calore ceduta dall’acqua;
c) la variazione di entropia dell’Universo.
Soluzione: a) 27 °C; b) –106 Kcal; c) 62 cal/°K
T8
2A) Un cilindro munito di pistone contiene una quantità m = 60 g di aria. Le pareti del
cilindro, cosi’ come il pistone, sono impermeabili al calore. Inizialmente il pistone e’ bloccato
in una posizione tale che il volume iniziale dell’aria e’ Vi = 16.4 litri. Sul pistone agisce la
pressione atmosferica p0 = 1 atm. Ad un certo istante il pistone viene lasciato libero di
muoversi e si vede che l’aria si espande finche’ non raggiunge un volume
Vf = 39.8 litri. Considerando che si tratta di un processo adiabatico irreversibile, e trattando
l’aria come un gas perfetto biatomico di peso molecolare 30, si calcoli:
a) il lavoro compiuto dall’aria nell’espansione;
b) la variazione di energia interna del gas durante l’espansione;
c) temperatura e pressione iniziali dell’aria;
d) la variazione di entropia dell’aria;
e) la variazione di entalpia dell’aria.
Soluzione: a) 23.4 litri•atm; b) –23.4 litri•atm; c) 300 °K, 3 atm; d) 6.1 J/°K; e) –791 cal
1) Secondo principio della termodinamica
2) Equazioni di Poisson per trasformazioni adiabatiche reversibili di un gas perfetto
2B) Un cilindro munito di pistone contiene 2 moli di un gas perfetto biatomico. Le pareti del
cilindro, cosi’ come il pistone, sono impermeabili al calore. Inizialmente il pistone e’ bloccato
in una posizione tale che il gas si trova a una pressione pi = 3 atm e alla temperatura Ti = 300°K.
Sul pistone agisce la pressione atmosferica p0 = 1 atm. Ad un certo istante il pistone viene
lasciato libero di muoversi e si vede che il gas si espande finche’ non raggiunge una condizione
di equilibrio con la pressione esterna. In tale situazione si ha Tf = 243°K. Considerando che si
tratta di un processo adiabatico irreversibile, si calcoli:
a) la variazione di energia interna del gas durante l’espansione;
b) il lavoro compiuto dal gas nell’espansione;
c) il volume finale del gas;
d) la variazione di entropia del gas;
e) la variazione di entalpia del gas.
Soluzione: a) 23.4 litri•atm; b) ; c) 39.8 l; d) 0.06 litri•atm/ °K; e) ncp(Tf-Ti)
1) Gas perfetti e gas reali
2) Equazioni di Poisson per trasformazioni adiabatiche reversibili di un gas perfetto
Prova scritta del 19/2/1999
Una mole di gas perfetto monoatomico effettua un ciclo reversibile costituito da quattro
trasformazioni: compressione isocora (da A a B), espansione isobara (da B a C), espansione
adiabatica (da C a D) e compressione isoterma (da D a A). Assumendo TA = 313 °K, VA =
10 litri, TB = 533 °K, TC = 753 °K, calcolare:
a) i parametri termodinamici per ogni stato e disegnare il ciclo nel piano p-V;
b) il calore Q scambiato in ogni trasformazione;
c) il rendimento del ciclo;
d) il lavoro L compiuto dal gas in un ciclo.
Soluzione: b); c) 41%; d) 3 KJ
T9
A) Gas perfetti e gas reali
B) Dimostrare la relazione cp – cV = R valida per un gas perfetto
Prova scritta del 16/6/1999
In un recipiente a pareti adiabatiche e' contenuta una massa m = 0.5 Kg di paraffina alla
temperatura di 20°C. Nel recipiente viene versata una quantità M = 1 Kg di acqua alla
temperatura di 100°C. Calcolare:
a) la temperatura finale di equilibrio del sistema;
b) la variazione di entropia del sistema acqua+paraffina.
Per la paraffina si assumano i seguenti valori:
calori specifici:
solida cs = 0.42 cal/gr °C
liquida cl = 0.52 cal/gr °C
calore latente di fusione λ f = 35 cal/gr
temperatura di fusione t f = 55 °C
Soluzione: a) 71 °C; b) 8.6 cal/°K
Prova scritta del 12/7/1999
Un frigorifero e' dotato di un motore della potenza di 1.5 W e il suo coefficiente di prestazione e'
0.7 volte quello di un ciclo frigorifero di Carnot. Sapendo che il frigorifero lavora in una stanza
la cui temperatura e' t s = 25°C e che al suo interno la temperatura e'
ti = -5°C, calcolare:
a) il coefficiente di prestazione del frigorifero;
b) la quantità di calore che in un'ora viene sottratta dall'interno del frigorifero;
c) la quantità di calore che in un'ora viene ceduta alla stanza.
Soluzione: a) 6.25; b) 3.4•104 J; c) 3.9•104 J
Prova scritta del 20/9/1999
Una mole di gas perfetto monoatomico, inizialmente alla temperatura TA = 400°K, e volume VA =
20 litri, esegue un ciclo reversibile formato da una espansione isoterma fino ad un volume VB=
32.8 litri, una compressione isobara BC fino a tornare al volume iniziale e una trasformazione
isocora CA. Calcolare:
a) i parametri termodinamici di ogni stato e disegnare il ciclo nel piano p-V;
b) il calore scambiato in ogni trasformazione;
c) il rendimento del ciclo;
d) la variazione di entropia lungo la trasformazione isoterma.
Soluzione: b) 16.2 litri•atm, -32 litri•atm, 19.2 litri•atm; c) 9.6%; d) 0.04 litri•atm/ °K
T10