corso di laurea in matematica

CORSO DI LAUREA IN MATEMATICA
PRESENTAZIONE
La Matematica è disciplina di base e di supporto per tutta la ricerca
scientifica e tecnologica.
Anche se storicamente i suoi legami più profondi sono quelli con la
Fisica, nell’ultimo secolo la Matematica è diventata strumento essenziale
per l’informatica, la biologia, l’economia..., discipline dalle quali la
ricerca matematica trae stimoli e problemi, al punto che diventa sempre
meno definita la tradizionale distinzione tra Matematica Pura e
Matematica Applicata.
Ai filoni tradizionali dell’Algebra, Analisi, Fisica Matematica, Geometria,
Logica Matematica si è affiancato quello della Matematica
Computazionale e almeno le nozioni basilari di questi settori della
Matematica debbono ormai far parte della cultura scientifica di base non
solo di chi voglia dedicarsi alla ricerca, ma anche di coloro che sono
impegnati professionalmente nel campo delle applicazioni economiche,
tecnologiche e industriali.
La presente guida contiene le principali informazioni sull’organizzazione
dei seguenti corsi:
Corso di Laurea di primo livello in Matematica
Corso di Laurea Specialistica in Matematica
Corso di Laurea in Matematica (Vecchio Ordinamento,
quadriennale).
Nell’anno accademico 2003/2004 saranno attivati il primo, il secondo e il
terzo anno della Laurea di primo livello in Matematica , il primo anno
della Laurea Specialistica in Matematica, nonché il quarto anno della
Laurea in Matematica (Vecchio Ordinamento, quadriennale).
Gli studenti già iscritti alla Laurea o al Diploma in Matematica potranno,
a richiesta, optare per il passaggio alla Laurea di primo livello. Il
riconoscimento e la valutazione in crediti degli esami già sostenuti sarà
discusso caso per caso dal Consiglio di Area Didattica.
CORSO DI LAUREA DI PRIMO LIVELLO
IN MATEMATICA
(nuovo ordinamento)
ASPETTI GENERALI
La durata normale del Corso di Laurea di primo livello è di tre anni. Il
conseguimento della Laurea comporta l’acquisizione di 180 Crediti
Formativi Universitari distribuiti in media in numero pari a 60 per ogni
anno.
Il credito formativo universitario è l’unità di misura del lavoro di
apprendimento necessario allo studente per l’espletamento delle attività
formative prescritte per il conseguimento del titolo di studio. Ad un
credito corrispondono 25 ore di lavoro di apprendimento comprensivo di
ore di lezione, di esercitazione, di laboratorio, di seminario e di altre
attività formative, ivi comprese le ore di studio individuale.
OBIETTIVI FORMATIVI
È obiettivo specifico del Corso di Laurea di primo livello in Matematica
formare figure professionali che
-
posseggano adeguate conoscenze di base nell'area della matematica;
posseggano competenze computazionali ed informatiche;
abbiano acquisito le metodiche disciplinari e siano in grado di
comprendere e utilizzare descrizioni e modelli matematici di
situazioni concrete di interesse scientifico o economico;
siano in grado di utilizzare almeno una lingua dell'Unione Europea,
oltre l'italiano, nell'ambito specifico di competenza e per lo scambio
di informazioni generali;
posseggano adeguate competenze e strumenti per la comunicazione
e la gestione dell'informazione;
siano capaci di lavorare in gruppo, di operare con definiti gradi di
autonomia e di inserirsi prontamente negli ambienti di lavoro.
I laureati in matematica svolgeranno attività professionali nel campo della
diffusione della cultura scientifica, nonché del supporto modellistico-
matematico e computazionale ad attività dell'industria, della finanza, dei
servizi e della pubblica amministrazione.
Ai fini indicati, i curricula del corso di laurea in Matematica
1
Comprendono in ogni caso attività finalizzate a
far acquisire:
le conoscenze fondamentali nei vari campi della
matematica, nonché di metodi propri della
matematica nel suo complesso,
la modellizzazione di fenomeni naturali, sociali ed economici e di
problemi tecnologici,
le tecniche di calcolo numerico e simbolico e gli
aspetti computazionali della matematica e della
statistica .
2 Prevedono una quota significativa di attività formative caratterizzate
da un particolare rigore logico e da un elevato livello di astrazione;
3 Prevedono, in relazione ad obiettivi specifici, l'obbligo di attività
esterne, come tirocini formativi presso aziende, strutture della
pubblica amministrazione e laboratori, oltre a soggiorni di studio
presso altre università italiane o estere, anche nel quadro di accordi
internazionali.
REQUISITI PER L’ACCESSO
Per accedere al Corso di Laurea di primo livello in Matematica è
necessario essere in possesso di un diploma di scuola secondaria superiore
di durata quinquennale o di altro titolo di studio conseguito all’estero,
riconosciuto idoneo sulla base della normativa vigente.
Sono richieste preparazione culturale e adeguata conoscenza degli
elementi di base della matematica normalmente fornite dalla scuola media
superiore.
Il Consiglio di Corso di Laurea in Matematica potrà proporre al Consiglio
di Facoltà l'attivazione di opportune prove di verifica, che saranno di
norma organizzate entro il mese di settembre, prima dell'inizio delle
ordinarie attività didattiche.
In relazione alle esigenze, saranno previste attività formative di tipo
propedeutico per l'ammissione al primo anno e corsi di integrazione delle
conoscenze generali richieste dalla didattica universitaria.
Potranno essere realizzati e diffusi nelle scuole secondarie, anche per via
telematica, test di autovalutazione che consentano agli studenti di
verificare il loro effettivo grado di preparazione e di ricevere indicazioni
circa gli strumenti con cui ovviare alle eventuali lacune riscontrate.
PIANO DIDATTICO
Le attività didattiche del Corso di Laurea di primo livello in Matematica
saranno di norma organizzate in semestri, con inizio il 1 Ottobre, con
interruzione nel mese di febbraio e con temine nel mese di giugno. Agli
studenti iscritti è richiesta di norma la frequenza continuativa agli
insegnamenti previsti nei rispettivi curricula di laurea.
Saranno previste di norma tre sessioni d'esami, nei mesi di febbraio,
giugno-luglio e settembre. Nella sessione di febbraio saranno previsti due
appelli per gli insegnamenti del primo semestre, nella sessione di giugnoluglio saranno previsti due appelli per gli insegnamenti del secondo
semestre. Durante il periodo di svolgimento degli esami le lezioni saranno
sospese. L'acquisizione dei crediti avverrà al momento dell'esame, che
darà luogo anche a valutazione in trentesimi.
Acquisiti i necessari 177 crediti formativi, lo studente è ammesso a
sostenere la prova finale per il conseguimento del titolo. La prova finale,
che consente di acquisire i restanti 3 crediti, consiste di norma nella
discussione di un elaborato scritto preparato dallo studente, e dà luogo al
voto finale di laurea, espresso in centodecimi.
Il calendario preciso delle attività didattiche e formative, degli esami
nonché la struttura e l'articolazione precisa di ogni insegnamento, con
l'indicazione di ogni elemento utile per la relativa fruizione da parte degli
studenti iscritti, sono specificati annualmente nel manifesto degli studi e
nella guida ai corsi di studio predisposta dalla facoltà.
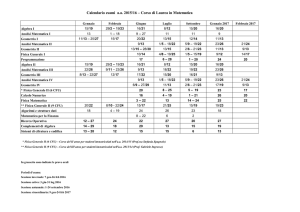
Per l’anno accademico 2003/2004 è previsto il
seguente calendario:
Lezioni
Semestre
Primo
Secondo
Data di inizio
1 ottobre 2003 (primo anno)
6 ottobre 2003 (anni successivi)
8 marzo 2004
Data di fine
23 gennaio 2004
31 maggio 2004
Esami
Sessione
Prima
Seconda
Terza
Data di inizio
2 febbraio 2004
9 giugno 2004
1 settembre 2004
Data di fine
5 marzo 2004
31 luglio 2004
30 settembre 2004
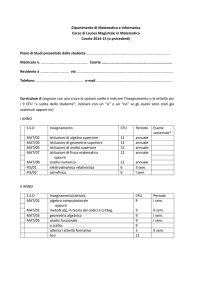
ELENCO DEGLI INSEGNAMENTI E DELLE ALTRE ATTIVITÀ
FORMATIVE
Il Corso di laurea di primo livello in Matematica si articola in quattro
curricula:
Matematica ad indirizzo generale,
Matematica per il trattamento dell'informazione,
Matematica per la didattica, la formazione e la divulgazione
scientifica,
Matematica per le applicazioni all'industria e alla tecnologia.
Sono insegnamenti comuni a tutti i curricula:
Anno di
corso/sem
e
stre
1/1
1/1
1/1
1/1
1/2
1/2
1/2
1/2
1/2
2/1
2/1
2/1
Denominazione
Settore
Crediti
Matematica di Base
MAT/01,02,0
3,04,05, 07,
08
MAT/05
MAT/03
INF/01
6
8
8
6
MAT/02
MAT/05
MAT/03
MAT/08
7
7
7
8
MAT/02
MAT/05
MAT/03
3
6
6
6
Analisi Matematica I
Geometria I
Fondamenti di Informatica e
Laboratorio
Algebra I
Analisi Matematica II
Geometria II
Laboratorio di Programmazione
e Calcolo
Lingua Straniera
Algebra II
Analisi Matematica III
Geometria III
2/1
2/1
2/1
2/2
2/2
2/2
3/1
3/1
Fisica Generale I
Laboratorio Fisica Generale I
Lingua Straniera
Fisica Matematica
Teoria dell’Informazione
Calcolo Numerico
Fisica Generale II
Analisi Matematica IV
Scelta autonoma
Altre attività
Prova finale
FIS/01
FIS/01
MAT/07
INF/01
MAT/08
FIS/01
MAT/05
6
3
3
6
6
6
6
6
9
9
3
I rimanenti insegnamenti, per un totale di 39 crediti, dipendono dal
curriculum scelto (si veda il successivo punto 6).
Totale CFU 180
CURRICULA OFFERTI AGLI STUDENTI
I curricula previsti dalla laurea di primo livello in Matematica sono i
seguenti: “Matematica ad indirizzo generale”, “Matematica per il
trattamento dell’informazione”, “Matematica per la didattica, la
formazione e la divulgazione scientifica”, “Matematica per le
applicazioni all’industria e alla tecnologia”.
Curriculum Matematica ad indirizzo generale
Il curriculum “Matematica ad indirizzo generale” si prefigge di fornire
approfondite conoscenze di base nell’area della matematica ed un elevato
livello di astrazione e di autonomia nella risoluzione dei problemi.
I crediti acquisiti nel percorso comune dovranno essere completati nel
modo seguente:
Anno di
corso/seme
stre
2/2
3/1
3/
3/
3/
Denominazione
Settore
Crediti
Logica Matematica I
Laboratorio di Fisica II
Un insegnamento del gruppo A
Un insegnamento del gruppo A
Un insegnamento del gruppo A
MAT/01
FIS/01
MAT
MAT
MAT
6
3
6
6
6
3/
3/
Un insegnamento del gruppo A
Un insegnamento del gruppo A
MAT
MAT
6
6
Gruppo A
Anno di
corso/seme
stre
3/
3/
3/
3/
3/
3/
3/
3/
3/
Denominazione
Settore
Crediti
Algebra III
Algebra IV
Analisi Matematica V
Analisi Matematica VI
Geometria IV
Geometria V
Geometria VI
Fisica Matematica II
Equazioni Differenziali
MAT/02
MAT/02
MAT/05
MAT/05
MAT/03
MAT/03
MAT/03
MAT/07
MAT/05
6
6
6
6
6
6
6
6
6
Curriculum Matematica per il trattamento dell’informazione
Il curriculum “Matematica per il trattamento dell’informazione” si
prefigge di fornire un’elevata conoscenza pratica e teorica degli strumenti
matematici fondamentali per l’informatica con particolare riferimento al
trattamento dell’informazione di natura numerica e simbolica.
I crediti acquisiti nel percorso comune dovranno essere completati nel
modo seguente:
Anno di
corso/sem
e
stre
2/2
2/2
3/
3/
3/
Denominazione
Settore
Crediti
Teoria della Computabilità I
Linguaggi di Programmazione
Teoria della Computabilità II
Un insegnamento del gruppo B o
due moduli
Un insegnamento del gruppo C o
due moduli
MAT/01
INF/01
MAT/01
6
3
6
6
6
3/
3/
Un insegnamento del gruppo C o
due moduli
Un insegnamento caratterizzante
6
6
Gruppo B
Anno di
corso/sem
e
stre
3/
3/
3/
3/
3/
Denominazione
Settore
Logica Matematica II
MAT/01
Teoria dei grafi
MAT/03
Semigruppi liberi e teoria di codici MAT/02
Fisica dell’Informazione
FIS/02
Calcolo delle Probabilità e Statistica MAT/06
Crediti
6
3
3
3
3
Gruppo C
Anno di
corso/sem
e
stre
3/
3/
3/
3/
3/
3/
3/
Denominazione
Settore
Crediti
Teoria delle Funzioni
Clacolo Numerico II
Intelligenza Artificiale
Teoria dei Giochi
Metodi per il Trattamento
dell’Informazione
Data-Base
Geometria Combinatoria
MAT/05
MAT/08
INF/01
MAT/05
INF/01
6
6
3
3
6
INF/01
MAT/03
3
3
MAT/02
MAT/02
MAT/05
MAT/05
MAT/05
MAT/05
6
6
6
6
6
3
Insegnamenti caratterizzanti attivati
3/
3/
3/
3/
3/
3/
Algebra III
Algebra IV
Analisi Matematica V
Analisi Matematica VI
Analisi Funzionale I
Analisi Funzionale II
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
Analisi Numerica
Calcolo delle Probabilità e
Statistica
Clacolo Numerico II
Equazioni Differenziali
Fisica Matematica II
Fondamenti di Geometria
Geometria IV
Geometria V
Geometria VI
Logica Matematica II
Matematiche complementari II
Matematiche elementari da un
punto di vista superiore
Ricerca Operativa
Semigruppi liberi e teoria di
codici
Storia delle Matematiche
Teoria dei grafi
Teoria dei Numeri
Teoria della Computabilità II
Teoria delle Funzioni
MAT/08
MAT/06
6
3
MAT/08
MAT/05
MAT/07
MAT/03
MAT/03
MAT/03
MAT/03
MAT/01
MAT/04
MAT/04
6
6
6
3
6
6
6
6
6
6
MAT/09
MAT/02
6
3
MAT/04
MAT/03
MAT/02
MAT/01
MAT/05
6
3
3
6
6
Curriculum Matematica per la didattica, la formazione e la
divulgazione scientifica
Il curriculum “Matematica per la didattica, la formazione e la
divulgazione scientifica” si prefigge di fornire competenze relative alla
storia ed alla epistemologia della matematica, nonché competenze della
metodologia di trasmissione della conoscenza scientifica.
I crediti acquisiti nel percorso comune dovranno essere completati nel
modo seguente:
Anno di
corso/sem
e
stre
2/2
2/2
Denominazione
Settore
Crediti
Matematiche Complementari I
Laboratorio di Matematica
Computazionale
MAT/04
INF/01
6
3
3/
3/
3/
3/
3/
3/
Laboratorio di Fisica II
Chimica
Un insegnamento del gruppo D
Un insegnamento del gruppo D
(o due moduli)
Un insegnamento caratterizzante
a scelta
Un insegnamento caratterizzante
a scelta
FIS/01
CHIM/03,06
MAT/
MAT/
3
6
6
6
MAT/
6
MAT/
3
Denominazione
Settore
Crediti
Matematiche complementari II
Matematiche elementari da un
punto di vista superiore
Storia delle Matematiche
Fondamenti di Geometria
Teoria dei Numeri
Analisi Funzionale I
MAT/04
MAT/04
6
6
MAT/04
MAT/03
MAT/02
MAT/05
6
3
3
6
MAT/02
MAT/02
MAT/05
MAT/05
MAT/05
MAT/05
MAT/08
MAT/06
6
6
6
6
6
3
6
3
MAT/08
MAT/05
MAT/07
MAT/03
6
6
6
3
Gruppo D
Anno di
corso/sem
e
stre
3/
3/
3/
3/
3/
3/
Insegnamenti caratterizzanti attivati
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
Algebra III
Algebra IV
Analisi Matematica V
Analisi Matematica VI
Analisi Funzionale I
Analisi Funzionale II
Analisi Numerica
Calcolo delle Probabilità e
Statistica
Clacolo Numerico II
Equazioni Differenziali
Fisica Matematica II
Fondamenti di Geometria
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
Geometria IV
Geometria V
Geometria VI
Logica Matematica II
Matematiche complementari II
Matematiche elementari da un
punto di vista superiore
Ricerca Operativa
Semigruppi liberi e teoria di
codici
Storia delle Matematiche
Teoria dei grafi
Teoria dei Numeri
Teoria della Computabilita’ II
Teoria delle Funzioni
MAT/03
MAT/03
MAT/03
MAT/01
MAT/04
MAT/04
6
6
6
6
6
6
MAT/09
MAT/02
6
3
MAT/04
MAT/03
MAT/02
MAT/01
MAT/05
6
3
3
6
6
Curriculum Matematica per le applicazioni all'industria e alla
tecnologia
Il curriculum “Matematica per le applicazioni all'industria e alla
tecnologia” si prefigge di fornire un’elevata capacità di trattamento di
informazioni di carattere non solo numerico, nonché un’alta competenza
teorica e pratica delle strutture di calcolo.
I crediti acquisiti nel percorso comune dovranno essere completati nel
seguente modo:
Anno di
corso/sem
e
stre
2/2
3/
3/
3/
3/
3/
3/
Denominazione
Settore
Crediti
Logica Matematica I
Un insegnamento del gruppo E
Un insegnamento del gruppo E
Un insegnamento del gruppo E
Un insegnamento affine
Un insegnamento caratterizzante
a scelta
Un insegnamento caratterizzante
a scelta
MAT/01
MAT/
6
6
6
6
6
6
MAT/
3
Gruppo E
Anno di
corso/sem
e
stre
3/
3/
3/
3/
Denominazione
Settore
Crediti
Analisi Numerica
Fisica Matematica II
Ricerca Operativa
Teoria dell’Informazione II
MAT/08
MAT/07
MAT/09
INF/01
6
6
6
6
MAT/02
MAT/02
MAT/05
MAT/05
MAT/05
MAT/05
MAT/08
MAT/06
6
6
6
6
6
3
6
3
MAT/08
MAT/05
MAT/07
MAT/03
MAT/03
MAT/03
MAT/03
MAT/01
MAT/04
MAT/04
6
6
6
3
6
6
6
6
6
6
MAT/09
MAT/02
6
3
MAT/04
MAT/03
6
3
Insegnamenti caratterizzanti attivati
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
3/
Algebra III
Algebra IV
Analisi Matematica V
Analisi Matematica VI
Analisi Funzionale I
Analisi Funzionale II
Analisi Numerica
Calcolo delle Probabilità e
Statistica
Clacolo Numerico II
Equazioni Differenziali
Fisica Matematica II
Fondamenti di Geometria
Geometria IV
Geometria V
Geometria VI
Logica Matematica II
Matematiche complementari II
Matematiche elementari da un
punto di vista superiore
Ricerca Operativa
Semigruppi liberi e teoria di
codici
Storia delle Matematiche
Teoria dei grafi
3/
3/
3/
Teoria dei Numeri
Teoria della Computabilita’ II
Teoria delle Funzioni
MAT/02
MAT/01
MAT/05
3
6
6
L’insegnamento affine potrà essere scelto tra tutti
gli insegnamenti attivati nei corsi di laurea della
Facolta’.
INSEGNAMENTI ATTIVATI PER L’ANNO
ACCADEMICO 2003/2004
I ANNO
I SEMESTRE
Matematica di base (6 CFU)
Analisi Matematica I (8 CFU)
Geometria I (8 CFU)
Fondamenti di Informatica e
Laboratorio (6 CFU)
Analisi Matematica II
(7 CFU)
Geometria II (7 CFU)
II SEMESTRE Algebra I (7 CFU)
Laboratorio di Programmazione e Calcolo (8 CFU)
I ANNO
Docente: M. Maj
Docente: M. Transirico
Docente: G. Sparano
Docente: D. Parente
Docente:M. Transirico
Docente: G. Sparano
Docente: M. Maj
Docente: G. Capobianco
Analisi Matematica III
(6 CFU)
Geometria III (6 CFU)
Algebra II (6 CFU)
Teoria dell’Informazione
(6 CFU)
Docente: L. Sgambati
II ANNO
II SEMESTRE
Curriculum
Matematica ad
Indirizzo
Generale
Fisica Matematica (6 CFU)
Fisica Generale I (6 CFU)+
Laboratorio di Fisica
Generale I (3 CFU)
Calcolo Numerico (6 CFU)
Logica Matematica I (6 CFU)
Docente: E. Laserra
Docenti: M. FuscoGirard, A. Cucolo
II ANNO
II SEMESTRE
Curriculum
Matematica per
la Didattica la
Formazione e
la Divulgazione
Fisica Matematica (6 CFU)
Fisica Generale I (6 CFU)+
Laboratorio di Fisica
Generale I (3 CFU)
Calcolo Numerico (6 CFU)
Matematiche Complementari
I (6 CFU)
Docente: E. Laserra
Docenti: M. FuscoGirard, A. Cucolo
II ANNO
I SEMESTRE
Docente: A. Di Concilio
Docente:P. Longobardi
Docente: V. Giorno
Docente: M.R. Crisci
Docente: A. Di Nola
Docente: M.R. Crisci
Docente: F. Palladino
Scientifica
Laboratorio di Matematica
Computazionale (3 CFU)
Docente: G. Capobianco
II ANNO
II SEMESTRE
CURRICULUM
Matematica per
le Applicazioni
all’Industria e
alla Tecnologia
Fisica Matematica (6 CFU)
Fisica Generale I (6 CFU)+
Laboratorio di Fisica
Generale I (3 CFU)
Calcolo Numerico (6 CFU)
Logica Matematica I (6 CFU)
Docente: E. Laserra
Docenti: M. Fusco-Gi
rard, A. Cucolo
II
ANNO-II
SEMESTRE
CURRICULUM
Matematica per
il Trattamento
dell’Informazione
Fisica Matematica (6 CFU)
Docente: E. Laserra
Fisica Generale I (6 CFU)+
Docenti: M. FuscoLaboratorio di Fisica
Girard, A. Cucolo
Generale I (3 CFU)
Calcolo Numerico (6 CFU)
Docente: M.R. Crisci
Teoria della Computabilità I Docente: G. Gerla
(6 CFU)
Linguaggi di ProgrammaDocente: M. Napoli
zione (3 CFU)
Docente: M.R. Crisci
Docente: A. Di Nola
Inoltre gli studenti del primo e del secondo anno dovranno acquisire 6
crediti di Lingua Straniera
III ANNO
I SEMESTRE
Analisi Matematica IV (6
CFU)
Fisica Generale II (6 CFU)
Docente: L. Sgambati
Docenti:
Girard
M.
Fusco-
Sono inoltre attivati i seguenti insegnamenti caratterizzanti
Analisi Matematica V (6
CFU)
Calcolo delle Probabilità (3
I SEMESTRE CFU)
Fisica Matematica II (6 CFU)
Geometria IV (6 CFU)
Laboratorio di Fisica
Generale II (3 CFU)
Matematiche Complementari
II (6 CFU)
III ANNO
Docente: A. Vitolo
Docente:
A.
De
Crescenzo
Docente: E. Laserra
Docente: A. Vinogradov
Docente:
Alfonso
Romano
Docente: G. Gerla
III ANNO
III
SEMESTRE
Storia delle Matematiche (6
CFU)
Teoria delle Funzioni (6 CFU)
Equazioni Differenziali (6
CFU)
Analisi Funzionale I (6 CFU)
Algebra IV (6 CFU)
Docente: F. Palladino
Algebra III (6 CFU)
Analisi Matematica VI (6
CFU)
Analisi Numerica (6 CFU)
Calcolo Numerico II (6 CFU)
Geometria V (6 CFU)
Geometria VI (6 CFU)
Matematiche Elementari da
un punto di vista superiore (6
CFU)
Metodi per il trattamento
dell’Informazione II (6 CFU)
Ricerca Operativa (6 CFU)
Docente: M. Maj
Docente: A. Vitolo
Logica Matematica II (6
CFU)
Semigruppi liberi e Teoria dei
Codici (3 CFU)
Teoria dei Numeri (3 CFU)
Teoria della Computabilità II
(6 CFU)
Teoria dei Grafi (3 CFU)
Fondamenti di Geometria (3
CFU)
Teoria dell’Informazione II
(6 CFU)
Analisi Funzionale II (3
CFU)
Docente: V. Cafagna
Docente: M. Transirico
Docente: L. Sgambati
Docente: G. Vincenzi
Docente: E. Russo
Docente: E. Russo
Docente: A. Vinogradov
Docente: A. Di Concilio
Docente: F. Palladino
Docente: V. Giorno
Mutuato con omonimo
insegnamento del corso
di laurea in Informatica
Docente: A. Di Nola
Docente: P. Longobardi
Docente: P. Longobardi
Docente: G. Gerla
Docente: da definire
Docente: da definire
Mutuato con Metodi per
il
trattamento
dell’Informazione
Docente: L. Sgambati
CORSO DI LAUREA SPECIALISTICA
IN MATEMATICA
( nuovo ordinamento)
ASPETTI GENERALI
Il conseguimento della Laurea Specialistica in Matematica comporta
l’acquisizione di 300 Crediti Formativi Universitari (CFU) (di cui 180
già conseguiti nella laurea di primo livello).
OBIETTIVI FORMATIVI
I laureati nel Corso di Laurea Specialistica in Matematica devono:
- avere una solida preparazione culturale nell’area della matematica e
dei metodi propri della disciplina;
- conoscere approfonditamente il metodo scientifico;
- possedere avanzate competenze computazionali ed informatiche;
- avere conoscenze matematiche specialistiche, anche contestualizzate
ad altre scienze, all’ingegneria e ad altri campi applicativi;
- essere in grado di analizzare e risolvere problemi complessi, anche in
contesti applicativi;
- essere in grado di riconoscere e di costruire i diversi modelli
matematici nelle applicazioni scientifiche, industriali ed economiche;
- aver acquisito specifiche capacità per la comunicazione dei problemi e
dei metodi della matematica;
- essere in grado di utilizzare fluentemente, in forma scritta e orale,
almeno una lingua dell'Unione Europea oltre l'italiano con riferimento
anche ai lessici disciplinari ;
- avere capacità relazionali e decisionali, ed essere capaci di lavorare
con ampia autonomia, anche assumendo responsabilità scientifiche ed
organizzative.
I laureati nei corsi di laurea specialistica della classe potranno
esercitare funzioni di elevata responsabilità nella costruzione e nello
sviluppo computazionale di modelli matematici di varia natura, in diversi
ambiti applicativi scientifici, ambientali, sanitari, industriali, finanziari,
nei servizi e nella pubblica amministrazione; nei settori della
comunicazione della matematica e della scienza.
Ai fini indicati, i curricula dei corsi di laurea della classe
comprendono:
- attività formative che si caratterizzano per un particolare rigore
logico e per un livello elevato di astrazione;
- attività di laboratorio computazionale e informatico, in particolare
dedicate alla conoscenza di applicazioni informatiche, ai linguaggi
di programmazione e al calcolo;
- attività esterne, in relazione a obiettivi specifici, come tirocini
formativi presso aziende e laboratori e soggiorni di studio presso
altre università italiane ed europee, anche nel quadro di accordi
internazionali.
PIANO DIDATTICO
Le attività didattiche del Corso di Laurea Specialistica in Matematica
saranno di norma organizzate in semestri, con inizio il 1 Ottobre, con
interruzione nel mese di febbraio e con temine nel mese di giugno. Agli
studenti iscritti è richiesta di norma la frequenza continuativa agli
insegnamenti previsti nei rispettivi curricula di laurea.
Saranno previste di norma tre sessioni d'esami, nei mesi di febbraio,
giugno-luglio e settembre. Nella sessione di febbraio saranno previsti due
appelli per gli insegnamenti del primo semestre, nella sessione di giugnoluglio saranno previsti due appelli per gli insegnamenti del secondo
semestre. Durante il periodo di svolgimento degli esami le lezioni saranno
sospese. L'acquisizione dei crediti avverrà al momento dell'esame, che
darà luogo anche a valutazione in trentesimi.
Nell ’anno accademico 2003/2004
seguente calendario:
Lezioni
Semestre
Primo
Secondo
Data di inizio
6 ottobre 2003
8 marzo 2004
è previsto il
Data di fine
23 gennaio 2004
31 maggio 2004
Esami
Sessione
Prima
Seconda
Terza
Data di inizio
2 febbraio 2004
9 giugno 2004
1 settembre 2004
Data di fine
5 marzo 2004
31 luglio 2004
30 settembre 2004
ELENCO DEGLI INSEGNAMENTI E DELLE ALTRE ATTIVITÀ
FORMATIVE
Nell’anno accademico 2003/2004 sono attivati i seguenti insegnamenti:
Algebra III
Algebra IV
Analisi Funzionale I
Analisi Funzionale II
Analisi Matematica V
Analisi Matematica VI
Calcolo Numerico II
Equazioni
Differenziali
Geometria V
Geometria IV
Geometria VI
Istituzioni di Fisica
Mat
Logica Matematica II
Storia delle
Matematiche
Teoria dei grafi
Teoria
dell’Informazione II
MAT/02
MAT/02
MAT/05
MAT/05
MAT/05
MAT/05
MAT/08
MAT/05
6 CFU
6 CFU
6 CFU
3 CFU
6 CFU
6 CFU
6 CFU
6 CFU
Docente M. Maj
Docente : G. Vincenzi
Docente : L. Sgambati
Docente : L. Sgambati
Docente : A. Vitolo
Docente: A. Vitolo
Docente : E. Russo
Docente: M. Transirico
MAT/03
MAT/03
MAT/03
MAT/07
6 CFU
6 CFU
6 CFU
6 CFU
Docente: A. Vinogradov
Docente: A. Vinogradov
Docente: A. Di Concilio
Docente : E. Laserra
MAT/01
MAT/04
6 CFU
6 CFU
Docente: A. Di Nola
Docente: F. Palladino
MAT/03
INF/01
3 CFU
6 CFU
Docente: V. Giorno
Lo studente potrà inoltre scegliere tra tutti gli insegnamenti caratterizzanti
attivati per la laurea triennale in matematica.
CORSO DI LAUREA IN MATEMATICA
(quadriennale – vecchio ordinamento)
La durata del Corso di Laurea in Matematica è di quattro anni. Il corso di
studi prevede quindici annualità di insegnamento, anche divisi in moduli
semestrali. L’articolazione del Corso di Laurea, i piani di studio con i
relativi insegnamenti fondamentali obbligatori, i moduli didattici, le
forme di tutorato, le prove di valutazione della preparazione degli
studenti, la propedeuticità degli insegnamenti, il riconoscimento degli
insegnamenti seguiti presso altri Corsi di Laurea e di Diploma, sono
determinati dal Consiglio di Corso di Laurea o di Area didattica, se
costituito, in armonia con le norme del regolamento di Facoltà e del
regolamento di Ateneo.
Il corso di studi del Corso di Laurea in Matematica è costituito da un
biennio propedeutico, a carattere formativo di base, e da un successivo
biennio (di indirizzo), articolato in tre indirizzi: generale, didattico,
applicativo.
Nell’anno accademico 2003/2004 verrà attivato il
4° anno del corso di laurea in Matematica (Vecchio
Ordinamento).
Gli insegnamenti del biennio propedeutico sono gli stessi per tutti gli
studenti, mentre quelli del secondo biennio sono in parte comuni ed in
parte dipendenti dal particolare indirizzo scelto.
L’iscrizione ai corsi per la Laurea in Matematica di studenti provenienti
da altri corsi di laurea o di diploma e la convalida degli esami superati
saranno stabiliti dal Consiglio di Corso di Laurea e dal Consiglio di
Facoltà.
Coloro che sono in possesso di altra laurea e che aspirano a conseguire la
laurea in Matematica, tenuto conto degli studi compiuti e degli esami
superati, possono ottenere una abbreviazione di corso, che viene stabilita
con decreto rettorale, udito, caso per caso, il Consiglio di Corso di Laurea
ed il Consiglio di Facoltà.
PIANI DI STUDIO
Ogni anno lo studente può proporre un piano
individuale in sostituzione di quello ufficiale o di
un precedente diverso piano individuale. La
proposta deve riguardare l’intero corso di studi e
deve prevedere lo stesso numero di insegnamenti
del piano di studi ufficiale. Il Consiglio di Corso di
Laurea, dopo aver analizzato e discusso il piano
individuale, accetta, accetta con modifiche o
respinge la proposta dello studente. Non si
indicano norme assolute per l’accettabilità dei
piani di studio. In linea di massima si ritiene che
gli insegnamenti del primo biennio così come gli
insegnamenti obbligatori del secondo biennio siano
insostituibili. Nei casi dubbi si consiglia
di
discutere la proposta con i responsabili dei tre
indirizzi.
Biennio di base
Sono obbligatori i seguenti insegnamenti comuni a tutti gli indirizzi
I ANNO
Algebra
Analisi Matematica I
Geometria
II ANNO
Fisica Generale I
Analisi Matematica II
Fisica Generale II
Geometria II
Meccanica Razionale
Gli insegnamenti sopra elencati sono accompagnati da un corso di
esercitazioni che ne è parte integrante.
Potranno essere iscritti al secondo anno gli studenti che abbiano superato
almeno due degli esami del primo anno.
Biennio di indirizzo
Potranno essere iscritti al terzo anno gli studenti che abbiano superato
almeno quattro degli esami del primo biennio.
All'atto dell'iscrizione al terzo anno ogni studente deve presentare un
piano di studi con l'indicazione dell'indirizzo e degli insegnamenti
opzionali prescelti.
Potranno essere iscritti al quarto anno gli studenti che abbiano dimostrato
la conoscenza della lingua inglese attraverso un colloquio, regolarmente
verbalizzato da una commissione nominata dal Consiglio di Facoltà.
Indirizzo generale
Sono obbligatori gli insegnamenti
annuali o entrambi i moduli di
un modulo di
un modulo a scelta tra
tre moduli a scelta tra
due moduli o una annualità
a scelta tra
Istituzioni di Analisi Superiore
Istituzioni di Geometria Superiore
Istituzioni di Algebra Superiore
Istituzioni di Fisica Matematica
Analisi Funzionale
Analisi Superiore
Equazioni Differenziali
Teoria delle Funzioni
Calcolo Numerico e Programmazione I
(primo modulo, secondo modulo)
Istituzioni di Algebra Superiore
(secondo modulo)
Istituzioni di Fisica Matematica
(secondo modulo)
Algebra Superiore
Analisi Funzionale
Geometria Superiore
Logica Matematica
Teoria delle Funzioni
Teoria dell’Informazione
Topologia
Lo studente dovrà infine scegliere due moduli o una annualità nel gruppo
degli insegnamenti opzionali attivati.
Indirizzo didattico
Sono obbligatori gli insegnamenti
annuali o entrambi i moduli di
Istituzioni di Analisi Superiore
Matematiche
un modulo di
due moduli o una annualità
a scelta tra
due moduli o una annualità
a scelta tra
Complementr
i
Istituzioni di Algebra Superiore
Istituzioni di Fisica Matematica
Istituzioni di Geometria Superiore
Logica Matematica
Storia delle Matematiche
Calcolo
Numerico
e
Programmazione I (primo modulo,
secondo modulo)
Teoria dell’Informazione
Lo studente dovrà infine scegliere tre moduli nel gruppo degli
insegnamenti opzionali attivati.
Indirizzo applicativo (orientamento numerico)
Sono obbligatori gli insegnamenti
annuali
o
entramb
i
i
moduli
di
un modulo di
due moduli o una annualità
a scelta tra
Istituzioni di Analisi Superiore
Calcolo
Numerico
Programmazione I
Teoria dell’Informazione
e
Istituzioni di Algebra Superiore
Istituzioni di Fisica Matematica
Istituzioni di Geometria Superiore
Analisi Funzionale
Analisi Superiore
Calcolo Numerico e
Programmazione II
Teoria delle Funzioni
Lo studente dovrà infine scegliere tre moduli nel gruppo degli
insegnamenti opzionali attivati.
Indirizzo applicativo (orientamento logico-informatico)
Sono obbligatori gli insegnamenti
annuali o entrambi i moduli Istituzioni di Analisi Superiore
Calcolo
Numerico
e
di
Programmazione I
Logica Matematica
Teoria dell’Informazione
un modulo di
Istituzioni di Algebra Superiore
Istituzioni di Fisica Matematica
Istituzioni di Geometria Superiore
due moduli o una annualità
Calcolo
Numerico
e
a scelta tra
Programmazione II
Matematiche Complementari (primo
modulo)
Lo studente dovrà infine scegliere un modulo nel gruppo degli
insegnamenti opzionali attivati.
Le strutture didattiche provvederanno a che almeno sei moduli semestrali
siano comuni per gli studenti del Corso di Laurea e del Corso di Diploma.
Per gli studenti in possesso del Diploma Universitario in Matematica le
strutture didattiche predisporranno, sentito lo studente, un piano di studi
individuale, anche in deroga alle precedenti disposizioni, che completi la
sua preparazione in relazione all'indirizzo prescelto.
Per conseguire la Laurea in Matematica il piano di
studio dovrà contenere in ogni caso l'equivalente di
almeno undici annualità scelte nelle aree
disciplinari della logica matematica, dell'algebra,
della geometria, delle matematiche complementari,
dell'analisi matematica, della probabilità e
statistica matematica, della fisica matematica,
dell'analisi numerica, della ricerca operativa.
In applicazione dell'art. 2 della legge 11 dicembre 1969 e dell'art. 4 della
legge 20 novembre 1970, n. 924, il Consiglio di Corso di Laurea potrà
approvare piani di studio individuali in deroga a quanto su previsto.
INSEGNAMENTI ATTIVATI PER L'A.A. 2003/4
CORSO DI LAUREA IN MATEMATICA
(quadriennale - vecchio ordinamento)
IV ANNO- I
Istituzioni di Geometria Superiore
(I modulo)
Istituzioni di Fisica Matematica (I
modulo)
Istituzioni di Algebra Superiore (I
modulo)
Matematiche Complementari (I
modulo)
Logica Matematica (I modulo)
Storia delle Matematiche (I
modulo)
Analisi Funzionale (I modulo)
Teoria dell’Informamazione (I
modulo)
Teoria delle Funzioni (I modulo)
Calcolo Numerico e
Programmazione I (I modulo)
Algebra Superiore (I modulo)
Equazioni Differenziali (I modulo)
SEMESTRE
Mutuato con Geometria IV, nuovo
ordinamento
Mutuato con Fisica Matematica,
nuovo ordinamento
Mutuato con Algebra II, nuovo
ordinamento
Mutuato con Matematiche
Complementari II, nuovo
ordinamento
Mutuato con Logica Matematica II,
nuovo ordinamento
Mutuato con Storia delle
Matematiche, nuovo ordinamento
Mutuato con Analisi Funzionale I,
nuovo ordinamento
Mutuato con Teoria
dell’Informazione, nuovo
ordinamento
Mutuato con Teoria delle Funzioni,
nuovo ordinamento
Docente: M..R. Crisci
Docente: G. Vincenzi
Mutuato con Equazioni
Differenziali, nuovo ordinamento
Ricerca operativa (I modulo)
Mutuato con l’analogo corso del
C.L. in Informatica
IV ANNO – SECONDO SEMESTRE
Istituzioni di Analisi Superiore (II
Mutuato con Analisi Matematica
modulo)
VI, nuovo ordinamento
Istituzioni di Geometria Superiore
Mutuato con Geometria V , nuovo
(II modulo)
ordinamento
Istituzioni di Fisica Matematica (II Docente: E. Laserra
modulo)
Istituzioni di Algebra Superiore (II Mutuato con Algebra III, nuovo
modulo)
ordinamento
Matematiche Complementari (II
modulo)
Logica Matematica (II modulo)
Storia delle Matematiche (II
modulo)
Analisi Funzionale (II modulo)
Teoria dell’Informazione (II
modulo)
Teoria delle Funzioni (II modulo)
Calcolo Numerico e
Programmazione I (II modulo)
Calcolo Numerico e
Programmazione II
Algebra Superiore (II modulo)
Geometria Superiore
Ricerca operativa (II modulo)
Mutuato con Teoria della
Computabilità I, nuovo ordinamento
Mutuato con Logica Matematica I,
nuovo ordinamento
Mutuato con Matematiche
Elementari da un piunto di vista
superiore, nuovo ordinamento
Mutuato con Analisi Funzionale II,
nuovo ordinamento
Mutuato con Metodi per il
Trattamento dell’Informazione,
nuovo ordinamento
Docente: V. Cafagna
Docente : M.R. Crisci
Mutuato con Analisi Numerica +
Calcolo Numerico II, nuovo
ordinamento
Docente: G: Vincenzi
Mutuato con Geometria VI, nuovo
ordinamento
Mutuato con l’analogo corso del
C.L. in Informatica
NORME DI PROPEDEUTICITÀ
Gli studenti dovranno attenersi alle seguenti propedeuticità:
ESAMI
PROPEDEUTICI PER
Algebra
Analisi Matematica I
Geometria I
Geometria II
Analisi Matematica II
Geometria II
Meccanica Razionale
Fisica Generale II
Meccanica Razionale
Istituzioni di Algebra Superiore
Istituzioni di Analisi Superiore
Istituzioni di Fisica Matematica
Istituzioni di Geometria Superiore
Fisica Generale I
Analisi Matematica II
Geometria II
Meccanica Razionale
Algebra
Analisi Matematica I
Geometria I
Analisi Matematica II
Geometria II
Istituzioni di Fisica Matematica
Tutti gli esami opzionali
Tutti gli esami opzionali eccetto
che per gli esami di
Calcolo
Numerico e Programmazione I,
Teoria dell’Informazione
ESAME DI LAUREA
L'esame di laurea comprenderà la discussione di una dissertazione scritta
e di una tesina orale su un argomento distinto.
Superato l'esame di laurea lo studente consegue il titolo di dottore in
matematica indipendentemente dall'indirizzo prescelto. L'indirizzo
seguito potrà essere indicato a richiesta dell'interessato nei certificati degli
studi rilasciati dalle università.
Per l’anno accademico 2003/2004 è previsto il seguente calendario:
Lezioni
Semestre
Primo
Secondo
Data di inizio
6 ottobre 2003
8 marzo 2004
Data di fine
18 gennaio 2004
31 maggio 2004
Data di inizio
2 febbraio 2004
9 giugno 2004
1 settembre 2004
Data di fine
5 marzo 2004
31 luglio 2004
30 settembre 2004
Esami
Sessione
Prima
Seconda
Terza
Il colloquio di lingua inglese si svolgerà tre volte l’anno, nei mesi di
giugno, novembre e febbraio, e potrà essere sostenuto solo dagli studenti
iscritti dal terzo anno in poi.
TUTORATO
Il tutorato si propone di contribuire all'orientamento degli studenti nel
corso degli studi, migliorando le condizioni di apprendimento e riducendo
i tassi di abbandono.
All'atto dell'iscrizione ciascuno studente viene affidato ad un tutore
secondo modalità precisate ogni anno sulla Guida dello Studente. Per
l'Anno Accademico 2003/2004 l'associazione studente-tutore è
determinata dal resto della divisione della matricola dello studente per 27
e dalla consultazione della seguente tabella.
TUTORE
RESTO
Cafagna V.
Canale A.
Capobianco G.
Caso L.
Cavaliere P.
Crisci M.R.
Delizia C.
Di Concilio A.
Di Gironimo P.
Di Nola A.
Esposito L.
Fedullo A.
Franciosi M.
Fusco-Girard M.
Gerla G.
Giorno V.
Laserra E.
Longobardi P.
Maj M.
Nicotera C.
Palladino F.
Sgambati L.
Sparano G.
Transirico M.
Vincenzi G.
Vinogradov A.
Vitolo A.
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Agli studenti il cui tutore è per qualche motivo indisponibile viene
effettuata una nuova assegnazione con modalità stabilite dal Presidente
del Consiglio di Corso di Laurea. Il tutore dovrà fornire informazioni sul
corso di laurea, seguire da vicino l'attività di studio dello studente
affidatogli, assisterlo nella elaborazione del piano di studi e nella scelta
della tesi di laurea.
Gli studenti sono invitati a relazionare al proprio tutore, almeno due volte
l'anno, sul proprio iter di studio.
Almeno una volta l'anno verrà discusso in Consiglio di Corso di Laurea
l'andamento del tutorato.
INSEGNAMENTI OPZIONALI
Istituzioni di logica matematica
Logica matematica
Teoria degli insiemi
Teoria dei modelli
Teoria della ricorsività
Algebra superiore
Algebra commutativa
Algebra computazionale
Algebra ed elementi di geometria
Algebra lineare
Istituzioni di algebra superiore
Matematica discreta
Teoria algebrica dei numeri
Teoria dei gruppi
Geometria algebrica
Geometria combinatoria
Geometria descrittiva
Geometria differenziale
Geometria superiore
Istituzioni di geometria superiore
Spazi analitici
Topologia
Topologia algebrica
Topologia differenziale
Didattica della matematica
Fondamenti della matematica
Matematiche complementari
Matematiche elementari da un punto di vista superiore
Storia delle matematiche
Storia dell'insegnamento della matematica
Analisi armonica
Analisi convessa
Analisi funzionale
Analisi non lineare
Analisi superiore
Calcolo delle variazioni
Equazioni differenziali
Istituzioni di analisi matematica
Istituzioni di analisi superiore
Matematica applicata Teoria dei numeri
Teoria delle funzioni
Teoria matematica dei controlli
Calcolo delle probabilità
Calcolo delle probabilità e statistica matematica
Filtraggio e controllo stocastico
Metodi matematici e statistici
Metodi probabilistici statistici e processi stocastici
Processi stocastici
Statistica matematica
Teoria dei giochi
Teoria dell'affidabilità
Teoria delle code
Teoria delle decisioni
Teoria dell'informazione
Equazioni differenziali della fisica matematica
Matematica applicata
Meccanica analitica
Meccanica del continuo
Meccanica razionale con elementi di meccanica statistica
Meccanica superiore
Metodi e modelli matematici per le applicazioni
Metodi geometrici della fisica matematica
Metodi matematici e statistici
Metodi matematici per l'ingegneria
Propagazione ondosa
Sistemi dinamici
Stabilità e controlli
Teorie relativistiche
Analisi numerica
Calcolo numerico
Calcolo parallelo
Calcolo numerico e programmazione
Calcolo numerico e programmazione II
Laboratorio di programmazione e calcolo
Matematica computazionale
Metodi di approssimazione
Metodi numerici per la grafica
Metodi numerici per l'ingegneria
Metodi numerici per l'ottimizzazione
Grafi e reti di flusso
Metodi e modelli per il supporto alle decisioni
Metodi e modelli per la logistica
Metodi e modelli per l'organizzazione e la gestione
Metodi e modelli per la pianificazione economica
Metodi e modelli per la pianificazione territoriale
Modelli di sistemi di produzione
Modelli di sistemi di servizio
Ottimizzazione
Ottimizzazione combinatoria
Programmazione matematica
Ricerca operativa
Tecniche di simulazione
Complementi di fisica generale
Didattica della fisica
Esperimentazioni di fisica
Fisica sperimentale
Fisica teorica
Laboratorio di fisica
Laboratorio di fisica generale
Preparazione di esperienze didattiche
Calcolatori elettronici
Fondamenti di informatica
Informatica generale
Informatica applicata
Informatica teorica
Laboratorio di informatica
Sistemi di elaborazione
Sistemi di elaborazione dell'informazione
PROGRAMMI DEL CORSO DI LAUREA
DI PRIMO LIVELLO IN MATEMATICA
(NUOVO ORDINAMENTO)
ALGEBRA I
Docente: M. MAJ
Obiettivi
Scopo di questo corso è di approfondire lo studio di
alcune notevoli
strutture algebriche, quali i
gruppi, gli anelli, gli spazi vettoriali.
Programma del corso
Strutture Algebriche: esempi, sottostrutture, congruenze, omomorfismi
tra strutture.
Gruppi : esempi, gruppi di permutazioni, gruppi di matrici, sottogruppi,
sottogruppo generato, congruenze in un gruppo e gruppo quoziente,
omomorfismi tra gruppi, gruppi ciclici, periodo di un elemento, prodotti
diretti.
Anelli: esempi, anelli di polinomi, sottoanelli ed ideali, anello
quoziente,omomorfismi, caratteristica, campo dei quozienti, anelli
fattoriali e principali, anelli euclidei.
Spazi Vettoriali: esempi, sottospazi, quozienti, omomorfismi, basi di uno
spazio vettoriale, dimensione, sottospazi supplementari, spazi vettoriali di
dimensione finita.
Testi consigliati
M. CURZIO, P. LONGOBARDI, M. MAJ, - Lezioni di Algebra Liguori Editore , Napoli, 1994
M. CURZIO, P. LONGOBARDI, M. MAJ, - Esercizi di Algebra – Una
raccolta di prove d’esame svolte - Liguori Editore , Napoli, 1995
ALGEBRA II
Docente: P. LONGOBARDI
Obiettivi
Scopo di questo corso è completare lo studio degli spazi vettoriali e
approfondire lo studio dei polinomi e della teoria dei campi. Vengono
inoltre illustrati risultati classici di Teoria di Galois sulla risolubilità per
radicali delle equazioni algebriche.
Programma del corso
Spazi vettoriali: richiami. Somme dirette di sottospazi. Struttura additiva
di uno spazio vettoriale e di un corpo
Polinomi : richiami sulle radici di un polinomio, radici semplici, radici
multiple, polinomi primitivi, polinomi su di un anello fattoriale. Teorema
della base di Hilbert.
Teoria dei Campi: elementi algebrici e trascendenti, estensioni
algebriche e trascendenti, campi algebricamente chiusi, campo di
spezzamento di un polinomio, campi finiti, estensioni separabili, campi
perfetti, estensioni normali.
Gruppi risolubili : definizione, esempi, proprietà fondamentali.
Teoria dei Galois: gruppo di Galois di un'estensione e di un polinomio,
teorema fondamentale della teoria di Galois, risolubilità per radicali di
un'equazione, criterio di Galois, teorema di Abel-Ruffini.
Testi consigliati:
M. CURZIO, P. LONGOBARDI, M. MAJ - Lezioni di algebra , Liguori ,
1994 (II ed. 1996)
N. JACOBSON - Basic Algebra I, II, Freeman, San Francisco, 1980.
Metodi di valutazione
Prova scritta e prova orale.
ALGEBRA III
Docente : M. MAJ
Obiettivi
Scopo di questo corso è di approfondire lo studio della teoria dei moduli
su di un anello unitario. Vengono inoltre illustrati risultati di teoria dei
numeri cardinali e ordinali e di teoria delle categorie.
Contenuti:
Numeri cardinali e ordinali.
Categorie e funtori.
Teoria dei moduli: esempi, somme e prodotti diretti di una famiglia di
moduli, moduli semplici, moduli fedeli, moduli periodici e aperiodici.
Moduli liberi, moduli proiettivi , iniettivi, divisibili. Moduli su di un
anello principale. Prodotto tensoriale.
Testi consigliati
M. CURZIO, P. LONGOBARDI, M: MAJ, - Lezioni dai Algebra Liguori Editore , Napoli, 1994
T.W. HUNGERFORT - Algebra - Springer-Verlag, Berlin 1973.
ALGEBRA IV
Docente: G. VINCENZI
Obiettivi
Questo corso è dedicato all’approfondimento dello studio degli anelli e
dei gruppi abeliani.
Contenuti
Teoria degli Anelli: Ideali primi ed ideali massimali. Decomposizione
primaria di un ideale. Nilradicale e radicale di Jacobson di un anello.
Operazioni con gli ideali. Estensioni e contrazioni.
Teoria dei Gruppi Abeliani: Struttura dei gruppi Abeliani finitamente
generati. Gruppi abeliani divisibili, e gruppi abeliani ridotti. Prodotto
tensoriale di gruppi abeliani. Generalizzazioni rilevanti dei gruppi
abeliani.
ANALISI FUNZIONALE I
6 CFU
SSD MAT/05
Obiettivi
Scopo del corso è lo studio dei problemi istituzionali dell’Analisi
Funzionale.
Contenuti :
Teoremi fondamentali di analisi lineare (Hahn-Banach, applicazione
aperta, uniforme limitatezza, grafico chiuso). Topologie deboli e spazi
convessi.
ANALISI FUNZIONALE II
3 CFU
SSD MAT/05
Obiettivi
Scopo del corso è lo studio dei problemi istituzionali dell’Analisi
Funzionale.
Contenuti
Spazi Lp
Spazi di Sobolev in dimensione uno.
ANALISI MATEMATICA I
Docente: M. TRANSIRICO
Obiettivi
Il corso di Analisi matematica I è dedicato essenzialmente allo studio
delle funzioni reali di una variabile reale e alla teoria dei limiti di tali
funzioni.
Gli obiettivi formativi del corso consistono nell’acquisizione dei risultati e
delle tecniche dimostrative, nonché nella capacità di utilizzare i relativi
strumenti di calcolo.
Programma del corso
1. I numeri reali
2. Le funzioni reali
3. I numeri complessi
4. Limiti di successioni
5. Limiti di funzioni e funzioni continue
6. Complementi ai limiti
Testi consigliati
P. MARCELLINI , C. SBORDONE - Analisi Matematica uno - Liguori
Editore
P. MARCELLINI , C. SBORDONE - Esercitazioni di Matematica I Liguori EDITORE
A. ALVINO, L. CARBONE , G. TROMBETTI - Esercitazioni di
Matematica I - Liguori Editore
M. TROISI - Analisi matematica I - Liguori Editore
D. GRECO, G. STAMPACCHIA - Esercitazioni di Matematica Volume
primo - Liguori Editore
ANALISI MATEMATICA II
Docente: M. TRANSIRICO
Obiettivi
Il corso di Analisi matematica II è dedicato essenzialmente alla teoria
della derivazione e dell’integrazione per funzioni reali di una variabile
reale, e allo studio delle serie numeriche.
Gli obiettivi formativi del corso consistono nell’acquisizione dei risultati
e delle tecniche dimostrative, nonché nella capacità di utilizzare gli
strumenti del calcolo differenziale e del calcolo integrale.
Programma del corso
1. Derivate
2. Applicazioni delle derivate. Studio di funzioni
3. Integrazione secondo Riemann
4. Integrali indefiniti
5. Formula di Taylor
6. Serie numeriche
Testi consigliati
P. MARCELLINI , C. SBORDONE - Analisi Matematica uno - Liguori
Editore
P. MARCELLINI , C. SBORDONE - Esercitazioni di Matematica I Liguori EDITORE
A. ALVINO, L. CARBONE , G. TROMBETTI - Esercitazioni di
Matematica I - Liguori Editore
M. TROISI - Analisi matematica I - Liguori Editore
D. GRECO, G. STAMPACCHIA - Esercitazioni di Matematica Volume
primo - Liguori Editore
ANALISI MATEMATICA III
Docente: L. SGAMBATI
Obiettivi
Il corso di Analisi Matematica III è dedicato allo studio delle successioni
e serie di funzioni, alla teoria delle funzioni di più variabili reali ed allo
studio delle equazioni differenziali. Relativamente a tali argomenti
vengono forniti i risultati fondamentali, le tecniche di dimostrazione e gli
strumenti di calcolo. Sono richieste solide basi della teoria delle funzioni
numeriche di una variabile reale, che è oggetto del corso di Analisi
Matematica I; si ritiene altresì indispensabile un’adeguata conoscenza dei
risultati e delle tecniche di calcolo tipiche dell’algebra lineare, che
rientrano nel programma di Geometria I.
Programma del corso
1. Successioni e serie di funzioni
2. Funzioni di più variabili reali
3. Equazioni differenziali ordinarie
4. Equazioni differenziali lineari
5. Curve ed integrali curvilinei
6. Forme differenziali lineari
Testi consigliati
N. FUSCO, P. MARCELLINI , C. SBORDONE - Analisi Matematica
due - Liguori Editore
P. MARCELLINI , C. SBORDONE - Esercitazioni di Matematica II Liguori EDITORE
ANALISI MATEMATICA IV
Docente: L. SGAMBATI
Obiettivi
Il corso di Analisi Matematica IV è dedicato agli integrali multipli, alla
teoria dell’integrazione secondo Lebesgue e alle funzioni implicite.
Relativamente a tali argomenti vengono forniti i risultati fondamentali, le
tecniche di dimostrazione e gli strumenti di calcolo. Sono richieste solide
basi della teoria delle funzioni numeriche di una variabile reale, che è
oggetto del corso di Analisi Matematica I; degli argomenti trattati nel
corso di Analisi Matematica III; si ritiene altresì indispensabile
un’adeguata conoscenza dei risultati e delle tecniche di calcolo tipiche
dell’algebra lineare, che rientrano nel programma di Geometria I.
Programma del corso
1. Integrali multipli
2. Misura di Lebesgue
3. Integrale di Lebesgue
4.
5.
Cenni su superfici ed integrali superficiali
Funzioni implicite
Testi consigliati
N. FUSCO, P. MARCELLINI , C. SBORDONE - Analisi Matematica
due - Liguori Editore
P. MARCELLINI , C. SBORDONE - Esercitazioni di Matematica II Liguori EDITORE
ANALISI MATEMATICA V
Docente: A. Vitolo
Programma
TEORIA
Rappresentazioni e algebra dei numeri complessi. Funzioni olomorfe.
Condizioni di Cauchy – Riemann.
Serie di potenze. La funzione esponenziale. Le funzioni trigonometriche.
Funzioni polidrome. La funzione logaritmo e la funzione potenza.
Integrale curvilineo di una funzione di variabile complessa. Teorema
integrale di Cauchy. Derivazione sotto il segno di integrale.
Formula integrale di Cauchy e applicazioni. Teoremi del “massimo
modulo” e della “media”. Torema di Morera. Serie di funzioni analitiche
e Teorema di Weierstrass. Teorema di Liouville e Teorema fondamentale
dell’algebra.
Sviluppo in serie di Taylor. Zeri delle funzioni olomorfe. Sviluppo in
serie di Laurent in una corona circolare. Classificazione delle singolarità
isolate. Comportamento di una funzione intorno alle singolarità isolate.
Teoria dei residui. Indicatore logaritmico. Applicazione al calcolo di
integrali definiti.
Funzione Zeta di Riemann. Funzioni Beta e Gamma. Funzioni speciali e
applicazioni.
ESERCITAZIONI
Calcolo di integrali definiti mediante i teoremi dei residui e di Jordan.
Testi consigliati:
[1]
D.GRECO, Complementi di Analisi Matematica, Liguori (NA).
[2]
W.RUDIN, Analisi reale e complessa, Boringhieri (FI).
ANALISI MATEMATICA VI
Docente: A: VITOLO
Programma
TEORIA
1. Teoria della misura e integrazione astratta.
Algebre e σ - algebre. Misure. Costruzione di misure da misure esterne e
di misure esterne da funzioni di insieme. La misura di Lebesgue.
Spazi di misura. Integrale. Teoremi di passaggio al limite sotto il segno di
integrale.
Confronto fra vari tipi di convergenza: quasi ovunque, quasi uniforme, in
media di ordine p.
p
Spazi L . Esponenti coniugati e disuguaglianza di Hölder. Inclusione fra
p
p
spazi L . Teorema di Fisher – Riesz. Densità di C0 in L . Convoluzione.
p
p
∞
Mollificatori. Densità di C0 in L . Continuità della traslazione in L .
1. Spazi di Hilbert.
Forme bilineari simmetriche. Prodotti scalari. Spazi euclidei.
Disuguaglianza di Cauchy - Schwarz. Regola del parallelogramma.
Identità di polarizzazione.
n
n 2
2
Spazi di Hilbert. Modelli: R , C , l , L . Proiezioni e decomposizione in
sottospazi ortogonali.
Funzionali lineari e continui. Teorema di rappresentazione di Riesz.
Sistemi
ortonormali.
Completezza.
Coefficienti
di
Fourier.
Disuguaglianza di Bessel. Separabilità e criteri di completezza: unicità dei
coefficienti di Fourier, convergenza della serie di Fourier alla funzione
2
2
generatrice, identità di Parseval. Isomorfismo fra l e L .
2. Serie di Fourier.
Analisi e sintesi di Fourier dei segnali periodici. Condizioni per la
convergenza uniforme. Integrazione termine a termine della serie di
Fourier. Applicazione al calcolo della somma di serie numeriche.
2
Completezza del sistema trigonometrico in L (-π,π).
3. Trasformata di Fourier.
1
Definizione e proprietà della trasformata di Fourier in L . Teoremi di
1
2
unicità e inversione in L . Estensione della trasformata di Fourier a L .
Teorema di Plancherel.
ESERCITAZIONI
- Spettro di una funzione periodica.
- Calcolo di trasformate di Fourier.
Testi consigliati:
[1]
D.GRECO, Complementi di Analisi Matematica, Liguori (NA).
[2]
G.GIUSTI, Analisi Matematica II, Boringhieri (FI).
[3]
H.BREZIS, Analisi Funzionale, Liguori (NA).
[4]
A.TESEI, Istituzioni di Analisi Superiore, Boringhieri (FI).
[5]
W.RUDIN, Analisi reale e complessa, Boringhieri (FI).
ANALISI NUMERICA
Docente: E. RUSSO
Obiettivi
Il corso è finalizzato a mettere lo studente in grado di sviluppare software
matematico efficiente, sia sequenziale che parallelo. Particolare
attenzione sarà rivolta alle metodologie di progettazione di algoritmi
numerici efficienti ed ai metodi numerici per equazioni alle derivate
parziali.
Parte integrante del corso sono le esercitazioni in laboratorio, nelle quali
sarà sviluppato software numerico parallelo in ambiente MPI.
Programma
Risoluzione numerica di equazioni a derivate parziali.
Fondamenti di teoria. Sistemi di equazioni a derivate parziali lineari del II
ordine. Equazioni paraboliche. Metodi alle differenze finite. Schemi
espliciti ed impliciti. Stima degli errori. Stabilità. Convergenza. Teorema
di Lax. Metodi delle linee. Equazioni di tipo ellittico. Metodi alle
differenza finite. Teorema di unicità della soluzione dello schema. Stima
dell'errore. Convergenza. Metodi risolutivi di tipo iterativo per il sistema
lineare dello schema. Metodi di Jacobi. Metodo di Liebman.
Convergenza.
Calcolo parallelo. Architetture parallele. Indici di valutazione di un
algoritmo parallelo. Parallelismo SIMD e MIMD. Il sistema MPI. Metodi
paralleli WR per la risoluzione di sistemi di equazioni differenziali
ordinarie.
Testi consigliati
J.B.Lambert, Computational methods in ordinary differential equations,
J.Wiley Sons
E.Isaacson, H.Keller, Analysis of numerical methods, J.Wiley Sons
V.Comincioli, Analisi numerica, McGraw Hill
MPI Manuale
Metodi di valutazione
Prova orale preceduta da una discussione sugli elaborati sviluppati
durante il corso o, in assenza di questi, da una prova al calcolatore.
CALCOLO DELLE PROBABILITA’ E STATISTICA
Docente : A. DE CRESCENZO
Programma del corso
Probabilità
Spazio di probabilità. Probabilità condizionata. Indipendenza. Primi
teoremi della probabilità.
Variabili aleatorie
Variabili aleatorie. Funzioni di ripartizione e relative proprietà. Variabili
aleatorie discrete ed assolutamente continue. Valore atteso, varianza,
momenti. Principali distribuzioni di probabilità. Vettori aleatori. Funzioni
di ripartizione multiple. Indipendenza. Covarianza e correlazione.
Teorema centrale di convergenza
Funzione generatrice dei momenti. Funzione caratteristica Disuguaglianza
di Chebyshev. Criteri di convergenza per successioni di variabili
aleatorie. Legge dei grandi numeri. Teorema centrale di convergenza.
Processi stocastici
Generalità. Processi di Marcov. Processo di Poisson. Catene di Markov.
Processo di moto Browniano. Applicazioni.
Testi consigliati
DALL'AGLIO G. (2000) Calcolo delle Probabilità. II edizione.
Zanichelli.
ROSS G. (1996) Stochastic Processes. II edizione. John Wiley & Sons.
CALCOLO NUMERICO I
Docente : M. R. CRISCI
Obiettivi
Introduzione ai metodi numerici, alle metodologie di progettazione di
algoritmi efficienti e all'uso di opportuni ambienti di calcolo numerico e
simbolico per la risoluzione di problemi di calcolo scientifico.
Parte integrante del corso sono le esercitazioni in laboratorio, nelle quali
saranno utilizzati i metodi su problemi realistici e con l'aiuto di esempi e
controesempi saranno individuati i principali vantaggi e punti deboli dei
metodi presentati.
Programma
Integrazione numerica: Formule di Newton - Cotes e di Gauss. Integratori
automatici basati su schemi adattativi.
Autovalori di matrici. Metodi iterativi e metodi basati su trasformazioni di
similitudine.
Sistemi di equazioni non lineari: Metodi iterativi.
Sistema di calcolo simbolico Mathematica.
Sviluppo di codici Matlab relativi ai principali algoritmi trattati.
Testi consigliati
V. Comincioli - Analisi Numerica - Ed. Mc Graw
CALCOLO NUMERICO II
Docente: E. RUSSO
Obiettivi:
Il corso è finalizzato a mettere lo studente in grado di sviluppare software
matematico efficiente, sia sequenziale che parallelo. Particolare
attenzione sarà rivolta ai metodi numerici per equazioni differenziali
ordinarie ed alle metodologie di progettazione di algoritmi numerici
efficienti.
Parte integrante del corso sono le esercitazioni in laboratorio, nelle quali
sarà sviluppato software numerico parallelo in ambiente MPI su problemi
realistici.
Programma:
Risoluzione numerica di equazioni differenziali ordinarie.
Metodi di approssimazione di tipo analitico. Metodi lineari multistep.
Metodi predictor-corrector. Metodi non lineari a un passo. Metodi RungeKutta. Metodi multistep a passo variabile. Ordine. Stima degli errori.
Consistenza. Convergenza. Zero-stabilità. Teoria della debole stabilità.
Stabilità non lineare. Problemi stiff. Metodi BDF.
Calcolo parallelo. Architetture parallele. Indici di valutazione di un
algoritmo parallelo. Parallelismo SIMD e MIMD. Il sistema MPI. Metodi
paralleli WR per la risoluzione di sistemi di equazioni differenziali
ordinarie.
Testi consigliati:
J.B.Lambert, Computational methods in ordinary differential equations,
J.Wiley Sons
E.Isaacson, H.Keller, Analysis of numerical methods, J.Wiley Sons
V.Comincioli, Analisi numerica, McGraw Hill
MPI Manuale
Metodi di valutazione:
Prova orale preceduta da una discussione sugli elaborati sviluppati
durante il corso o, in assenza di questi, da una prova al calcolatore.
FISICA GENERALE I
Docenti: A. Cucolo, M. Fusco-Girard
Contenuti:
Grandezze fisiche e loro misura. Sistemi di unità. Algebra dei vettori.
Moto in una dimensione: velocità ed
accelerazione scalari. Moto nel piano e nello spazio. Forze. I principi
della dinamica. Energia cinetica. Lavoro. Forze conservative.
Conservazione dell’energia meccanica. Sistemi di punti materiali.
Gravitazione. Oscillazioni. Temperatura e calore. Primo principio della
termodinamica. Secondo principio della termodinamica. Concetto di
entropia.
FISICA GENERALE II
Docente: M. Fusco-Girard
Contenuti:
Carica elettrica e fenomeni elettrostatici elementari. Campo elettrico e
sue proprietà. Conduttori ed isolanti, capacità. Correnti elettriche
continue, leggi di Ohm, potenza elettrica ed effetto Joule, circuiti
elementari. Campo magnetico e correnti elettriche. Forze magnetiche su
correnti. Induzione elettromagnetica. Circuiti RL ed RLC. Correnti
alternate. Equazioni di Maxwell. Onde elettromagnetiche. Ottica.
Relatività ristretta. Cenni di fisica moderna.
FISICA MATEMATICA
Docente: E. LASERRA
Programma del corso
Meccanica Analitica
Equazioni del moto di un arbitrario sistema di particelle: Sistemi
olonomi. Equazione simbolica della meccanica. Principio dei lavori
virtuali. Equazioni di Lagrange. Cenni sui sistemi anolonomi. Equazioni
di Appel.
Equazioni del moto in un campo potenziale: Equazioni di Lagrange per
forze potenziali. Equazioni canoniche di Hamilton. Equazioni di Routh.
Parentesi di Poisson.
Principi variazionali: Principio di Hamilton. Principio di HamiltonHelmoltz. Principio di Maupertuis-Lagrange. Invarianti integrali.
Teorema di Liouville.
Trasformazioni canoniche ed equazione di hamilton-jacobi.
Testi consigliati
G. CARICATO - Fondamenti di meccanica newtoniana - Cisu
M. FABRIZIO - La Meccanica Razionale e i suoi metodi matematici .
F.STOPPELLI - Appunti di meccanica razionale - Liguori.
FONDAMENTI DI INFORMATICA E LABORATORIO
Docente : D. PARENTE
Obiettivi
Comprensione della struttura di un calcolatore, apprenndimento dei
principi base dei Sistemi Operativi,
Acquisizione delle tecniche basilari per la progettazione ed
implementazione di programmi nel linguaggio
ANSI-C con utilizzo di semplici strutture dati.
Contenuti
Introduzione alla struttura di un computer, Hardware e Software,
introduzione ai Sistemi Operativi, introduzione alla programmazione nel
linguaggio ANSI-C, concetti fondamentali per lo sviluppo software,
tecniche fondamentali per
la scrittura, compilazione ed esecuzione di semplici programmi in C.
GEOMETRIA I
Docente: G. SPARANO
Obiettivi:
Il corso di Geometria I è dedicato allo studio degli spazi vettoriali, dei
sistemi di equazioni lineari e, attraverso le matrici, degli strumenti di
calcolo dell’algebra lineare. Relativamente a tali argomenti vengono
forniti i risultati fondamentali, le tecniche di dimostrazione e gli strumenti
di calcolo.
Programma del corso:
1. Matrici e determinanti
2. Sistemi di equazioni lineari
3. Spazi vettoriali
4. Applicazioni lineari
5. Spazi vettoriali euclidei
Testi consigliati:
R. ESPOSITO, A. RUSSO, Lezioni di geometria I
S. LANG, Algebra lineare, Boringhieri
E. SERNESI, Geometria 1, Boringhieri
GEOMETRIA II
Docente: G. SPARANO
Obiettivi:
Il corso di Geometria II è dedicato allo studio degli spazi vettoriali
euclidei e alla geometria affine ed euclidea. Relativamente a tali
argomenti vengono forniti i risultati fondamentali, le tecniche di
dimostrazione e gli strumenti di calcolo. Sono richieste solide basi degli
argomenti trattati nel corso di Geometria I, in particolare della teoria degli
spazi vettoriali e delle tecniche di calcolo dell’algebra lineare.
Programma del corso
1. Spazi vettoriali euclidei
2. Spazi affini
3. Spazi affini euclidei
4. Iperquadriche
Testi consigliati:
R. ESPOSITO, A. RUSSO, Lezioni di geometria I
E. SERNESI, Geometria 1, Boringhieri
LABORATORIO DI PROGRAMMAZIONE E CALCOLO
Docente: G. CAPOBIANCO
Obiettivi:
Introduzione ai metodi numerici, alle metodologie di progettazione di
algoritmi efficienti e all'uso di opportuni ambienti di calcolo numerico e
simbolico per la risoluzione di problemi di calcolo scientifico.
Parte integrante del corso sono le esercitazioni in laboratorio, nelle quali
saranno utilizzati i metodi su problemi realistici e con l'aiuto di esempi e
controesempi saranno individuati i principali vantaggi e punti deboli dei
metodi presentati.
Contenuti
Dal problema all'algoritmo. Concetto di algoritmo e requisiti.
Programmazione strutturata. La macchina di von Neumann.
Linguaggio di programmazione Matlab.
Nozioni di analisi degli errori. Rappresentazione dei numeri in un
calcolatore. Aritmetica floating - point.
Sistemi di equazioni lineari: Metodi diretti ed iterativi.
Approssimazione: Interpolazione polinomiale e con funzioni spline.
Approssimazione nel senso dei minimi quadrati.
Sviluppo di codici relativi ai principali algoritmi trattati.
LOGICA MATEMATICA I
Docente: A. DI NOLA
Obiettivi
Scopo di questo corso è di affrontare lo studio della logica mediante i
sistemi formali.
Contenuti
Elementi di Calcolo Preposizionale e Predicativo e loro teoremi di
deduzione e completezza.
LOGICA MATEMATICA II
Docente: A. DI NOLA
Obiettivi :
Scopo di questo corso è di affrontare lo studio delle proprieta’ delle teorie
del primo ordine e introdurre lo studente a logiche non classiche.
Contenuti :
Teorie del primo ordine e loro proprieta’. Teorie del primo ordine con
identita’. Forme Normali Prenesse. Categoricita’ di teorie. Elementi di
Logica Polivalente.
MATEMATICHE COMPLEMENTARI I
Docente: F. PALLADINO
Obiettivi:
Il corso si occupa di "filosofia della matematica" esaminando criticamente
le nozioni-base della matematica (quali quelle di punto, retta, infinito,
insieme, dimostrazione, algoritmo, probabilità) sia da un punto di vista
epistemologico che storico. Lo scopo è di ridurre il divario tra cultura
umanistica e quella scientifica e di aumentare lo spirito critico e la
consapevolezza di chi dovrà svolgere il lavoro di matematico.
Contenuti:
La Scuola pitagorica e sua crisi, gli Elementi di
Euclide, idealizzazione degli enti matematici.
Cartesio e la crisi dell'approccio sintetico. Le
geometrie non euclidee. La teoria degli insiemi.
L'aritmetizzazione della geometria e dell'analisi.
Infinito attuale ed infinito potenziale. Crisi della
teoria degli insiemi, le antinomie. Il metodo
assiomatico, il punto di vista fondazionale e quello
strutturalista. Il fallimento del programma di
Hilbert. I teoremi di Goedel. La probabilità, punto
di vista soggettivista, frequentista, combinatorio e
classico.
MATEMATICHE ELEMENTARI DA UUN PUNTO DI VISTA
SUPERIORE
Docente: F. PALLADINO
Obiettivi:
Il corso è finalizzato alla trattazione di qurestioni matematiche
elementari/fondaamentali mediante l’applicazione di più avaanzate ee
recenti nozioni matematiche. Il senso e il titolo originario del corso
traggono origine da F.Klein che, neella seconda metà dell’Ottocento,
corredò il suo insegnamento aa riguardo con una serie di volumi.
Contenuti:
I cisiddetti “Problemi classici dell’antichità”. Algoritmi numerici “storici”
e applicazioni informatiche.
MATEMATICA DI BASE
Docente: M. MAJ
Obiettivi:
Scopo di questo corso è di introdurre lo studente al
linguaggio
matematico,
abituandolo
alla
formulazione astratta dei problemi ed al
ragionamento rigoroso.
Contenuti:
1. Teoria ingenua degli insiemi.
2. Numeri naturali, principio d'induzione.
3. Elementi di calcolo combinatorio.
4. Numeri interi, congruenze.
5. Cardinalità di insiemi, insiemi finiti ed infiniti.
6. Strutture algebriche : prime definizioni ed esempi.
Testi consigliati
M. CURZIO, P. LONGOBARDI, M. MAJ, - Lezioni di Algebra Liguori Editore , Napoli, 1994
M. CURZIO, P. LONGOBARDI, M. MAJ, - Esercizi di Algebra – Una
raccolta di prove d’esame svolte - Liguori Editore , Napoli, 1995
SEMIGRUPPI LIBERI E TEORIA DEI CODICI
Docente: P: LONGOBARDI
Obiettivi
Scopo del corso è lo studio dei semigruppi e dei monoidi liberi, con
particolare riferimento a proprietà delle parole su un alfabeto, e di
elementi della teoria generale dei codici.
Contenuti
Generaliità sui semigruppi. Il semigruppo delle relazioni in un insieme.
Sottosemigruppi (sottomonoidi), congruenze, quozienti, omomorfismi.
Semigruppi ciclici. Il semigruppo sintattico.
Il semigruppo (monoide) delle parole su un insieme. Semigruppi
(monoidi) liberi. Presentazioni dei semigruppi (monoidi) Il monoide
biciclico.
Parole coniugate. Parole infinite. Le parole infinite di Thue-Morse. Parole
infinite libere da quadrati. Parole di Lyndon.
Generalità sui codici.. Proprietà combinatorie dei codici. Massimalità e
completezza. Famiglie di codici e di sottomonoidi di un semigruppo
libero.
Testi consigliati
J. BERSTEL ˆ D. PERRIN ˆ Theory of Codes , Academic Press, London ,
1985.
J. M. HOWIE ˆ An Introduction to Semigroup Theory , Academic Press,
London , 1976.
G. LALLEMENT ˆ Semigroups and Combinatorial Properties , Wiley ,
New York, 1979 .
M. LOTHAIRE ˆ Combinatorics on Words , Addison-Wesley , Reading,
1983 .
Metodi di valutazione
Prova orale.
STORIA DELLE MATEMATICHE
Docente: F. Palladino
Obiettivi
Il corso è finalizzato alla trattazione di questioni di storia delle scienze
matematiche, studiate dalle fonti primarie, avendo cura di mettere in
rilievo le attinenze con le moderne nozioni e idee della matematica.
Contenuti:
Gli Elementi di Euclide. Profilo storico. Studio dei seguenti capitoli
(libri) con relative proposizioni particolari. Libro I: 1, 2, 4, 5, 9, 16, 17,
27, 28, 29, 43, 47; Libro II: 1,2,3,4,5,6,7,9; Libro V: 1,2,3,4,5,6,7; Libro
VI: 1,3,8,13,14,16,23; Libro VII: 1,2; Libro IX:20, 36.
L’Algebra del Cinquecento e l’Algebra di Bombelli: Prefazione,
Analisi dell’opera, Libro I: Radice quadrata e Radice cubica, rispettivi
algoritmi di approssimazione; Libro II: equazioni di primo grado; Libro
IV: Costruzioni geometriche.
La “Formula di Cardano” per la risoluzione delle equazioni algebriche
di terzo grado, il caso irriducibile.
TEORIA DELLA COMPUTABILITÀ I
Docente: G: GERLA
Obiettivi
Il corso mira a definire una teoria astratta dei calcolatori e della
computabilità. In particolare ci si soffermerà sulle cose che un calcolatore
non potrà mai fare (teoremi limitativi). Lo scopo è di aumentare lo spirito
critico e la consapevolezza per quanto riguarda le potenzialità ed i limiti
dei moderni calcolatori.
Contenuti
Algoritmi e macchine. Macchine a memoria finita, gli automi. Cose che
un automa finito non può fare. Automi digitali, reti sequenziali, reti
combinatorie, calcolo proposizionale, porte logiche. Macchine a memoria
infinita, macchine a registri, funzioni ricorsive, Tesi di Church.
Decidibilità. Cose che una macchina a memoria infinita non può fare, il
teorema della fermata, il teorema di Rice. Sistemi di riscrittura, calcolo
simbolico. Il programma Mathematica
Propedeucità.
E’ opportuno che si siano superati gli esami del primo anno e che si
conosca almeno un linguaggio di programmazione.
TEORIA DELLA COMPUTABILITÀ II
Docente: G. GERLA
Obiettivi
Il corso è rivolto allo studio di macchine che ragionano, che apprendono,
che si evolvono, che hanno comportamenti non deterministi, che trattano
informazioni vaghe o incerte.
Contenuti
Complessità, reti neurali, sistemi inferenziali, logica fuzzy, controllo
fuzzy, algoritmi genetici, macchine probabilistiche, macchine
quantistiche.
Il programma Mathematica.
TEORIA DEI NUMERI
Docente: P: LONGOBARDI
Obiettivi
Scopo del corso è lo studio di proprietà classiche dei numeri interi.
Saranno inoltre illustrati esempi e applicazioni, e verrà fornito qualche
cenno storico.
Contenuti
Richiami sulla divisibilita’ nell'insieme dei numeri naturali e dei numeri
interi. Distribuzione dei numeri primi, primi di Fermat, primi di
Mersenne. Equazioni diofantine. Richiami sulle congruenze nell'insieme
dei numeri interi. Congruenze lineari, sistemi. Il teorema di Lagrange.
Pseudoprimi e numeri di Carmichael. Radici primitive. Funzioni
aritmetiche. Numeri perfetti. Residui quadratici e teorema di reciprocità.
Somme di quadrati. L'equazione pitagorica. Osservazioni sull'Ultimo
teorema di Fermat. Elementi di crittografia.
Testi consigliati
G. A. JONES ˆ J. M. JONES ˆ Elementary Number Theory , Springer ,
1998 (rist. 2003)
Metodi di valutazione
Prova orale.
TEORIA DELL’INFORMAZIONE
Docente: V. GIORNO
Obiettivi:
Il corso si prefige di fornire gli elementi di base per la modellizzazione di
un sistema di comunicazione unidimensionale in cui l'informazione è
trasmessa dalla sorgente alla destinazione attraverso un canale di
trasmissione generalmente soggetto a rumore aleatorio.
Contenuti:
Descrizione di un sistema di comunicazione unidimensionale.
Misure di informazione: Autoinformazione e mutua informazione.
Entropia di una variabile aleatoria. Entropia congiunta e condizionata.
Mutua informazione media. Entropia di vettori aleatori. Mutua
informazione media di vettori aleatori. Funzioni convesse e
disuguaglianza di Jensen. Teorema di elaborazione dei dati.
Sorgenti di informazione: Sorgenti discrete stazionarie senza memoria.
Teoremi di codifica in assenza di rumore sul canale. Algoritmo di
Huffman. Sorgenti di informazione discrete con memoria.
Canali: Canali finiti stazionari senza memoria. Capacità informazionale e
sua valutazione. Criteri di decodifica. Codifica in presenza di rumore sul
canale. Teoremi di codifica di Shannon.
Codici correttori d'errore: Codici lineari e di Hamming.
TEORIA DELLE FUNZIONI
Docente: V. CAFAGNA
Contenuti:
Richiami di analisi di Fourier
Trasformata di Fourier a finestra
Basi ortogonali dello spazio di Hilbert
Grani di Gabor
Ondine.
Pacchetti di ondine.
Teoria generale dei frames.
Calcolo differenziale sullo spazio di Hilbert: derivate di Fre’chet e di
Gateaux.
Mappe di Fredholm.
Teorema della funzione inversa e teorema del rango.
Grado di Smale per mappe di Fredholm.
Singolarità.
Applicazioni alla teoria della distorsione non lineare e alla teoria della
visione.
CORSO DI LAUREA SPECIALISTICA IN MATEMATICA
(NUOVO ORDINAMENTO)
PROGRAMMI DEGLI INSEGNAMENTI ATTIVATI NELL’ANNO
2003-2004
ALGEBRA III
6 CFU
SSD MAT/02
Obiettivi
Scopo di questo corso è di approfondire lo studio della teoria dei moduli
su di un anello unitario. Vengono inoltre illustrati risultati di teoria dei
numeri cardinali e ordinali e di teoria delle categorie.
Contenuti:
Numeri cardinali e ordinali.
Categorie e funtori.
Teoria dei moduli: esempi, somme e prodotti diretti di una famiglia di
moduli, moduli semplici, moduli fedeli, moduli periodici e aperiodici.
Moduli liberi, moduli proiettivi , iniettivi, divisibili. Moduli su di un
anello principale. Prodotto tensoriale.
ALGEBRA IV
6 CFU
SSD MAT/02
Obiettivi
Questo corso e’ dedicato all’approfondimento dello studio degli anelli e
dei gruppi abeliani.
Contenuti :
Teoria degli Anelli: Ideali primi ed ideali massimali. Decomposizione
primaria di un ideale. Nilradicale e radicale di Jacobson di un anello.
Operazioni con gli ideali. Estensioni e contrazioni.
Teoria dei Gruppi Abeliani: Struttura dei gruppi Abeliani finitamente
generati. Gruppi abeliani divisibili, e gruppi abeliani ridotti. Prodotto
tensoriale di gruppi abeliani. Generalizzazioni rilevanti dei gruppi
abeliani.
ANALISI FUNZIONALE I
6 CFU
SSD MAT/05
Obiettivi
Scopo del corso è lo studio dei problemi istituzionali dell’Analisi
Funzionale.
Contenuti
Teoremi fondamentali di analisi lineare (Hahn-Banach, applicazione
aperta, uniforme limitatezza, grafico chiuso).
Topologie deboli e spazi convessi.
ANALISI FUNZIONALE II
3 CFU
SSD MAT/05
Obiettivi
Scopo del corso è lo studio dei problemi istituzionali dell’Analisi
Funzionale.
Contenuti
Spazi Lp
Spazi di Sobolev in dimensione uno.
ANALISI MATEMATICA V
6 CFU
SSD MAT/05
Obiettivi:
Il corso di Analisi Matematica V è dedicato alla teoria delle funzioni di
variabile complessa, che ha relazioni con pressoché tutti i settori della
matematica e si propone di fornire i risultati e le tecniche dimostrative
della teoria, nonché le prospettive di applicazione a tematiche di livello
più avanzato. E’ strutturato in modo da richiedere una quantità minima di
preliminari e può essere seguito agevolmente da studenti che hanno
familiarità con i concetti di limite, continuità, derivata e integrale delle
funzioni di una variabile reale, nonché di successione e serie numerica,
sviluppati nei corsi di Analisi Matematica I e II. Fra le implicazioni nei
vari settori della matematica, si segnalano in particolare i riferimenti
all’Analisi Armonica (principio del massimo, problemi ai limiti per
l’operatore di Laplace, …) e alla Teoria Analitica dei Numeri (serie di
Dirichlet, ζ di Riemann, …).
Contenuti
1. Rappresentazioni del piano complesso.
2. Funzioni olomorfe e teorema integrale di Cauchy.
3. Formula integrale di Cauchy e applicazioni.
4. Serie di funzioni in campo complesso.
5. Serie di Taylor e zeri delle funzioni olomorfe.
6. Serie di Laurent e classificazione delle singolarità isolate.
7. Teoria dei residui e principio dell’argomento.
8. Funzioni speciali, con particolare riguardo alla Γ di Eulero e alle
funzioni di Bessel.
9. Serie di Dirichlet e ζ di Riemann.
ANALISI MATEMATICA VI
6 CFU
SSD MAT/05
Obiettivi
p
Il corso di Analisi Matematica VI è dedicato agli spazi L , previa
trattazione generale della teoria della misura e dell’integrazione,
evidenziandone la struttura di spazi di Banach, agli spazi di Hilbert, che
consentono di generalizzare al caso infinito-dimensionale alcune ben note
tecniche degli spazi euclidei di dimensione finita, e all’analisi di Fourier
sia in ambito discreto (serie) che nel caso continuo (trasformate), di
fondamentale importanza in molti settori applicativi fra i quali la teoria
dei segnali. L’obiettivo è fornire risultati, tecniche dimostrative e metodi
di calcolo. Per la comprensione degli argomenti del corso è richiesta la
familiarità con i concetti di limite, continuità, derivate e integrali delle
funzioni di una variabile reale, di successione e serie numeriche (Analisi
Matematica I e II), nonché di spazio vettoriale e applicazione lineare
(Geometria I).
Contenuti
1. Spazi di Banach di funzioni limitate e di funzioni continue.
2. Teoria della misura.
3. Integrazione in spazi di misura.
P
4. Spazi L : disuguaglianza di Holder, completezza, approssimazione
con funzioni regolari.
5. Spazi di Hilbert: decomposizione ortogonale, rappresentazione delle
forme lineari, sistemi ortonormali, modelli ed esempi in dimensione
infinita.
6. Funzioni periodiche e integrale di Riemann.
7. Serie di Fourier: convergenza puntuale, uniforme, integrazione
termine a termine.
1
8. Trasformata di Fourier in L : proprietà formali ed effetto
regolarizzante.
9. Formula di inversione della trasformata di Fourier e applicazione alle
equazioni differenziali.
2
10. Trasformata di Fourier in L e teorema di Plancherel.
CALCOLO NUMERICO II
Docente: E. RUSSO
Obiettivi:
Il corso è finalizzato a mettere lo studente in grado di sviluppare software
matematico efficiente, sia sequenziale che parallelo. Particolare
attenzione sarà rivolta ai metodi numerici per equazioni differenziali
ordinarie ed alle metodologie di progettazione di algoritmi numerici
efficienti.
Parte integrante del corso sono le esercitazioni in laboratorio, nelle quali
sarà sviluppato software numerico parallelo in ambiente MPI su problemi
realistici.
Programma:
Risoluzione numerica di equazioni differenziali ordinarie.
Metodi di approssimazione di tipo analitico. Metodi lineari multistep.
Metodi predictor-corrector. Metodi non lineari a un passo. Metodi RungeKutta. Metodi multistep a passo variabile. Ordine. Stima degli errori.
Consistenza. Convergenza. Zero-stabilità. Teoria della debole stabilità.
Stabilità non lineare. Problemi stiff. Metodi BDF.
Calcolo parallelo. Architetture parallele. Indici di valutazione di un
algoritmo parallelo. Parallelismo SIMD e MIMD. Il sistema MPI. Metodi
paralleli WR per la risoluzione di sistemi di equazioni differenziali
ordinarie.
Testi consigliati:
J.B.Lambert, Computational methods in ordinary differential equations,
J.Wiley Sons
E.Isaacson, H.Keller, Analysis of numerical methods, J.Wiley Sons
V.Comincioli, Analisi numerica, McGraw Hill
MPI Manuale
Metodi di valutazione:
Prova orale preceduta da una discussione sugli elaborati sviluppati
durante il corso o, in assenza di questi, da una prova al calcolatore.
EQUAZIONI DIFFERENZIALI
6 CFU
SSD MAT/05
Obiettivi
Il corso di Equazioni differenziali è dedicato allo studio in senso classico
delle equazioni differenziali alle derivate parziali lineari di tipo ellittico
del secondo ordine. Gli obiettivi formativi del corso consistono
nell’acquisizione di alcuni risultati, di certe tecniche dimostrative e dei
possibili sviluppi di tale teoria.
Contenuti
1. L’equazione di Laplace
2. Il principio classico del massimo per operatori differenziali lineari
ellittici del secondo ordine
3. L’equazione di Poisson
4. Soluzioni classiche di equazioni differenziali lineari ellittiche del
secondo ordine
LOGICA MATEMATICA II
6 CFU
SSD MAT/01
Obiettivi
Scopo di questo corso è di affrontare lo studio delle proprietà delle teorie
del primo ordine e introdurre lo studente a logiche non classiche.
Contenuti
Teorie del primo ordine e loro proprieta’. Teorie del primo ordine con
identita’. Forme Normali Prenesse. Categoricita’ di teorie. Elementi di
Logica Polivalente.
STORIA DELLE MATEMATICHE
6 CFU
SSD MAT/04
Obiettivi
Il corso è finalizzato alla trattazione di questioni di storia delle scienze
matematiche, studiate dalle fonti primarie, avendo cura di mettere in
rilievo le attinenze con le moderne nozioni e idee della matematica.
Contenuti
Gli Elementi di Euclide. L’ Algebra di Bombelli. La scienza del moto di
Galilei. La Geometria di Cartesio. Il Calcolo infinitesimale. Elementi di
Storia dell’Informatica.
PROGRAMMI DEL CORSO DI LAUREA IN MATEMATICA
(VECCHIO ORDINAMENTO)
ALGEBRA SUPERIORE
Docente: G. VINCENZI
Obiettivi :
Questo corso e’ dedicato all’approfondimento dello studio dei gruppi
risolubili e dei gruppi nilpotenti. Particolare attenzione e’ riservata al
principio di induzione transfinita e ad alcune sue applicazioni.
Contenuti :
Numeri ordinali e numeri cardinali. Il principio di induzione transfinita.
Gruppi Nilpotenti: Struttura dei gruppi Nilpotenti finiti. Serie centrale
superiore, serie centrale inferiore e serie derivata di un gruppo.
Risolubilita’ e nilpotenza per gruppi di matrici. Gruppi Supersolubili,
Gruppi Policiclici , Gruppi di Cernikov.
ANALISI FUNZIONALE
Docente: L. SGAMBATI
Programma del corso
Alcune nozioni preliminari: Nozioni elementari. Sistemi parzialmente
ordinati (P.O.S.). Teorema del punto unito. Teorema di massimalità di
Hausdorff. Lemma di Zorn. P.O.S. ben ordinati. Teorema del buon ordine
di Zermelo. Lemma di Baire.
Teoremi fondamentali di analisi lineare: Forma analitica del teorema dei HahnBanach. Prolungamento di forme lineari. Forme geometriche del teorema di HahnBanach. Separazioni di insiemi convessi. Il principio della uniforme limitatezza con
relative conseguenze. Teorema della applicazione aperta e teorema del grafico
chiuso.
Topologie deboli e spazi convessi: Richiami sulla topologia meno fine
che rende continue le applicazioni di una famiglia. Definizione e proprietà
elementari della topologia debole (E, E’). Topologia debole, insiemi
convessi. Topologia debole*
(E', E). Spazi riflessivi: Teorema di
Kakutani. Spazi separabili.
Spazi LP: Alcuni risultati fondamentali. Definizione e proprietà
elementari degli spazi LP. Riflessività, separabilità, duale di LP con
dimostrazioni relative al caso p
Convoluzione e
regolarizzazione. Supporti e convoluzioni. Mollificatori. Criterio di
compattezza forte in LP. Teorema di Ascoli. Teorema di Riesz-FréchetKolmogorov.
Spazi di Sovolev in dimensione uno: W1,p(I): Motivazione. Definizione
di spazio di Sobolev W1,p(I). Funzioni test. Esempi di funzioni
appartenenti a W1,p(I). Proprietà degli spazi di Sobolev: Riflessività e
separabilità, relazione tra gli elementi W1,p(I) e gli elementi di C (I).
Testi consigliati
DUNFORD, SCHWARTZ - Linea Operators, vol. 1 : Capitolo 1. (Par. 1 e
2 e teor. 9 del Par. 6).
HAIM BREZIS - Analisi funzionale, - Linguori , Napoli: Capitoli 1, 2, 3,
4, 8.
CALCOLO NUMERICO E PROGRAMMAZIONE I
Docente: M.R. CRISCI
Programma del corso
Primo modulo
Nozioni di analisi degli errori. Rappresentazione
dei numeri in un calcolatore. Operazioni di
macchina.
Errori
e
loro
propagazione.
Procedimenti stabili e instabili.
Sistemi di equazioni lineari. Metodi diretti: Il metodo di Gauss e
fattorizzazione LU. Metodi iterativi: Metodi di Jacobi, di Gauss-Seidel.
Convergenza. Malcondizionamento.
Approssimazione. Interpolazione polinomiale. Errore del polinomio
interpolante. Stabilità. Convergenza. Interpolazione con funzioni spline.
Approssimazione nel senso dei minimi quadrati.
Programmazione. Schema dell'architettura di un elaboratore. Concetto di
algoritmo e requisiti. Programmazione strutturata.
Linguaggio di programmazione MATLAB.
Sviluppo di codici relativi ai principali algoritmi trattati.
Secondo modulo
Integrazione numerica. Quadratura interpolatoria. Grado di precisione.
Formule di Newton-Cotes. Espressione dell'errore. Formule composite e
loro errore.
Polinomi ortogonali. Formule di quadratura Gaussiane. Stima dell'errore.
Integratori automatici basati su schemi adattativi.
Autovalori di matrici. Metodi iterativi: metodo delle potenze e delle
potenze inverse. Metodi basati su trasformazioni di similitudine. Le
trasformazioni di Givens ed il metodo di Jacobi.
Equazioni non lineari. Metodi iterativi. Teoremi di convergenza.
Accelerazione della convergenza. Sistemi di equazioni non lineari.
Equazioni algebriche.
Sviluppo di codici relativi ai principali algoritmi trattati.
Software matematico: sviluppo, organizzazione e valutazione. Utilizzo
della libreria di software matematico Nag.
Testi consigliati
V. COMINCIOLI - Analisi numerica - Ed. Mc Graw Hill
Metodi di valutazione
Prova orale preceduta da una discussione sugli elaborati sviluppati
durante il corso o, in assenza di questi, da una prova al calcolatore.
CALCOLO NUMERICO E PROGRAMMAZIONE II
Docente : E. RUSSO
Programma del corso
Risoluzione numerica di equazioni differenziali ordinarie.
Metodi di approssimazione di tipo analitico. Metodi lineari multistep.
Metodi predictor-corrector. Metodi non lineari ad un passo. Metodi
Runge-Kutta. Metodi multistep a passo variabile. Ordine . Stime degli
errori. Consistenza. Convergenza. Zero-stabilità. Teoria della debole
stabilità. Stabilità non lineare. Problemi stiff. Metodi BDF.
Risoluzione numerica di equazioni a derivate parziali.
Fondamenti di teoria. Sistemi di equazioni a derivate parziali lineari del II
ordine. Equazioni paraboliche. Metodi alle differenze finite. Schemi
espliciti ed impliciti. Stima degli errori. Stabilità. Convergenza. Teorema
di Lax. Metodo delle linee. Equazioni di tipo ellittico. Metodi alle
differenza finite. Teorema di unicità della soluzione dello schema. Stima
dell'errore. Convergenza. Metodi risolutivi di tipo iterativo per il sistema
lineare dello schema. Metodo di Jacobi. Metodo di Liebman.
Convergenza.
Calcolo parallelo
Architetture parallele. Indici di valutazione di un algoritmo parallelo.
Parallelismo SIMD e MIMD. Il sistema MPI. Metodi paralleli WR per la
risoluzione di sistemi di equazioni differenziali ordinarie.
Testi consigliati:
J. B. LAMBERT - Computational methods in ordinary differential
equations- J. Wiley Sons
E. ISAACSON, H. KELLER - Analysis of numerical methods - J. Wiley
Sons
V. COMINCIOLI - Analisi Numerica - Ed. Mc Graw Hill
MPI- Manuale
Metodi di valutazione
Prova orale preceduta da una discussione sugli elaborati sviluppati
durante il corso o, in assenza di questi, da una prova al calcolatore.
ISTITUZIONI DI ALGEBRA SUPERIORE
Docenti: P. LONGOBARDI - M. MAJ
Programma del corso
Primo modulo
Elementi di teoria dei gruppi: Derivato di un gruppo. Gruppi risolubili.
Gruppi semplici risolubili. Non risolubilità del gruppo simmetrico Sn , per
n 5. Azione di un gruppo su di un insieme.
Polinomi: Polinomi primitivi, loro proprietà. Lemma di Gauss. Criterio di
Eisenstein. Polinomio derivato. Radici di un polinomio, radici semplici,
radici multiple.
Teoria di Galois: Teoremi di prolungamento. Polinomi separabili,
estensioni separabili. Campi perfetti. Gruppo di Galois di un'estensione.
Teorema di Artin. Estensioni normali. Estensioni normali e separabili.
Estensioni di Galois. Estensioni abeliane, estensioni cicliche, estensioni
ciclotomiche. Teorema fondamentale della teoria di Galois. Gruppo di
Galois di un polinomio. Torre radicale di un' estensione. Equazioni
risolubili per radicali. Caratterizzazione, in campi di caratteristica 0, delle
equazioni risolubili per radicali. Polinomio generico di grado n, gruppo di
Galois del polinomio generico. Teorema di Abel-Ruffini. Campi finiti,
loro proprietà. Lemma di Steinitz e teorema dell'elemento primitivo.
Traccia e norma. Teorema 90 di Hilbert.
Secondo modulo
Numeri cardinali e ordinali: Insiemi equipotenti. Numero cardinale (o
cardinalità) di un insieme. Cardinali finiti e cardinali infiniti. Somma di
numeri cardinali. Teorema di Cantor - Bernstein, teorema di Hartogs.
Insiemi simili. Numeri ordinali.
Categorie: Definizione di categoria. Sottocategorie e sottocategorie piene.
Isomorfismi, monomorfismi, epimorfismi, oggetti equivalenti. Oggetti
iniziali e finali. Funtori covarianti. Funtori controvarianti. Funtori esatti.
Trasformazioni naturali e isomorfismi naturali.
Moduli: Prime definizioni ed esempi. Sottomoduli.
Moduli ciclici, moduli finitamente generati.
Modulo quoziente. Omomorfismi tra moduli.
Sequenze Push-out e pull-back. Moduli semplici.
Moduli indecomponibili. Moduli fedeli. Moduli di
torsione e senza torsione. Prodotto diretto esterno
di una famiglia di moduli. Somma diretta esterna
di una famiglia di moduli. Moduli liberi. Moduli
proiettivi. Moduli iniettivi. Criterio di Baer. Moduli
divisibili.
Moduli su di un anello principale. I funtori Hom. Prodotto tensoriale.
Testi consigliati
T.S. BLYTH - Module Theory - Clarendon Press , Oxford, 1990.
M. CURZIO, P. LONGOBARDI, M. MAJ - Lezioni di algebra Liguori, 1994.
N. JACOBSON - Basic Algebra I, II - Freeman, San Francisco, 1980.
T.W. HUNGERFORT - Algebra - Springer-Verlag, Berlin 1973.
S. LANG - Algebra - Addison-Wesley, Reading, Mass., 1965.
I. STEWART - Galois Theory - Chapman and Hall, London, 1973.
Metodi di valutazione
Prova orale alla fine di ciascun modulo.
ISTITUZIONI DI ANALISI SUPERIORE
Docente: A. VITOLO
Obiettivi:
Il corso si propone di fornire allo studente un’ampia ed approfondita
conoscenza della teoria delle funzioni di variabile complessa, nonché
un’introduzione all’uso di tecniche degli spazi funzionali e metodi di
calcolo che costituiscono parte indispensabile del bagaglio culturale del
matematico e sono d’altra parte largamente utilizzati nelle applicazioni a
problemi concreti. L’obiettivo è di dotare gli studenti - mediante un
inquadramento rigoroso della teoria e la considerazione di vari ambiti di
applicazione - di un sufficiente grado di astrazione in modo da essere in
grado di riconoscere l’applicabilità dei metodi presentati in varie
situazioni concrete e nello stesso tempo – mediante esercitazioni e pratica
di laboratorio con utilizzazione di opportuno software matematico - di un
altrettanto sufficiente capacità di uso delle tecniche e dei metodi di
calcolo.
Programma del corso
Funzioni di variabile complessa – 6 crediti
Rappresentazioni e algebra dei numeri complessi.
Funzioni olomorfe e condizioni di Cauchy – Riemann. Funzioni
armoniche. Serie di potenze. Funzioni polidrome (logaritmo, potenza, …)
Teorema integrale di Cauchy. Formula integrale di Cauchy e applicazioni
(max modulo, media, Morera, Liouville, teorema fondamentale
dell’algebra, …).
Sviluppi in serie di Taylor e di Laurent. Zeri delle funzioni olomorfe.
Classificazione e studio delle singolarità delle funzioni olomorfe.
Teoria dei residui. Indicatore logaritmico. Applicazione al calcolo di
integrali definiti.
Funzioni speciali. Funzione ζ di Riemann.
Spazi funzionali – 3 crediti
Teoria generale della misura e dell’integrazione. Confronto fra vari tipi di
convergenza.
p
Spazi L . Definizione e proprietà. Teorema di Fisher – Riesz.
Approssimazioni con funzioni regolari. Traslazione e compattezza.
n
n 2
2
Spazi di Hilbert. Definizione e proprietà. Modelli: R , C , l , L . Teorema
delle proiezioni.
Funzionali lineari e continui. Teorema di rappresentazione di Riesz.
Sistemi ortonormali. Disuguaglianza di Bessel. Condizioni di
completezza per un sistema ortonormale. Spazi di Hilbert separabili.
2
2
Isomorfismo fra l e L . Il sistema trigonometrico.
Serie e trasformata di Fourier – 3 crediti
Funzioni periodiche e serie di Fourier. Convergenza puntuale, uniforme
integrazione termine a termine della serie di Fourier. Applicazione al
calcolo di serie numeriche.
1
Definizione e proprietà della trasformata di Fourier in L . Teoremi di
1
2
unicità e inversione in L . Estensione a L . Teorema di Plancherel.
Esercitazioni
Calcolo di integrali definiti mediante i teoremi dei residui e di Jordan.
Calcolo di trasformate di Fourier.
Testi consigliati
D.GRECO - Complementi di Analisi Matematica - Liguori (NA).
G.GIUSTI - Analisi Matematica II - Boringhieri (FI).
H.BREZIS Analisi Funzionale - Liguori (NA).
A.TESEI - Istituzioni di Analisi Superiore - Boringhieri (FI).
W.RUDIN - Analisi reale e complessa - Boringhieri (FI).
ISTITUZIONI DI FISICA MATEMATICA
Docente: E. LASERRA
Programma del corso
I modulo
Meccanica Analitica
Equazioni di Lagrange e integrali primi: Relazione ed equazione
simbolica della meccanica. Equazioni di Lagrange. Teorema dell'energia.
Forze potenziali, dissipative e giroscopiche. Equazioni di Lagrange nel
caso di sistemi olonomi soggetti a forze potenziali. Potenziale
generalizzato. Forza di Lorentz. Sistemi lagrangiani generali. Integrali
primi di un sistema lagrangiano. Esempi.
Equazioni canoniche: Teorema di Donkin. Forma canonica delle
equazioni del moto. Integrali primi di un sistema canonico. Esempi.
Parentesi di Lagrange. Parentesi di Poisson.
Principi variazionali: Lemma fondamentale del Calcolo delle variazioni.
Integrale di Hamilton e sua variazione prima. Principio di Hamilton.
Principio di Hamilton-Helmoltz. Principio dell'azione stazionaria.
Analogie tra la dinamica del punto materiale e l'ottica geometrica dei
mezzi isotropi.
Equazione di Hamilton-Jacobi: La funzione principale di Hamilton e
l'equazione di Hamilton-Jacobi. Teorema di Hamilton-Jacobi. Forma
ridotta dell' equazione di Hamilton-Jacobi. Sistemi dinamici di Liouville.
Trasformazioni Canoniche: Definizione. Condizione di S. Lie. Criteri
per individuare trasformazioni canoniche. Esempi. Forma esplicita delle
condizioni di completa canonicità. Spazio delle fasi e aspetto geometrico
delle condizioni di completa canonicita’. Altra dimostrazione del teorema
di Hamilton-Jacobi.
Relazioni invarianti: Relazioni invarianti per un sistema differenziale
ordinario. Condizioni di stazionarietà di una relazione invariante ed
estensione a un sistema di relazioni invarianti. Relazioni invarianti per un
sistema canonico e teorema di Hamilton-Jacobi
Invarianti integrali e alcune notevoli conseguenze: Invarianti integrali
di un sistema differenziale ordinario. Invarianti integrali di un sistema
canonico. Osservazione di Liouville. Invarianza delle parentesi di
Poisson. Interpretazione statistica dell’osservazione di Liouville.
II modulo
Cinematica di un Sistema Continuo: Configurazioni di riferimento. Punti
di vista lagrangiano ed euleriano. Linee di corrente. Linee di flusso.
Equazione di continuità. L'atto di moto e lo spostamento elementare
nell'intorno di un punto del continuo. Coefficienti di dilatazione lineare e
superficiale. Coefficiente di dilatazione cubica.
L'omografia di deformazione: Omografia di deformazione. Omografia
linearizzata di deformazione. Legame tra l’omografia linearizzata di
deformazione e il rotore dello spostamento. Formula di Volterra.
Condizioni di congruenza di Saint Venant.
Equazioni fondamentali della meccanica di un sistema continuo: Sistema
cardinale della meccanica dei continui. Sforzi specifici in un punto. Primo
Teorema di Cauchy. L'equazione fondamentale. Le condizioni al
contorno.
L’equazione vettoriale indefinita. Relazioni di simmetria. Lavoro
elementare delle forze intime. L'equazione simbolica della meccanica dei
continui. Teorema dell'energia. Primo principio della Termodinamica.
Sistemi a trasformazioni reversibili.
Teoria Linearizzata dell'Elasticità: Legge di Hooke. Potenziale elastico
specifico. Corpi iperelastici isotropi. Il sistema differenziale della statica
dei corpi iperelastici isotropi.
Elementi di Geometria differenziale
Algebra Tensoriale: Spazi Vettoriali. Forme lineari. Spazio Duale.
Forme multilineari. Tensori. Prodotto tensoriale. Spazi tensoriali. Algebra
Tensoriale. Operazioni sui tensori. Contrazione. Leggi di trasformazione
dei tensori. Teorema fondamentale dell'algebra tensoriale (criterio di
tensorialità). Tensori simmetrici. Tensori antisimmetrici. Bivettori.
Tensore metrico. Tensori del tipo Ricci. Forme bilineari e forme.
Geometria differenziale classica: Studio locale di una superficie. Curve
tracciate sulla superficie. Triedro di Darboux-Ribaucour (sola
definizione). Le due forme quadratiche fondamentali. Curvatura
normale. Formula di Eulero. Curvatura media. Curvatura totale. Linee di
curvatura. Formule di derivazione di Gauss e Weingarten. Legame tra i
coefficienti della I e della II forma quadratica. Teoremi di Bonnet e di
Janet-Cartan (senza dimostrazione). Geodetiche - Equazioni differenziali
delle geodetiche - Parallele geodetiche. Trasporto parallelo di un vettore
su una superficie. Teorema di Levi-Civita e Teorema di Gauss.
Calcolo differenziale assoluto su una Varietà Riemanniana: Varietà
topologiche e differenziabili. Esempi di Varietà. Spazio tangente. Fibrato
tangente e Fibrato Cotangente. Metrica riemanniana e semi-riemanniana.
Varietà riemanniane.
Campi tensoriali: Campi tensoriali. Tensore fondamentale. Trasporto
parallelo. Connessione Riemanniana - Simboli di Christoffel. Derivazione
covariante di un vettore di un vettore controvariante. Differenziale
assoluto. Geodetiche.
Varietà a connessione affine: Connessione affine. Varietà a connessione
affine. Geodetiche di una Varietà a connessione affine. Torsione di una
Varietà a connessione affine. Trasporto parallelo di un tensore qualunque.
Differenziazione assoluta. Derivata covariante.
Curvatura Riemanniana: Commutatore di due differenziazioni.
Curvatura e parallelismo assoluto. Variazione delle coordinate di un
vettore trasportato parallelamente lungo un contorno chiuso. Tensore di
curvatura in uno spazio riemanniano. Curvatura e angolo di rotazione di
un vettore trasportato parallelamente lungo un contorno chiuso.
Relatività Generale
Richiami di Relatività Ristretta: I postulati della Relatività Ristretta. Le
trasformazioni di Lorentz. Relatività della contemporaneità. Contrazione
delle lunghezze. Dilatazione dei tempi. Composizione delle velocità. Lo
spazio di Minkowski. Classificazione degli eventi rispetto a un evento
dato. 4-vettori e 4-tensori. Le equazioni di Maxwell. Le leggi della
Meccanica Relativistica. Massa dell'energia.
I fondamenti della teoria relativistica della gravitazione: Critiche alla
Teoria Newtoniana e programma della teoria einsteiniana. Lo SpazioTempo della Relatività Generale. Influenza della struttura dello SpazioTempo sui fenomeni fisici. Influenza della materia e del suo moto sulla
struttura dello Spazio-Tempo. Equazioni di campo di Einstein.
Testi consigliati
R.L.BISHOP, S.I.GOLDBERG - Tensor Analysis on manifolds Dover.
G.CARICATO - Lezioni di meccanica analitica - Studium.
G. CARICATO - Lezioni Introduttive alla Meccanica dei Continu Universita' La Sapienza, Roma, 1995.
C.CATTANEO
- Introduzione alla Teoria Einsteiniana della
Gravitazione - Veschi, Roma.
F.R.GANTMACHER - Lezioni di meccanica analitica - Editori
Riuniti.
G.E.SILOV - Analisi Matematica. Funzioni di piu’ variabili reali MIR.
T.LEVI, CIVITA, U.AMALDI - Lezioni di meccanica razionale - Vol
II parte 1a e parte 2a, Editori Riuniti.
E.PERSICO - Introduzione alla Fisica Matematica - Zanichelli (1962).
E.T.WHITTAKER - A treatise on the analytical dynamics of particles
and rigid bodies - Cambridge.
ISTITUZIONI DI GEOMETRIA SUPERIORE
Docente: A. VINOGRADOV
Programma del corso
Parte introduttiva: Fondamenti di geometria degli spazi affini, teorema
generale delle funzione implicite e le sue applicaziononi geometriche,
calcolo delle funzioni a valori vettoriali, formula generalizzata di Leibniz.
Varieta` differenziabili: Sottovarietà geometriche e sottovarietà
parametriche. Carte e atlanti. Varietà differenziabili astratte.
Teoria metrica delle curve: Curve negli spazi affini multidimensionali e
loro struttura topologica, spazi osculatori associati, rango, n-edro di
Frenet, equazioni di Frenet e curvature superiori, teorema della forma
delle curve, teorema di realizzazione delle curvature assegnate, calcolo
pratico delle curvature superiori, curvature orientate, indice topologico
delle curve piane.
Teoria metrica delle superficie: Superficie negli spazi affini ed euclidei
multidimensionali, geometria intrisica delle superficie, la prima forma
fondamentale, curvature normali e la seconda forma fondamentale,
teoremi di Eulero e di Menier, curature e direzioni principali, curvatura di
Gauss, equazioni di Gauss-Wiengarten, teorema della forma delle
superficie, struttura delle superfici sferiche e di curvatura di Gauss zero,
teorema egreggio di Gauss, curve geodetiche e loro proprietà estremali,
geometrie intrinsiche di curvatura di Gauss costante, indipendenza del
quinto postulato e geometrie non-euclidee.
Cenni di geometria riemanniana.
Testi consigliati
W. FULTON - Algebraic curves - Benjamin Inc.
R. WALKER - Algebraic curves - Springer-Verlag.
LOGICA MATEMATICA
Docente: A: DI NOLA
Programma del corso
Il corso tratta della logica matematica. Scopo principale è la
modellizzazione, l'analisi e la meccanizzazione del ragionamento in
ambito matematico e non. Gli argomenti trattati sono legati ai fondamenti
della matematica ed all'intelligenza artificiale. Parte integrante del corso
sono le esercitazioni di laboratorio in cui si apprendono le nozioni base di
programmazione logica. Il primo modulo è propedeutico al secondo. Sono
prerequisiti necessari i contenuti dei corsi di Algebra, Analisi 1 e 2,
Geometria 1 e 2. Utile ma non necessario l'aver seguito il secondo modulo
di Matematiche Complementari.
Primo modulo
Linguaggi formali, grammatiche, operatori di chiusura, calcolo
proposizionale, algebre di Boole, teorema di completezza funzionale,
riduzione a forma normale, operatore di conseguenza logica. Calcolo dei
predicati, modelli, skolemizzazione.
Secondo Modulo
La programmazione logica, programmi e modelli di Herbrand. Teorema
di Completezza. Teoremi limitativi della logica.
Testi consigliati
Negli appunti dal corso può essere trovato tutto quanto detto a lezione.
Per un maggior approfondimento un classico manuale di logica
matematica è:
MENDELSON - Introduzione alla logica matematica - Boringhieri.
Per una trattazione teorica della programmazione logica,
J. W. LLOYD - Fondamenti di programmazione logica - Franco Muzzio
Ed. (esiste una edizione in inglese aggiornata e migliorata di tale testo)
Per i rapporti tra logica e didattica
T. VARGA - Fondamenti di logica per insegnanti - Boringhieri.
Per quanto riguarda l'apprendimento del Prolog si suggerisce il seguente
testo
V. LOIA - Programmazione logica ed un qualunque manuale di Prolog.
MATEMATICHE COMPLEMENTARI
Docente: G. GERLA
Corso di Laurea
Programma del corso
Il corso si occupa di "filosofia della matematica" e quindi di analizzare la
natura delle nozioni-base della matematica. Nel primo modulo si
analizzano, inquadrandole nel contesto storico di origine, le nozioni di
numero, punto, retta, infinito, insieme, dimostrazione. Nel secondo
modulo si analizza la nozione di calcolabilità e, conseguentemente, si
discute su ciò che un calcolatore può o non può fare. I due moduli sono
indipendenti e quindi può essere scelto anche il solo secondo modulo. Per
entrambi i moduli è necessario seguire le esercitazioni di laboratorio per
l'apprendimento del visual-basic.
Primo modulo
La Scuola pitagorica e sua crisi, gli Elementi di Euclide, idealizzazione
degli enti matematici, il Platonismo, Sesto Empirico. Cartesio e la crisi
dell'approccio sintetico. Le geometrie non euclidee. La teoria degli
insiemi. L'aritmetizzazione della geometria e dell'analisi. Infinito attuale
ed infinito potenziale, confronto tra infiniti. Crisi della teoria degli
insiemi, le antinomie. Il metodo assiomatico, il punto di vista
fondazionale e quello strutturalista. Il programma di Hilbert. Il calcolo
proposizionale. Il calcolo dei predicati. Il fallimento del programma di
Hilbert. I teoremi di Goedel.
Secondo modulo
La nozione di calcolabilità. Macchine a memoria finita, gli automi, cose
che un automa finito non può fare. Macchine a memoria infinita,
linguaggi di programmazione evoluti, funzioni ricorsive, Tesi di Church.
Insiemi decidibili, insieme ricorsivamente enumerabili. Cose che una
macchina a memoria infinita non può fare, il teorema della fermata, il
teorema di Rice. Reti sequenziali, reti combinatorie, reti neuronali,
macchine che apprendono.
Testi consigliati
Il programma di entrambi i moduli è contenuto in appunti che possono
essere richiesti al docente. Per un maggiore approfondimento si
consigliano i seguenti testi.
Per la storia della matematica
MORRIS KLINE - La matematica nella cultura occidentale - Feltrinelli.
L.L. RADICE - L'infinito - Editori Riuniti.
BOTTAZZINI, FREGUGLIA, RIGATELLI - Fonti per la storia della
matematica - Sansoni, 1992
ERIC T. BELL - I grandi Matematici - Sansoni, 1966.
B. D'AMORE, M.MATTEUZZI - Gli interessi matematici - Marsilio.
Per quanto riguarda i fondamenti della geometria si consiglia di leggere
direttamente
D. HILBERT - Fondamenti della geometria - Feltrinelli.
Per le geometrie non euclidee
E. AGAZZI, D. PALLADINO - Le geometrie non euclidee - Mondadori.
Per chi fosse interessato alla filosofia della matematica.
E. CASARI - La filosofia della matematica del '900 - Sansoni.
L. GEYMONAT - Storia del pensiero filosofico e scientifico - Garzanti.
D. R. HOFSTADTER - Goedel, Escher, Bach: un eterna Ghirlanda
Brillante.
E. CASARI - Questioni di filosofia della matematica - Feltrinelli.
RUDY RUCKER - La mente e l'infinito - Muzzio, 1991.
WANG HAO - Dalla matematica alla filosofia - Boringhieri, 1984.
C. CELLUCCI - La filosofia della matematica - Laterza ,1967.
Per la teoria della computabilità
M. MINSKY - Computation, finite and infinite machines - Prentice-Hall
International, INC., London.
A.J. KFOURY, R.N. MOLL, M.A. ARBIB - Programmazione e
commutabilità - ETAS libri, 1986.
Prerequisiti
E' opportuno che si siano seguiti i corsi di Algebra, Analisi Matematica
I, Analisi Matematica II, Geometria I, Geometria II.
STORIA DELLE MATEMATICHE
Docente: F. PALLADINO
Programma del corso
I modulo.
Gli Elementi di Euclide. Profilo storico. Studio dei seguenti
capitoli (libri) con relative proposizioni particolari. Libro I: 1, 2, 4, 5, 9,
16, 17, 27, 28, 29, 43, 47; Libro II: 1,2,3,4,5,6,7,9; Libro V: 1,2,3,4,5,6,7;
Libro VI: 1,3,8,13,14,16,23; Libro VII: 1,2; Libro IX:20, 36.
L’Algebra del Cinquecento e l’Algebra di Bombelli: Prefazione,
Analisi dell’opera, Libro I: Radice quadrata e Radice cubica, rispettivi
algoritmi di approssimazione; Libro II: equazioni di primo grado; Libro
IV: Costruzioni geometriche.
La “Formula di Cardano” per la risoluzione delle equazioni
algebriche di terzo grado, il caso irriducibile.
II modulo.
Costruzione di modelli di numeri reali: Sezioni di Dedekind sulla
base del libro V degli Elementi di Euclide. Allineamenti.
Il Seicento: Caratteri generali. Galilei, Discorsi e Dialoghi.
Cartesio: Il metodo, la Géométrie. “Regole” e “Metodi” per il calcolo
della tangente a una curva.
Leibniz e Newton. Origine e sviluppo del calcolo infinitesimale.
TEORIA DELLE FUNZIONI
Docente: V. CAFAGNA
Programma del corso
Preliminari. Calcolo differenziale e integrale: Varietà differenziabili e
sottovarietà. Ipersuperfici. Fibrati tangenti e cotangenti. Campi di vettori:
teorema di esistenza locale per equazioni differenziali ordinarie (EDO).
Mappe differenziabili: rango. Valori regolari e teorema dell'immagine
inversa. Teorema della funzione inversa. Forme differenziali. Teorema di
Green e formula di Stokes. (Riferimenti: [B], [F1], [Ta])
Generalità: Equazioni differenziali alle derivate parziali (EDP).
Notazione di Schwartz (multi-indici). Operatori lineari e quasilineari.
Polinomio caratteristico e varietà caratteristica di un operatore. Esempi:
EDP del primo ordine, equazione di Cauchy-Riemann, equazione di
Laplace, equazione del calore, equazione delle onde. Operatori ellittici.
Ipersuperfici non caratteristiche. (Riferimenti: [F1], [Jo])
Risolubilità locale di EDP del primo ordine a coefficienti reali:
Teorema di esistenza e unicità per EDP del primo ordine lineari a
coefficienti reali con dati su un'ipersuperficie non caratteristica.
Equazioni quasilineari. (Riferimenti: [F1])
EDP del primo ordine a coefficienti complessi: Campi di vettori e
flussi. Parentesi di Lie di campi di vettori. Derivata di Lie. Distribuzioni
tangenti. Integrabilità di distribuzioni. Foliazioni. Condizione di
involutività (Frobenius). Commutatività di flussi. Teorema di integrabilità
completa di Frobenius. Riduzione di un'EDP del primo ordine a
coefficienti complessi verificante la condizione di Frobenius a una
famiglia di equazioni di Cauchy-Riemann sulla foliazione indotta.
(Riferimenti: [B], [N], [Ta])
Esempi di non risolubilità locale: Teorema di Hörmander: la condizione
di integrabilità di Frobenius è necessaria per la risolubilità locale di EDP
del prim'ordine a coefficienti complessi. Il più semplice esempio di EDP
non localmente risolubile: l'operatore di Garabedian-Grushin. Il primo
esempio di EDP non localmente risolubile: l'operatore di Hans Lewy.
Geometria dell'operatore di Hans Lewy: iperquadriche in C2. L'operatore
di Hans Lewy come operatore di Cauchy-Riemann tangenziale ∂ b
sull'iperquadrica. Funzioni CR. (Riferimenti: [B], [F1], [Ja], [K], [N])
Risolubilità locale di EDP lineari a coefficienti costanti: Richiami di
analisi di Fourier: convoluzioni, trasformazioni e antitrasformazioni di
Fourier. Approssimanti dell'identità. Lo spazio delle funzioni test C∞o(Rn).
Funzionali lineari su C∞o(Rn): lo spazio delle distribuzioni D’(Rn). Esempi
di distribuzioni: funzioni di L1loc(Rn), la funzione δ di Dirac. Calcolo
differenziale sulle distribuzioni: la funzione H di Heaviside. C∞o(Rn) è
denso in D’(Rn). La classe di Schwartz S’(Rn) delle funzioni di C∞o(Rn) a
decrescenza rapida e lo spazio S’(Rn) delle distribuzioni temperate.
Trasformazioni di Fourier di distribuzioni temperate. Soluzioni
fondamentali di EDP lineari. Esempi: EDP del primo ordine, equazione di
Cauchy-Riemann, equazione di Laplace: il potenzialeNewtoniano,
equazione del calore: il nucleo Gaussiano. Ipoellitticità e singolarità della
soluzione fondamentale: teorema di Schwartz. Teorema di MalgrangeEhrenpreis: ogni EDP lineare a coefficienti costanti è localmente
risolubile. (Riferimenti: [F2], [H], [Ta], [Tr])
Testi consigliati
[B] BOGGES A. - CR Manifolds and the Tangential Cauchy-Riemann
Complex - CRC Press, Boca Raton, Fl., 1991.
[F1] FOLLAND G.B.- Introduction to Partial Differential Equations Princeton University Press, Princeton, N.J., 1976.
[F2] FOLLAND G.B. - Fourier Analysis and its Applications Wadsworth and Brooks/Cole, 1992.
[H] HÖRMANDER L. - The Analysis of Linear Partial Differential
Operators I - Springer, New York, N.Y., 2nd Ed., 1990
[Ja] JACOBOWITZ H. - An Introduction to CR Structure - Amer. Math.
Soc., Providence, R.I., 1990.
[Jo] JOHN F. - Partial Differential Equations - Springer, New York, N.Y.,
1971.
[K] KRANTZ S.G. - Partial Differential Equations and Complex Analysis
- CRC Press, Boca Raton, Fl., 1992.
[N] NIRENBERG L. - Lectures on Linear Partial Differential Equations Amer. Math. Soc., Providence, R.I., 1973
[Ta] TAYLOR M. - Partial Differential Equations, Basic Theory Springer, New York, N.Y., 1996.
[Tr] TREVES F. - Basic Linear Partial Differential Equation - Academic
Press, New York, N.Y., 1975.
TEORIA DELL’INFORMAZIONE
Docente: V. GIORNO
Programma del corso
Primo modulo
Introduzione: Introduzione alla Teoria dell'informazione e cenni storici.
Obiettivi della Teoria dell'Informazione e aree di interesse. Un semplice
sistema di comunicazione: sorgente, codificatore, canale, decodificatore,
destinazione.
Fondamenti di Calcolo delle Probabilità: Definizione di probabilità.
Approccio assiomatico. Teoremi delle probabilità composte. Teorema di
Bayes. Funzioni misurabili e variabili aleatorie. Leggi di probabilità
Funzioni di variabili aleatorie. Indipendenza di eventi e di variabili
aleatorie. Successioni di eventi e di variabili aleatorie. Concetti di
convergenza. Legge dei grandi numeri. Teorema centrale di convergenza.
Misure di informazione: Autoinformazione, autoinformazione congiunta
e autoinformazione condizionata. Mutua informazione. Entropia di una
variabile aleatoria. Entropia congiunta e condizionata. Mutua
informazione media. Relazioni tra l'entropia e la mutua informazione
media. Divergenza informazionale. Entropia di vettori aleatori. Entropia
congiunta e condizionata di vettori aleatori. Mutua informazione media
per vettori aleatori.
Sorgenti discrete senza memoria: Sorgenti di informazione finite senza
memoria. Codifica di messaggi. Codifica da blocco a blocco. Condizione
di univoca decifrabilità. Sequenze tipiche e sequenze atipiche. Proprietà
di equipartizione asintotica. Teorema di codifica sorgente da blocco a
blocco di Shannon.
Canali di comunicazione discreti: Canali finiti stazionari senza
memoria. Definizione della capacità del canale.
Teorema di codifica canale di Shannon: parte inversa e parte diretta per
sorgenti senza memoria (cenni).
Secondo modulo
Sorgenti discrete senza memoria: Codifica da blocco a lunghezza
variabile. Codici non singolari. Codici univocamente decodificabili.
Teorema di Sardinas e Patterson. Codici a condizione prefissa. Teorema
di McMillan e teorema di Kraft. Teorema di codifica da blocco a
lunghezza variabile. Algoritmo di Huffman per la ricerca di un codice a
condizione prefissa ottimo.
Sorgenti con memoria: Sorgenti di informazione discrete con memoria.
Sorgenti stazionarie. Teorema di codifica da blocco a lunghezza variabile
per sorgenti stazionarie. Sorgenti ergodiche. Teorema di codifica da
blocco a blocco per sorgenti stazionarie ergodiche. Catene di Markov.
Distribuzione limite e distribuzione invariante. Classificazione degli stati
di una catena di Markov. Catene di Markov irriducibili e catene di
Markov ergodiche. Entropia di una catena di Markov. Sorgenti di
Markov. Sorgenti di Markov unifilari e valutazione dell'entropia per
lettera. Reorema di codifica per sorgenti di Markov.
Calcolo della capacità di un canale: Procedura analitica per il calcolo
della capacità. Positività ed unicità del vettore di probabilità di output che
permette di massimizzare la mutua informazione media. Calcolo della
capacità per canali finiti stazionari senza memoria di tipo particolare:
senza rumore, senza perdite, deterministico, inutile per la trasmissione,
strettamente simmetrico, simmetrico e per canali in parallelo.
Codiflca canale: Codifica in presenza di rumore sul canale. Criterio di
decodifica dell'osservatore ideale. Criterio di decodifica con probabilità di
errore uniformemente limitata. Tasso del codice canale e tasso di
informazione. Disuguaglianza di Fano. Teorema di codifica canale di
Shannon: parte inversa. Teorema di codifica canale di Shannon: parte
diretta.
Codici correttori d'errore: Definizione di codice lineare. Matrice
generatrice e matrice a controllo di parità. Codifica per codici lineari.
Decodifica tramite sindrome per codici lineari. Decodifica tramite
sindrome su canali strettamente simmetrici. Geometria di Hamming e
prestazioni di un codice. Regola di decodifica geometrica. Codici di
Hamming binari.
Testi consigliati
COVER M. C. AND THOMAS J. A. - Elements of Information Theory John Wiley & Sons, Inc.
JAN C. A. van der LUBBLE - Information Theory - Cambridge
University Press
LONGO G. - Teoria dell'Informazione - Boringhieri.
FABRIS F. – Teoria dell’Informazione, codoci, cifrari – Boringhieri.
GALLAGER R. - Information Theory and Reliable Communication - J.
Wiley.
MCELIECE R. - The Theory of Information and Coding Addison-Wesley.
ASH R. - Information Theory - J. Wiley.
DALL’AGLIO G. - Calcolo delle Probabilità – Zanichelli
Metodi di valutazione
Prova orale alla fine di ogni modulo.