Esercitazione II - Vettori e cinematica in una dimensione
Vettori
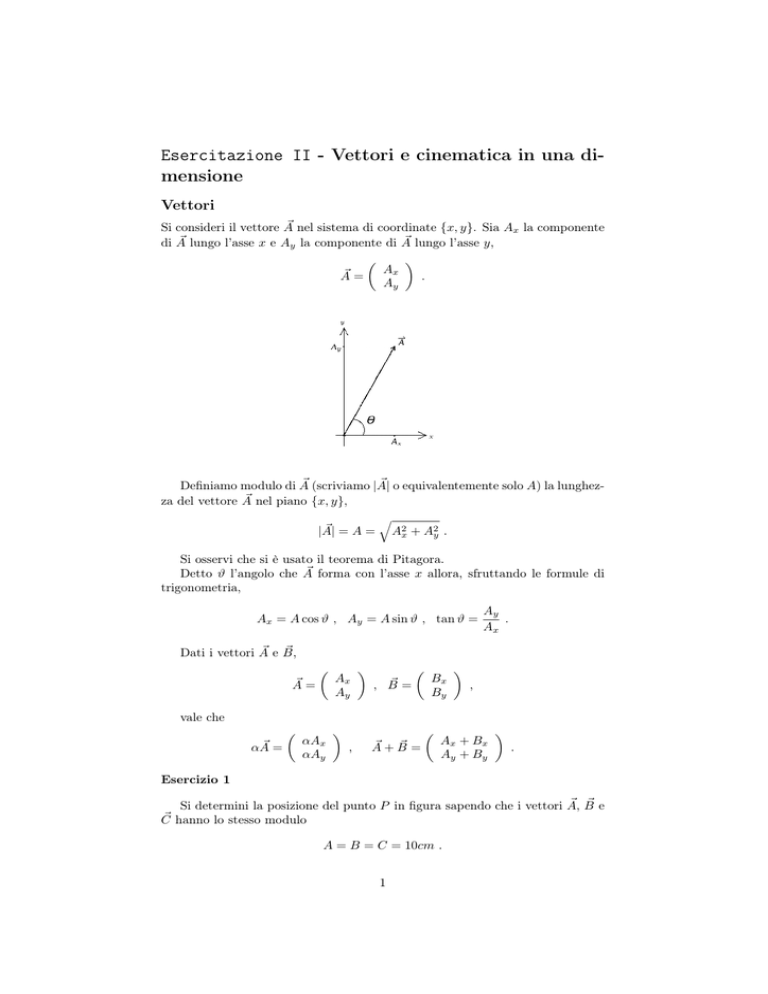
~ nel sistema di coordinate {x, y}. Sia Ax la componente
Si consideri il vettore A
~
~ lungo l’asse y,
di A lungo l’asse x e Ay la componente di A
µ
¶
Ax
~
A=
.
Ay
~ (scriviamo |A|
~ o equivalentemente solo A) la lunghezDefiniamo modulo di A
~ nel piano {x, y},
za del vettore A
q
~ = A = A2x + A2y .
|A|
Si osservi che si è usato il teorema di Pitagora.
~ forma con l’asse x allora, sfruttando le formule di
Detto ϑ l’angolo che A
trigonometria,
Ax = A cos ϑ , Ay = A sin ϑ , tan ϑ =
Ay
.
Ax
~ e B,
~
Dati i vettori A
µ
~=
A
Ax
Ay
¶
µ
~ =
, B
Bx
By
¶
,
vale che
µ
~=
αA
αAx
αAy
¶
µ
,
~+B
~ =
A
Ax + Bx
Ay + By
¶
.
Esercizio 1
~ B
~ e
Si determini la posizione del punto P in figura sapendo che i vettori A,
~
C hanno lo stesso modulo
A = B = C = 10cm .
1
Soluzione
~+B
~ + C.
~ A tal fine iniziamo con lo scrivere i
Dobbiamo calcolare P~ = A
~ B
~ eC
~ in componenti
vettori A,
~
A
~
B
~
C
³
´
√
= (10cm · cos 60◦ , 10cm · sin 60◦ ) = 5cm, 5 3cm ,
= (10cm, 0) ,
= (10cm · cos(−60◦ ), 10cm · sin(−60◦ ))
³
´
√
= (10cm · sin 30◦ , −10cm · cos 30◦ ) = 5cm, −5 3cm .
Da cui
P~ = (20cm, 0) .
Esercizio 2
~ eC
~ hanno lo stesso modulo, B = C = 5cm, calcolare
Sapendo che i vettori B
~
~
~
~ = 0.
il modulo di A affinché A + B + C
Soluzione
Sfruttando i dati in figura si ha
2
~
A
~
B
= (A · cos 45◦ , A · sin 45◦ ) ,
~
C
= (0, −5cm) ,
= (−5cm, 0) ,
da cui
~+B
~ +C
~ = (A · cos 45◦ − 5cm, A · sin 45◦ − 5cm) .
A
~+B
~ +C
~ = 0 se
Poiché cos 45◦ = sin 45◦ si ha A
A · cos 45◦ − 5cm = 0 ⇒ A =
√
5
cm = 5 2cm .
◦
cos 45
Cinematica in una dimensione
Formule
Si ricordi che per un moto uniformemente accelerato si ha
a(t) = a0 ,
v(t) = v0 + a0 t ,
x(t)
1
= x0 + v0 t + a0 t2 ,
2
dove a0 , v0 e x0 sono delle costanti che rappresentano rispettivamente l’accelerazione iniziale, la velocità iniziale e la posizione iniziale.
Le formule per un moto a velocità costante si ottengono dalle precedenti
ponendo a0 = 0, accelerazione nulla. Si ha perciò
a(t)
v(t)
x(t)
= 0,
= v0 ,
= x0 + v0 t .
Esercizio 3
Un pilota parte da fermo e accelera uniformemente con una accelerazione
a0 = 10m/s2 per una distanza d = 0, 4km. Determinare il tempo impiegato e
la velocità finale dell’auto.
Soluzione
Scegliamo come istante iniziale l’istante in cui l’auto parte. Scegliamo un
sistema di riferimento in cui l’origine è il punto in cui l’auto parte e il verso
positivo è il verso del moto dell’auto. Perciò x0 = 0. Inoltre v0 = 0 per ipotesi.
Sfruttando le formule del moto uniformemente accelerato si ha
d =
vf
=
1 2
a0 t ,
2
a0 t ,
3
dove abbiamo indicato con vf la velocità finale raggiunta dall’auto e con t il
tempo impiegato dall’auto per coprire la distanza d.
Dalla prima equazione si ha
r
2d
= 8, 94s .
t=
a0
Dalla seconda si ha
vf =
p
2da0 = 89, 4m/s = 322Km/h .
Esercizio 4
Una locomotiva che viaggia alla velocità iniziale v0 = 26m/s rallenta uniformemente fino a fermarsi in 18s. Quale distanza d ha percorso la locomotiva
da quando ha frenato?
Soluzione
Scegliamo come istante iniziale l’istante in cui la locomotiva inizia a frenare.
Scegliamo un sistema di riferimento in cui l’origine è il punto in cui la locomotiva inizia a frenare e il verso positivo è il verso del moto della locomotiva.
L’accelerazione costante a cui la locomotiva è sottoposta è
a0 =
∆v
vf − v0
v0
=
=−
,
∆t
tf − t0
tf
dove tf = 18s è il tempo impiegato dalla locomotiva per fermarsi.
Sfruttando le formule del moto uniformemente accelerato si ha
1
1
d = v0 tf − v0 tf = v0 tf = 234m .
2
2
Esercizio 5
Sull’autostrada A4 due automobili stanno viggiando in direzione Milano. Ad
un certo istante t0 = 0s l’automobile A passa il casello e procede con velocità
costante vA = 25m/s. Nello stesso istante l’automobile B parte da ferma, con
accelerazione aB = 1m/s2 , da un autogrill posto dopo il casello ad una distanza
pari a xB = 300m. Dopo quanto tempo e a che distanza dal casello l’automobile A raggiungerà l’automobile B? Cosa succederebbe se l’accelerazione
dell’automobile B fosse a0B = 5m/s2 ?
Soluzione
Per risolvere un esercizio di questo tipo, dopo aver imposto un comune
sistema di riferimento, è innanzitutto necessario studiare il moto delle due
automobili. L’automobile A si muove con moto uniforme
x1 = xA + vA t1 = vA t1 ,
dove si è posto il sistema di riferimento con origine sul casello per cui la
posizione dell’automobile A nell’istante iniziale sarà xA = 0m. L’automobile B
si muove invece con moto uniformemente accelerato
4
1
1
x2 = xB + vB t2 + aB t22 = xB + aB t22 ,
2
2
dove si è sfruttato il fatto che l’automobile parte da ferma per cui vB = 0m/s.
L’automobile A raggiungerà l’automobile B quando allo stesso istante avrà
la stessa posizione dell’automobile B, cioè quando
x1 = x2 = x e
t1 = t2 = t ,
da cui si ottiene il sistema di due equazioni in due incognite che risulta
risolvbile
½
x = vA t
.
x = xB + 12 aB t2
Sostituendo il valore di x nella seconda equazione col valore che gli viene
dato nella prima, si ottiene quindi
1
vA t = xB + aB t2 ,
2
da cui è possibile ricavare l’equazione di secondo grado
t2 −
2vA
2xB
t+
=0.
aB
aB
Come spiegato nella lezione precedente la risoluzione di questa equazione
dipende dal valore che assume il discriminante,
µ
¶2
2vA
2xB
∆= −
−4
= 100s2 ,
aB
aB
che risulta positivo e porta quindi ad avere due soluzioni
t−
=
t+
=
√
− (−2vA /aB ) − ∆
= 20s ,
2
√
− (−2vA /aB ) + ∆
= 30s .
2
Ovviamente il tempo richiesto è il primo in quanto rappresenta la prima
volta che le due automobili si incrociano.
Per calcolare la distanza dal casello a cui questo avviene è, infine, sufficiente
sostituire il tempo ricavato in una delle due equazioni originarie per ottenere la
posizione dell’automobile in questione in quel dato istante
x = vA t− = 500m .
Un buon metodo di controllo della correttezza dell’esercizio svolto risulta
l’essere il calcolare la posizione anche della seconda automobile
1
x = xB + aB t2− = 500m .
2
5
Qualora la posizione delle due automobili risulti essere effettivamente uguale
(così come imposto inizialmente) l’esercizio sarà probabilmente corretto.
Si osservi che quando l’automobile A sorpassa l’automobile B, A procede
con velocità costante vA = 25m/s mentre B ha accelerato fino a raggiungere la
velocità
vB (t− ) = aB t− = 20m/s .
Dopo essere stata sorpassata l’automobile B continua ad accelerare, aumentando quindi la propria velocità, mentre l’automobile A procede a velocità
costante. Ad un certo istante la velocità della seconda automobile risulterà
quindi maggiore di quella della prima, così che nell’istante t = t+ l’automobile
B potrà superare nuovamente l’automobile A.
L’esercizio richiede infine di studiare cosa succederebbe se l’accelerazione
dell’automobile B fosse pari a a0B = 5m/s2 : in questo caso il discriminante
dell’equazione di secondo grado risulterebbe pari a
µ
¶2
2vA
2xB
∆= − 0
− 4 0 = −380s2 ,
aB
aB
quindi l’equazione non avrebbe soluzioni reali. Questa situazione rappresenta
il caso in cui l’automobile B riuscirà a raggiungere una velocità maggiore di
quella dell’automobile A, prima che questa l’abbia superata, così che le due
automobili non si potranno incrociare.
6












