Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
CINEMATICA
La cinematica è una branca della meccanica classica che si occupa
dello studio del moto dei corpi senza preoccuparsi delle cause
che lo determinano.
determinano
Tecnicamente si parla di cinematica del punto materiale in quanto i
corpi in movimento vengono considerati come punti (es. il
baricentro di un corpo reale) senza massa nè dimensione.
Grandezze fisiche coinvolte:
- Tempo Æ s
- Spazio percorso (lunghezza) Æ m
- Velocità Æ m s-1
- Accelerazione Æ m s-2
1
FISICA – CdL Tecnologie Agroalimentari
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Concetto di moto
Il moto di un punto materiale avviene lungo una linea (detta
traiettoria), che può essere una retta o una curva qualsiasi nel
piano o nello spazio.
Occorre definire un riferimento, costituito da un oggetto
immobile, che fissa un punto di partenza e un sistema di assi
coordinati.
Durante il moto, in un certo intervallo di
tempo Δt=t2-t1, il punto si muove tra P1
e P2 lungo la traiettoria.
I vettori r1 e r2 rappresentano,
rispettivamente,
i
tti
t la
l posizione
i i
di P1
e P2 nel sistema di riferimento
scelto.
r1 = r1 x ⋅ i + r1 y ⋅ j + r1 z ⋅ k
r2 = r2 x ⋅ i + r2 y ⋅ j + r2 z ⋅ k
FISICA – CdL Tecnologie Agroalimentari
2
1
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Moto unidimensionale (1)
Per semplicità si inizierà la trattazione partendo dal caso più semplice: il
moto lungo una sola direzione ossia il moto lungo una linea retta
(traiettoria rettilinea).
rettilinea)
x
xf
Q
x
x
x0
tf
t
P
t0
I vettori spazio (posizione), velocità ed accelerazione sono
sempre paralleli alla retta che definisce la traiettoria, ciò che
varia nel tempo è il loro modulo ed eventualmente il verso.
3
FISICA – CdL Tecnologie Agroalimentari
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Moto unidimensionale (2)
ESEMPIO (Auto che percorre un tratto rettilineo di Corso Allamano)
t
t0
P
t
x0=0
NB. Quanto segue, se non
diversamente
specificato,
è
relativo al moto unidimensionale
FISICA – CdL Tecnologie Agroalimentari
4
2
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
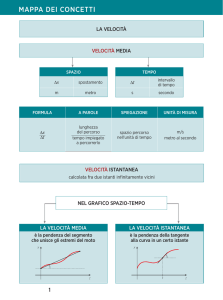
Velocità Media (1)
Il moto di un punto materiale è completamente definito conoscendo,
istante per istante, la sua posizione.
Si consideri un punto che si muove lungo un tratto rettilineo (es.
(es ll’asse
asse x)
tra due punti P e Q.
x0 Æ posizione di P al tempo t0
xf Æ posizione di Q al tempo tf
P
Q
x0
xf
Δx
5
FISICA – CdL Tecnologie Agroalimentari
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Velocità Media (2)
In tempi diversi tra t0 e tf la posizione può variare (arbitrariamente) come
nel diagramma spazio-tempo illustrato.
Nell intervallo di tempo Δt
Nell’intervallo
Δt=(t
(tf -tt0) il punto si è spostato, complessivamente,
di una quantità Δx = ( x f − x0 ) (Vettore spostamento)
x
xf
Velocità media di una
particella è il rapporto tra il
vettore spostamento ed
l’intervallo di tempo Δt
Q
Δx
x0
P
t0
vm =
Δt
FISICA – CdL Tecnologie Agroalimentari
tf
t
Δ x x f − x0
=
t f − t0
Δt
6
3
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Velocità Media (3)
La velocità media NON DIPENDE dal particolare percorso tra P e Q.
La velocità media non fornisce alcun dettaglio relativamente al moto tra P e
Q.
x
xf
SIGNIFICATO GEOMETRICO
Q
La velocità media è il
coefficiente angolare della
retta passante per i punti P
(iniziale) e Q (finale) nel
grafico spazio-tempo.
Δx
x0
P
t0
tf
Δt
t
7
FISICA – CdL Tecnologie Agroalimentari
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
x
PERCHÉ ?
Q
xf
Δx
x0
P
Δt
t0
tf t
Ricordando come si ricava il coefficiente angolare m di una retta passante
per due punti si ottiene:
m=
x f − x0
FISICA – CdL Tecnologie Agroalimentari
t f − t0
=
Δx
= vm
Δt
8
4
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Velocità Istantanea (1)
Velocità del punto in un qualsiasi istante di tempo, ossia in un qualsiasi
punto del grafico spazio-tempo.
La velocità media non descrive cosa avviene effettivamente tra i due
punti, infatti suddividendo l’intervallo Δt in intervalli più piccoli…
…la
velocità
media
calcolata
in
ciascuno
degli intervalli è diversa
da quella calcolata tra P
e Q e diversa in ciascun
intervallo.
x
Come calcolare la velocità x0
in un generico istante di
tempo t ?
Δt
Q
P
t0
t1
t3
t2
tf
t
9
FISICA – CdL Tecnologie Agroalimentari
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Velocità Istantanea (2)
Si consideri l’intervallo di tempo x
tra t0e tf ( indicato con Δt ) e la
rispettiva velocità media.
Q
Se si riduce progressivamente
Δt (Δt Æ 0)…
x0
P
t0
t1
t2
t3
tf
t
Δt
FISICA – CdL Tecnologie Agroalimentari
10
5
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Velocità Istantanea (3)
Si consideri l’intervallo di tempo x
tra t0 e tf ( indicato con Δt ) e la
rispettiva velocità media.
Q
S sii riduce
Se
id
progressivamente
i
t
Δt (Δt Æ 0)…
… la retta che originariamente
definiva la velocità media
diventa tangente alla curva nel
punto ti.
x
x0
P
t0
La velocità istantanea è la
pendenza retta tangente al
grafico
spazio-tempo
nel
generico istante t.
t1
x0
t2
P
t3
tf
t
t
t0
11
FISICA – CdL Tecnologie Agroalimentari
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Velocità Istantanea (4)
DEFINIZIONE:
La velocità istantanea è il limite per Δt Æ 0 della velocità media
calcolato in un genetico istante di tempo t
v = lim
Δ t→ 0
Δ x
d x (t )
=
Δ t
dt
OSSIA è la derivata nel tempo dello spazio percorso
x (t )
calcolata in un determinato istante t.
FISICA – CdL Tecnologie Agroalimentari
12
6
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Velocità Istantanea (5)
La velocità istantanea può essere positiva, negativa o nulla.
x
v
v=0
v<0
v>0
tf
t
t0
t0
t
tf
13
FISICA – CdL Tecnologie Agroalimentari
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Velocità Istantanea (6)
Se la velocità istantanea è la derivata nel tempo dello spazio percorso
calcolata in un determinato istante t allora, nota la velocità lo spazio
percorso si può
ò calcolare come:
t
x − x0 =
v
∫ v ( t ) dt
t0
Che corrisponde all’area
t
tf
t0
FISICA – CdL Tecnologie Agroalimentari
t
compresa tra la curva e
l’asse delle x.
14
7
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Moto rettilineo uniforme (1)
Il vettore velocità istantanea è costante in modulo direzione e
verso per qualunque t, quindi la pendenza della retta tangente alla
traiettoria è sempre costante.
Lo spazio percorso cresce (decresce) linearmente nel tempo.
x
v ≡ vm
Q
xf
v ≡ vm =
Δx
Δx
⇒ Δx = v ⋅ Δt
Δt
x0
P
Δt
t0
tf
t
15
FISICA – CdL Tecnologie Agroalimentari
Università degli Studi di Torino – D.E.I.A.F.A.
Davide Ricauda A.
Moto rettilineo uniforme (2)
Trattandosi di un moto rettilineo si può confondere il vettore Δx con il suo
modulo Δx.
Δx = v ⋅ Δt ⇒ Δx = v ⋅ Δt
x − x0 = v ⋅ (t − t0 )
Legge oraria del moto
rettilineo uniforme .
Se t0 = 0 :
x
x − x0 = v ⋅ t
v
v
x
x0
t
FISICA – CdL Tecnologie Agroalimentari
t
t
t
16
8