5 - Gaia Edizioni

I numeri dell’estate
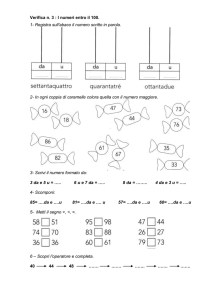
Completa scrivendo i numeri mancanti in ordine crescente.
1 281
....................
4 699
....................
6 898
....................
1 283
1 282 ....................
4 701
4 700 ....................
3 690 ....................
3 691
3 689 ....................
....................
8 999
8 998 ....................
....................
3 000 ....................
3 001
2 999 ....................
2 998 ....................
8 008
....................
3 692
8 010
8 009 ....................
9 001 ....................
9 002
9 000 ....................
Individua e scrivi i numeri.
Sono maggiori di 6 997
e minori di 7 000.
Sono compresi
tra 2 356 e 2 359.
2 357
....................
6 900
6 899 ....................
6 998
....................
6 999
....................
2 358
....................
Seguono 7137 e
precedono 7141.
In ciascun numero
compare la cifra 3.
Sono minori di 6 001
e maggiori di 5 998.
5 999
....................
6 000
....................
7 138
....................
7 139
....................
Scrivi cifre adatte in modo da rendere vera ogni relazione.
1 5.....
06
1516 > .....
2 > .....
8 261
8 26.....
6 6 = 4.....
6 6.....
6
4 6.....
4 6.....
1
4 450 < 4.....
2 315
.....
3 75
< 2.....
9 6 < .....
5 5.....
02
5 1.....
4 5.....
9
6 520 > 6.....
8 79 = 3 87.....
9
3.....
1 6 > 2.....
9 1.....
1
2 9.....
Il nostro esempio
4
NEL MONDO DEI NUMERI I numeri fino a 9999
Cifre al gusto di...
Leggi il numero sulla cassetta, poi evidenzia la cifra che corrisponde
al valore scritto su ogni frutto seguendo lʼesempio.
3 555
5u
5h
4 434
4u
6 766
6da
3h
3 393
30h
8da
8 888
800u
4k
7 877
7u
6k
70u
Osserva gli esempi e componi i numeri.
3k 4h 8da 1u
3 481
......................
2 000 + 400 + 20 + 3
2 423
.........................
5k 2h 7da 3u
5 273
......................
3 000 + 600 + 80 + 1
3 681
.........................
5 970
..................................
2k 9h 6da
2 960
.............................
5 000 + 900 + 70
2k 4da 6u
2 046
.............................
2 000 + 30 + 8
2 038
........................................
9 000 + 900 + 9
9 909
.....................................
50h 3da
5 030
.................................
Scrivi il numero minore
e il numero maggiore
che puoi comporre
usando tutte le cifre
di ogni gruppo.
7
4 9
5
4 579
.....................
2
6
8
1
9 754
.....................
NEL MONDO DEI NUMERI I numeri fino a 9999
1 268
.....................
8 621
.....................
5
Che tana!
Segui il comando delle frecce e raggiungi lʼuscita!
9 200
+ 50
– 50
+ 200
– 1000
8 200
....................
7 200
....................
4 100
....................
6 200
....................
3 900
....................
5 200
....................
5 250
....................
4 200
....................
4 250
....................
3 200
....................
3 250
....................
3 700
....................
4 150
....................
4 200
....................
3 750
....................
3 550
....................
3 300
....................
3 350
....................
Individua e scrivi il comando delle frecce, poi esegui i calcoli.
+..................
2 000
3 236
– 300
..................
–..................
1 100
6
7 900
9 400
5 236
....................
7 600
....................
8 300
....................
7 236
....................
9 236
....................
7 300
....................
7 200
....................
7 000
....................
6 100
....................
LE OPERAZIONI Il calcolo orale entro 9999
Non solo rette
Osserva e ripassa di verde le rette, di giallo le semirette,
di blu i segmenti. Usa il righello.
Osserva ogni gruppo di rette e classificalo
secondo la legenda.
I
Pe
rette incidenti
Pe rette perpendicolari
I
Pa rette parallele
Pa
Pa
I
Leggi e continua tu a disegnare la serie di segmenti consecutivi
usando il righello. Tracciane almeno quattro.
Il nostro esempio
Due segmenti sono
consecutivi se hanno
un estremo in comune.
LA GEOMETRIA Rette, semirette, segmenti
7
In colonna e in riga
Esegui le operazioni in colonna, poi scegline due
per ogni pagliaio ed esegui la relativa prova. Usa le
Pagine a quadretti in fondo al libro.
7 958 – 1872 =
917 + 2 821 =
9 530 – 5 895 =
6 468 + 3 347 =
4 500 – 2127 =
517 + 9 020 + 148 =
6 000 – 3 296 =
75 + 4 220 + 315 =
7 857 : 23 =
2 213 x 4 =
9 436 : 42 =
1198 x 8 =
5 475 : 13 =
305 x 32 =
7142 : 56 =
139 x 69 =
Esegui le operazioni con il calcolo in riga.
1 98 9
1861 + 128 = ..................
7 391
7 042 + 349 = ..................
6 393
2131 x 3 = ..................
1 688
844 x 2 = ..................
8
4 132
5 493 – 1361 = ..................
700
1245 – 545 = ..................
4 123
8 246 : 2 = ..................
2 410
7 230 : 3 = ..................
LE OPERAZIONI Il calcolo in colonna e in riga
La domanda sottintesa
Leggi ogni problema, scrivi la domanda sottintesa, risolvi e rispondi.
Il pasticciere sistema 50 gelatine su ciascuno
dei 3 vassoi della vetrina. Se 90 gelatine
sono alla fragola e le altre sono ai mirtilli,
quante sono le gelatine ai mirtilli?
La risoluzione
50
3
x
La domanda sottintesa è:
150
Quante sono in tutto le gelatine?
................................................................................................................
90
–
La risposta
60
Le gelatine ai mirtilli sono 60.
................................................................................................................
In un negozio di souvenir sono state vendute
160 cartoline a colori e 40 in bianco e nero.
Se le cartoline esposte erano 400,
quante sono quelle ancora in vendita?
La risoluzione
160
40
+
La domanda sottintesa è:
Quante cartoline sono state vendute?
................................................................................................................
200
400
–
La risposta
Le cartoline ancora in vendita sono 200.
................................................................................................................
200
Osserva il diagramma e risolvi, poi scrivi il testo di un
problema adatto che preveda la domanda sottintesa.
20
280
Francesca ha sfornato 280 biscotti al
..........................................................................................................
+
cioccolato e 20 alla cannella.
..........................................................................................................
300
100
–
Se ne regala 100 a Paola, quanti
..........................................................................................................
biscotti le restano?
..........................................................................................................
Il nostro esempio
200
..........................................................................................................
I PROBLEMI A una domanda e due operazioni
9
Strategie!
Calcola e completa le tabelle seguendo le indicazioni.
Per aggiungere 9, 99, 999
prima somma 10, 100, 1 000,
poi sottrai 1 .
+
9
374
383
99
999
473 1 373
1425 1 434 1 524 2 424
Per togliere 9, 99, 999
prima sottrai 10, 100, 1 000,
poi somma 1 .
–
9
99
999
1340 1 331 1 241 341
6 693 6 684 6 594 5 694
Calcola e collega ogni operazione al rispettivo risultato.
533 + 9 =
1534
542
533 + 99 =
632
533 + 999 =
1532
544
1444
1543 – 9 =
1543 – 99 =
1543 – 999 =
Risolvi i problemi con
il calcolo in riga.
In un grande allevamento si
contano 645 mucche bianche
e 99 pezzate. Quante mucche
ci sono nell’allevamento?
645 + 99 = 744
................................................................
10
Questa mattina nella malga
di Camillo c’erano 350 forme
di formaggio. Se ne sono
rimaste 99, quante forme di
formaggio sono state vendute?
350 – 99 = 251
................................................................
LE OPERAZIONI Strategie di calcolo
` di + e –
Le proprieta
Completa ogni regola, poi applicala seguendo lʼesempio.
ADDIZIONE
Proprietà
addendi
commutativa Cambiando l’ordine degli ................................................
cambia
la somma non ..................................
.
200 + ............
125 = ............
325
58 + ..........
41 = ..........
99 • 125 + 200 = ............
• 41 + 58 = ..........
73 + ..........
32 = 105
301 + ............
50 = ............
351
• 32 + 73 = ..........
..........
• 50 + 301 = ............
Proprietà
associativa
addendi
Se si sostituisce a due o più ..................................
la loro
non cambia
.
somma, il risultato ..................................................
52
2 + ..........
18 ) + ..........
32 = ..........
20 + ..........
32 = ..........
• 2 + 18 + 32 = (..........
35 + (..........
11 + ..........
9 ) = ..........
35 + ..........
20 = ..........
55
• 35 + 11 + 9 = ..........
49 + (..........
17 + ..........
23 ) = ..........
49 + ..........
40 = ..........
89
• 49 + 17 + 23 = ..........
95 + ..........
5 ) + ..........
39 = ............
100 + ..........
39 = 139
• 95 + 5 + 39 = (..........
............
SOT TR AZIONE
Proprietà
invariantiva
numero
Aggiungendo o togliendo lo stesso ........................................
al
minuendo
, il risultato non cambia.
sottraendo e al .....................................
50
97 – 47 = ..........
10
36 – 26 = ..........
150
230 – 80 = ..........
+3
6
–6 –
.......
+.......
20 + 20
100
..........
+3
50 = ..........
50
– ..........
30
..........
20 = ..........
10
– ..........
250
.......... =150
..........
.......... – 100
Segui le indicazioni per calcolare più rapidamente.
prima scambia
poi associa
11 + 56 + 89 =
9 + 300 + 41 =
89 + ..........
56 =
11 + ..........
300
...............
9 + 41 =
+ ...............
100
56 = ...............
156
.......... + ..........
300
...............
50 = ...............
350
+ ..........
LE OPERAZIONI Le proprietà di addizione e di sottrazione
11
Sport in vacanza
Osserva il cartellone che riporta le iscrizioni alle attività sportive di un
villaggio turistico, poi rappresenta i dati nellʼistogramma e completa.
Ogni ✗ indica
un iscritto!
tennis
✗✗✗✗
✗✗✗
acquagym
✗✗✗✗✗
✗✗✗
surf
✗✗✗✗✗✗
✗✗✗✗
canottaggio
✗✗✗✗✗
✗✗✗✗
calcetto
✗✗✗✗✗
✗✗✗
tennis
surf
vale 1 iscrizione
canottaggio
acquagym
calcetto
il surf
L’attività sportiva che rappresenta la moda è .................................
maggior
numero
perché è quella che ha ricevuto il ............................................
di iscrizioni dai turisti del villaggio.
Osserva il grafico e completa.
9
• Il numero degli iscritti al corso di canottaggio è ....................
.
42 .
• Il numero totale degli iscritti alle attività sportive è ....................
• L’attività sportiva che ha ricevuto il minor numero di iscrizioni
il tennis
è ..............................................................
.
• I due corsi che hanno ricevuto lo stesso numero di iscritti
l’acquagym e il calcetto
sono .....................................................................................................................................
.
12
LA STATISTICA L’istogramma e la moda
` tempo di giochi!
E
Osserva ogni angolo che Marta ha realizzato con i bastoncini
dello Shangai e classificalo seguendo la legenda.
A acuto
R retto
R
O ottuso
P piatto
O
G giro
A
P
G
Leggi e colora il cartellino con la risposta esatta.
• Quanto misura un angolo retto?
120°
• Quanto misura un angolo giro? 360°
• Quanto misura un angolo piatto?
90°
90°
120°
360°
• Quanto può misurare un angolo acuto?
95°
• Quanto può misurare un angolo ottuso?
100°
360°
90°
180°
30°
90°
180°
9°
Colora gli angoli interni delle figure: di rosso se sono
acuti, di giallo se sono retti e di verde se sono ottusi.
LA GEOMETRIA Gli angoli
13
Frazioni in montagna
Leggi e colora per
rappresentare la
frazione.
2
5
3
4
1
8
11
12
2
3
4
6
• Quale, tra queste frazioni,
indica unʼunità frazionaria?
Riscrivila qui!
1
........
8
........
Osserva le frazioni rappresentate e completa la tabella.
rappresentazione
frazione numeratore denominatore
5
......
6
......
6
......
8
......
9
........
10
........
7
........
12
........
14
si legge
5
..........
6
..........
cinque sesti
........................................................
6
..........
8
..........
sei ottavi
........................................................
9
..........
10
..........
nove decimi
........................................................
7
..........
12
..........
sette dodicesimi
........................................................
LE FRAZIONI Rappresentazione, lettura, scrittura
Ventagli!
FR AZIONI COMPLEMENTARI
Osserva e scrivi la
frazione complementare
a quella data, poi somma:
otterrai lʼintero!
4
9
5 + ........
= ........ = 1
9 ........
9
9
........
2
5
3 + ........
= ........ = 1
5 ........
5
5
........
2
3
1 + ........
= ........ = 1
3 ........
3
3
........
4
6
2 + ........
= ........ = 1
6 ........
6
6
........
Collega ogni
frazione alla sua
complementare.
Usa le linee.
3
7
9
13
2
7
2
9
11
20
3
9
5
7
9
20
6
9
4
13
4
7
7
9
FR AZIONI EQUIVALENTI
Scrivi le frazioni rappresentate e collega con le linee quelle che
indicano la stessa quantità, cioè quelle equivalenti.
2
........
3
........
6
........
1
........
2
........
8
........
12
........
9
........
4
........
3
........
LE FRAZIONI Complementari ed equivalenti
15
In piscina
Osserva lʼillustrazione, poi leggi e completa.
• Nella prima corsia si trova Paolo, che ha già percorso
4
........
5
........
• Nella seconda corsia si trova Mara, che ha già percorso
• Nella terza corsia si trova Fabio, che ha già percorso
2
........
5
........
3
........
5
........
• Nella quarta corsia si trova Elena, che ha già percorso
della vasca.
della vasca.
della vasca.
1
........
5
........
della vasca.
Paolo
Chi tra i ragazzi ha compiuto il percorso più lungo? ................................................
• Riscrivi in ordine decrescente le frazioni
corrispondenti ai vari percorsi.
4
........
5
........
>
3
........
5
........
>
2
........
5
........
>
1
........
5
........
Q U IZ A C QU A TI CO
5
del tragitto della
8
3
gara, Vela Gialla ne ha percorso i .
8
Vela Blu ha percorso i
Vela Gialla
Quale barca ha percorso il tratto più corto? ...............................................
Perché?
16
3
........
8
........
<
5
........
8
........
LE FRAZIONI Il confronto
Poligoni e non poligoni
Completa il disegno di ogni figura seguendo le indicazioni dei pianeti,
poi leggi la definizione e sottolinea i termini corretti.
Il nostro esempio
Non poligoni!
Poligoni!
Un poligono è una figura piana delimitata
da una linea mista/spezzata chiusa/aperta.
Ripassa di verde i lati del poligono, indica con un
di giallo gli angoli, poi completa.
triangolo
3
n° lati ............
3
n° vertici ............
3
n° angoli ............
pentagono
5
n° lati ............
5
n° vertici ............
5
n° angoli ............
LA GEOMETRIA I poligoni
i vertici e colora
quadrilatero
4
n° lati ............
4
n° vertici ............
4
n° angoli ............
esagono
6
n° lati ............
6
n° vertici ............
6
n° angoli ............
17
Ss... si calcola!
Leggi e applica il calcolo della frazione di un numero seguendo
lʼesempio, poi colora la relativa quantità.
3
di 14
7
14 : ......
7 ) x ......
3 = ......
2 x ......
3 = ..........
6
(..........
Prima dividi
il numero intero per
il denominatore...
Poi moltiplica per
il numeratore!
18
5
di 24
8
24 : ..........
8 ) x ..........
5 = ..........
3 x ..........
5 = .............
15
(.............
4
di 18
6
18 : ..........
6 ) x ..........
4 = ..........
3 x ..........
4 = .............
12
(.............
2
di 20
5
20 : ..........
5 ) x ..........
2 = ..........
4 x ..........
2 = .............
8
(.............
LE FRAZIONI Il calcolo della frazione di un numero
Le frazioni nei problemi
Risolvi i problemi ricorrendo al calcolo della frazione di un numero,
poi rispondi colorando il riquadro esatto.
5
degli
9
81 gelati in vendita. Qual è il numero dei gelati venduti?
Oggi al bar della spiaggia sono stati acquistati
5
9
di 81
(81 : 9) x 5 = 9 x 5 = 45
Il numero dei gelati venduti è 36 45 120 .
4
di un libro di 77 pagine.
7
Qual è il numero delle pagine lette?
Il bagnino ha già letto i
4
7
di 77
(77 : 7) x 4 = 11 x 4 = 44
Il bagnino ha già letto 11 33 44 pagine del libro.
Risolvi ricorrendo al calcolo della frazione complementare.
3
delle 25 conchiglie che aveva raccolto
5
sulla spiaggia. Quante conchiglie gli sono rimaste?
Matteo ha perso
Individua la frazione
complementare.
Calcola il valore
della frazione
complementare.
2
3 ........
5
+
=
=1
5
5 ........
5
2
........
5
........
5 ) x ......
2 = ......
5 x ......
2 = ..........
10
di 25 = (25 : ......
A Matteo sono rimaste 8 10 12 conchiglie.
LE FRAZIONI E I PROBLEMI
19
Numeri... in bottiglia!
Leggi ogni numero in lettere e scrivilo in cifre nella bottiglia.
trecentosettantaseimilanovecentoventuno
376 921
novecentonovantamilatrecentoquarantanove
990 349
settantaseimilaventicinque
76 025
centocinquantatremilaseicentodiciotto
153 618
86 809
ottantaseimilaottocentonove
22 142
ventiduemilacentoquarantadue
Leggi e riscrivi i numeri in
ordine crescente.
576 439
99 943
997 458
5 864
570 839
5 864
...................................
99 943
...................................
570 839
...................................
576 439
...................................
997 458
...................................
Leggi e riscrivi i numeri in
ordine decrescente.
441 461
483 741
76 375
39 357
997 500
997 500
...................................
483 741
...................................
441 461
...................................
76 375
...................................
39 357
...................................
Confronta i numeri e completa con i segni > oppure <.
20
15 343 < 51627
900 000 > 690 990
81234 < 81654
62 000 > 60 007
4 201 < 42 017
27 873 < 270 378
NEL MONDO DEI NUMERI I numeri fino a 999 999
Completa la tabella scrivendo al posto giusto
i termini migliaia e unità, poi unisci ogni cifra
evidenziata al relativo valore come nellʼesempio.
classe delle
migliaia
...............................
hk
367193
dak
uk
524 458
340 263
classe delle
unità
...............................
semplici
h
da
67175
77 452
u
54 321
4 925
425 540
Leggi e circonda il numero corrispondente.
3hk
30 000
5uk
300 000
5 000
34uk
34 000
340
2dak
500 000
20
12dak
12 000
20 000
60uk
120 000
60 000
6 000
Leggi e componi i numeri.
5hk 1dak 2uk 3h 8da 4u
4hk 6dak 8uk 2da 3u
16dak 2uk 7u
512 384
...............................
468 023
...............................
162 007
...............................
2hk 8dak 2da 1u
3hk 12uk 5h 4u
30dak 400u
280 021
...............................
312 504
...............................
300 400
...............................
NEL MONDO DEI NUMERI I numeri fino a 999 999
21
Calcoli in viaggio
Calcola seguendo le indicazioni delle frecce.
+ 2h
- 7 da
+ 3 uk
30 070
33 000
........................
33 070
........................
+ 3 dak
129 201
........................
- 20 uk
- 20 da
139 001
........................
139 201
........................
23 200
........................
33 200
........................
+ 6 uk
- 2 dak
109 201
........................
- 1 dak
+ 1u
123 201
........................
+ 1 hk
123 200
........................
+ 9u
- 10 uk
119 001
........................
109 001
........................
109 010
Calcola e... completa i cartelli.
+ 10 000
5 000
15 000
...............................
40 000
240 000
...............................
7 000
17 000
...............................
290 000
490 000
...............................
42 000
52 000
...............................
320 000
520 000
...............................
190 000
200 000
...............................
495 000
695 000
...............................
– 20 000
22
+ 200 000
– 500 000
70 000
50 000
...............................
900 000
400 000
...............................
30 000
10 000
...............................
801 000
301 000
...............................
28 000
8 000
...............................
540 000
40 000
...............................
25 000
5 000
...............................
506 000
6 000
...............................
LE OPERAZIONI Il calcolo orale entro 999 999
Strane piramidi...
Classifica ogni triangolo in base agli angoli: collegalo alla giusta
descrizione, poi scrivi se è rettangolo, ottusangolo o acutangolo.
B
E
triangolo
ottusangolo
..............................................
D
triangolo
F
H
acutangolo
..............................................
A
C
triangolo
rettangolo
..............................................
G
Ha un angolo retto.
I
Ha tre angoli acuti.
Ha un angolo ottuso.
• Ora classifica i triangoli in base ai lati collegando i cartellini corretti.
Ha due lati uguali.
triangolo ABC
equilatero
Ha tutti i lati uguali.
triangolo DEF
isoscele
Ha tutti i lati disuguali.
triangolo GHI
scaleno
Leggi e completa, poi osserva gli angoli dei
triangoli e scrivi le misure mancanti.
45°
La somma degli angoli interni
di un triangolo corrisponde a un
angolo piatto, cioè è di 180
.............°.
40 °
........
110°
30°
LA GEOMETRIA I triangoli
90 °
........
45°
23
10, 100, 1000
Esegui le moltiplicazioni e le divisioni.
46
460
x 10 = .......................
4 600
x 100 = .......................
5 000
x 100 = .......................
500
x 10 = .......................
50
46 000
x 1000 = .......................
6 000
600
: 10 = .......................
60
: 100 = .......................
50 000
x 1000 = .......................
20 000
6
: 1000 = .......................
20
: 1000 = .......................
2 000
: 10 = .......................
200
: 100 = .......................
Segui le frecce e completa scrivendo
il termine mancante.
450
10
x .............
8 000
000
:1
.............
100
: .............
100
: .............
45 000
4 500
100
x .............
100
x .............
000
x1.............
45
80
8
10
: .............
800
Risolvi i problemi con il calcolo in riga.
Se un vaso contiene 14 piantine,
quante piantine contengono
100 vasi uguali?
14 x 100 = 1 400
................................................................
24
Una macchina distribuisce
36 000 semi in parti uguali
in 1000 buste. Quanti semi
distribuisce in ogni busta?
36 000 : 1 000 = 36
................................................................
LE OPERAZIONI Moltiplicazioni e divisioni per 10, 100, 1000
` di X e :
Le proprieta
Completa ogni regola, poi applicala seguendo lʼesempio.
MOLTIPLICAZIONE
ordine
Cambiando l’..............................
dei fattori
prodotto
non cambia.
il ............................................
Proprietà
commutativa
20 x ..........
4 = ..........
80
• 4 x 20 = ..........
66 x ..........
10 = .............
660
• 10 x 66 = ..........
Proprietà
associativa
70 x 100
7 000
.......... = ................
• 100 x 70 = ..........
25 x ..........
4 = .............
100
• 4 x 25 = ..........
fattori
Se si sostituisce a due o più ..................................
il loro
non cambia
.
prodotto, il risultato ..................................................
250
25 x (..........
5 x ..........
2 ) = ..........
25 x ..........
10 = ...............
• 25 x 5 x 2 = ..........
8 x ..........
5 ) x ..........
6 = ..........
40 x ..........
6 = ...............
240
• 8 x 5 x 6 = (..........
16 x (..........
50 x ..........
2 ) = ..........
16 x 100
600
• 16 x 50 x 2 = ..........
.......... = 1
...............
Proprietà
distributiva
fattore e moltiplicando ogni numero
Scomponendo un ............................
non cambia
.
ottenuto per l’altro fattore, il prodotto ...............................................
28 x 4 =
31 x 5 =
20 + ..........
8 )x4=
(..........
30 + ..........
1 )x5=
(..........
20 x 4) + (..........
8 x 4) =
(..........
30 x 5) + (..........
1 x 5) =
(..........
80
..........
32 = .............
112
+ ..........
150
.............
5 = .............
155
+ ..........
DIVISIONE
Proprietà
invariantiva
Moltiplicando o dividendo i termini della divisione per
quoziente
non cambia.
lo stesso numero il ............................................
240 : 10) : (..........
80 : 10) = ..........
24 : ..........
8 = ..........
3
• 240 : 80 = (..........
70 x 2) : (..........
5 x 2) = .............
140 : ..........
10 = ..........
14
• 70 : 5 = (..........
60 : 2) : (..........
12 : 2) = .............
30 : ..........
6 = ..........
5
• 60 : 12 = (..........
LE OPERAZIONI Le proprietà di moltiplicazione e di divisione
25
Come un mandala
Esegui le operazioni nelle Pagine a quadre tt i in fondo al libro e
riporta i risultati, poi colora ogni spazio seguendo la legenda.
39 061
32 058 + 7 003 = ...........................
460 115
2 356 + 457 759 = ...........................
2 844
79 x 36 = ...........................
10 696
382 x 28 = ...........................
3 752
145 + 79 + 3 528 = ...........................
89 871
950 + 31825 + 57 096 = ...........................
66 402
714 x 93 = ...........................
144 184
2 152 x 67 = ...........................
431 903
499 512 – 67 609 = ...........................
700 059
880 607 – 180 548 = ...........................
221
9 503 : 43 = ..................
51
1785 : 35 = ..................
410 926
778 391 – 367 465 = ...........................
708 149
994 901 – 286 752 = ...........................
1 208
28 992 : 24 = ..................
619
46 425 : 75 = ..................
risultati delle
addizioni
risultati delle
sottrazioni
risultati delle
moltiplicazioni
431 903
619
708 149
51
144 184
89 871
39 061
66 402
3 752
410 926
26
10 696
460 115
2 844
Il mandala è un disegno
realizzato con tante polveri
colorate. Incrociando
cerchi e quadrati, l’autore
cerca di rappresentare la
complessità del Mondo.
risultati delle
divisioni
1208
221
LE OPERAZIONI Il calcolo in colonna
700 059
La scorta di problemi
Risolvi i problemi nelle
Pagine a quadretti in fondo al libro.
A In un grande villaggio turistico è stato organizzato un
torneo di pallavolo. Si iscrivono 241 partecipanti, di
cui 127 sono femmine. Se le squadre sono composte
da 6 giocatori ciascuna e possono essere solo maschili o
femminili, quante squadre maschili si potranno formare?
C
B Durante una partita ai
videogiochi Fausto conquista
prima 10 028 punti, poi altri
997, infine ancora 2 748.
Se Mara, la sua sfidante,
ha conquistato in totale
16 907 punti, qual è la
differenza tra i punteggi
dei due ragazzi?
D
In una fabbrica di giocattoli
vengono prodotte 2 605 biglie
ogni giorno. Se ogni 5 giorni
le biglie vengono distribuite
in 25 scatole per la
spedizione, quante biglie
contiene ogni scatola?
Per il torneo di rugby sono
state formate 8 squadre
composte da 15 ragazzi
ciascuna. All’ultimo
momento 2 squadre
decidono di ritirarsi.
Quanti ragazzi gareggiano?
I PROBLEMI
Per risolvere questo
problema ci sono
due procedimenti possibili:
individuali e applicali.
27
Cabine... decimali!
Colora secondo
lʼindicazione della
frazione, poi scrivi
il numero decimale
corrispondente.
3
10
4
100
0,04
...............
7
100
5
10
0,3
..........
23
100
0,07
...............
8
10
0,5
..........
54
100
0,23
...............
0,8
..........
0,54
...............
Trasforma ogni frazione in numero decimale.
18
10
1,8
...............
341
100
8
1000
3,41
...............
23
1000
0,008
..................
0,023
..................
Collega ogni frazione decimale al numero decimale corrispondente.
Usa le linee.
28
9
1000
9
100
0,09
0,031
9
10
0,009
31
10
0,9
31
100
0,16
31
1000
0,31
16
100
3,1
LE FRAZIONI Le frazioni decimali e i numeri decimali
Sulla linea
Collega ogni numero decimale alla relativa tacca, come nellʼesempio.
0,7
0
2,9
0,6
1
2
1,8
0,3
2,5
3
2,7
1,4
Leggi ogni numero e sottolinea la parte decimale, poi uniscilo alla
scomposizione corrispondente.
0,4
4 centesimi
6,5
6 unità e 5 decimi
0,04
4 decimi
0,65
6 centesimi 5 millesimi
0,004
4 millesimi
0,065
6 decimi 5 centesimi
Componi i numeri con lʼaiuto della tabella, come nellʼesempio.
scomposizione
k
6h 5da 1u e 3c
h
da
u
d
c
6
5
3
5
1
2
6
0
3
3
3
4
8
0
8
0
2
0
0
5
0
8
3da 2u e 3d 4c 9m
5da 6u e 3d
80u e 8c
5k e 25d
8da e 8m
5
0
m
in cifre
651,03
.........................
9
32,349
.........................
56,3
.........................
80,08
.........................
5 002,5
.........................
0
8
80,008
.........................
• Riscrivi i numeri in ordine crescente.
32,349 < ........................
56,3 < ........................
80,008 < ........................
80,08 < ........................
651,03 < ........................
5 002,5
........................
NEL MONDO DEI NUMERI I numeri decimali
29
La caccia al tesoro
PRIMA PROVA
Completa seguendo le indicazioni delle frecce.
+ 5d
+ 2c
– 3m
– 2d
6,1
6,6
.......................
7,12
9,148
4,89
7,1
.......................
7,14
.......................
9,145
.......................
4,69
.......................
7,6
.......................
7,16
.......................
9,142
.......................
4,49
.......................
8,1
.......................
7,18
.......................
9,139
.......................
4,29
.......................
7,2
.......................
9,136
.......................
4,09
.......................
SECONDA PROVA
Completa le addizioni e le sottrazioni scrivendo il termine mancante.
0,5
0,5 + ..........
0,2
0,8 + ..........
1
0,7
0,3 + ..........
0,06
0,94 + ...............
0,03
0,97 + ...............
1
0,01
0,99 + ...............
0,49
0,51 + ...............
0,1
0,9 + ..........
0,7
1,7 – ..................
1
1
0,006
0,994 + ..................
30
0,48
1,48 – ..................
0,009
0,991 + ..................
0,001
0,999 + ..................
0,011
0,989 + ..................
0,031
1,031 – ..................
1,5
2,5 – ..................
LE OPERAZIONI Il calcolo orale con i numeri decimali
TERZA PROVA
Esegui le moltiplicazioni e le divisioni per completare le tabelle.
x 10
15,37
x 100
153,7
x 1000
3,274
327,4
0,306
306
7,38
738
33,4
33 400
127,02 1 270,2
0,03
0,3
12,1
1 210
1,08
1 080
81,4
814
0,009
0,9
5,9
5 900
: 10
: 100
: 1000
38,1
3,81
316,1
3,161
1248
1,248
94,8
9,48
2,4
0,024
543
0,543
4,24
0,424
36
0,36
79
0,079
171
17,1
8
0,08
1
0,001
QUARTA PROVA
Completa i confronti con numeri adatti.
0,81
0,4 < ...................
9,7
9,3 < ...................
25,33
25,12 < ...................
Il nostro esempio
57,01
57,1 > ...................
0,431
0,341 < ...................
12,34
12,4 > ...................
15,11
15,41 > ...................
37,8
39,8 > ...................
0,001
0,002 > ...................
QUINTA PROVA
Segui le frecce, calcola e raggiungi il “trofeo”.
9,67
– 1,1
– 0,06
9,61
: 10
0,961
+ 0,008
96,9
95,8
: 10
x 100
9,58
0,969
+ 0,02
10
x 10
100
+ 0,4
9,6
LE OPERAZIONI Il calcolo orale con i numeri decimali
31
Anguria per tutti
Il signor Rino ha realizzato il grafico delle fette di anguria
che ha venduto durante la scorsa settimana...
vale 10 fette
vendute
lunedì
martedì
mercoledì
giovedì
venerdì
sabato
domenica
0 10 20 30 40 50 60 70 80 90 100
Osserva il grafico e scrivi
il numero delle fette vendute
ogni giorno.
L
Ma Me
G
V
S
D
90 ..........
10 ..........
80 ..........
20 100
70 ..........
50
.......... ..........
..........
• Completa e calcola la media aritmetica delle fette vendute al giorno.
10 + ..........
80 + ..........
20 + 100
70 + ..........
50 ) : 7 = ...............
420 : 7 = ..........
60
90 + ..........
(..........
.......... + ..........
• Individua la mediana: scrivi i dati numerici in ordine crescente e colora
la casella con il numero centrale della serie.
10
20
50
70
80
• Scrivi qual è il giorno in cui si sono registrate più
vendite, cioè il giorno che rappresenta la moda.
32
90
100
Venerdì
................................................
LA STATISTICA Media, mediana, moda
Disegno io!
Leggi e indica con una X se ogni affermazione è vera ( V ) oppure
falsa ( F ), poi disegna i trapezi.
trapezio isoscele
• Ha i due lati obliqui di uguale
misura. V F
• Ha tutti gli angoli diversi tra loro. V
F
trapezio scaleno
• Ha un lato perpendicolare
alle basi. V F
• Ha tutti gli angoli diversi tra loro. V
F
trapezio rettangolo
• Ha un lato perpendicolare
alle basi. V F
• Ha due angoli retti. V
F
Completa le definizioni scrivendo al giusto posto trapezi e
parallelogrammi, poi colora le figure seguendo le indicazioni.
trapezi
I ....................................
hanno
una coppia di lati paralleli.
parallelogrammi hanno
I ......................................................
due coppie di lati paralleli.
Colorali di azzurro!
Colorali di verde!
LA GEOMETRIA I trapezi e i parallelogrammi
33
Euro... Cent!
Conta il denaro che contiene ogni salvadanaio
ed esprimi il valore in euro e in cent.
1,15 = ..............
115 cent
€ .............
72 cent = € .............
0,72
..............
2,45 = ..............
245 cent
€ .............
16
..............
0,16
cent = € .............
1 euro vale 100 cent
1,55 = ..............
155 cent
€ .............
30
..............
0,30
cent = € .............
Collega ogni oggetto al prezzo che ritieni più adatto.
€ 98,45
34
€ 23
€ 6,90
200 cent
LA MISURA Le misure di valore
90 cent