Moto Parabolico

Moto Parabolico
Sino ad ora abbiamo visto due tipi di moto:
moto rettilineo uniforme
moto uniformemente accelerato
lo studio che è stato condotto fino a questo punto ha preso in considerazione un moto alla volta,
senza esaminare la possibilità di verificare quale sia il risultato dell’azione combinata di due moti su
un corpo.
A tal fine consideriamo un esempio come punto di partenza per le nostre considerazioni.
Supponiamo di dare un calcio ad una palla. Quale traiettoria descriverà nel suo moto?
Richiamiamo il significato di traiettoria.
Definizione: si definisce traiettoria di u punto la curva geometrica descritta dal corpo durante il sul
moto.
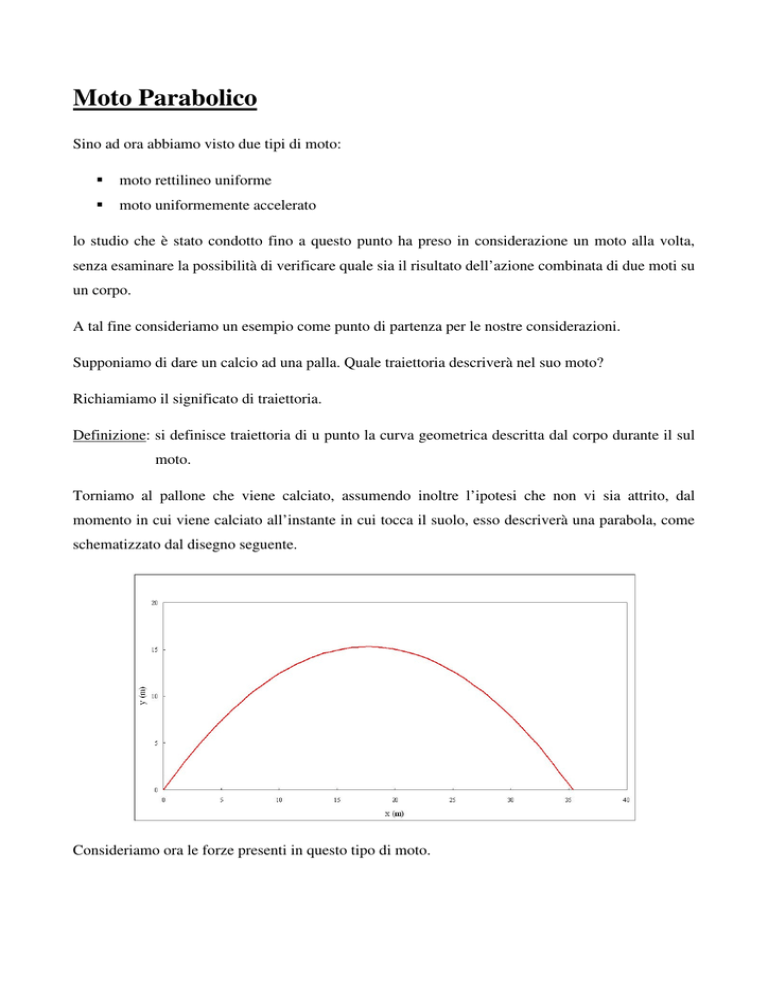
Torniamo al pallone che viene calciato, assumendo inoltre l’ipotesi che non vi sia attrito, dal
momento in cui viene calciato all’instante in cui tocca il suolo, esso descriverà una parabola, come
schematizzato dal disegno seguente.
Consideriamo ora le forze presenti in questo tipo di moto.
Vi è una forza iniziale, un impulso che imprime al velocità iniziale, essa però dura soltanto per
l’istante iniziale, poi la sua azione termina e il pallone prosegue il moto grazie all’azione subita al
momento del lancio.
Analizziamo allora le forze presenti nell’azione descritta. Se non consideriamo la spinta iniziale,
causa del moto, per gli istanti t > 0 (cioè successivi al lancio che corrisponde all’istante t = 0 ,
unico momento in cui agisce al forza iniziale) possiamo scomporre il moto lungo gli assi:
asse x: non agisce alcuna forza, pertanto il moto sarà rettilineo uniforme e il valore della
velocità lungo l’asse orizzontale dipende unicamente dalle condizioni iniziali;
asse y: lungo l’asse verticale agisce la forza di gravità che, con la sua azione verso il basso,
si oppone alla spinta verticale iniziale la quale dipende a sua volta dalle condizioni iniziali
del moto, pertanto, vista la presenza della forza di gravità (e quindi dell’accelerazione di
gravità) il moto lungo l’asse y sarà rettilineo uniformemente accelerato.
Nelle considerazioni precedenti è stato fatto riferimento più volte alle condizioni iniziali, vediamo
di chiarire che significato abbiano.
Con condizioni iniziali ci riferiamo precisamente:
alla velocità iniziale v0 di lancio;
all’angolo che la velocità iniziale v0 forma con la direzione positiva dell’asse delle x.
Infatti se manteniamo costante la velocità di lancio iniziale v0 e facciamo variare l’angolo che il
vettore velocità iniziale v0 forma con la direzione positiva dell’asse delle x, si può osservare che:
Situazione 1
y
v0
α
x
Situazione 2
y
v0
α
x
Situazione 3
y
v0
α
x
Si può osservare che se v0 rimane costante, la distanza tra il punto di lancio e il punto di impatto
varia al variare dell’angolo di lancio α , quindi esso è responsabile della distanza percorsa dal
corpo, in quanto l’unica forza che agisce nella situazione esaminata è la forza di gravità che risulta
costante per tutte le situazioni illustrate. Nelle possibilità viste, infatti l’unica grandezza che varia è
proprio l’angolo α , quindi esso è la causa della variazione di distanza percorsa dal corpo lanciato.
Analogamente, se manteniamo fisso l’angolo di lancio α e facciamo variare la velocità iniziale v0 ,
si ha:
Situazione 1
y
v0
α
x
Situazione 2
y
v0
α
x
Situazione 3
y
v0
α
x
Si può osservare che se α rimane costante, la distanza tra il punto di lancio e il punto di impatto
varia al variare del valore iniziale della velocità di lancio v0 ora, quindi, è tale valore il responsabile
della variazione di distanza percorsa dal corpo, in quanto, come osservato in precedenza, l’unica
forza che agisce nella situazione esaminata è la forza di gravità che risulta costante per tutte le
situazioni illustrate. Nei 3 precedenti casi visti, infatti l’unica grandezza che varia è proprio la
velocità iniziale, quindi essa è la causa della variazione di distanza percorsa dal corpo lanciato.
Allora, poiché la velocità è una grandezza vettoriale, ha senso parlare delle sue componenti, in
particolare della componente orizzontale v0 x e della componente verticale v0 y , che si ottengono
scomponendo il vettore v0 .
y
v0 y
v0
α
x
v0 x
Come è possibile determinare le componenti così rappresentate a partire dalla velocità iniziale v0 e
dall’angolo di lancio α ?
A questo problema viene risposto con l’utilizzo delle funzioni goniometriche, pertanto per ora,
utilizzando la calcolatrice, prenderemo per valide le seguenti formule, senza entrare nel merito della
loro dimostrazione.
v0 x = v0 cos(α )
v0 y = v0 sin (α )
Osservazione
Se avessimo invece v0 x e v0 y è possibile calcolare v0 utilizzando il teorema di Pitagora, infatti:
v0 = v02x + v02y
Analizziamo ora le componenti della velocità
Componente orizzontale
Nel caso di v0 x , nell’ipotesi che non vi si attrito per il moto considerato, una volta impressa la
spinta iniziale, non vi è alcuna forza che interagisca con v0 x pertanto non è presente alcuna azione
che modifichi il valore iniziale della componente orizzontale della velocità
quindi
lungo l’asse x il moto è rettilineo uniforme e dipende esclusivamente dal valore iniziale della
velocità e dall’angolo di lancio, cioè
vx = v0 x .
Componente verticale
Nel caso di v0 y , sempre nell’ipotesi che non vi si attrito per il moto considerato, una volta impressa
la spinta iniziale, vi è la forza di gravità che interagisce con la componente verticale di v0 pertanto
i questo caso è presente un’azione che modifica il valore iniziale della componente verticale della
velocità, inoltre poiché la spinta iniziale è diretta verso l’alto, mentre la forza di gravità è diretta
verso il basso, esse avranno segno opposto
quindi
lungo l’asse y il moto è rettilineo uniformemente accelerato e dipende dal valore iniziale della
velocità, dall’angolo di lancio e dalla forza di gravità, cioè
v y = v0 y − gt .
Dalle formule delle velocità e dalla natura dei moti, possiamo ottenere le formule per lo spazio
percorso, cioè l’equazione oraria del moto per al direzione verticale e per al direzione orizzontale:
s x = v0 x ⋅ t
s y = v0 y ⋅ t −
1 2
gt
2
Osservazione
Poiché il moto complessivo è un moto parabolico, che avviene in un determinato intervallo di
tempo ∆t , anche le componenti del moto dovranno anch’esse svolgersi nello stesso intervallo di
tempo. Ecco quindi che nelle formule s x = v0 x ⋅ t e s y = v0 y ⋅ t −
1 2
gt , il tempo rappresenta sempre
2
lo stesso valore, cioè per determinare al posizione del corpo in un istante si dovrà sostituire lo stesso
valore di t in entrambe le formule.
Analogamente il tempo totale di volo dell’oggetto è lo stesso per entrambe le formule.
Quindi il tempo è la variabile che mi permette di passare da un moto all’altro, egli è l’elemento che
mette in comunicazione le due componenti in cui si scompone il moto parabolico.
Altezza massima di un moto parabolico
Se proiettiamo il moto del punto che si muove di moto parabolico sull’asse delle x abbiamo moto
rettilineo uniforme, mentre se proiettiamo sull’asse delle y abbiamo moto uniformemente
accelerato.
In quest’ultimo caso, però, il moto che si ottiene sull’asse verticale è un moto in cui il corpo sale
sino a che non raggiunge il punto di altezza massima, che coincide con il vertice della parabola,
successivamente il corpo scende e la sua proiezione sull’asse delle y scende anch’essa fino a zero
valore che coincide con l’impatto del corpo al suolo.
Se analizziamo il comportamento della proiezione verticale del moto, osserviamo che esso si
comporta come un oggetto che viene lanciato verso l’alto , sottoposto al’azione della forza di
gravità, cioè è in pratica la caduta di un grave.
Per tale moto allora, ricordando quanti visto in precedenza, è possibile calcolare il tempo necessario
per raggiungere l’altezza massima, poiché per questa situazione è possibile osservare che per un
istante la velocità verticale del corpo è nulla, cioè accade:
0 = v0 y − gt
da cui si ottiene
t=
v0 y
g
Che rappresenta il tempo necessario al corpo per raggiungere l’altezza massima.
Sostituendo tale valore per il tempo nell’equazione s y = v0 y ⋅ t −
1 2
gt , troviamo l’altezza massima
2
raggiunta dal moto del corpo:
hmax
1  v0 y
= v0 y ⋅
− g 
g 2  g
v0 y
2
v02y 1 v02y 1 v02y

 =
− ⋅
=
g 2 g
2 g

Per determinare la posizione del corpo in tale istante si deve sostituire il medesimo valore del tempo
nella formula s x = v0 x ⋅ t .
Osservazione
Dal momento che la parabola è una curva simmetrica, il tempo necessario per andare dal punto di
lancio al punto di altezza massima è lo stesso che serve per andare dal punto di altezza massima al
punto di impatto.
Ricordiamo ora che la distanza percorsa da un corpo in moto è la distanza tra il punto finale e il
punti iniziale, indipendentemente dalla traiettoria, pertanto si deve stare attenti a non confondere tra
loro distanza percorsa e traiettoria del corpo.
Definizione: si definisce gittata di un corpo la distanza tra un il punto di lancio e il punto di impatto.
La gittata allora non è altro che lo spazio percorso dal corpo nel suo moto di traslazione orizzontale.
Quindi se si conosce il tempo necessario al corpo per giungere all’altezza massima t h , si ha che il
tempo totale di volo è il doppio di questo valore ttot = 2t h , tale valore è anche il tempo totale di
traslazione orizzontale del corpo, cioè la gittata L è data dalla formula:
L = v0 x ⋅ ttot
La gittata inoltre si può anche calcolare con la formula
L=
2 ⋅ v0 x ⋅ v0 y
g
Osservazione
Poiché la gittata si può calcolare in due modi, uguagliando tra loro le due espressioni è possibile
ottenere il tempo totale di volo oppure v0 y , infatti
v0 x ⋅ ttot =
ttot =
2 ⋅ v0 y
g
2 ⋅ v0 x ⋅ v0 y
g
che si può esprimere anche v0 y =
g ⋅ ttot
2
Osservazione
Se in un problema si conosce l’altezza massima il tempo di caduta si calcola considerando la
proiezione verticale del punto, che coincide con la caduta di un grave, quindi
t=
2hmax
g
Tale valore del tempo, moltiplicato per due restituisce il tempo totale di volo.
Osservazione: caso particolare di un moto parabolico lanciato orizzontalmente
Consideriamo ora il caso di lancio orizzontale per un corpo.
y
v0
h
x
In questo caso si ha
v0 x = v0
v0 y = 0
Quindi si può sintetizzare che tale moto corrisponde ad un moto parabolico, nel caso generale, che
cade dal punto di altezza massima.
Allora il tempo di volo coincide con il tempo di caduta di un grave che cade da un’altezza h .
Come visto in precedenza:
[tempo volo]= [tempo traslazione]= [tempo caduta]
Tempo di caduta t =
2h
.
g
Spazio percorso durante la caduta h =
1 2
gt .
2
Spostamento lungo l’asse orizzontale x = v0 x ⋅ t (è la gittata).