Scheda - 14 - Corsi di Laurea a Distanza

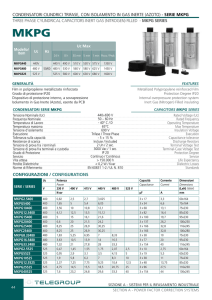
Schede di Elettrotecnica
Corso di Elettrotecnica 1 - Cod. 9200 N
Diploma Universitario Teledidattico in
Ingegneria Informatica ed Automatica
Polo Tecnologico di Alessandria
A cura di Luca FERRARIS
Scheda N° 14
Sistemi trifase:
• Sistemi simmetrici ed equilibrati
• Connessioni a stella e triangolo
• Potenze
• Rifasamento
Scheda N° 14 - Sistemi trifase
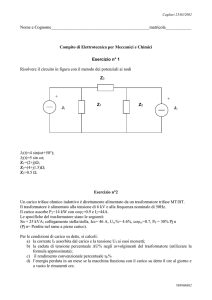
ESERCIZIO 14.1
E’ data la rete trifase di figura alimentata con una tensione alternata di 260 V concatenati a 50 Hz.
Ad essa sono collegati due carichi in parallelo:
• il primo carico è rappresentabile con un collegamento a stella di una resistenza (R1 = 16 Ω) e di
una induttanza (XL1 = 12 Ω) in serie;
• il secondo è approssimabile con un collegamento a triangolo di una resistenza (R2 = 50 Ω) e di
una induttanza (XL2 = 50 Ω) in serie.
In parallelo a questi due carichi viene collegata una batteria di condensatori di rifasamento.
Si vuole conoscere:
• la corrente che circola nella rete prima del rifasamento
• lo sfasamento del carico totale senza condensatori
• la capacita necessaria per rifasare a cosϕ = 0,9.
1
V
2
I”1
I’1
3
X1
X2
R1
R2
E1
C
Per calcolare i dati richiesti si faccia riferimento al monofase equivalente nel quale bisogna inserire le
impedenze stellate; bisogna trasformare il collegamento a A
triangolo in un collegamento
r a stella: essendo i tre rami ad
I’1
r
I”1
Z
uguale impedenza: ZY = ∆ .
3
X1
X2/3
E
Il circuito risulta pertanto quello della figura accanto;
C
imponendo
che
la
fase
della
tensione
sia
nulla
si
ottiene:
R
1
R2/3
r
B
r V 260 + j0 260
E=
=
=
3
3
3
260
r
r
E
3 = 2, 6 ⋅ 4 − j ⋅ 3 A
I1′ = r =
(
)
Z1 16 + j⋅12
3
260
r
r
E
3
I2′′ = r =
= 2,6 3 ⋅ (1 − j ⋅1)A
Z 2 50 1 + j ⋅1
(
)
3
r r r
2,6
⋅ (4 − j⋅ 3) + 2,6 3 ⋅ (1 − j ⋅1) = (10,5 − j ⋅ 9)A = 13,84 ⋅ e − j⋅40,6°
I1 = I1′ + I2′′ =
3
1
Scheda N° 14 - Sistemi trifase
Ora si può passare al dimensionamento dei condensatori.
Siano Q1 e P1 la potenza reattiva e attiva assorbita dai carichi e Prif e Qrif la potenza attiva e reattiva
complessiva dopo il rifasamento:
PT = E ⋅ I1 ⋅ cos(ϕ ) = 1577,3 W

Q T = E ⋅ I1 ⋅ sen(ϕ) = 1352 VAr
Prif = PT

~
Q rif = Prif ⋅ tg(ϕ ) = 1577,3 ⋅ tg ar cos(0,9) = 763,94 VAr
[
]
Q COND = Q rif − Q T = 763,94 − 1352 = −588,06 VAr
CY =
Q COND
E2 ⋅ ω
=
588
2
 260 

 ⋅ 2 ⋅ π ⋅ 50
 3
= 83,22 µF
Se i condensatori vengono connessi a triangolo sarà necessaria una capacità pari a:
1
C ∆ = C Y = 27,7 µF
3
2
Scheda N° 14 - Sistemi trifase
ESERCIZIO 14.2
Con riferimento al circuito in figura si richiede di calcolare la tensione V letta dal Voltmetro e la
capacita dei condensatori necessari per rifasare a cosϕ = 0,9 sapendo che:
• I = 4 A;
• W1 = 1430 W;
• W2 = 195 W.
Calcolare le letture dei Wattmetri qualora la linea 2 venga interrotta per un guasto.
+
+
W1
+
1
V
+
W2
Carico
equilibrato
+
2
+
3
A
I3
La disposizione dei Wattmetri è di tipo Aron per cui valgono le seguenti relazioni:
⇒ Sia per carichi equilibrati che squilibrati.
P = W1 + W2

Q = 3 ⋅ (W1 − W2 ) ⇒ Solo per carichi equilibrati.
La prima parte del problema, ovvero il valore della tensione concatenata, è semplicemente risolubile
in quanto si conoscono la potenza e la corrente:
PCARICO = W1 + W2 = 1430 + 195 = 1625 W

Q CARICO = 3 ⋅ (W1 − W2 ) = 3 ⋅1235 = 2139 VAr
 2139 
ϕ = arctg
 = 52,77° ⇒ cos(ϕ) = 0,605
 1625 
1625
P
=
= 387,72 V
P = 3 ⋅ V ⋅ I ⋅ cos(ϕ) ⇒ V =
3 ⋅ I ⋅ cos(ϕ )
3 ⋅ 4 ⋅ 0,605
Rifasamento: chiamando Qrif la potenza reattiva dopo il rifasamento e ricordando che i condensatori
non variano la potenza attiva assorbita risulta che:
Q rif = P ⋅ tg[ar cos(0,9)] = 787,0 VAr
Q C = Q − Q rif = 2139 − 787 = 1352 VAr
potenza che deve essere messa in gioco dai C
QC
1352

=
= 9,55 µF
3 ⋅ V132
1
C ∆ =
3 ⋅ V132 ⋅ ω 3 ⋅ (387,72)2 ⋅ 314
=
⇒ 
XC =
QC
ω⋅C
C = 3 ⋅ C = 3 ⋅ 6,76 = 28,65 µF
∆
 Y
3
Scheda N° 14 - Sistemi trifase
Guasto: il circuito si trasforma in un monofase come si può vedere nelle figure seguenti.
La soluzione sembrerebbe dipendere dal collegamento del carico: stella o triangolo.
Come prima cosa dimostriamo che in entrambi i casi l’impedenza equivalente è indipendente dal tipo
di collegamento.
Collegamento a stella.
ZY
Con riferimento alla figura di sinistra si può notare che le
impedenze attraversate dalla corrente sono due e tra loro in serie
pertanto: Z EQY = 2 ⋅ ZY
IG
V31
ZY
ZY
Collegamento a triangolo.
Osservando la figura di destra si nota che tutte e tre le impedenze
sono attraversate da corrente e formano un parallelo e una serie
pertanto:
2
Z EQ∆ = (Z ∆ + Z ∆ ) / / Z ∆ = Z ∆
3
Z∆
V31
Z∆
Z∆
Ora sappiamo che poiché i due circuiti trifasi originali (non guasti) erano uguali deve sussistere la
Z
relazione Z Y = ∆ che confrontata con le precedenti implica che Z EQY = Z EQ∆ ovvero partendo
3
da due circuiti trifasi con le stesse caratteristiche (tensioni e correnti) le condizioni che si ottengono
per interruzione di una linea sono identiche sia che il carico fosse a stella sia che il carico fosse a
triangolo.
Per semplicità si farà riferimento al collegamento a stella.
Dal sistema trifase si sa che:
V
Z Y = 13
I⋅ 3
Dal monofase ottenuto dal guasto si ricava che:
V
V ⋅I⋅ 3
3
3
=
I guasto = 13 = 13
I=
4 = 3,464 A
2 ⋅ ZY
2 ⋅ V13
2
2
W2 = 0 W
W1 = V13 ⋅ I guasto ⋅ cos(ϕ ) = 387,72 ⋅ 3,464 ⋅ 0,605 = 812,5 W
4
(il ϕ è determinato dalla ZY)
Scheda N° 14 - Sistemi trifase
ESERCIZIO 14.3
Ad una linea trifase alimentata con una tensione concatenata alternata di 3 kV viene collegato un
carico che assorbe una potenza attiva (P1) pari a 200 kW e una potenza reattiva di tipo (Q1) induttivo
pari a 200 kVAr, sapendo che le perdite dovute alla linea (PL) sono pari al 5% della P1, determinare
la resistenza di linea e il cos(ϕ) del carico. Successivamente viene chiuso un tasto che collega alla
stessa linea un secondo carico parallelo al primo; insieme viene collegata una batteria di condensatori
di rifasamento. In questa nuova configurazione si conosce la potenza attiva assorbita dal secondo
carico (P2) che è pari a 80 kW e la potenza apparente assorbita dallo stesso (A2) che è di 100 kVA.
Sapendo che collegando il secondo carico la corrente di linea non varia ma rimane costante, si vuole
quindi sapere a quanto ammontano le perdite di linea nel secondo caso, il cos(ϕT) dell’intero carico e
la capacità dei condensatori.
Il circuito in fase di studio può essere rappresentato come in figura.
1
V
I1
2
IC
I2
3
T
T aperto
Quando l’interruttore T è aperto viene collegato solo il primo carico di cui conosciamo sia la potenza
attiva sia quella reattiva e risulta pertanto immediato il calcolo dello sfasamento.

 200 ⋅103  

 Q 
 = 0,707
cos(ϕ ) = cos  tg −1  1   = cos  tg −1 
3 
P


200
10
⋅

 
1




Sapendo che la potenza assorbita dalla linea è una frazione di quella assorbita dal carico è facile
trovare la prima, anche se per determinare le resistenza della linea è necessario conoscere la corrente
di linea che si può trovare note la tensione concatenata e la potenza del carico.
P1
200 ⋅103
I1 =
=
= 54,43 A
3 ⋅ V ⋅ cos(ϕ1 )
3 ⋅ 3 ⋅103 ⋅ 0,707
PL = P1 ⋅ 5% = 10 kW
RL =
PL
3 ⋅ I1
2
=
⇒
10000
3 ⋅ (54,43)
2
η=
= 1,125 Ω
5
200
= 95,24 %
210
Scheda N° 14 - Sistemi trifase
T chiuso
Per ipotesi chiudendo l’interruttore T la corrente di linea non deve cambiare in modulo. A prima
vista questo può sembrare illogico pensando che aggiungiamo un carico supplementare che assorbe
altra potenza e quindi altra corrente rispetto al primo caso con l’interruttore aperto ma può essere
più
facilmente
compreso
facendo
riferimento ad un grafico polare come
IC
quello riportato in figura. Si vede come i
condensatori, diminuendo lo sfasamento,
abbassino la corrente di linea e quindi
migliorino anche il rendimento della linea.
Poiché la corrente non varia le perdite
della linea rimangono uguali al caso
precedente però migliora il rendimento in
E
I2
quanto
aumenta
il
denominatore
ITOT
rappresentato dalla potenza totale del
carico:
PT = P1 + P2 = 200 + 80 = 280 kW
η=
I1
280
= 96,55 %
290
Il fatto che la corrente di linea non cambi implica anche che la potenza apparente non cambi (in
quanto funzione solo di tensione e corrente ma non dello sfasamento). Questo fatto ci permette di
calcolare la potenza reattiva generata dai condensatori di rifasamento in quanto i dati che abbiamo ci
permettono di trovare la potenza apparente totale (AT),la potenza reattiva del secondo carico (Q2) e
la potenza reattiva totale (QT).
A T = 3 ⋅ I1 ⋅ V = 3 ⋅ 54,43 ⋅ 3000 = 282,84 kVA
Q 2 = A 2 2 − P2 2 = 100 2 − 80 2 = 60 kVAr
Q T = A T 2 − PT 2 = 282 ,84 2 − 280 2 = 40 kVAr
Q COND = Q T − Q1 − Q 2 = 40 − 60 − 200 = 220 kVAr
A questo punto risulta semplice calcolare sia lo sfasamento totale sia la capacità dei condensatori
ipotizzando una frequenza di 50 Hz:
Q 
ϕ T = arctg T  = 8,13°
 PT 
C∆ =
Q COND
ω ⋅ V2
=
220 ⋅1000
314 ⋅ 3000 2
= 0,0000778 = 77,9 µF
6
Scheda N° 14 - Sistemi trifase
La caduta di tensione industriale
Nell’esercizio appena svolto si è fatta l’ipotesi che la corrente rimanesse costante a causa del
rifasamento. Questa ipotesi ci ha semplificato notevolmente i calcoli. Ogni linea elettrica si comporta
come una resistenza ed una induttanza in cui l’unica grandezza costante risulta essere la tensione del
generatore che si trova a monte della linea pertanto la tensione a cui i carichi sono sottoposti dipende
dalla caduta di potenziale che avviene sulla linea e perciò dalla corrente che circola nella linea stessa
e che a sua volta dipende dall’entità del carico applicato. Si capisce pertanto come un problema
siffatto non sia risolvibile se non in maniera iterativa, cosa poco agevole e per di più inutile in un
calcolo di prima approssimazione dove altri dati sono noti con uno scarso grado di precisione.
Il metodo della caduta di tensione industriale ci permette di stimare la caduta di tensione che avviene
sulla linea ammettendo che lo sfasamento dovuto alla linea stessa sia ininfluente ovvero facendo
riferimento al grafico in figura risulta che:
Partic. A
E0
O
A
E
ϕ
F
E B
ϕ
I*RL
jXL*I
I
r
r
∆VLINEA = E 0 − E ≅ E 0 − E
questo
è
vero
se
OD ≅ OC ovvero se ∆VLINEA < 10% E 0
Con queste ipotesi la caduta di tensione cercata è circa
AC e quindi risulta che:
F
AC = AE + EC = R L ⋅ I ⋅ cos(ϕ ) + X L ⋅ I ⋅ sen(ϕ) .
Nel monofase equivalente risulta che:
E 0 = E + I ⋅ ( R L ⋅ cos(ϕ ) + X L ⋅ sen(ϕ ))
B
Mentre nel trifase la tensione al carico vale:
V = V0 − 3 ⋅ I ⋅ R L ⋅ cos(ϕ ) + X L ⋅ sen(ϕ )
[
]
7
D
C
C
D
Scheda N° 14 - Sistemi trifase
ESERCIZIO 14.4
E’ dato un carico trifase che assorbe una corrente di 56 A con un angolo di sfasamento di 35° se
viene alimentato con una tensione concatenata pari a 4800 V.
Il collegamento è effettuato attraverso una linea lunga 12 km costituita da un cavo di sezione S = 20
mm2 avente resistività ρ = 6,5 Ω⋅mm2/km. Per calcolare la reattanza XL della linea si cortocircuita il
carico e, alimentando la rete a bassa tensione (220 V), si misura una corrente di linea di 29,8 A.
I1
W
V0
V
L
Si chiede di calcolare:
1.
2.
3.
4.
5.
l’impedenza della linea
la tensione che il generatore deve fornire a monte della rete
la caduta di tensione percentuale della linea
la potenza dissipata dalla linea stessa
la lettura del wattmetro inserito in figura
Come prima cosa calcoliamo i dati della linea utilizzando i risultati del corto circuito ovvero VCC e
ICC come riportato in figura; si nota come il “carico” sia a stella perciò le correnti di linea coincidono
con quelle di fase.
V
220
E CC = CC =
= 127 V
3
3
E
E CC = Z L ⋅ I L
⇒
Z L = CC = 4,26 Ω
IL
Icc
L
12
R L = ρ ⋅ = 6,5 ⋅ = 3,9 Ω
Vcc
S
20
RL
X L = Z L 2 − R L 2 = 4,26 2 − 3,9 2 = 1,72 Ω
XL
Per calcolare la tensione che deve essere fornita dal generatore si utilizzi la formula della caduta di
tensione industriale:
V0 = V + 3 ⋅ [ R L ⋅ cos ϕ + X L ⋅ sen ϕ ] ⋅ I = 4800 + 3 ⋅ [3,9 ⋅ 0,82 + 1,72 ⋅ 0.57] ⋅ 56 = 5205,56 V
V − V 5205,56 - 4800
∆V% = 0
=
⋅100 = 8,45 % < 10% OK
V
4800
8
Scheda N° 14 - Sistemi trifase
Non resta ora che calcolare le potenze attive P del carico e PL della linea:
P = 3 ⋅ V ⋅ I ⋅ cos(ϕ ) = 3 ⋅ 4800 ⋅ 56 ⋅ 0,82 = 381,4 kW
PL = 3 ⋅ R L ⋅ I 2 = 3 ⋅ 3,9 ⋅ 56 2 ≅ 36,7 kW
V12
Per calcolare la lettura del wattmetro è conveniente costruire il
seguente diagramma dal quale si deducono le relazioni tra gli angoli:
W = V23 ⋅ I1 ⋅ cos(α )
α = 90 − ϕ ⇒ cos(α) = sen (ϕ )
W = V23 ⋅ I1 ⋅ sen(ϕ ) = 4800 ⋅ 56 ⋅ 0,57 = 154,2 kW
30°
ϕ
α
V23
9
E1
I1