Lavoro didattico della prof.ssa Anna Baglivo
LAVORO E CONSERVAZIONE DELL’ENERGIA MECCANICA
COLLOCAZIONE
La seguente unità didattica relativa al “Lavoro” si colloca in una terza classe di un liceo
scientifico PNI all’interno di un percorso i cui contenuti possono essere sintetizzati nel
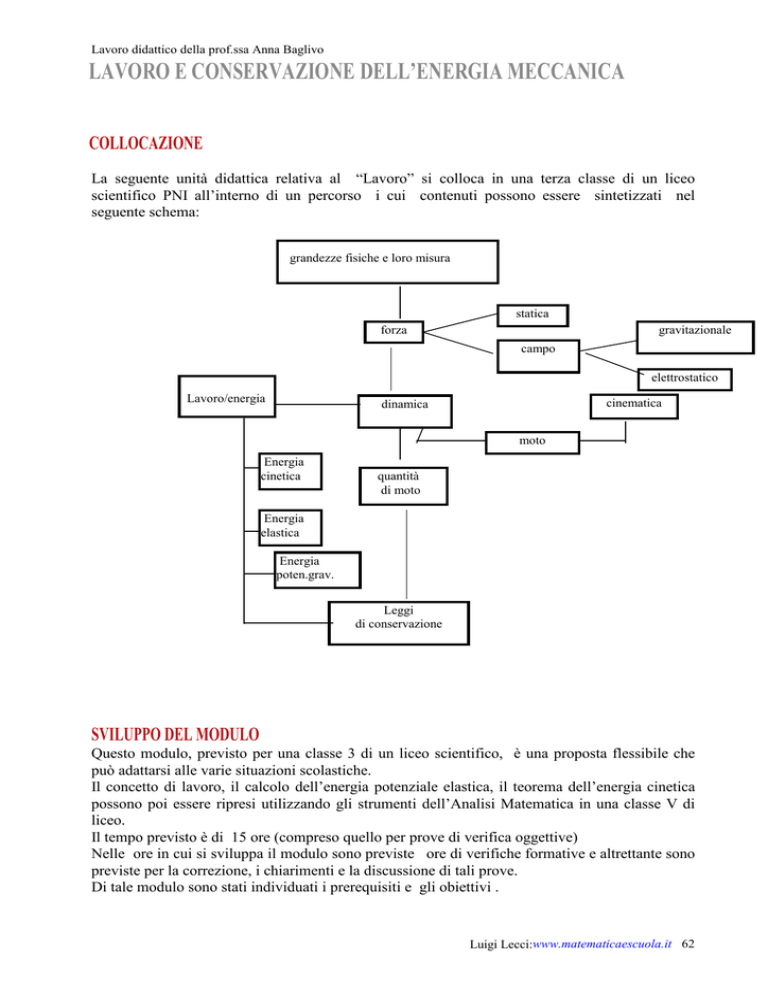
seguente schema:
grandezze fisiche e loro misura
statica
forza
gravitazionale
campo
elettrostatico
Lavoro/energia
cinematica
dinamica
moto
Energia
cinetica
quantità
di moto
Energia
elastica
Energia
poten.grav.
Leggi
di conservazione
SVILUPPO DEL MODULO
Questo modulo, previsto per una classe 3 di un liceo scientifico, è una proposta flessibile che
può adattarsi alle varie situazioni scolastiche.
Il concetto di lavoro, il calcolo dell’energia potenziale elastica, il teorema dell’energia cinetica
possono poi essere ripresi utilizzando gli strumenti dell’Analisi Matematica in una classe V di
liceo.
Il tempo previsto è di 15 ore (compreso quello per prove di verifica oggettive)
Nelle ore in cui si sviluppa il modulo sono previste ore di verifiche formative e altrettante sono
previste per la correzione, i chiarimenti e la discussione di tali prove.
Di tale modulo sono stati individuati i prerequisiti e gli obiettivi .
Luigi Lecci:www.matematicaescuola.it 62
Lavoro didattico della prof.ssa Anna Baglivo
PREREQUISITI
Conoscere le unità di misura e saper eseguire le equivalenze.
Saper impostare un'equazione dimensionale.
Rappresentare graficamente una funzione e descrivere l'andamento di un grafico.
Individuare relazioni di proporzionalità tra le variabili di una funzione.
Saper operare con i vettori.
Conoscere il concetto di forza.
Conoscere le leggi della dinamica.
Conoscere le leggi che regolano la caduta di un grave.
OBIETTIVI SPECIFICI / RISULTATI ATTESI
CONOSCENZE
Conoscere la definizione di lavoro.
Conoscere la definizione di energia cinetica e di energia potenziale.
Conoscere l'enunciato del teorema dell'energia cinetica.
Conoscere la relazione tra lavoro ed energia potenziale.
Conoscere il principio di conservazione dell'energia meccanica.
Conoscere la definizione di potenza.
COMPETENZE
Saper calcolare il lavoro compiuto da una forza.
Saper dimostrare il teorema dell'energia cinetica in alcuni casi particolari.
Saper calcolare l'energia potenziale gravitazionale ed elastica.
Saper ricavare il principio di conservazione dell'energia meccanica.
Saper applicare la definizione di potenza.
Utilizzare formule e leggi nella risoluzione di semplici problemi.
CAPACITA'
Saper scegliere gli strumenti idonei alla risoluzione di un problema.
Saper individuare concetti unificanti e modelli, mettendo in relazione fenomeni diversi
ma concettualmente uguali (concetti di lavoro, energia).
Cogliere i nodi concettuali dell’unità didattica e le mutue relazioni tra la fisica e gli altri
aspetti del sapere:– principi di conservazione (chimica, astronomia…)
Utilizzare ragionamenti di tipo induttivo e procedimenti di tipo ipotetico - deduttivo.
Saper organizzare ed eseguire esperienze di laboratorio con successiva analisi e sintesi
critica dei risultati ottenuti.
ARTICOLAZIONE DELL’UNITA’ DIDATTICA
PARTE. 1: Concetto di lavoro
Tempi previsti per questa fase didattica
2 ore di lezione per la parte teorica
2 ore e 20 minuti dedicati alla risoluzione di problemi in classe
PARTE 2: Energia
Luigi Lecci:www.matematicaescuola.it 63
Lavoro didattico della prof.ssa Anna Baglivo
Tempi previsti per questa fase didattica
2 di lezione per la parte teorica
2 ore e 30 minuti dedicati alla risoluzione di problemi in classe
PARTE 3: Legge di conservazione dell’energia meccanica
Tempi previsti per questa fase didattica
1 ora e 30 minuti di lezione per la parte teorica
2 ore dedicati alla risoluzione di problemi in classe
PARTE 4: laboratorio
Tempi previsti per questa fase didattica
1 ora e 30 minuti di lezione di laboratorio
Tempi previsti per la verifica sommativa
60 minuti
Alla fine di ogni parte (esclusa naturalmente l’ultima) è previsto di dare agli alunni delle
schede di lavoro che verranno poi corrette, commentate ed approfondite in classe; saranno
seguite da verifiche formative sia scritte che orali, al fine di accertare il livello di
apprendimento raggiunto dagli allievi, contemplando sempre attività di recupero in itinere.
METODOLOGIA SPECIFICA
Introduzione dell'argomento mediante la presentazione di una situazione o la
formulazione di una domanda che determini il bisogno di conoscere
Lezioni interattive con discussione guidate;
Lezione frontale per la sistematizzazione concettuale e la formalizzazione matematica;
verifica e valutazione
recupero e approfondimento
L’attività di laboratorio di informatica e di fisica viene utilizzata per determinare una situazione
stimolo finalizzata all’introduzione di nuovi concetti o al consolidamento di quelli già acquisiti
STRUMENTI
Libro di testo, riviste e altri libri.
Laboratorio di fisica e di informatica
Utilizzo della lavagna e della lavagna luminosa
schede di lavoro
VERIFICA E VALUTAZIONE
Si prevedono verifiche formative in itinere, finalizzate a controllare il livello di acquisizione e a
fornire elementi di:
valutazione e regolazione della proposta didattica al docente
di autovalutazione dell'adeguatezza del proprio impegno allo studente.
Le prove di verifica saranno il più possibile diversificate:
- test a risposta chiusa per controllare le conoscenze specifiche;
- risoluzione di problemi per verificare le competenze applicative;
Luigi Lecci:www.matematicaescuola.it 64
Lavoro didattico della prof.ssa Anna Baglivo
quesiti a risposta breve e stesura di brevi relazioni per verificare le capacità di
concettualizzazione;
- prove orali per verificare le capacità di esprimersi, di definire, di collegare, di cogliere
analogie e differenze.
Le competenze finali complessive verranno poi verificate mediante colloqui orali individuali
e mediante una verifica scritta (verifica sommativa)
CRITERI DI VALUTAZIONE
Per le verifiche orali si valuterà la correttezza e la completezza dei contenuti, l’uso del linguaggio
specifico, la sicurezza nell’esposizione.
Per i tests a risposta chiusa, si assegnerà un punteggio ad ogni quesito, si sommeranno i punteggi
e si elaboreranno statisticamente i risultati con i metodi stabiliti dal Dipartimento.
Per la correzione dei problemi, si terranno presenti i seguenti indicatori:
a) correttezza del procedimento risolutivo;
b) grado di completezza della soluzione:
c) correttezza nei calcoli
d) chiarezza dell’esposizione;
e) originalità del procedimento risolutivo
f) Si potrà attribuire un peso ad ogni indicatore e considerare come punteggio globale la
media ponderata dei punteggi parziali che verranno assegnati ad ogni indicatore
g) Per tutte le verifiche si fisserà comunque una soglia di accettabilità che indicherà il
raggiungimento degli obiettivi
RECUPERO
Si attiveranno iniziative di recupero:
h) in itinere
i) a fine modulo, in parallelo con l’attività di approfondimento.
j) Le attività di recupero saranno programmate, mediante esperienze di flessibilità
oraria(suddivisione di una o più classi in gruppi di livello, relativa predisposizione di
moduli di recupero) o altre modalità progettate all’interno del POF( corsi pomeridiani di
sostegno e recupero, servizio di sportello didattico).
I corsi stessi saranno finalizzati non solo al recupero delle conoscenze, ma anche al recupero
delle motivazioni, delle attese, dell’impegno e della riflessione personale, e all’acquisizione
consapevole dei processi mentali sul piano metacognitivo.
È possibile esplicitare con un procedimento a ritroso conoscenze e competenze,
evidenziandole in una mappa concettuale.
L’attività di approfondimento può consistere nella trattazione di temi specifici o nella
risoluzione di problemi complessi (per esempio problemi proposti alle olimpiadi di fisica)
CONTENUTI
Prima di iniziare a sviluppare i contenuti del modulo è bene verificarne i prerequisiti
predisponendo una prova strutturata, costituita da quesiti a risposta multipla la cui risposta
esatta non è sempre unica.
VERIFICA DEI PREREQUISITI
•
Un’automobile ha una velocità di 50 m/s. Quale delle seguenti relazioni è corretta?
a. v = 50·103 km/h b. v = 50/3600 km/h
c. v = 180 km/h
d. 50 km/h
Luigi Lecci:www.matematicaescuola.it 65
Lavoro didattico della prof.ssa Anna Baglivo
•
•
x
y
Qual è l’equazione dimensionale della forza nel S.I.?
a. [ F ] = [ ML T 2 ]
b. [ F ] = [ ML−1 T 2 ]
[
c. [ F ] = MLT −2
]
d. [ F ] = [ ML−1 T 2 ]
La grandezza y è funzione della grandezza x. Una serie di misure di x e di y ha dato il
seguente risultato:
1
2
3
4
5
3
12
27
48
75
Quale delle seguenti affermazioni è esatta?
a. y è direttamente proporzionale a x.
b. y è inversamente proporzionale a x.
c. y è proporzionale al quadrato di x.
d. y dipende linearmente da x.
•
x
y
La grandezza y è funzione della grandezza x. Una serie di misure di x e di y ha dato il
seguente risultato:
1
2
3
4
5
10,0
5,0
3,3
2,5
2,0
Quale delle seguenti affermazioni è esatta?
a. y è direttamente proporzionale a x.
b. y è inversamente proporzionale a x.
c. y è proporzionale al quadrato di x.
d. y dipende linearmente da x.
•
•
Quale delle seguenti affermazioni riguardanti il prodotto scalare di due vettori è esatta?
a. Il prodotto scalare di due vettori è uguale al prodotto dei moduli dei due vettori.
b. Il prodotto scalare di due vettori è sempre minore del prodotto dei moduli dei due
vettori.
c. Il prodotto scalare di due vettori è nullo se i due vettori sono tra loro paralleli.
d. Il prodotto scalare di due vettori è nullo se i due vettori sono tra loro perpendicolari.
Stabilire se le seguenti affermazioni sono vere [V] o false [F] e, nel caso siano false,
correggerle
a. Chiamiamo forza tutto ciò che è in grado di produrre deformazione di un corpo o
variazione di velocità. [V]
[F]
b. La forza è una grandezza scalare. [V]
[F]
c. Tutte le forze esistenti in natura possono venir ricondotte a quattro diversi tipi di
forze fondamentali.
[V]
[F]
d. Dire che la velocità di un corpo è costante significa che, se il corpo è fermo, mentre se
si muove, il moto dovrà necessariamente essere rettilineo uniforme.
[V]
[F]
e. Se su un corpo agisce una forza, la sua velocità aumenta o diminuisce. [V]
[F]
f. Il rapporto tra forza applicata e accelerazione prodotta è proporzionale alla massa del
corpo.
[V]
[F]
g. Poichè le forze che rappresentano l’interazione tra due corpi (azione e reazione) sono
uguali e contrarie, esse si annullano a vicenda. [V]
[F]
Luigi Lecci:www.matematicaescuola.it 66
Lavoro didattico della prof.ssa Anna Baglivo
PARTE 1: IL LAVORO
La struttura di questa prima parte può essere schematizzata con la seguente mappa concettuale:
Fase della motivazione
La parola “lavoro “ in fisica ha un significato talvolta diverso da quello che viene attribuito nel
linguaggio comune. Tuttavia, partendo dal concetto intuitivo di lavoro gli allievi saranno in
grado di fornire una personale risposta ai quesiti della seguente scheda di lavoro:
Cosa s'intende per Lavoro? Indicare dei fenomeni in cui viene compiuto del lavoro.
Mario deve spostare un oggetto di un tratto lungo 10m. Matteo deve spostare lo stesso
oggetto di 20m. Chi dei due fa più “fatica”?
Che cosa accade se Mario e Matteo spostano due oggetti, il primo più pesante del
secondo dello stesso tratto?
Mario e Matteo spostano l’oggetto di un stesso tratto, applicando una forza uguale. Mario
applica la forza parallelamente al suolo, Matteo applica la forza in una direzione che
forma un angolo di 60° con il suolo
Quale dei due ragazzi fa fatica maggiore?
Un uomo che sta trasporta con velocità costante una valigia lungo una piano orizzontale
liscio compie lavoro?
Si apre quindi una discussione guidata attraverso la quale dal concetto intuitivo di lavoro si
giungerà gradualmente alla definizione rigorosa di questa nuova grandezza Si cercherà inoltre di
destabilizzare le convinzioni errate che nascono dal significato che viene dato al termine lavoro
nel linguaggio ordinario.
Luigi Lecci:www.matematicaescuola.it 67
Lavoro didattico della prof.ssa Anna Baglivo
E’ intuitivo che per spostare un oggetto di un tratto ∆x si fa più fatica che per spostare dello
stesso tratto un oggetto più leggero; lo stesso oggetto richiede più fatica per essere spostato di un
tratto più lungo. Le variabili che entrano in gioco nella definizione di lavoro, quale grandezza
fisica, sono dunque: forza e spostamento.
Inoltre se si applica la spinta parallelamente al terreno con minore fatica si può ottenere lo stesso
spostamento. Al lavoro contribuisce quindi anche l’angolo che la forza forma con la direzione
dello spostamento.
Fase della sistematizzazione.
Prima di dare la definizione di lavoro è bene precisare che in fisica è sempre una forza che
compie un lavoro, anche se si è soliti dire che il giocatore, il facchino, ecc. compiono un lavoro.
Si dà inizialmente la definizione di lavoro in un caso particolare, cioè supponendo la forza
costante e supponendo che agisca nella stessa direzione dello spostamento subito dal corpo su cui
agisce la forza. In tal caso si definisce lavoro il prodotto dell'intensità F della forza per il modulo
S dello spostamento:
L=FS
Se la direzione della forza e quella dello spostamento non sono parallele ma formano un angolo
α si definirà lavoro di una forza costante il prodotto della componente F' della forza lungo la
diezione dello spostamento S per lo spostamento stesso,
cioè:
L = F' S
ma F' = F cosα, pertanto si avrà:
L = F S cosα
Tenendo presente la definizione di prodotto scalare di due vettori, il lavoro si potrà scrivere nella
forma:
L = F×S
Il lavoro di una forza costante F viene in tal modo definito come il prodotto scalare della forza
per lo spostamento, ed è perciò una grandezza scalare.
Dimensionalmente:
[ L] = [ F ][ S ] = [ MLT −2 L] = [ ML2 T −2 ]
e l'unità di misura nel S.I. che è il joule, definito come:
1 joule = 1 N m
Analizzando la formula L = F S cosα si osserva che se F è perpendicolare allo spostamento,
essendo cosα = 0 risulta:
L = 0,
se invece F è parallela allo spostamento, poichè cosα = 1 si ha:
L = F S,
Il lavoro di una forza è quindi massimo in valore assoluto quando la forza è parallela allo
spostamento ed è nullo quando la forza è perpendicolare allo spostamento. A seconda della
direzione relativa di forza e spostamento, il lavoro può essere positivo o negativo; il lavoro
positivo viene detto lavoro motore, in quanto l'applicazione della forza produce il moto del
corpo o un'accelerazione se esso è già in moto: la forza viene detta forza motrice. Il lavoro
negativo viene invece detto lavoro resistente e la corrispondente forza, forza resistente, in
quanto si oppone al moto.
Quando un sasso cade a terra è la forza di gravità che compie un lavoro motore perché agisce sul
sasso nello stesso verso dello spostamento. Quando invece il sasso viene sollevato ad una altezza
h da terra la nostra forza compie un lavoro motore mentre la forza peso compie un lavoro
Luigi Lecci:www.matematicaescuola.it 68
Lavoro didattico della prof.ssa Anna Baglivo
resistente; quando si comprime una molla, la forza elastica della molla compie un lavoro
resistente che tende a riportarla in condizioni di riposo. Le forze di attrito compiono sempre un
lavoro resistente perché si oppongono al moto.
Così, la forza F1 avente componente nello stesso verso dello spostamento S , compie lavoro
motore; mentre le forze F2 , con componenti in verso opposto allo spostamento, compie lavoro
resistente. In generale, il lavoro è positivo se l'angolo α è acuto, mentre è negativo se α è ottuso.
A questo punto si può riprendere in considerazione la scheda fornita all'inizio della lezione ed
osservare che un uomo che trasporta una valigia a velocità costante senza alzarla né abbassarla
non compie lavoro lungo un piano orizzontale liscio, non compie lavoro poichè la forza che
applica (opposta alla forza peso) è perpendicolare allo spostamento (lungo la direzione
orizzontale non agisce alcuna forza perchè l’uomo si muove con velocità costante); ciò è in
contrasto col senso comune in quanto l'uomo si stanca cioè fa "fatica". Relativamente
all’esempio della scheda si osserva anche che la forza applicata da Mario compie lavoro
maggiore rispetto a quella applicata da Matteo, ma Matteo fa maggiore fatica poichè sfrutta solo
una parte della forza che applica. Si nota quindi che non sempre il concetto intuitivo di lavoro
coincide col concetto fisico
Verifica formativa
La verifica di questa fase può essere effettuata richiedendo di
calcolare il lavoro di una forza costante se forza e spostamento hanno la stessa direzione
calcolare il lavoro di una forza costante se forza e spostamento hanno direzioni diverse
Attività guidata
Saranno corretti e discussi gli esercizi assegnati
A questo punto ci si chiede come si può determinare il lavoro nell'ipotesi in cui la forza non sia
costante.
Si può affrontare il problema dal punto di vista grafico.
Scheda stimolo
1)Calcolare il lavoro della forza peso quando un corpo cade sulla terra da un’altezza h
Rappresentare il lavoro in un grafico (F,s).
5 N se s<4m
2)Data la forza F=
10 N se s>= 4m
Trovare il lavoro che compie la forza F per spostare un corpo di 7m a partire dal punto O
3)Calcolare il lavoro che occorre compiere per comprimere una molla di un tratto x partendo
dalla posizione di equilibrio
Commento del docente
Per distanze prossime alla superficie terrestre, la forza di gravità si mantiene
costante e vale mg; pertanto il suo grafico nel diagramma
forza – spostamento è una retta parallela all’asse degli spostamenti.
Il lavoro compiuto dalla forza peso è uguale a mgh e coincide col l’area del
rettangolo avente base h e altezza F=mg .
Luigi Lecci:www.matematicaescuola.it 69
Lavoro didattico della prof.ssa Anna Baglivo
Indicando con L1 = 5*4J il lavoro per spostare il corpo dei
primi 4 m e con
L2 =10*3 J il lavoro compiuto per spostare il corpo dei
successivi 3m si ha:
L= L1+ L2
Cioè il lavoro coincide con l’area rappresentata in figura.
Il risultato ottenuto si può estendere ad una forza variabile.
In tal caso si suddivide lo spostamento in spostamenti
infinitesimi ∆Si in modo che, in ognuno di essi la forza si
possa ritenere costante.
Il lavoro compiuto dalla forza Fi nello spostamento ∆Si è
∆Li = Fi × ∆Si e il lavoro totale sarà dato da:
n L = ∑ Fi ⋅ ∆S i
i =i
Nel caso di una forza variabile solo in modulo, ma con verso e
direzioni costanti (come accade per la forza elastica di una
molla e per la forza di attrito su un percorso con coefficiente di
attrito variabile da punto a punto), la relazione precedente si
può scrivere:
n
L = ∑ Fi ∆Si
i =1
Supponiamo di conoscere la legge F(x) secondo cui varia il
modulo della forza in funzione di x e che il grafico di F(x) sia
quello rappresentato in figura.
Si suddividiamo l’intervallo x2 – x1 in un numero N, sufficientemente grande, di intervallini.
in ogni intervallo ∆ xi la forza costante si può ritenere costante e si può considerare come valore
della forza la media aritmetica tra il valore F' all'inizio di ∆xi e il valore F’’ alla fine dello stesso
intervallo. Si avrà Li = Fi ∆xi, che rappresenta l’area di un rettangolo di lati Fi e ∆xi , area che
differisce di pochissimo da quella sottesa dal tratto di curva corrispondente; se le strisce in cui si
è suddivisa l’area della figura sono infinitamente strette; gli archi di curva si possono
approssimare a dei segmenti , le due aree sono uguali e la differenza è addirittura nulla.
Solo in tal caso si può affermare che il lavoro compiuto dalla forza F nello spostamento del corpo
dal punto di ascissa x1 a quello di ascissa x2 è misurato dall’area compresa tra la curva, l’asse x
e dalle rette x = x1 ed x = x2 .
Si è utilizzato per il calcolo del lavoro un procedimento elementare, ma piuttosto
laborioso; il calcolo del lavoro può essere ripreso utilizzando un concetto
matematico più semplice da usare: l’integrale definito.
Consideriamo un corpo che si muova sotto l’azione di una forza F lungo una traiettoria qualsiasi
dal punto A al punto A’ .sia AA’= dr. Il lavoro elementare dL=Fx dr = Fds cosα = FT ds
essendo FT la componente della Forza lungo la direzione tangente alla traiettoria e ds il modulo
dello spostamento infinitesimo. Il lavoro per andare dal punto A al punto B è allora:
LAB =
∫
B
A
dL =
∫
B
A
B
F × dr = ∫ FT ds
A
Luigi Lecci:www.matematicaescuola.it 70
Lavoro didattico della prof.ssa Anna Baglivo
Questa interpretazione del lavoro come area è utile per il calcolo del lavoro di forze non costanti,
come ad esempio la forza elastica.
Come applicazione di quanto appena affermato si può far calcolare in classe agli alunni il lavoro
compiuto dall’esterno per deformare una molla di un tratto ∆x .
La forza elastica è espressa dalla legge di Hooke: F = -kx, la forza esercitata dall’esterno per
deformarla sarà kx. Nel piano cartesiano è rappresentata da una retta passante per l’origine.
Il lavoro che si deve compiere è dato dall’area del triangolo OAB, cioè:
O B ⋅ AB xF 1
1
=
= xkx = kx 2
2
2
2
2
Il lavoro compiuto dalla forza elastica -kx sarà di segno opposto:
L=
kx 2
L=−
2
A questo punto dopo aver parlato del lavoro è bene far notare
che
in molti casi è di scarso interesse conoscere il lavoro prodotto da una macchina, ma è più
importante sapere in quale intevallo di tempo tale lavoro viene compiuto. Quindi bisogna
introdurre una nuova grandezza fisica: la potenza.
Si definisce potenza media Pm di una macchina il rapporto tra il lavoro ∆L compiuto e
l’intervallo di tempo ∆t nel quale esso viene compiuto, cioè:
∆L
Pm =
∆t
Si definisce potenza istantanea P di una macchina il valore limite a cui tende la potenza media
quando l’intervallo di tempo ∆t tende a zero, cioè:
∆L
P = lim
∆t → 0 ∆t
La potenza rappresenta la rapidità con cui viene compiuto un dato lavoro.
L’ultima relazione scritta in certi casi può essere posta in una forma più comoda; infatti,
ricordando la definizione di lavoro e indicando con Fs la componente della forza che produce il
lavoro ∆L nella direzione dello spostamento, si ha:
Fs ∆S
∆S
= Fs lim
= Fs v
∆t → 0 ∆t
∆t → 0 ∆t
L’equazione dimensionale della potenza è:
P = lim
[ P] = [ LT −1 ] = [ ML2 T −2 T −1 ] = [ ML2 T −3 ]
L’unità di misura nel S.I. è il watt, cioè:
1W = 1
J
.
s
Dalla definizione di potenza si ricava che: L = P t da cui si ricava un’altra unità pratica di misura
del lavoro, il kilowattora ( kWh ), definito come il lavoro prodotto in un’ora nel caso che la
potenza fornita risulti 1 kW. Si ha:
1kWh = 103 W 3600 s = 3,6 106 J
Verifica formativa
Si somministra una verifica composta da test a risposta multipla per verificare il processo di
insegnamento-apprendimento. Si prevedono circa 20 minuti per tale verifica, dopo di che si passa
all’autocorrezione e, quindi, si procede con il chiarimento dei concetti che non sono stati
acquisiti pienamente dagli alunni. Infine si propongono alcuni esercizi da risolvere alla lavagna
Luigi Lecci:www.matematicaescuola.it 71
Lavoro didattico della prof.ssa Anna Baglivo
(per esempio si può calcolare il lavoro contro le forze di attrito per spostare un oggetto su una
superficie scabra con coefficiente di attrito variabile punto per punto)
Proponiamo ora il seguente esercizio che verrà svolto dal docente in classe riguardante questa
prima parte:
ESERCIZIO
(Un convoglio poco sicuro)
Una macchina deve trainare due rimorchi A e B di massa mA=350Kg e mB=150Kg, legati tra
loro con un cavo di acciaio di massa trascurabile su una strada asfaltata sulla quale il coefficiente
di attrito volvente è 0,005. La macchina trainante ha massa 1200Kg. Il rimorchio A è agganciato
direttamente alla macchina trainante. Trascurando la resistenza dell’aria, risolvere i seguenti
quesiti.
1.1
Il convoglio inizialmente è fermo. La macchina esercita una forza F1 costante per otto
secondi che consente al convoglio di raggiungere la velocità di 10m/s, quindi il convoglio
prosegue con velocità costante. Determinare l’accelerazione del convoglio ed il lavoro
sviluppato dal motore della macchina nella fase di accelerazione nell’ipotesi che il moto
avvenga su un piano orizzontale.
1.2
Determinare la tensione cui è sottoposto il cavo di acciaio durante la fase
dell’accelerazione e durante il moto rettilineo uniforme.
1.3
Determinare la potenza sviluppata dal motore della macchina allorché il convoglio sale su
una strada inclinata di 25° sul piano orizzontale alla velocità di 24Km/h. Determinare le
forze che agiscono sul rimorchio A e la tensione del cavo di acciaio.
Soluzione
Durante la fase di accelerazione la velocità passa da 0m/s a 10m/s; considerato che ciò si
1.1
verifica in 8s il convoglio si muove con accelerazione di modulo
∆V 10m / s
a=
=
= 1, 25m / s 2 .
∆t
8s
Calcolo dello spostamento in fase di accelerazione
Tenendo presenti le leggi del moto uniformemente accelerato, il valore dello spostamento
∆S 1 è
1
1
m
∆S1 = ⋅ a ⋅ ∆t 2 = ⋅1, 25 2 ⋅ (8s ) 2 = 40m
2
2
s
Calcolo dell’intensità della forza sviluppata dal motore della macchina
Il motore della macchina durante la fase dell’accelerazione deve sviluppare la forza F1
che deve vincere le forze di attrito che si oppongono al sistema e imprimere allo stesso
l’accelerazione a=1,25m/s2.
La forza d’attrito, considerato che il moto avviene su un piano orizzontale, è data dal
prodotto del peso complessivo del sistema dei tre corpi per il coefficiente di attrito
volvente.
Quindi
att .
att .
att .
F att = Fauto
+ Frim
. A + Frim. B = ( m + m A + mB ) ⋅ g ⋅ µV
m
F att = (1200 + 350 + 150) Kg ⋅ 9,81 2 ⋅ 0, 005 ≈ 83, 4 N
s
Applicando la seconda legge della dinamica si evince che la differenza tra F1 e la forza
d’attrito uguaglia il prodotto della somma delle masse dei tre corpi per l’accelerazione.
Dunque possiamo scrivere
Luigi Lecci:www.matematicaescuola.it 72
Lavoro didattico della prof.ssa Anna Baglivo
F1 − F att = (m + mA + mB ) ⋅ a ⇒ F1 = (m + mA + mB ) ⋅ ( g ⋅ µV + a ) =
1700 Kg ⋅ (9,81m / s 2 ⋅ 0, 005 + 1, 25m / s 2 ) = 2208, 4 N
Calcolo del lavoro sviluppato dal motore in fase di accelerazione
Poiché il motore applica la forza F1=2208,4N per un tratto lungo 40m, il lavoro compiuto
è
L1 = F1 ⋅ ∆S1 = 2208, 4 N ⋅ 40m = 88336 J
1.2
Calcolo della tensione del cavo di acciaio
Il cavo d’acciaio è soggetto alla tensione T che permette di imprimere l’accelerazione al
rimorchio B. Questa forza deve vincere anche la forza d’attrito che incontra il rimorchio.
Dunque deve risultare
att .
T − Frim
. B = mB ⋅ a ⇒ T = mB ( g ⋅ µV + a ) =
150 Kg ⋅ (9,81 ⋅ 0, 005 + 1, 25)m / s 2 = 194,9 N
Calcolo della tensione durante il moto rettilineo uniforme
Durante questo moto il cavo d’acciaio è soggetto solo alla tensione che serve per vincere
la forza di attrito incontrata dal rimorchio. Infatti, questo procede con velocità costante.
Dunque
T ' = mB ⋅ g ⋅ µV = 150 Kg ⋅ 9,81m / s 2 ⋅ 0, 005 = 7, 4 N
Occorre determinare la forza sviluppata dal motore della macchina.
Nel moto sul piano inclinato, su ciascun corpo, nella direzione del moto, agiscono la forza
d’attrito e la componente della forza peso del corpo (parallela al piano inclinato). Il
modulo della forza F complessiva che deve sviluppare il motore è dunque uguale alla
somma delle forze d’ attrito con la somma delle componenti delle forze peso lungo la
direzione del moto. Con α=25° si ha:
P// = (m + mA + mB ) g ⋅ senα ; Fatt . = µV ⋅ (m + mA + mB ) g ⋅ cos α ⇒
m
F = P// + Fatt . = 1700 Kg ⋅ 9,81 2 ( sen 25° + 0, 005 ⋅ cos 25°) ≈ 7123, 6 N
s
Calcolo della potenza sviluppata dal motore
La potenza sviluppata dal motore in un certo intervallo di tempo per definizione è uguale
al rapporto tra il lavoro sviluppato e la misura dell’intervallo di tempo in cui tale lavoro è
stato compiuto. Il valore della potenza si può anche determinare direttamente
moltiplicando il valore della forza applicata con l’intensità del modulo della velocità ( del
convoglio). Infatti, considerato un tratto di strada di misura ∆s, il tempo necessario a
percorrerlo con velocità costante di modulo V è ∆t=∆s/V; detta F la forza applicata ( dal
motore della macchina) nella direzione e nello stesso verso dello spostamento, il lavoro
prodotto è
Lavoro = F ⋅ ∆s = F ⋅ V ⋅ ∆t
e quindi la potenza sviluppata è
Lavoro F ⋅ V ⋅ ∆t
Potenza = W =
=
= F ⋅V ⇒
∆t
∆t
Km
1000m
W = 7123, 6 N ⋅ 24
= 7123, 6 N ⋅ 24 ⋅
≈ 47, 5 Kw
h
3600 s
Forze che agiscono sul rimorchio A
Sul rimorchio A agiscono le seguenti forze:
La fora F1 trainante esercitata dalla macchina.
La forza di attrito Fatt=µV⋅mAg⋅cosα, parallela al piano del moto e diretta nel verso
opposto allo spostamento del convoglio.
Luigi Lecci:www.matematicaescuola.it 73
Lavoro didattico della prof.ssa Anna Baglivo
La componente del peso del rimorchio lungo la direzione del piano inclinato; il
verso di questa forza è opposto al verso del moto (quindi verso la base del piano):
PA// = mA g ⋅ senα .
La tensione T esercitata dal cavo dovuta al trascinamento del rimorchio B da parte
del rimorchio A. La tensione T è parallela al piano del moto e diretta dal
rimorchio A al rimorchio B.
La forza di reazione vincolare esercitata dal piano d’appoggio in virtù della quale
il rimorchio poggia sul piano.
Relativamente alle forze che agiscono sul rimorchio B, fra i moduli delle componenti
lungo il piano del moto sussiste la seguente relazione:
F1 − Fatt . − PA// − T = 0
Calcolo della tensione del cavo
La tensione T è la forza che permette la salita del rimorchio sul piano inclinato. Poiché il
moto avviene a velocità costante, il modulo della tensione è uguale alla somma della
forza d’attrito esercitata dalla strada con la componente della forza peso del rimorchio B
parallela al piano. Quindi:
T = µV ⋅ mB g ⋅ cos 25° + mB g ⋅ sen 25° = mB g ⋅ ( µV ⋅ cos 25° + sen 25°) ≈628,6N
PARTE 2: ENERGIA
La struttura di questa seconda parte può essere schematizzata con le seguenti mappe concettuali:
Luigi Lecci:www.matematicaescuola.it 74
Lavoro didattico della prof.ssa Anna Baglivo
Che cosa si intende per energia?
Nel linguaggio comune si dice che ha energia una persona dinamica, sempre in movimento,
capace di svolgere una grande mole di lavoro di qualunque genere: fisico, intellettuale, ecc..
La definizione di energia che possiamo fornire è l’attitudine di un corpo di produrre lavoro.
Luigi Lecci:www.matematicaescuola.it 75
Lavoro didattico della prof.ssa Anna Baglivo
La parola “energia”, infatti deriva dal greco energeia che a sua volta deriva da ergon , “lavoro”.
L’energia di un oggetto è dunque la quantità di lavoro che esso è in grado di sviluppare; energia
e lavoro devono dunque essere omogenee cioè l’energia è misurata in fisica con la stessa unità
del lavoro, cioè il joule nel S.I.
Il concetto di energia fu introdotto nella scienza all’inizio ‘800 dal fisico inglese Thomas
Young(1773-1829), ma fu solo verso la metà del secolo che si arrivò a una chiara comprensione
dell’importanza di questo concetto, in seguito agli esperimenti e le speculazioni di tutta una serie
di giovani scienziati come Sadi Carnot (1796-1832), Hemann von Helmholtz (1821-1894),
Robert Mayer (1814-1878), J. Prescott Joule ( 1818-1889), che in modo indipendente l’uno
dall’altro arrivarono a stabilire la legge di conservazione dell’energia. Da allora, in poco tempo,
il concetto di energia è diventato uno dei pilastri fondamentali della fisica per la grande varietà
di fenomeni capaci di produrre lavoro (moto materiale, calore, suono, luce, elettricità,
magnetismo, ecc.) dei quali il principio di conservazione dell’energia fornisce un quadro
unificatore. Infatti, tutti questi fenomeni sono riconducibili e misurabili in termini di energia,
energia presente in natura in quantità assoluta costante, sebbene mascherata in una pluralità di
forme intercambiabili, per cui la scomparsa di energia di un certo tipo è sempre accompagnata
dalla comparsa di una uguale quantità di energia di tipo diverso.
L’energia si manifesta in diverse forme, in questa fase si parlerà di due tipi fondamentali di
energia meccanica: l’energia cinetica e l’energia potenziale.
Fase della motivazione
Per introdurre l’energia cinetica si possono esaminare semplici fenomeni della vita quotidiana:
un urto tra automobili è tanto più violento quanto maggiore è la velocità d’impatto; urtare con lo
scooter contro una automobile produce danni maggiori che urtare un altro scooter alla stessa
velocità. Da queste considerazioni elementari si deduce che l’energia cinetica è energia di
movimento , ed è il lavoro che può compiere un corpo di massa m movendosi a velocità v.
Fase della sistematizzazione
Consideriamo un corpo di massa m che sotto l’azione di una forza costante F subisce uno
spostamento ∆S .
Il lavoro compiuto sul corpo, supponendo che F e ∆S siano paralleli e tenendo conto del 2°
principio della dinamica, è:
L = F ∆S = m a ∆S
Se la forza viene applicata tra gli istanti t1 e t2 si ha:
v 2 − v1
a=
t 2 − t1
e il lavoro si potrà scrivere:
v2 − v1
∆S
∆S
L=m
∆S = m( v2 − v1 )
= ma
= v = m( v2 − v1 ) v
t 2 − t1
∆t
∆t
dove v è la velocità media nell’intervallo (t1,t2).
v1 + v 2
Si può pertanto scrivere v =
e, sostituendo nella relazione precedente, si ricava:
2
( v2 + v1 ) 1 2 1 2
L = m( v2 − v1 )
= mv2 − mv1
2
2
2
Chiamando energia cinetica la quantità:
1
K = mv 2
2
il lavoro si può scrivere come segue:
Luigi Lecci:www.matematicaescuola.it 76
Lavoro didattico della prof.ssa Anna Baglivo
L = K2 - K1
o anche
L = ∆K
dove L è il lavoro compiuto dalle forze esterne e ∆K è la variazione di energia cinetica del corpo
in esame.
La relazione trovata tra lavoro ed energia costituisce il Teorema dell’energia cinetica, il quale
afferma che:
Il lavoro compiuto su un corpo uguaglia la variazione di energia cinetica del corpo stesso.
In altri termini il lavoro è la quantità di energia che può essere trasformata in un fenomeno da
una forma in un’altra.
Si osserva che se L>0 risulta ∆K>0, cioè se sul corpo viene compiuto lavoro positivo (motore) la
sua energia cinetica aumenta, mentre se L<0 risulta ∆K<0, cioè se il lavoro è negativo
(resistente), l’energia cinetica del corpo su cui esso viene compiuto diminuisce, cioè il lavoro
viene compiuto a spese dell’energia cinetica del corpo.
L’energia cinetica è una tipica forma di energia dei corpi in movimento: infatti, se un corpo è in
quiete (v=0) risulta K=0, cioè non possiede energia cinetica.
Anche il teorema dell’energia cinetica può essere ripreso in una classe V dopo aver trattato il
calcolo integrale. Infatti :
Consideriamo un corpo che si muova sotto l’azione di una forza F lungo una traiettoria qualsiasi
dal punto A al punto B .Risulta:
B
B
B
B
B
B
1
1
dv
ds
LAB = ∫ dL = ∫ F × dr = ∫ FT ds = ∫ m ds = ∫ m dv = m ∫ vdv = mvB2 − mv A2 A
A
2
2
dt
dt
A
A
A
A
Attività guidata
Verranno proposti e risolti problemi che richiedano l’applicazione dell’espressione del lavoro e
dell’energia cinetica.
Altri esercizi verranno assegnati come lavoro da svolgere a casa.
ENERGIA POTENZIALE
Il teorema dell’energia cinetica afferma che il lavoro compiuto su un corpo da forze esterne è
uguale alla variazione di energia cinetica.
Immaginiamo allora di sollevare lentamente un corpo da terra portandolo ad una quota z1 in
modo che la sua velocità resti costante, oppure di comprimere lentamente una molla vincolata ad
una estremità. Abbiamo compiuto un lavoro, ma non osserviamo variazioni di velocità degli
oggetti considerati.
Siamo di fronte allora ad una nuova forma di energia che non è legata al movimento, ma alla
nuova posizione dei corpi.
Il corpo sollevato da terra o la molla compressa durante il sollevamento o la compressione hanno
immagazzinato energia che viene rilasciata sotto forma di energia cinetica durante la caduta o la
estensione della molla. A questa energia, che dipende solo dalla posizione, presente come
potenziale capacità di compiere lavoro, si attribuisce la qualificazione di energia potenziale
Tale energia dipende dal fatto che in entrambi gli esempi abbiamo compiuto un lavoro sugli
oggetti contrastando una forza:quella gravitazionale e quella elastica. L’energia potenziale
immagazzinata dai corpi dipende proprio dalla presenza di queste forze che agiscono su di essi.
Per calcolare l’espressione dell’energia potenziale,si può proporre il seguente problema:
Problema
Luigi Lecci:www.matematicaescuola.it 77
Lavoro didattico della prof.ssa Anna Baglivo
Calcolare il lavoro compiuto dalla forza peso quando un corpo di massa m
cade dal punto A ad altezza hA dal suolo ad un punto B
ad altezza hB
Che cosa succede se il corpo segue il percorso ACB?
Commento del docente
Il lavoro della forza peso per spostare il corpo da A a B è:
L= mg (hA – hB ) =mg hA -mg hB
Seguendo il percorso ACB si ottiene lo stesso risultato:
Infatti, lungo il tratto AC:
L = mg lcosα= mg (hA – hB ) ) =mg hA -mg hB
lungo il tratto BC il lavoro è nullo essendo la forza
perpendicolare allo spostamento.
Si può dimostrare che il lavoro non cambia se il corpo passa da A a B, seguendo una traiettoria
qualsiasi; il lavoro compiuto dalla forza di gravità quando un corpo viene spostato dipende solo
dalla posizione iniziale e finale del corpo e non dal particolare percorso seguito.
Una forza per la quale il lavoro compiuto non dipende dal particolare percorso seguito,
ma solo dalle posizioni estreme si dice posizionale o conservativa.
Pertanto, si può rappresentare il lavoro delle forze di gravità, introducendo una funzione della
posizione, cioè l’energia potenziale di gravità ad una altezza h dal suolo
U=mgh+c
tale che si abbia;
L = UA - UB = - ∆U
con ∆U = variazione di energia potenziale tra le quote hA e hB.
Dalla relazione trovata risulta che durante il sollevamento del corpo essendo ∆U>0, sarà L<0,
ovvero le forze di gravità hanno compiuto un lavoro resistente, opponendosi al sollevamento del
corpo.
Si osserva infine che se viene attribuito convenzionalmente energia potenziale nulla al livello del
suolo, l’energia potenziale di un corpo di massa m a quota h è
U=mgh
Il lavoro calcolato precedentemente è quello compiuto dalla forze di gravità, se il lavoro viene
compiuto dall’esterno questo è: Lest = ∆U ciò significa che si ha un aumento di energia potenziale
che verrà restituita nel momento in cui si lascerà cadere l’oggetto a terra.
Attività guidata
A questo punto gli allievi dovrebbero essere in grado di trovare espressione dell’energia
potenziale elastica. Si partirà da quanto già appreso per il calcolo del lavoro per forze non
costanti cioè dal calcolo del lavoro come area.
Luigi Lecci:www.matematicaescuola.it 78
Lavoro didattico della prof.ssa Anna Baglivo
Se si vuole allungare la molla con velocità costante dalla posizione x1 alla posizione x2 bisogna
applicare una forza dall’esterno pari a F = k x; il lavoro compiuto sarà l’area del trapezio in
figura, cioè:
1
1
Lesterno = kx 22 − kx12
2
2
Il lavoro compiuto dalla molla è lo stesso, ma cambiato di segno, cioè:
1
1
Lmolla = kx12 − kx 22
2
2
Chiamando energia potenziale elastica della molla la quantità:
1
U = kx 2
2
si ha:
L = - ∆U
cioè si ritrova lo stesso risultato valido per la forza di
gravità, cioè il lavoro compiuto da una forza è uguale e
opposto alla variazione di energia potenziale del corpo
su cui la forza agisce. Si ricava, quindi, che anche la
forza elastica è conservativa.
Si può notare che la deformazione della molla compare
al quadrato, pertanto una molla allungata di un tratto x
immagazzina la stessa energia potenziale elastica di
una molla identica compressa dello stesso tratto x, tale
energia viene restituita all’esterno quando la molla è libera di tornare nella posizione di
equilibrio. C’è da notare ancora che si è convenuto di assegnare valore zero all’energia
potenziale elastica della molla a riposo, cioè per x = 0.
L’energia elastica delle molle è molto sfruttata, infatti se si comprime una molla e la si tiene
compressa con un fermo, quando la si lascia libera, essa scatta e può compiere lavoro, come
accade nelle molle degli orologi o dei giocattoli a ricarica, nei quali l’energia elastica della molla
viene utilizzata per compiere lavoro sul bilanciere o per mettere in moto un giocattolo.
Altri corpi, oltre alle molle, si comportano allo stesso modo, pur avendo configurazioni
differenti. Ad esempio, nell’arco l’energia immagazzinata durante la tensione della corda viene
impiegata per conferire energia cinetica alla freccia.
PARTE 3: LEGGE DI CONSERVAZIONE DELL’ ENERGIA
MECCANICA
Luigi Lecci:www.matematicaescuola.it 79
Lavoro didattico della prof.ssa Anna Baglivo
Mediante lezione frontale si dimostra il principio di conservazione dell’energia e se ne farà
subito una verifica sperimentale nel laboratorio di fisica.
Se si considera un corpo in movimento questo possiede energia cinetica, la cui variazione è
uguale al lavoro compiuto dalle forze agenti. Se tali forze sono conservative il corpo possiede
energia potenziale, la cui variazione cambiata di segno è uguale al lavoro compiuto dalle forze.
Quindi per il teorema dell’energia cinetica si può scrivere:
L = K2 - K1
se le forze sono conservative si può scrivere:
L = U1 - U2
confrontando le due formule si ha:
K2 - K1 = U1 - U2
cioè:
K1 + U1 = K2 + U2
Se ora chiamiamo energia meccanica totale E di un corpo la somma della sua energia cinetica e
della sua energia potenziale:
E=K+U
la relazione precedente diventa:
E1 = E2
ossia
E = K + U = costante
che costituisce il principio di conservazione dell’energia meccanica; cioè l’energia meccanica
totale di un sistema isolato soggetto a sole forze conservative si mantiene costante.
E’ fondamentale il requisito che il sistema sia isolato, in quanto in caso contrario eventuali
apporti di energia dall’esterno farebbero variare l’energia totale del sistema.
Scheda di lavoro
a) Se invece di far cadere la pallina, la si lancia verso il basso, la variazione di energia
cinetica è la stessa? Perché?
Luigi Lecci:www.matematicaescuola.it 80
Lavoro didattico della prof.ssa Anna Baglivo
b) Facendo cadere un foglio di carta aperto è valida la legge di conservazione dell’energia
meccanica?
c) Un corpo di massa 10Kg. È posto su una mensola situata a 3m. dal pavimento, il quale si
trova a 4m. dal suolo. Qual è la sua energia potenziale rispetto al pavimento e rispetto al
suolo? Cosa ti suggeriscono i risultati ottenuti?
d) Un corpo di massa 10 kg., viene lasciato cadere da un’altezza in cui si ha un’energia
potenziale di 980J. Quando giunge a terra ha una velocità di 10m/s. cade in assenza di
aria? Perché?
e) Un paracadutista che si lascia cadere da un aereo, cadendo raggiunge una velocità
massima, detta velocità limite. Quale delle seguenti asserzioni è corretta?
f) La velocità limite è raggiunta quando alla diminuzione dell’energia potenziale non
corrisponde più un aumento di energia cinetica.
g) La velocità limite è raggiunta quando qualche vincolo impedisce l’ulteriore diminuzione
dell’energia potenziale. Se sì, quale?.
h) La velocità limite viene raggiunta quando l’energia potenziale si è tutta “consumata.
La discussione delle risposte serve a sottolineare che:
La conservazione dell’energia meccanica è valida nel caso in cui non ci sia scambio di
energia tra il sistema fisico e l’esterno, cioè il sistema è isolato(nella caduta di un
corpo il sistema fisico è costituito dal corpo e la Terra)
La conservazione dell’energia è indipendente dal sistema di riferimento.
Prima di far svolgere ai ragazzi la scheda di lavoro diamo dei semplici esempi riguardanti la
conservazione dell’energia meccanica:
Consideriamo un corpo che cade lungo un piano inclinato, di lunghezza l ed altezza massima h :
Ah
AB=l
AC=h
h = l senθ
θ
C
B
Osserviamo che la componente lungo AB della forza peso compie lavoro non nullo, ossia
L = mg l senθ
⇒
L = mgh ≡ Ua
quindi il corpo in A possiede un’energia potenziale Ua pari a quella posseduta da un corpo in
caduta libera.
Forza elastica
Luigi Lecci:www.matematicaescuola.it 81
Lavoro didattico della prof.ssa Anna Baglivo
Consideriamo ora un corpo di massa m soggetto ad una forza elastica di richiamo. Sappiamo già
dalla cinematica che se lo si sposta dalla posizione di equilibrio e poi viene lasciato libero, esso
si muove di un moto oscillatorio armonico. Anche in questo caso l’energia meccanica totale, data
dalla somma dell’energia cinetica e di quella elastica, si conserva ossia:
1 m v a2 + 1 k x a2 = 1 m v a 2 + 1 k x a 2
2
2
2
2
⇒
va =
k xb
m
A
B
XA=O
XB=O
Conservazione dell’energia meccanica nel pendolo semplice:
Dopo aver richiamato dalla cinematica le proprietà del pendolo semplice, tralasciando l’attrito
con l’aria e ricordando che la tensione T del filo non compie lavoro (perché perpendicolare allo
spostamento ) possiamo schematizzare tale sistema fisico come in figura :
h
θo
θ
C
A
P
h = l – l cosθo = l ( 1- cosθo )
B
sulla massa m non agisce solo la forza peso P = mg e quindi si ha:
EP = 1 mvP2
UP = mg l – mg l cosθ
2
In particolare nei punti A e B si ha
EA = 0
UA = mgh = mg l – mg l cosθo
Luigi Lecci:www.matematicaescuola.it 82
Lavoro didattico della prof.ssa Anna Baglivo
EB = 1 mvB2
2
UB = mg hB = 0
Per il principio di conservazione dell’energia meccanica si ha
UA - UB = EB - EA
⇒
⇒
mg l – mg l cosθo = 1 m vB2
2
vB = √ 2gl ( 1-cosθo )
Luigi Lecci:www.matematicaescuola.it 83
Lavoro didattico della prof.ssa Anna Baglivo
PARTE 4: LABORATORIO
Ora ci si sposta nel laboratorio di fisica per una verifica sperimentale.
Il dispositivo illustrato nella figura accanto può essere utilizzato
per una verifica del principio di conservazione dell’energia
meccanica.
Si prende una molla scarica e la si appende verticalmente a un
sostegno segnando su un’apposita scala la posizione di equilibrio
0; poi si appende alla molla una massa nota m e si segna sulla
stessa scala la posizione 3 in corrispondenza della posizione di
equilibrio così ottenuta; la distanza x tra le due posizioni consente
di determinare la costante elastica della molla attraverso la
relazione kx = mg. Poi si solleva l’estremo inferiore della molla
con la massa m sempre appesa all’incirca a metà strada tra la
posizione 0 e quella 3 e si segna sulla scala la posizione 1, quindi
si lascia
la molla libera di oscillare verticalmente. Essa oscillerà dalla
posizione 1, corrispondente alla massima compressione, alla
posizione 2, corrispondente al massimo allungamento, posizione
che verrà segnata sulla scala. Il centro di oscillazione si troverà in
corrispondenza alla posizione di equilibrio 3.
A questo punto si può applicare il principio di conservazione
dell’energia: nella posizione 1 la molla è deformata di un tratto x0
rispetto alla posizione 0 a molla scarica; nella posizione 2 è
deformata invece di un tratto x1; in entrambe le posizioni, che sono
anche punti di inversione del moto, l’ energia cinetica della massa
m è nulla, perciò si potrà scrivere che quando la massa m passa
dalla posizione 1 a quella 2 la sua energia potenziale di gravità
diminuisce di mgh, mentre l’energia potenziale elastica della molla
1
1
deve aumentare da kx02 a kx12 . Il principio di conservazione
2
2
dell’energia richiede che le due variazioni siano uguali, cioè:
1
( k x12 − x02 = mg ( x1 − x0 ) .
2
L’esperimento consiste nel verificare la validità della relazione
precedente.
Si ripetono più volte le misure di x0 e di x1 in modo da ridurre gli
errori di misura e si assumono come valori quelli medi ricavati dalle
misure ripetute.
Si ripete poi l’esperimento cambiando il valore della massa m e
l’ampiezza delle oscillazioni.
In questa lezione si raccolgono solo i dati, nella successiva si può
andare nel laboratorio di informatica per trasferirli in un foglio
elettronico (Excel) per elaborarli ed esaminare così se è valido il
principio di conservazione dell’energia meccanica entro gli errori di
misura sperimentali.(Discutere insieme del laboratorio di informatica)
Come compito a casa si può far stilare una relazione sull’esperimento svolto.
(
)
Luigi Lecci:www.matematicaescuola.it 84
Lavoro didattico della prof.ssa Anna Baglivo
APPROFONDIMENTI
CURVE DELL'ENERGIA POTENZIALE ED EQUIPOTENZIALI
Consideriamo una palla metallica, che
rotola su una pista simile a una montagna
russa. Inizialmente la palla è ferma nel
punto A.
Poiché l'altezza nel punto A è y = h,
l'energia meccanica iniziale della palla è
Eo = mgh. Se l'attrito e le altre forze non
conservative possono essere trascurati
l'energia meccanica della palla rimane
fissata al valore Eo per tutta la durata del
suo moto. Perciò:
E = U + K = Eo
Quando la palla si muove, la sua energia
potenziale di volta in volta diminuisce e aumenta seguendo l'andamento della pista. Infatti
l'energia potenziale gravitazionale, U = mgy, è direttamente proporzionale alla quota della pista,
y. Quindi, la pista stessa rappresenta un grafico dell'energia potenziale di un oggetto che si
muove su di essa.
Ciò è mostrato chiaramente in figura a lato
L'andamento
dell’energia
potenziale U, riportata sull'asse
verticale, riproduce proprio quello
della pista della figura precedente
in cui abbiamo indicato con una
linea orizzontale il valore Eo, che
rappresenta l'energia costante della
palla. Dovendo la somma delle
energie potenziale e cinetica
essere sempre uguale a Eo segue
che K è la differenza tra l'energia
totale Eo e l'energia potenziale,
individuata sulla curva, come
rappresentato in figura .
L'analisi di un grafico dell'energia come quello della figura sopra riportata fornisce una grande
quantità di informazioni sul moto di un oggetto. Nel punto B l'energia potenziale ha il suo valore
minimo e perciò l'energia cinetica ha in quel punto il suo massimo valore. Nel punto C l'energia
potenziale è aumentata, comportando una corrispondente diminuzione dell'energia cinetica. Man
mano che la palla prosegue nel moto sulla pista, il grafico mostra che l'energia potenziale cresce
finché, nel punto D,
raggiunge di nuovo un
valore uguale all'energia
totale Eo.
In questo punto l'energia
cinetica è zero e la palla si
ferma per un istante. Quindi
«si volta» e inizia a
muoversi verso sinistra,
Luigi Lecci:www.matematicaescuola.it 85
Lavoro didattico della prof.ssa Anna Baglivo
tornando al punto A dove si ferma ancora, cambia verso e inizia un nuovo ciclo. I punti A e D
vengono chiamati punti di inversione del moto.
Osserviamo punti di inversione anche nel moto di una massa attaccata a una molla, come
mostrato in figura A, dove la massa spinta nella posizione x = A è rilasciata da ferma; in figura
1
B, invece, è mostrata l'energia potenziale del sistema, U = kx 2 . Far partire il sistema in questo
2
1 2
modo fornisce un'energia iniziale Eo = kA indicata dalla linea orizzontale. Amano a mano che
2
la massa si muove verso sinistra, il modulo della sua velocità cresce,raggiungendo un massimo
nel punto
in cui l’energia potenziale è minima, in x = 0. Se non agiscono le forze non conservative, la
massa continua verso x = -A, dove si ferma momentaneamente prima di ritornare in x = A.
FORMA GENERALE DEL PRINCIPIO DI CONSERVAZIONE DELL’ENERGIA E SUA
APPLICAZIONE ALLA RICERCA DELLA RELAZIONE TRA SPAZIO DI FRENATA E VELOCITA’
DEL VEICOLO
Nell’approfondimento si amplierà il principio di conservazione dell’energia finora visto solo per
forze conservative.
Le forze che non ammettono energia potenziale e per le quali quindi il lavoro compiuto dipende
dal particolare percorso seguito vengono dette forze dissipative. Anche per tali forze si può
enunciare una nuova forma del principio di conservazione dell’energia, che finora si è visto solo
per forze conservative. A tal fine si considera il teorema dell’energia cinetica e si indica con Lc il
lavoro delle forze conservative e con Ld quello delle forze dissipative, si ha:
L = Lc + Ld = ∆K
ma Lc = - ∆U, pertanto si ha:
L = - ∆U + Ld = ∆K
ossia:
Ld = ∆U + ∆K
o anche
Ld = ∆E
Tale relazione è una formulazione più generale del principio di conservazione dell’energia
quando su un corpo agiscono anche forze dissipative, il quale dice:
la variazione di energia meccanica totale di un corpo uguaglia il lavoro compiuto su esso dalle
forze dissipative.
Poichè le forze dissipative compiono sempre un lavoro resistente, quindi negativo si avrà sempre
una variazione di energia meccanica negativa, cioè una diminuzione di energia meccanica del
corpo su cui agiscono. Se, per esempio si considera una sferetta che scende a terra lungo un piano
inclinato scabro, l’energia potenziale, che aveva all’inizio, non verrà trasformata tutta in energia
Luigi Lecci:www.matematicaescuola.it 86
Lavoro didattico della prof.ssa Anna Baglivo
cinetica alla base del piano a causa delle forze di attrito che sono forze dissipative. Nella maggior
parte dei casi il lavoro delle forze dissipative compare sotto una nuova forma di energia detta
energia termica o calore che provoca il riscaldamento del corpo in moto.
Il principio di conservazione può essere ancora generalizzato, soprattutto in particolari fenomeni
fisici relativi al mondo microscopico se si tiene conto che la materia si può trasformare in energia
o viceversa, in base a quanto postulato dalla teoria della relatività di Einstein e verificato
sperimentalmente in molti fenomeni, cioè: E = m0c2 dove E rappresenta la quantità di energia, m0
la massa e c la velocità della luce.
Tenendo conto di tutto quello che è stato detto, il principio di conservazione dell’energia assume
la forma:
∆E + Q + m0c2 = 0
che è la più completa, in quanto tiene conto di tutte le possibili trasformazioni dall’una all’altra
forma di energia.
Come applicazione del principio di conservazione dell’energia quando si è in presenza di forze
dissipative, si può far calcolare agli studenti lo spazio di frenata di un veicolo in funzione della
sua velocità.
Per trovare tale relazione si tiene conto che:
Ld = ∆K + ∆U
se la strada è pianeggiante ∆U = 0. Poichè l’automobile si ferma si avrà: ∆K = K2 - K1 =
=0 - mv2/2 = - mv2/2.
Il lavoro delle forze di attrito è dato da: Ld = - µ m g ∆S, dove ∆S = spazio di frenata.
Quindi la relazione Ld = ∆K + ∆U si potrà scrivere:
- µ m g ∆S = - mv2/2
cioè:
v2
∆S =
. Da qui si vede che ∆S è proporzionale al quadrato della velocità.
2 µg
Luigi Lecci:www.matematicaescuola.it 87
Lavoro didattico della prof.ssa Anna Baglivo
Esercizi proposti
Lo svolgimento dei seguenti esercizi sarà proposto come preparazione al compito in classe
Sono previste domande a risposta chiusa e numerosi quesiti affinché i ragazzi possano verificare
le loro conoscenze, competenze e capacità.
CONOSCENZE
1) Quale delle seguenti affermazioni, riguardanti il lavoro di una forza applicata a un punto
materiale, è errata?
a. Il lavoro è positivo se la forza compie un lavoro motore.
b. Il lavoro è negativo se l’angolo formato dalla direzione della forza con la direzione dello
spostamento è ottuso.
c. Il lavoro è una grandezza vettoriale, in quanto sia la forza sia lo spostamento sono grandezze
vettoriali.
d. La forza centripeta non compie lavoro in quanto è costantemente normale alla direzione del
moto.
2)
Due automobili in movimento sono ostacolate da forze resistenti uguali e viaggiano a
velocità diverse v e v’. Dette P e P’ le potenze fornite dai motori, quale delle seguenti
relazioni è esatta?
b. P = P’
c. P/P’ = v/v’
d. P/P’ = v’/v
a. P = P’ = 0
3) Un corpo di massa m si muove a velocità v. Un secondo corpo di massa m/2 si muove a
velocità 2v. Se Ec ed Ec’ sono le energie cinetiche rispettivamente del primo e del secondo
corpo, possiamo affermare che sussiste la relazione:
a. Ec’ = 2Ec
b. Ec’ = Ec
c. 2Ec’ = Ec
d. Ec’ = 4Ec
4) L’energia potenziale gravitazionale di un grave lanciato verticalmente verso l’alto con velocità
v subisce un incremento massimo ∆U. Qual è l’incremento massimo dell’energia potenziale
gravitazionale, se il grave viene lanciato verticalmente verso l’alto con velocità 2v? (Si
trascuri la resistenza dell’aria.)
b. 4∆U
c. ∆U/2
d. ∆U/4
a. 2∆U
5) Per allungare una molla di costante elastica k di un tratto x si compie un lavoro L. Possiamo
affermare che per allungare una molla di costante elastica k/2 di un tratto 2x è necessario
compiere un lavoro:
a. 2L
b. L/2
c. 4L
d. L/4
COMPETENZE
6) Un uomo trascina un carrello tirando l’asta con una forza F = 30 N inclinata di 45°
sull’orizzontale; quale lavoro compie l’uomo per spostare il carrello di ∆s = 20m?
7) Se nell’esercizio precedente il coefficiente di attrito tra carrello e strada è µ = 0,1, e il carrello
ha una massa m = 15 kg, qual è il lavoro compiuto contro le forze di attrito?
8) Un oggetto viene trascinato su una superficie scabra il cui coefficiente di attrito varia
da un punto all’altro. Il grafico della forza di attrito è indicato in figura.
Calcolare il lavoro compiuto contro le forze di attrito per spostare l’oggetto da x1=2m
a x2= 5m.
9)
Un uomo vuole sollevare da terra una valigia di massa m fino ad altezza h; ricavare le
espressioni del lavoro che l’uomo deve compiere nei seguenti due casi:
Luigi Lecci:www.matematicaescuola.it 88
Lavoro didattico della prof.ssa Anna Baglivo
a. la valigia viene sollevata a velocità costante;
b. viene sollevata con accelerazione pari a quella di gravità.
10) Un’automobile avente una massa m=1000kg si muove su un rettilineo con velocità v=108
km/h. Determinare la forza costante capace di frenare l’automobile in modo da arrestarla in
uno spazio s=200m.
11) Un motore della potenza di 3 kW è capace d’innalzare in 5s un corpo a un’altezza di 15m.
Calcolare il peso del corpo.
12) Un arciere esercita una forza F=25kgf per incoccare una freccia di massa m=120g. Il centro
della corda viene spostato all’indietro di un tratto d=30cm. Trascurando la massa dell’arco e
della corda, calcolare l’energia potenziale elastica immagazzinata nell’arco teso e la velocità
con cui la freccia lascia l’arco.
13) Un corpo di massa 20g scivola senza attrito partendo da fermo dalla estremità di un piano
inclinato di 30° e lungo 9,8m. Calcolare la velocità con cui il corpo arriva sulla base del
piano e il lavoro compiuto dalla forza di gravità.
CAPACITA’
14) Una delle principali attrattive del Luna Park è il “giro della morte”, un esercizio acrobatico
nel quale un ciclista percorre una pista circolare disposta in un piano verticale: a un certo
punto il ciclista si trova a testa in giù, ma, se la velocità è abbastanza alta, esso non precipita.
Sapendo che la pista ha un raggio r=4m e trascurando gli attriti, calcolare la minima velocità
vA con la quale il ciclista deve affrontare la pista nel punto A per non precipitare.
Luigi Lecci:www.matematicaescuola.it 89
Lavoro didattico della prof.ssa Anna Baglivo
Liceo Scientifico Statale “G. Stampacchia”
Tricase
Tempo di lavoro
60 minuti
Oggetto: Compito di Fisica – Classe 3-D\PNI
Tema: Dinamica- Conservazione dell’energia- Forza d’attrito – Teorema dell’energia
cinetica- Energia immagazzinata in una molla.
Problema_1
Un trapezista ha massa 60Kg ed è agganciato ad una funicella inestensibile di massa
trascurabile lunga 5m. Il secondo estremo della funicella è agganciato al sostegno O. Il trapezista
si lascia cadere con velocità iniziale nulla dalla piattaforma collocata alla stessa altezza del punto
O rispetto al suolo.
1. Descrivere il moto del trapezista.
2. Determinare la velocità del trapezista e la tensione della funicella quanto il trapezista si
troverà sulla verticale per O.
3. Determinare la velocità del trapezista quando la funicella forma un angolo di 45° con la
verticale per O.
4. Determinare l’angolo che la funicella forma con la verticale per O quando il modulo della
velocità del trapezista è uguale alla metà del valore massimo raggiungibile.
Problema_2
Si colloca in cima ad un piano scabro, inclinato di 45° rispetto al piano orizzontale, un blocco di
legno di 2Kg. Tra le superfici a contatto sussiste un coefficiente di attrito statico µs=0,5 ed un
coefficiente di attrito dinamico
µd=0,3.
1) Verificare che il blocco
lasciato libero scende lungo
il piano.
2) Nell’ipotesi che il piano
inclinato sia lungo 76 cm,
determinare il modulo della
velocità con cui il blocco
giunge alla base del piano.
3) Una volta sul piano
orizzontale,
il
blocco
prosegue il suo moto su una
superficie liscia fino a
scontrarsi con una molla,
bloccata in un estremo,
avente costante elastica
k=200N/m . Determinare la
compressione della molla.
Luigi Lecci:www.matematicaescuola.it 90
Lavoro didattico della prof.ssa Anna Baglivo
Soluzione
Problema_1
Un trapezista ha massa 60Kg ed è agganciato ad una funicella inestensibile di massa trascurabile
lunga 5m. Il secondo estremo della funicella è agganciato al sostegno O. Il trapezista si lascia
cadere con velocità iniziale nulla dalla piattaforma collocata alla stessa altezza del punto O
rispetto al suolo.
5. Descrivere il moto del trapezista.
6. Determinare la velocità del trapezista e la tensione della funicella quanto il trapezista si
troverà sulla verticale per O.
Soluzione
1. Il problema in esame si risolve agevolmente applicando il principio di conservazione
dell’energia.
Poiché nel testo non si fa alcuna ipotesi su
eventuali attriti supponiamo che questi siano
trascurabili.
Il trapezista descriverà un moto circolare
perché è vincolato dalla funicella. La sua
distanza dal centro O di rotazione è costante.
E’ immediato riconoscere che partendo dal
punto A arriverà nel punto B collocato alla
stessa quota di A; B è il secondo estremo del
diametro della semicirconferenza di centro O.
Il moto avviene per effetto della forza
gravitazionale (forza peso del trapezista) che è conservativa e si conserva l’energia
meccanica complessiva perché sono trascurabili gli attriti. Una volta giunto in B il
trapezista ridiscenderà per ritornare in A. Il moto continuerà con le stesse caratteristiche.
Precisiamo che il modulo della velocità è variabile.
2. Poniamo uguale a zero l’energia gravitazionale sul piano orizzontale passante per il punto
L, punto più in basso per il quale passa il baricentro del trapezista (vedi figura). Poniamo
R=5m la misura della funicella.
Nella posizione A il trapezista ha velocità nulla e la sua energia potenziale gravitazionale
vale U=mgR. Quando passerà dal punto L è nulla l’energia potenziale gravitazionale e
l’energia meccanica del trapezista sarà uguale alla sola energia cinetica. Sussiste la
seguente uguaglianza
1 2
mv = mgR ⇒ v = 2 gR = 9,90ms −1
2
(1)
Calcolo della tensione della funicella nel punto L
Nella posizione L sul trapezista agiscono due forze dirette lungo la verticale: la forza peso
mg diretta verso il basso e la tensione della funicella T diretta verso l’alto. Indicata con
a l’accelerazione del trapezista nell’istante in cui passa da L, per la seconda legge della
dinamica possiamo scrivere l’uguaglianza
mg + T = ma
(2)
Dalla quale si deduce che anche l’accelerazione è diretta lungo la verticale, più
precisamente, è diretta verso il centro O (accelerazione centripeta). Possiamo scrivere la
(2) in forma scalare secondo un asse verticale orientato verso l’alto. Si ottiene:
−mg + T = ma ⇒ T = m( g + a )
(2.1)
Ricordiamo ora che in un moto curvilineo il modulo dell’accelerazione centripeta è
Luigi Lecci:www.matematicaescuola.it 91
Lavoro didattico della prof.ssa Anna Baglivo
ac =
v2
R
(3)
e tenendo conto dell’espressione (1) per il modulo della velocità lineare si può scrivere
ac =
2
v
=
R
(
2 gR
R
)
2
= 2g
Il valore della tensione T è allora
T = m( g + 2 g ) = 3mg .
Conclusione
La tensione della funicella è pari a tre volte il peso del trapezista. Sostituendo i valori alle
grandezze si ha:
T = 3 ⋅ 60 Kg ⋅ 9.81
m
≈ 1766N
s2
3. Determinare la velocità del trapezista quando la funicella forma un angolo di 45° con la
verticale per O.
In Fig.2 è indicata con C una delle due posizioni nelle quali la funicella che regge il
trapezista forma un angolo di 45° con la verticale per il centro O. Il trapezista sta
scendendo.
Nella posizione indicata il trapezista possiede energia cinetica ed energia potenziale
gravitazionale e la loro somma è uguale
all’energia potenziale gravitazionale iniziale.
Per quanto riguarda il valore dell’energia
potenziale gravitazionale residua, notiamo che
vale
U g = mg ⋅ LH = mg ( R − R cos 45° ) =
2
mgR 1 −
2
Indicando con V1 il modulo della velocità in C
sussiste l’uguaglianza
Ec + U g =
1
2
mV12 + mgR 1 −
= mgR
2
2
Risolvendo l’equazione nell’incognita V1 si ricava
V1 = gR 2 ≈ 9,81
m
m
⋅ 5m ⋅ 2 ≈ 8,33
2
s
s
4. Determinare l’angolo che la funicella forma con la verticale per O quando il modulo
della velocità del trapezista è uguale alla metà del valore massimo raggiungibile.
Il trapezista raggiunge la velocità massima quando passa per il punto L, cioè per la
verticale per il centro O di rotazione. Questo valore è stato calcolato nel quesito n.2 e
risulta
Vmax = 2 gR .
Abbiamo già precisato che il moto del trapezista è oscillatorio intorno al punto O; nella
fase di ritorno da B verso A, quando il trapezista ripasserà da una qualsiasi posizione P, la
velocità avrà lo stesso modulo della velocità posseduta nello stesso punto nella fase di
Luigi Lecci:www.matematicaescuola.it 92
Lavoro didattico della prof.ssa Anna Baglivo
“andata” mentre il verso sarà opposto. Sia P la posizione nella fase di andata da A verso
B, durante la discesa, nella quale la velocità sia Vmax / 2 . Indichiamo con P’ la proiezione
ortogonale di P sulla verticale per O e con α l’angolo formato dalla funicella con la stessa
verticale.
Il valore dell’energia potenziale gravitazione posseduta dal trapezista nella posizione P è
U g = mg ⋅ LP ' = mgR (1 − cos α )
La relazione dedotta dalla conservazione dell’energia meccanica, uguagliando l’energia
nella posizione OP all’energia iniziale posseduta in A, è:
Ec + U g =
1
1
mVP2 + mgR (1 − cos α ) = mgR ⇒ VP2 = gR cos α
2
2
Poiché deve essere
Vp =
2 gR
Vmax
gR
2
=
⇒ VP =
2
2
2
e quindi si deve verificare l’uguaglianza
1 gR
1
⋅
= gR cos α ⇒ cos α = ⇒ α ⇒ α = arccos(0, 25) ≈ 75°31'
2 2
4
Luigi Lecci:www.matematicaescuola.it 93
Lavoro didattico della prof.ssa Anna Baglivo
Problema_2
Si colloca in cima ad un piano scabro, inclinato di 45° rispetto al piano orizzontale, un blocco di
legno di 2Kg. Tra le superfici a contatto sussiste un coefficiente di attrito statico µs=0,5 ed un
coefficiente di attrito dinamico
µd=0,3.
1) Verificare che il blocco
lasciato libero scende lungo
il piano.
2) Nell’ipotesi che il piano
inclinato sia lungo 76 cm,
determinare il modulo della
velocità con cui il blocco
giunge alla base del piano.
3) Una volta sul piano
orizzontale,
il
blocco
prosegue il suo moto su una
superficie liscia fino a
scontrarsi con una molla,
bloccata in un estremo,
avente costante elastica k=
200N/m . Determinare la
compressione della molla.
Soluzione
1
Una volta lasciato libero il blocco sul piano
inclinato su di esso agisce la forza peso e la
reazione R vincolare del piano. Il piano è
scabro, dunque è in grado di esercitare una
forza d’attrito che tende ad ostacolare il moto.
Il blocco rimane fermo sul piano inclinato se
la componente del peso parallela al piano
d’appoggio ha modulo minore o uguale a quello della forza d’attrito. Si chiede di
verificare che il blocco si muoverà, quindi occorre provare che risulta: P//>R//
Ricordiamo che se il piano è inclinato dell’angolo α rispetto al piano orizzontale
allora la componente del peso del blocco parallela al piano d’appoggio ha modulo
P // = mg ⋅ senα ,
mentre il modulo della componente perpendicolare allo stesso piano è
P ⊥ = mg ⋅ cos α
La forza d’attrito che si esercita tra il blocco ed il piano, finché il blocco rimane
fermo, è il prodotto del coefficiente di attrito statico con la componente del peso che
preme perpendicolarmente sul piano, quindi
Fatt . = µ s ⋅ P ⊥ = µ s ⋅ mg ⋅ cos α
Calcolo dei valori
m 2
P // = mg ⋅ sen 45° = 2 Kg ⋅ 9,81 2 ⋅
≈ 13,87N
s
2
Luigi Lecci:www.matematicaescuola.it 94
Lavoro didattico della prof.ssa Anna Baglivo
Fatt . = µ s ⋅ mg ⋅ cos 45° = 0,5 ⋅ 2 Kg ⋅ 9,81
2
m 2
⋅
≈ 6,94N
s2 2
Poiché Fatt<P// il blocco scivolerà lungo il piano.
Sul blocco, una volta in moto, lungo la direzione del moto agiscono la forza di attrito
dinamico
Fattd . = µ d ⋅ mg ⋅ cos 45°
che si oppone al moto ed ancora la componente della forza peso parallela al piano
inclinato:
P // = mg ⋅ sen 45°
L’intensità della forza risultante nel verso del moto è
P // − Fattd . = mg ⋅ sen 45° − µd ⋅ mg ⋅ cos 45° = (13,87 − 4,16 ) N = 9,71N
Calcolo della velocità con cui il blocco giunge alla base del piano
Possiamo applicare il teorema dell’energia cinetica per determinare la velocità
richiesta. Infatti, il lavoro svolto dalla risultante delle forze che agiscono su un corpo
in moto è uguale alla variazione dell’energia cinetica che il corpo subisce. Ebbene,
visto che il corpo è inizialmente fermo e che la risultante delle forze durante il moto è
costante, parallela al piano del moto e diretta nello stesso verso, conoscendo la
lunghezza l del piano inclinato possiamo scrivere:
1
2( P// − Fatt ) ⋅ l
2 ⋅ 9,71N ⋅ 0,76m
≈
mV f2 = ( P// − Fatt ) ⋅ l ⇒V f =
2
2 Kg
m
m
≈ 2,72
s
3
Poiché il blocco si muove su un piano
orizzontale liscio il suo moto sarà rettilineo
uniforme finché non si scontrerà con la molla
indicata. Arriverà dunque all’impatto con
velocità parallela al piano di scorrimento e con
energia cinetica pari a
1
mV f2 .
2
Durante il processo di compressione della molla l’energia meccanica si trasforma
gradualmente da energia di movimento in energia elastica immagazzinata dalla molla.
Indicata con ∆x la misura della compressione della molla quando il blocco sarà stato
arrestato sussiste l’uguaglianza
1
1
m
mV f2 = k ∆x 2 ⇒ ∆x = V f ⋅
2
2
k
Sostituendo i valori delle grandezze note si ha
∆x = 2,72
m
2 Kg
⋅
≈ 27, 2cm
s
200 Nm −1
Per le valutazioni assegnate agli allievi vedere la relativa scheda
Luigi Lecci:www.matematicaescuola.it 95
Lavoro didattico della prof.ssa Anna Baglivo
Frequenze delle fasce dei voti
8%
4%
8%
20%
16%
[0;4,5]
]4,5;5,5]
]5,5;6,5]
]6,5;7,5]
]7,5;8,5[
[8,5;10]
44%
Luigi Lecci:www.matematicaescuola.it 96
Lavoro didattico della prof.ssa Anna Baglivo
CONCLUSIONI ED AUTOVALUTAZIONE
A conclusione di questo biennio di formazione credo di poter affermare di aver imparato molte
cose a me ancora sconosciute.
La scuola, infatti, mi ha fornito nozioni che non riguardano solo le materie disciplinari, ma
anche materie trasversali, lontane dalla mia formazione universitaria, ma necessarie per formare
la figura di un insegnante educatore, che non deve solo avere conoscenze della disciplina di sua
competenza, ma deve avere anche capacità di riflessione ed autocritica, di comprensione e di
sostegno nei confronti degli alunni.
Anche i laboratori didattici mi sono stati utili per approfondire la conoscenza di alcune
applicazioni di programmi. Senza dubbio, comunque, l’attività più interessante e quella a mio
avviso più formativa è stata il tirocinio diretto a scuola, a stretto contatto con il mondo dei
docenti e degli alunni. Essendo stata una tirocinante 270 h ed avendo avuto un tutor molto
disponibile, ho avuto la possibilità di partecipare attivamente all’attività didattica in tutte le sue
forme ed espressioni. Non essendo ancora un’insegnante, e non essendo più una alunna, mi sono
trovata a cavallo tra questi due mondi, e ciò mi ha dato la possibilità di vedere e studiare le
esigenze dei ragazzi, di ascoltare i discorsi degli insegnanti in sala professori, di confrontare le
mie osservazioni personali sulle classi, che mi erano state assegnate con il mio tutor. Sono certa
dunque che la scuola di specializzazione, e in particolar modo il tirocinio diretto, mi hanno fatto
acquisire quelle conoscenze e competenze che mi permetteranno di affrontare il mondo della
scuola con più professionalità e meno timore.
Luigi Lecci:www.matematicaescuola.it 97
Lavoro didattico della prof.ssa Anna Baglivo
BIBLIOGRAFIA
P.O.F. del liceo ” G. Stampacchia”, Tricase (2005)
Lamberti L., Mereu L., Nanni A., Matematica Uno, Etas (2003)
N. Dodero, P. Baroncini, R. Manfredi, Moduli di Lineamenti di Matematica, Ghisetti e
Corvi Editori (2004)
A. Trifone, M. Bergamini, Le coniche e le trasformazioni nel piano cartesiano, Zanichelli
(2004)
Walter Maraschini, Multi Format- Coniche e loro proprietà, paravia (2004)
G. Zwinner, Itinerari nella matematica, Cedam (1993)
E. Bergamaschini P. Marazzini L. Mazzoni, L’indagine del mondo fisico, Carlo Signorelli
Editore (2004)
James S. Walker, Fisica, Zanichelli (2004)
A. Caforio, A. Ferilli, Nuova Physica 2000,Le Monnier (2000)
Luigi Lecci:www.matematicaescuola.it 98












