ANALISI AI NODI

4. METODI SISTEMATICI PER LA SOLUZIONE DELLE
RETI ELETTRICHE.
4.1 Grafo Planare.
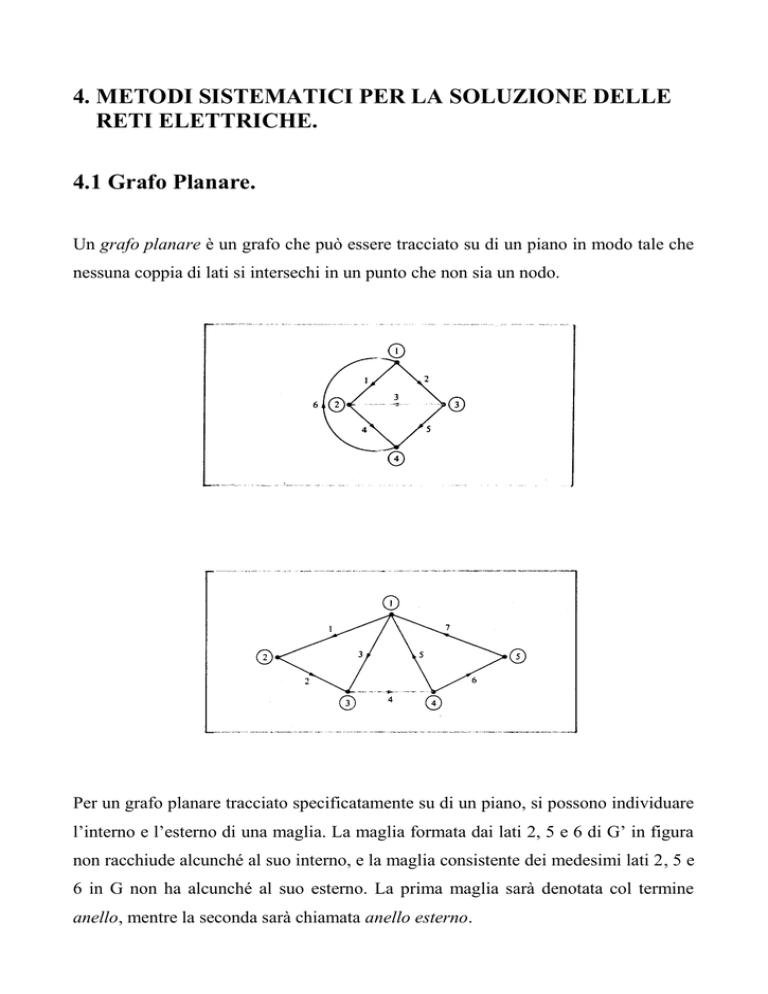
Un grafo planare è un grafo che può essere tracciato su di un piano in modo tale che
nessuna coppia di lati si intersechi in un punto che non sia un nodo.
Per un grafo planare tracciato specificatamente su di un piano, si possono individuare
l’interno e l’esterno di una maglia. La maglia formata dai lati 2, 5 e 6 di G’ in figura
non racchiude alcunché al suo interno, e la maglia consistente dei medesimi lati 2, 5 e
6 in G non ha alcunché al suo esterno. La prima maglia sarà denotata col termine
anello, mentre la seconda sarà chiamata anello esterno.
4.1.1 GRAFO NON ARTICOLATO.
Un grafo non articolato gode della proprietà che ogni qualvolta viene suddiviso
in
due sottografi connessi e non degeneri, i sottografi hanno almeno due nodi in
comune.
4.2 Analisi degli insiemi di taglio.
Tensioni d’albero.
LKC
Qi  0
LKT
v   Q T v albero 
Gli elementi devono essere controllati in tensione
i  f v 
Yq* (D)v albero   igq 
4.3 Analisi ai nodi.
A i  0
LKC
( n 1) 1
v  A T  e
LKT
1
( n 1) ( n 1)1
Tutti gli elementi devono essere controllati in tensione
i  f v
 
Af AT  e 0
 
i  f AT  e

n-1 equazioni non lineari
nelle incognite
e 
Nel caso di reti lineari t. i. distinguiamo
1) analisi in transitorio nel dominio del tempo (non si considera mai in un lato la
presenza contemporanea di un conduttore e un capacitore) allora
i K  A  Dv K ( t )  i gK
ed in generale
i( t)  Y( D)v( t)  i g ( t)
Es:
i K  CDv K  i*gK
Sostituendo nella LKC e LKT si ottiene:

AY( D)v( t )  i*g  0
 
 
AY( D) AT e( t )  i*g ( t )  0
che si scrive
Y*(D)e(t)  ig (t)
iGk(t) somma di tutte le
correnti impresse che
entrano nel nodo K
matrice che esprime gli
operatori “integrodifferenziali”
tra i nodi (simile alla matrice
delle ammettenze di nodo in s)
Le caratteristiche della matrice
di
Y ( D).
Y*(D)
dipendono principalmente dalle proprietà
In assenza di accoppiamenti tra i vari lati i termini di
Y*(D)
possono ottenersi
direttamente in quanto Yii(D) rappresenta la somma delle ammettenze operatoriali
che afferiscono al nodo i e Yij(D) rappresenta la somma delle ammettenze operatoriali
tra il nodo i ed il nodo j.
Nel caso in cui esistano accoppiamenti distinguiamo i casi in cui la matrice
Y ( D)
è ancora simmetrica (es. mutui accoppiamenti di tipo induttivo) dal caso più generale
in cui
Y ( D) perde ogni caratteristica di simmetria (es. generatori pilotati)
2) reti risolte con Laplace
idem
3) reti in regime sinusoidale
idem
4)
Y( D)  Y(s)
Y( D)  Y( j)
reti resistive (matrice diagonale di pure conduttanze)
idem
Y( D)  G
4.4 Analisi delle maglie e degli anelli.
LKT
Bv  0
LKC
i  BT J
Le leggi di lato devono potersi esprimere sotto forma di
v  f i
lati controllati in corrente
Nel caso di reti lineari tempo invarianti si perviene infine alle equazioni
v  Z(D)i  vg 
da cui sostituendo
BZ(D)i  vg   0
BZ(D)BT J  v*g 
ossia
Z*(D)J  v*g 
Esempio generico di lato K
vK  L
di K
 vgK
dt
4.5 Dualità.
Si considera un grafo G, connesso, non articolato e planare, con n t=n+1 nodi, b lati e
quindi
 =b-n
anelli (senza contare l’anello esterno). Un grafo planare
Ĝ
è detto
grafo duale di un grafo G se:
 vi è una corrispondenza biunivoca tra gli anelli di G (incluso l’anello esterno)
ed i nodi di
Ĝ ;
 vi è una corrispondenza biunivoca tra gli anelli di
Ĝ
(incluso l’anello esterno)
ed i nodi di G;
 vi è una corrispondenza biunivoca tra i lati di ciascun grafo in modo che ogni
qualvolta due anelli di un grafo hanno il lato corrispondente in comune, i nodi
corrispondenti dell’altro grafo sono collegati dal lato corrispondente;
Dalla definizione ne segue che
Ĝ
ha b lati,
 +1
nodi, n anelli ed un solo anello
esterno.
Se
Ĝ
è un grafo duale di G, allora G è un grafo duale di
Ĝ .
In altre parole, la
dualità è una relazione simmetrica tra grafi connessi, planari e non articolati.