2013/2014
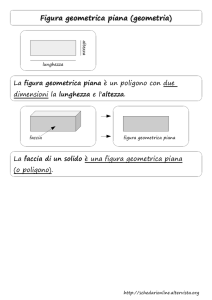
Fondamenti della matematica e della logica
Geometria
27. A ché distanza si trova l’orizzonte, contemplato dal picco di una montagna di 2000m di
altezza? (Supponiamo che la Terra è una sfera di diametro 12.756 km.)
C
28. Voliamo conoscere l’altezza di una torre. Usando un
goniometro e un metro facciamo le misure che si indicano
nella figura, laddove ↵ = 60 , = 45 e d = 5m. Quanto
vale l’altezza?
↵
H
A
d
B
29. Voliamo conoscere l’altezza di un albero che
c’è su una colina. Con un goniometro abbiamo
preso le misure che si indicano nella figura, laddove
↵ = 27 , = 12 , e la distanza da A a B, che è
stata calcolata previamente, è 40m. Quanto vale
l’altezza dell’albero?
30. Calcolare l’area di un appezzamento di terreno triangolare, sapendo che due dei suoi lati
misurano 80m e 130m, rispettivamente, e formano un angolo fra loro di 70 .
31. Tre paesi A, B e C stanno uniti per strade rette. La distanza da A a C è di 6km e quella
da B a C è di 9km. L’angolo che formano le due strade è di 120 . Qual è la distanza da A
a B?
32. In un parallelogramma di perimetro 460cm, la differenza tra lato maggiore e lato minore
è 50cm, mentre l’altezza relativa al lato minore è 28cm. Calcolare:
(i) L’area della figura.
(ii) L’altezza relativa al lato maggiore.
33. In un trapezio isoscele la somma delle basi è 12cm, la differenza delle basi è 8cm, il lato
obliquo è 5cm. Calcolare:
(i) Il perimetro del trapezio.
(ii) L’area del trapezio.
34.
(i) Quanto vale l’angolo interno di un triangolo equilatero?
(ii) Quanto vale l’angolo interno di un quadrato?
(iii) Quanto vale l’angolo interno di un pentagono?
(iv) Quanto vale l’angolo interno di un poligono regolare di n lati?
5
2013/2014
Fondamenti della matematica e della logica
35. Date due quantità no negative a, b, la loro media aritmetica è definita come ma = a+b
,
2
p
e la loro media geometrica come mg = a · b. Dimostra che la media aritmetica e la media
geometrica si possono ottenere graficamente così:
Suggerimento: Dimostra che il segmento BE nella
D E
figura soddisfa:
ma
a
BE
=
.
BE
b
mg
(Per questa ragione, alla media geometrica si la
chiama anche medio proporzionale.)
Ragionando sulla figura, risponde giustificatamente le seguenti domande:
A
a
M
B
b
C
(i) Per a ché valori di a e b media aritmetica è 0?
(ii) Per a ché valori di a e b la media geometrica è 0?
(iii) Può essere la media geometrica più grande che la media aritmetica?
(iv) Può essere la media geometrica uguale a la media aritmetica? Quando?
36. Il perimetro di un poligono è la somma delle misure
dei suoi lati. Dimostra che l’area di un poligono regolare è
A = p·a
, laddove p è il perimetro del poligono e a è la sua
2
apotema.
a
37. Il perimetro di una circonferenza di raggio r viene dato per la formula p = 2⇡r, laddove
⇡ è una costante che vale circa 3, 1416. Infatti, una definizione molto comune di ⇡ è “il
rapporto tra la lunghezza di una circonferenza e il suo diametro”. Data una circonferenza
di raggio r, possiamo inscrivere successivi poligoni regolari, come si mostra nella seguente
figura:
a
r
a
r
a
r
...
Ragionando sempre su questa figura, a ché valore si approssima l’apotema di un poligono
regolare quando il numero di lati è molto grande? A ché valore si approssima il perimetro
del poligono regolare quando il numero di lati è molto grande? E a ché valore si approssima
l’area del poligono regolare quando il numero di lati è molto grande? Puoi dedurre di questo
una formula per calcolare l’area di un cerchio di raggio r?
6