APPELLO STATICA 16 FEBBRAIO 2017
a) Baricentro (vincolo)
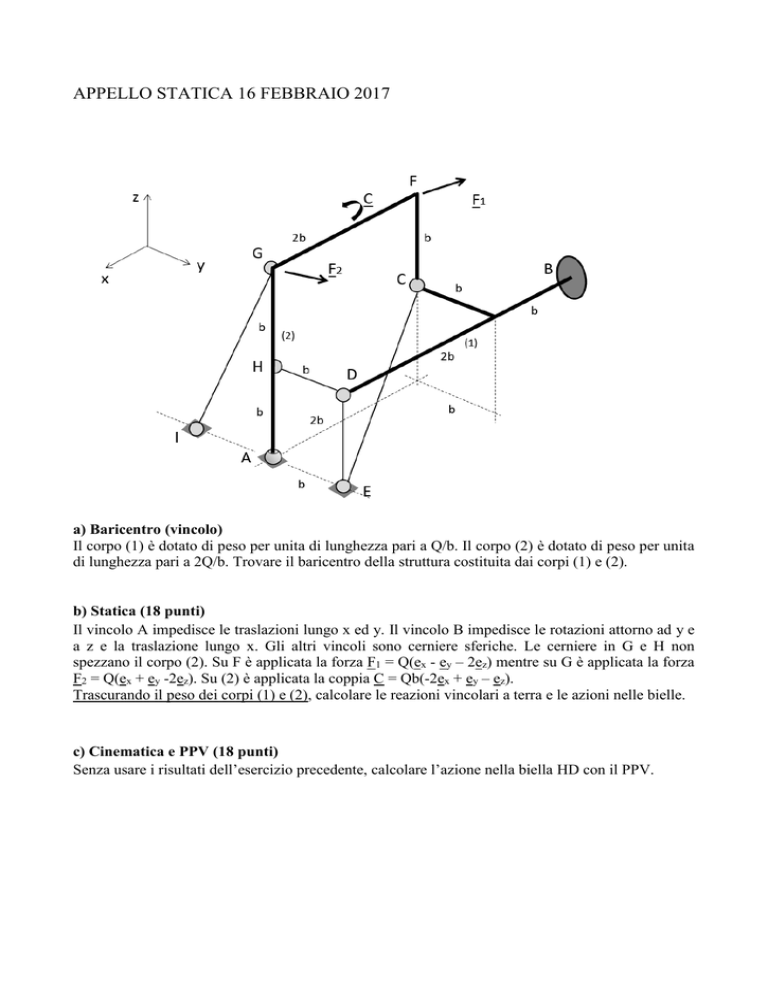
Il corpo (1) è dotato di peso per unita di lunghezza pari a Q/b. Il corpo (2) è dotato di peso per unita
di lunghezza pari a 2Q/b. Trovare il baricentro della struttura costituita dai corpi (1) e (2).
b) Statica (18 punti)
Il vincolo A impedisce le traslazioni lungo x ed y. Il vincolo B impedisce le rotazioni attorno ad y e
a z e la traslazione lungo x. Gli altri vincoli sono cerniere sferiche. Le cerniere in G e H non
spezzano il corpo (2). Su F è applicata la forza F1 = Q(ex - ey – 2ez) mentre su G è applicata la forza
F2 = Q(ex + ey -2ez). Su (2) è applicata la coppia C = Qb(-2ex + ey – ez).
Trascurando il peso dei corpi (1) e (2), calcolare le reazioni vincolari a terra e le azioni nelle bielle.
c) Cinematica e PPV (18 punti)
Senza usare i risultati dell’esercizio precedente, calcolare l’azione nella biella HD con il PPV.
TRACCIA DI SOLUZIONE
1
Baricentro
L’origine del sistema di riferimento è posizionato in A
CORPO
PESO
xG
yG
zG
Asta AG
4Q
0
0
b
Asta GF
4Q
−b
0
2b
Asta FC
2Q
−2b
0
3
b
2
Asta BD
3Q
3
− b
2
b
b
Asta CK
Q
−2b
b
2
b
Il peso totale della struttura è:
PT OT = 14Q
Mentre le coordinate del baricentro risultano:
29
b
xG = − b
yG =
28
4
2
zG =
19
b
14
Statica
Forze esterne:
F 1 = Q(ex − ey − 2ez ) in F
F 2 = Q(ex + ey − 2ez ) in G
C = Qb(−2ex + ey − ez ) su (2)
Forze incognite:
FA
FB
CB
FE
= (FAx ex + FAy ey ) in A
= FBx ex in B
= (CBy ey + CBz ez ) su B
= (FEx ex + FEy ey + FEz ez ) in E
1
T DE = α(−ez )
T GI = β(−ey − 2ez )
T CE = γ(2ex + ey − ez )
T HD = δey
in D
in G
in C
in H
N.B. Le forze nelle bielle saranno di trazione se i parametri incogniti saranno positivi, di compressione altrimenti.
Considero il corpo (1)
Mx (C) = −αb = 0 ⇒ α = 0
My (C) = CBy + 2αb = 0 ⇒ CBy = 0
Considero il sistema globale
Mx (E) = 2βb + 2βb − 2Qb + 2Qb + 2Qb + 2Qb − 2Qb = 0
My (E) = FBx b + Qb + 2Qb + 2Qb − 4Qb = 0 ⇒
Rz = FEz − 2β − 2Q − 2Q = 0 ⇒ FEz = 3Q
⇒
FBx = −Q
1
β=− Q
2
Considero la cerniera E
Rz = FEz + α + γ = 0 ⇒ γ = −3Q
Rx = FEx + −2γ = 0 ⇒ FEx = −6Q
Ry = FEy − γ = 0 ⇒ FEy = −3Q
Considero il corpo (2)
5
FAy = Q
2
My (C) = −FAx b + 4βb + Qb + Qb + 4Qb + Qb = 0 ⇒ FAx = 5Q
7
Mz (C) = 2δb + 2FAy b − 2βb − Qb + 2Qb = 0 ⇒ δ = − Q
2
Mx (C) = FAy b + βb − 2Qb + Qb + Qb = 0
⇒
Considero il corpo (1)
Mz (C) = CBz − FBx b − 2δb = 0
⇒
2
CBz = −8Qb
3
Cinematica e PPV
Per calcolare l’azione esercitata dalla biella HD occorre studiare gli atti di moto
della struttura senza la biella stessa.
Scegliamo B come polo per il corpo (1) e A per il corpo (2).
U (1) (M ) = UBy ey + UBz ez + ωx(1) ex ∧ BM
U (2) (M ) = UAz ez + ω (2) ∧ AM
Biella DE
U (1) (D) · ez = 0
⇒
UBz = 0
Biella GI
U (2) (G) · (ey + 2ez ) = 0
UAz = ωx(2) b
⇒
Biella CE
U (1) (C) · (2ex + ey − ez ) = 0
⇒
UBy = −ωx(1) b
Cerniera in C
U
(1)
(C) = U
(2)
(C)
⇒
(2)
ωy
(2)
ωx
(2)
ωz
=0
= −ωx(1) = −ω
= ωx(1) = ω
Gli atti di moto in funzione di ω risultano
U (1) (M ) = −ωbey + ωex ∧ BM
U (2) (M ) = −ωbez + ω(−ex + ez ) ∧ AM
PPV
P = T HD · (U (2) (H) − U (1) (D)) + C · ω (2) + F 1 · U (2) (F ) + F 2 · U (2) (G) = 0
⇒ P = 2δωb + Qωb + 2Qωb + 4Qωb = 0
3
⇒
7
δ=− Q
2