ESERCITAZIONE 8
• DESCRIVERE LE PROPRIETÀ DEI MAGNETI PERMANENTI.
• PRESENTARE I TIPI DI MATERIALI PIÙ SIGNIFICATIVI.
• FORNIRE I CRITERI GENERALI PER IL LORO USO.
MAGNETI PERMANENTI
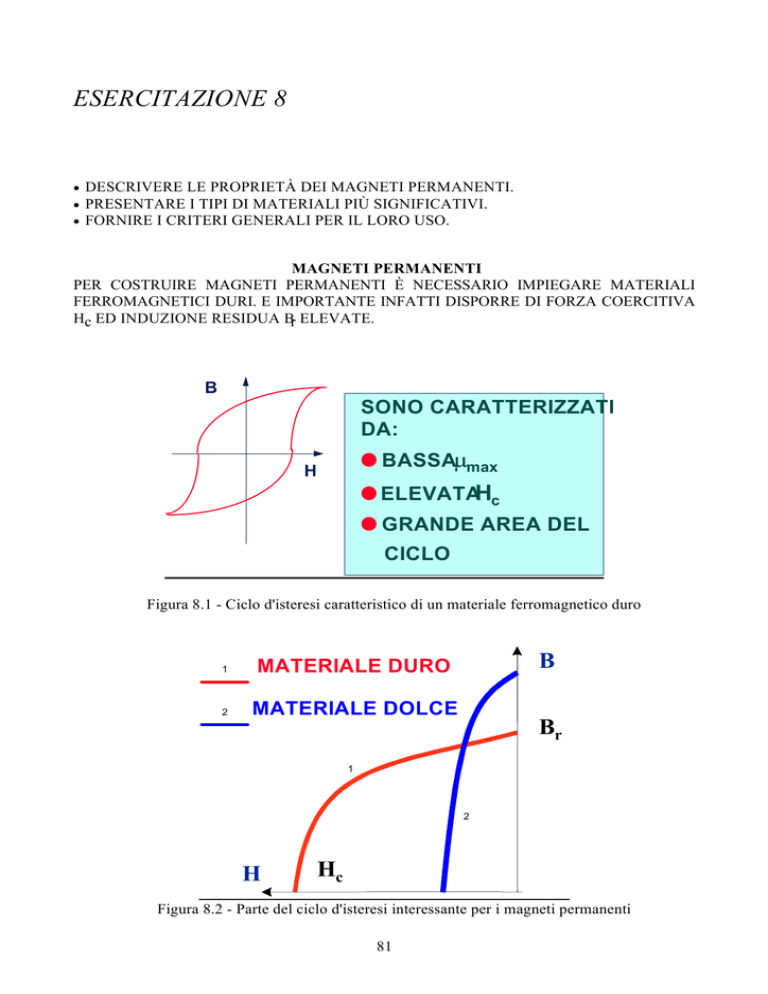
PER COSTRUIRE MAGNETI PERMANENTI È NECESSARIO IMPIEGARE MATERIALI
FERROMAGNETICI DURI. E IMPORTANTE INFATTI DISPORRE DI FORZA COERCITIVA
Hc ED INDUZIONE RESIDUA Br ELEVATE.
B
SONO CARATTERIZZATI
DA:
BASSAµmax
H
ELEVATAHc
GRANDE AREA DEL
CICLO
Figura 8.1 - Ciclo d'isteresi caratteristico di un materiale ferromagnetico duro
1
MATERIALE DURO
2
MATERIALE DOLCE
B
Br
1
2
H
Hc
Figura 8.2 - Parte del ciclo d'isteresi interessante per i magneti permanenti
81
EQUAZIONI GENERALI DEI MAGNETI PERMANENTI
Figura 8.3 - Circuito magnetico di magnete permanente senza traferro
IN UN MAGNETE PERMANENTE SI HA:
∫ Hxdl = 0
E QUINDI
H=0
B=0
PRATICHIAMO ADESSO UN TRAFERO DI AMPIEZZA0l. SI HA ALLORA:
Hf lf = - H0 l0
l0
lf
Figura 8.4 - Circuito magnetico di magnete permanente con traferro
NEL FERRO SI HA:
PERCIÒ NELL’ARIA:
Bf ≠ 0
B0 ≠ 0
82
RICORDIAMO CHE SI HA:
B0 = a Bf
SI DETERMINANO H0 ED Hf :
H0 = B0/m0
DA CUI
a>1
Hf = - H0 (l0/lf)
Hf = −
α l0
Bf
µ 0 lf
L’ULTIMA ESPRESSIONE DI Hf IN FUNZIONE DI Bf È L’EQUAZIONE DI UNA RETTA
CON COEFFICIENTE ANGOLARE PARI A:
- (al0) / (m0lf)
SI PUÒ QUINDI DETERMINARE SULLA CARATTERISTICA DEL MATERIALE SCELTO IL
PUNTO DI LAVORO CARATTERIZZATO DAI VALORI (H
f, Bf)
1
MATERIALE DURO
2
MATERIALE DOLCE
B
Hf = - (α
α l0 Bf) / (µ
µ0 lf)
Bf
1
H
2
Hf
Figura 8.5 - Determinazione del punto di lavoro di un magnete permanente
OSSERVIAMO CHE SI HANNO LE SEGUENTI SITUAZIONI:
PER l0 = 0 Bf = Br
PER l0 ≠ 0 Bf < Br
Hf = 0
Hf ≠ 0
CONSIDERAZIONI ENERGETICHE
L’ENERGIA MAGNETICA AL TRAFERRO VALE:
W = 1/2 m0 H02 V0 = 1/2 m0 (B0/m0) Hf (lf/l0) l0 S0 = 1/2 Hf lf a Bf S0
DOVE
V0 = VOLUME DEL TRAFERRO
83
S0 = SEZIONE DEL TRAFERRO
SE SI HA: S0 = Sf
ED È:
Vf = VOLUME DEL FERRO
W = 1/2 a Vf Bf Hf
A PARITÀ DI ENERGIA SI CHE IL VOLUME DEL FERRO È MINIMO QUANDO IL
PRODOTTO Bf Hf È MASSIMO. SI PUÒ Così DETERMINARE IL PUNTO DI LAVORO
PIÙ CONVENIENTE
B
Bf
H
BH
Hc
(BH)MAX
Figura 8.6 - Punto di lavoro di massima energia di un magnete permanente
SE SI HA UNA VARIAZIONE DEL TRAFERRO O SMAGNETIZZAZIONE DEL MAGNETE
PERMANENTE CHE PORTI A VARIAZIONI DI Hf E DI Bf IL MATERIALE DESCRIVE DEI
CICLI PARZIALI CHE SONO SPESSO ASSIMILATI A RETTE, CHIAMATE RETTE DI
RITORNO.
B
Br
Br1
Hc
H
Figura 8.7 - Retta di ritorno e ciclo di isteresi locale
MATERIALI PER MAGNETI PERMANENTI
I MATERIALI PER MAGNETI PERMANENTI POSSONO ESSERE OTTENUTI CON LE
SEGUENTI TECNOLOGIE:
• PER COLATA
84
• PER SINTERIZZAZIONE
• MATERIALI OTTENUTI DA POLVERI FINISSIME
MATERIALI OTTENUTI PER COLATA
PER AVERE Hc ELEVATO BISOGNA OSTACOLARE IL LIBERO MOVIMENTO DEI
DOMINI AD ES. CON TRATTAMENTO DI TEMPRA. SONO DISPONIBILI I SEGUENTI
MATERIALI:
• ACCIAI MARTENSITICI.
• LEGHE ALNI E ALNICO.
• GLI ACCIAI MARTENSITICI SONO STATI I PRIMI MATERIALI DISPONIBILI.
• LE LEGHE ALNI SONO LEGHE DI Fe CON Ni ED Al.
• LE LEGHE ALNICO SONO LEGHE DI Fe CON Ni, Al (O Ti) E Co.
SIA LE LEGHE ALNI CHE LE LEGHE ALNICO POSSONO ESSERE TENSIONATE
INTERNAMENTE CON RAFFREDDAMENTI RAPIDI.
Tabella 8.1 - Caratteristica di materiali per magneti permanenti ottenuti per colata
MATERIALE
ACCIAIO 1% C
ACCIAIO AL W
ACCIAIO AL Co
ALNI
ALNICO 2
Hc
(As/m)
4.000
12.000
20.000
42.000
44.000
Br (BH)M
(T)
AX
0,90
2.000
0,95
5.000
0,95
7.500
0,58 10.000
0,70 16.000
MATERIALI OTTENUTI PER SINTERIZZAZIONE
SONO ANCORA I MATERIALI TIPO ALNI ED ALNICO CHE, PER DIMINUIRE I COSTI,
POSSONO ESSERE OTTENUTI CON PROCESSI DI SINTERIZZAZIONE PARTENDO DAL
MATERIALE IN POLVERE. SI HA UN LEGGERO DECADIMENTO DELLE
CARATTERISTICHE. SI USANO ANCHE CON OTTIMI RISULTATI LEGHE
SINTERIZZATE DI FERRO CON ALTRI ELEMENTI E DI COBALTO CON TERRE RARE:
l LEGA AL SAMARIO - COBALTO (Sm2Co17)
l LEGA DI FERRO, NEODIMIO E BORO
SI PUÒ OTTENERE UN MATERIALE ANISOTROPO PRESSANDO LE POLVERI SOTTO
L’AZIONE DI UN CAMPO MAGNETICO. APPARTENGONO A QUESTI TIPI L’ALNICO 5
CHE PUÒ ESSERE OTTENUTO CON MAGNETIZZAZIONE DIREZIONALE E CON
CRISTALLI ORIENTATI.
Tabella 8.2 - Caratteristica di materiali sinterizzati
MATERIALE
Hc (As/m)
Bs (T)
ALNI
ALNICO 2
ALNICO 5 M dir
ALNICO 5 xx or
Sm2 Co17
Nd Fe B
40.000
42.000
48.000
65.000
750.000
840.000
0,58
0,70
1,2
1,35
1,06
1.12
85
(BH)MAX
(J/m3)
8.800
13.500
36.000
68.000
260.000
300.000
MATERIALI CERAMICI OTTENUTI DA POLVERI FINISSIME
SI PUÒ RIDURRE UN MATERIALE PER MAGNETI PERMANENTI IN GRANULI DELLA
DIMENSIONE DI UN DOMINIO. SI HA MAGNETIZZAZIONE SOLO PER SPOSTAMENTO
DELLE PARETI.
CITIAMO COME ESEMPIO LA FERRITE DI BARIO CHE PRESENTA LE SEGUENTI
CARATTERISTICHE:
Hc = 120.000 As/m
Bs = 0,20 T
(HB)MAX = 6.000
TUTTI I MATERIALI USATI PER PRODURRE MAGNETI PERMANENTI SONO DURI E
MOLTO FRAGILI. NON POSSONO QUINDI ESSERE SOTTOPOSTI A LAVORAZIONI PER
ASPORTAZIONE DI TRUCIOLO.
CALCOLO DI CIRCUITI MAGNETICI CON MAGNETI PERMANENTI
Si possono individuare due tipologie di problemi:
•
•
progetto del magnete permanente affinché venga prodotto, nel circuito magnetico in cui è
inserito, un certo flusso o induzione;
determinazione del flusso e dell'induzione all'interno di un circuito magnetico in cui è inserito un
magnete permanente di cui sono note tutte le caratteristiche fisiche e geometriche.
Analizziamo singolarmente i due problemi dando una traccia per la loro soluzione.
Progetto di un magnete permanente
Vengono forniti tutti i dati geometrici relativi ai rami del circuito magnetico (lunghezze e sezioni) e
le caratteristiche dei materiali (curve di magnetizzazione). Si vuole dimensionare un magnete
permanente, di cui è nota la caratteristica di smagnetizzazione B(H), affinché venga prodotto un
certo flusso o una certa induzione in uno dei tronchi del circuito magnetico.
Ad esempio, dato il circuito magnetico rappresentato in fig. 8.8, si vuole determinare la sezione a la
lunghezza del magnete permanente, affinché nel traferro venga raggiunta una induzione
Bt.
Le dimensioni del circuito magnetico sono rispettivamente:
lf
lt
Sf
St
lunghezza del tronco in ferro;
lunghezza del traferro;
sezione del tronco in ferro;
sezione del traferro che possiamo ipotizzare uguale Sat = S f α dove α risulta, per piccoli
traferri, pari circa a 1,05-1,10.
86
lt
lf
Magnete
Tronco in ferro
Figura 8.8 - Circuito magnetico con magnete permanente
Dal valore di induzione voluta al traferro è possibile determinare il valore di induzione nel tronco in
ferro attraverso la relazione:
Bf =
Bt St
= Bt α
Sf
Quindi dai valori di induzione è semplice ricavare i corrispondenti valori di campo magnetico H.
In particolare, nel traferro si ha:
Bt
µ0
mentre per il tronco in ferro occorre leggere sulla caratteristica di magnetizzazione il corrispondente
valore di campo magneticoHf.
La forza magnetomotrice (fmm) che deve fornire il magnete risulta perciò:
Ht =
mm
= Ht lt + H f l f
Scelto un punto sulla caratteristica di smagnetizzazione, ossia una coppia di valori Bm - Hm, è
possibile dimensionare il magnete. Infatti, la sezione è data dalla relazione:
Bf S f
Sm =
Bm
mentre la lunghezza è data dalla formula:
lm =
mm
Hm
Occorre osservare che scegliendo un punto diverso sulla caratteristica si smagnetizzazione si
ottengono valori diversi di sezione e lunghezza del magnete. In particolare, il punto più conveniente
è quello a cui corrisponde il minimo volume del magnete (minor ingombro e minor costo). Tale
punto si ottiene ricavando dalla caratteristica di smagnetizzazione la curva dei prodotti Bm Hm ed
87
andando a scegliere il punto corrispondente al massimo di tale curva il quale coincide con il punto di
massima energia magnetica. Se si indicano con BmM HmM i valori di induzione e campo
corrispondenti a tale punto si ottengono i valori di sezione e lunghezza che danno origine al minimo
ingombro:
Smmin =
lmmin =
Bf S f
BM
mm
HM
Calcolo del flusso o dell'induzione all'interno di un circuito magnetico
Vengono forniti tutti i dati geometrici relativi ai rami del circuito magnetico e del magnete
permanente (lunghezze e sezioni) e le caratteristiche dei materiali (curve di magnetizzazione per i
materiali magnetici e di smagnetizzazione per il magnete permanente). Si vuole determinare il flusso
o il valore dell'induzione in uno dei tronchi del circuito magnetico.
Facendo sempre riferimento alla fig. 8.8, sono perciò noti:
lf
lunghezza del tronco in ferro;
lt
lunghezza del traferro;
lm
lunghezza del magnete permanente;
Sf
sezione del tronco in ferro;
St
sezione del traferro;
Sm
sezione del magnete.
Questo secondo problema, apparentemente più semplice del precedente, risulta invece più complesso
e richiede una soluzione di tipo grafico. La soluzione al problema viene ottenuta andando a
determinare l'intersezione tra la caratteristica fmm-flusso del circuito magnetico (che funge da carico
magnetico) con quella del magnete permanente (il quale funge da generatore magnetico).
L'intersezione delle due curve stabilisce il punto di funzionamento magnetico nonché il valore del
flusso magnetico.
Il tracciamento della curva relativa al magnete permanente viene ottenuta fissando una serie di valori
di induzione Bm sulla caratteristica di smagnetizzazione e nell'andare a leggere i corrispondenti valori
di campo magneticoHm.
Vengono quindi calcolati i corrispondenti valori del flusso e della fmm attraverso le relazioni:
φ = Bm Sm
= Hmlm
In pratica occorre riempire una tabella simile a quella di seguito riportata:
m
Induzione Bm [T]
Bm1
Campo magneticoHm [A/m]
Bm2
Hm (Bm2 )
..
..
H m (Bmn )
..
..
Bmn
Hm (Bm1 )
Flusso φ [Wb]
φ1 = Bm1Sm
φ 2 = Bm2 Sm
..
..
φ n = Bmn Sm
88
Fmm
m
[A]
Fm2
( )
= H (B )l
F mn
..
..
= H m (Bmn )l m
Fm1 = Hm Bm1 lm
m
m2
m
Passiamo ora a determinare la caratteristica del circuito magnetico costituito dal tratto in ferro e dal
traferro. Si fissa una serie di valori di induzione nel ferro B f e sulla caratteristica magnetica del
materiale vengono letti i valori del campo magnetico corrispondenti. L'induzione al traferro ed il
corrispondente campo magnetico vengono determinati utilizzando le già note relazioni:
Bt =
Bf S f
Ht =
Bt
µ0
St
=
Bf
α
Infine la caduta di fmm totale su ferro e traferro risulta data dalla formula:
tot
= H f l f + Ht lt
Anche per il circuito magnetico occorre quindi compilare una tabella come quella sotto riportata:
Induzione nel Campo mag. Induzione nel Campo mag. nel Flusso φ
Fmm tot [A]
ferro Bf [T]
nel ferro Hf traferro Bt [T]
traferro Ht
[Wb]
[A/m]
[A/m]
Bf 1
φ1 = Bm1Sm F = H B l + H l
B
B
f1
H f Bf 1
Ht 1 = t1
tot 1
f
f1 f
t1 t
Bt 1 =
µ0
α
( )
Bf 2
..
..
B fn
( )
H f Bf 2
..
..
( )
Bt 2 =
Bf 2
α
Ht 2 =
..
..
( )
Btn =
H f B fn
Bt 2
µ0
..
..
B fn
α
Htn =
Btn
µ0
( )
φ 2 = Bm2 Sm F = H B l + H l
tot 2
f
f2 f
t2 t
..
..
..
..
φ n = Bmn Sm F = H B l + H l
totn
f
fn f
tn t
( )
Dai dati riportati nelle tabelle vengono tracciate le due caratteristiche di fmm in funzione del flusso
sia per il circuito magnetico che per il magnete permanente. L'intersezione tra le due caratteristiche
fornisce il valore del flussoφ* cercato (fig. 8.9).
[A]
m
tot
φ∗
φ [Wb]
Figura 8.9 - Caratteristica fmm - flusso del circuito magnetico e del magnete permanente.
89