Università degli Studi di Napoli
“Parthenope”
Facoltà di Scienze Motorie
a.a. 2010/2011
STATISTICA
Docente: Paolo Mazzocchi
[email protected]
Programma
1) Tabelle: distribuzioni di frequenze; classi di valori; tabelle a doppia
entrata.
2) Grafici: istogramma; rappresentazione grafica delle frequenze
cumulate; diagramma circolare; grafico a dispersione; alcune
applicazioni del grafico a dispersione.
3) Valori medi: moda; mediana; quartili, decili e percentili; media
aritmetica.
4) Dispersione: campo di variazione; devianza, varianza e scarto
quadratico medio; coefficiente di variazione.
5) Misure di associazione: frequenze congiunte; distribuzioni marginali;
distribuzioni condizionate; media e varianza condizionata; modello di
regressione lineare; stima dei parametri; codevianza e covarianza;
coefficiente di correlazione.
6) Campionamento: indagine censuaria e indagine campionaria;
campionamento probabilistico; campionamento casuale semplice;
campionamento stratificato; campionamento a grappoli e a stadi
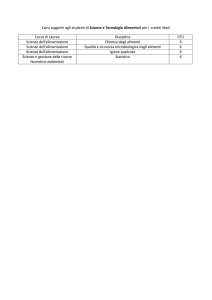
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
Testi consigliati:
“La Statistica”, M.F. Fuller, D.A. Lury, A. Calvelli,
C. Quintano, Liquori Editore, 1982. (Cap. 1; Cap.
2; Cap. 3; Cap. 5 fino a par. 5.27; Cap. 7 fino a
par. 7.59; Cap. 8 da par. 8.1 a 8.5)
Dispense ed esercizi scaricabili dal sito:
• http://www.statmat.uniparthenope.it/
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
MODALITA’ D’ESAME
L’esame si articola in una prova scritta ed in una prova orale.
Ad ogni studente verrà sottoposta una prova costituita da 4 quesiti,
in dettaglio:
• un quesito di tipo I che verte sui seguenti argomenti: media,
moda, mediana (o quartili) e istogramma (o grafico a barre)
• un quesito di tipo II che verte su: media condizionata o varianza
condizionata
• un quesito di tipo III che verte su uno dei seguenti argomenti:
regressione, oppure correlazione e grafico a dispersione oppure
coefficiente di Spearman.
• un quesito di tipo IV che verte sul campionamento
Per la prova scritta si consiglia vivamente di esercitarsi sugli esercizi
svolti a lezione, scaricabili dal sito web sopramenzionato.
Il tempo massimo per lo svolgimento della prova scritta è di 50
minuti.
Si invitano gli studenti a presentarsi dotati di fogli a quadretti e
di calcolatrice.
La prova orale consiste nella discussione della prova scritta ed in un
eventuale accertamento della conoscenza della materia.
Statistica 3 CFU – Sc. Motorie Docente: Paolo Mazzocchi
Carattere statistico, unità
statistiche e modalità
Caratteri statistici
Nome
Unità
Rossi M.
Statistiche Bianchi G.
Nicoletti C.
Marcelli F.
Petrone A.
Età
Sesso
32
39
46
28
51
M
F
M
M
F
Titolo di Attività
studio
Laurea
Occupato
Laurea
Occupato
Diploma Disoccupato
Diploma Studente
Diploma Casalinga
Peso
(kg)
72
55
79
63
64
Punteggio
esercizi
65
55
53
78
21
Modalità del carattere statistico
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
Un CARATTERE può assumere modalità differenti in
corrispondenza delle diverse unità statistiche del COLLETTIVO.
Le modalità del carattere devono essere:
1.
Esaustive: includere tutti
manifestarsi del carattere.
i
2.
Non sovrapposte: ad ogni unità deve essere
associabile una sola modalità.
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
possibili
modi
di
I caratteri statistici si possono
distinguere in:
Variabili:
se le modalità del carattere
statistico sono di tipo quantitativo, cioè
espressi da numeri.
Esempio: Peso.
Mutabili: se le modalità del carattere statistico
sono di tipo qualitativo, cioè non espressi da
numeri
Esempio: Titolo di studio
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
Un carattere QUALITATIVO viene
distinto in:
CARATTERE ORDINATO (o con scala ordinale)
se date due sue modalità è possibile dare un ordine, specificando che
una precede l’altra. A loro volta sono distinguibili in
CARATTERI ORDINATI RETTILINEI – che possiedono cioè una
modalità iniziale ed una finale come ad esempio il TITOLO DI
STUDIO [modalità: senza titolo, licenza elementare, licenza media,
diploma, Laurea, Dottorato]
CARATTERI ORDINATI CICLICI – che hanno le modalità legate da un
ordine naturale di successione ma non hanno vere e proprie
modalità iniziali e finali le quali possono essere fissate solo in modo
convenzionale;
CARATTERE SCONNESSO (o con scala nominale)
se date due modalità è possibile solo affermare se queste sono uguali o
diverse, come ad esempio il SESSO o ATTIVITA’.
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
I caratteri QUANTITATIVI vengono
distinti in CONTINUI e DISCRETI
In un carattere quantitativo DISCRETO l’insieme delle modalità assumibili
può essere messo in corrispondenza biunivoca con un sottoinsieme
dei numeri interi (quindi le modalità assumibile da un carattere
discreto sono in NUMERO FINITO o al più un infinito numerabile)
Esempi di caratteri discreti sono: il numero di figli, il voto ad un esame
In un carattere quantitativo CONTINUO l’insieme delle modalità
assumibili può essere messo in corrispondenza biunivoca con un
sottoinsieme dei numeri reali.
Esempi di caratteri quantitativi continui sono il peso e l’altezza
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
Carattere statistico, unità
statistiche e modalità
MUTABILI
Nome
Età
Sesso
Rossi M.
Bianchi G.
Nicoletti C.
Marcelli F.
Petrone A.
32
39
46
28
51
M
F
M
M
F
Titolo di Attività
studio
Laurea
Occupato
Laurea
Occupato
Diploma Disoccupato
Diploma Studente
Diploma Casalinga
VARIABILI
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
Peso
(kg)
72
55
79
63
64
Punteggio
esercizi
65
55
53
78
21
Distribuzioni unitarie
Le distribuzioni statistiche descrivono il modo in
cui
uno
o
più
caratteri
si
manifestano
(distribuiscono) in un dato collettivo.
L’elenco delle modalità osservate, unità per
unità si chiama distribuzione unitaria.
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
Esempio: distribuzione unitaria semplice per
il carattere statistico «genere»
Soggetto
intervistato
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Genere
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
F
F
M
F
M
M
M
F
F
M
F
F
F
F
M
M
F
M
F
F
Distribuzione di frequenze
Distribuzione di frequenze assolute
Associa alle modalità che può assumere un
carattere X le corrispondenti frequenze assolute
Frequenza assoluta ni
Numero di volte che la modalità di un carattere
viene osservata nel collettivo (N)
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
Dalla distrib. unitaria alla distrib. di frequenze
Soggetto
intervistato
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Genere
F
F
M
F
M
M
M
F
F
M
F
F
F
F
M
M
F
M
F
F
Sesso
M
Frequenza
assoluta ni
8
F
12
Totale
20
Frequenza assoluta ni
Numero di volte che la modalità di un carattere
viene osservata nel collettivo (N)
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
Dalla distrib. unitaria alla distrib. di frequenze
semplici
Leggendo per riga: Modalità dei
caratteri osservati in corrispondenza di
ciascuna unità del collettivo in esame
Leggendo per colonna:
distribuzione unitaria
semplice di un carattere
Distribuzioni di frequenze semplici
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
Le Tabelle statistiche
La classificazione delle unità statistiche rilevate, secondo le
modalità di uno o più caratteri, dà luogo alle tabelle statistiche,
che possono essere:
semplici se si considera un solo carattere;
multiple se si considerano due o più caratteri per ogni unità
X
x1
Freq.
ass.
n1
x2
n2
….
….
xJ
nj
x1 , x2 ,.....x j
X
n , n ,.....n
j
1 2
Frequenze relative e percentuali
La frequenza relativa fi è la frazione di collettivo che presenta la
modalità j-esima
La frequenza percentuale pi è uguale alla frequenza relativa [fi]
moltiplicata per 100.
Genere
Freq.
assoluta
Freq.
relativa
Freq.
percentuale
M
8
0,4
40%
F
12
0,6
60%
Totale
20
1
100%
Freq. percentuale
Freq. relativa
pi
n
fi i
N
ni
100 f i 100
N
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
Frequenza cumulata
La frequenza cumulata di una classe è data dalla somma
della frequenza della classe con quella delle classi
precedenti.
Frequenza assoluta cumulata:
j
N j ni
i1
Frequenza relativa cumulata:
j
Fj fi
i 1
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
Frequenze
pi
ni
100 f i 100
N
X
Freq.
ass.
Freq.
rel.
Freq.
Perc.
Freq.
ass.
cum.
x1
n1
f1
p1
N1 =n1
x2
n2
f2
p2
N2
F2 =f1+f2
=n1+n2
….
…
….
…
xJ
nj
fj
pj
Nj
Freq.
rel.
cum.
Freq.
perc.
cum.
F1=f1
P1=p1
P2=p1
+p2
Fj
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
Esempi
Titolo di studio
frequenza assoluta
frequenza assoluta
cumulata
Lic. Media
Diploma
Laurea
Totale
3
6
11
20
3
9
20
-
Titolo di studio
frequenza relativa
Frequenza percentuale
Lic. Media
Diploma
Laurea
Totale
0,15
0,3
0,55
1
15%
30%
55%
100%
Titolo di studio
Frequenza relativa
cumulata
frequenza percentuale
cumulata
Lic. Media
Diploma
Laurea
Totale
0,15
0,45
1
-
15%
45%
100%
-
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
Pj
Distribuzioni con classi di valori
Distribuzione unitaria delle Ore di allenamento
mensile di un collettivo di clienti di una palestra
48
42
53
51
36
45
51
62
49
50
44
56
53
59
55
41
39
58
57
46
45
38
41
57
64
46
53
55
62
47
58
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
Le distribuzioni di frequenza aiutano a “leggere”
l’informazione statistica…
Distribuzione di frequenza con classi di valori dei dati
relativi alle ore di allenamento mensile di un collettivo
di clienti di una palestra
Ore di allenam.
Spoglio
Frequenza
da 35 a 39
111
3
da 40 a 44
1111
4
da 45 a 49
1111111
7
da 50 a 54
111111
6
da 55 a 59
11111111
8
da 60 a 64
111
3
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
Scelta delle classi di valori
Nel raggruppare i dati, si posso scegliere classi di valori di
ampiezza uguale o disuguale.
Le classi di valori in cui non si definiscono i limiti inferiore e
superiore vengono dette aperte (ma un’intervallo aperto è
fonte di poca chiarezza!!!)
Ore di allenamento
xx
i
Intervallo
chiuso
(l’estremo è
compreso nella
classe)
Intervallo
aperto
(l’estremo non
è compreso
nella classe)
Numero
[0-50[
14
[50 -64]
17
Totale
31
xi
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
xi+1
Esempio di
intervallo
«chiuso a
sinistra» ed
«aperto a
destra»
Rappresentazioni grafiche:
Vantaggi
Visualizzazione immediata
Confronto
Potenzialità investigative
Evidenza divulgativa
Aspetti
Semplicità (efficacia)
Chiarezza
Accuratezza
Aspetto (armonia)
Struttura
Caratteristiche
Titolo
Carattere
Unità di misura
Fonte
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
Alcune rappresentazioni grafiche:
Ortogrammi (Diagrammi a barre o a nastri)
Diagrammi circolari
pj
100
gj
360
da cui g j
p j 360
100
Cartogrammi, cartodiagrammi etc
Diagramma cartesiano
Istogramma (con classi di ampiezza uguale e
differente)
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
ALCUNE RAPPRESENTAZIONI GRAFICHE DI
INFORMAZIONI STATISTICHE
Diagramma a barre (o a nastri)
Per la costruzione di un DIAGRAMMA A BARRE si disegna, per
ogni modalità del carattere statistico, un segmento (barra) di
lunghezza pari alla frequenza (assoluta o relativa) della stessa
modalità rappresentata
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
Diagramma a barre
Livello di conoscenza della lingua inglese
ni
14
Buono
19
Discreto
23
Sufficiente
28
Mediocre
11
Scarso
5
30
Eccellente
TOTALE
Eccellente
Buono
Discreto
Mediocre
Sufficiente
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
Scarso
0
5
10
15
20
25
100
Istogramma
L’istogramma è un grafico costituito da barre non distanziate (con basi
uguali o diverse), dove ogni barra possiede un’area proporzionale alla
corrispondente frequenza della classe.
8
7
6
5
4
3
2
1
0
Esempio di
Istogramma con
classi di uguale
ampiezza
10
30
50
70
90
Per la costruzione di un ISTOGRAMMA si disegna, per ogni classe di valori
del carattere statistico, un segmento (barra) di larghezza pari all’ampiezza
della classe di valori considerata e di altezza pari alla densità di frequenza
della stessa classe
Statistica 3 CFU – Sc. Motorie Docente: Paolo Mazzocchi
Istogramma
Se la distribuzione in classi presenta classi
di ampiezza differente è necessario calcolare
la densità di frequenza data dal rapporto tra
ni
di=
ai
la frequenza e l’ampiezza della classe
xi
ni
αi
di=ni/ αi
18-24
24-26
26-28
28-30
55
17
20
22
6
2
2
2
9,1
8,5
10
11
Totale
114
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
xi
ni
αi
di
18-24
55
6
9,1
24-26
17
2
8,5
26-28
20
2
10
28-30
22
2
11
Istogramma
12,00
10,00
8,00
6,00
4,00
2,00
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
30
28
26
24
22
20
0,00
18
densità di frequenza di=ni/ai
•
Altro esempio Istogramma
classi di età
amp. classe ni
freq. ni
densità h
dij
0-5
5
17
3,4
5-15
10
40
4,0
15-30
15
37
2,5
30-35
5
6
1,2
Ampiezza diversa delle classi:
di = densità si ottiene come rapporto tra
la frequenza e l’ampiezza della classe.
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
Esempio Istogramma
classi di età
amp. classe ai
freq.ni
densità di
0-5
5
17,0
3,4
5-15
10
40,0
4,0
15-30
15
37,0
2,5
30-35
5
6,0
1,2
Nota:.
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
Misure di sintesi
Come “leggere” l’informazione statistica
Per comprendere i contenuti dell’informazione statistica occorre
utilizzare delle “misure di sintesi”. Le principali misure utilizzate
riguardano:
a)
La tendenza centrale. Si vuole trovare un valore che sia
rappresentativo dell’intera distribuzione. Le tendenza centrale di
una distribuzione è misurata dalla moda, dalla mediana e dalla
media.
b) La dispersione. Si vuole verificare di quanto i valori osservato
oscillano intorno al valore centrale. Misure della dispersione sono
il campo di variazione, i quartili, la varianza, lo scarto
quadratico medio e il coefficiente di variazione.
NOTA: quando i dati vengono sintetizzati si ha una perdita di informazione,
quindi occorre fare molta attenzione all’interpretazione degli stessi ed
utilizzare sempre entrambe le misure di sintesi.
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
La moda
La moda o valore modale di un carattere statistico si
identifica con la modalità del carattere che si presenta
con la massima frequenza
Per il calcolo della moda è necessario distinguere:
•Distribuzione di frequenza semplice
•Distribuzione di frequenza con classi di valori
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
MODA: distribuzione di frequenza semplice
Numero di figli rilevati su un campione di 100 famiglie
xi
Ni
(numero di figli)
0
18
28
35
12
7
100
1
2
3
4
Totale
Distribuzione
di frequenze
La moda di questa distribuzione è rappresentata dalla
modalità numero di figli pari a 2, in quanto corrisponde alla
modalità che presenta la frequenza più elevata (35)
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi
MODA: distribuzione di frequenza conclassi di valori
In questo caso si individua la modalità che presenta la densità
di frequenza più elevata.
xi
(peso alla nascita
espresso in grammi)
ni
ai
di=ni/ai
[1000-1500)
10
500
10/500=0,02
[1500-1800)
150
300
150/300=0,50
[1800-2000)
140
200
180/200=0,70
[2000-2500)
100
500
100/500=0,20
[2500-3000)
120
500
120/500=0,24
[3000-5000]
350
2000
350/2000=0,17
Totale
870
La moda si individua nella classe [1800-2000) (viene definita
classe modale), in quanto presenta la densità di frequenza più
elevata (0,70).
Statistica 3 CFU – Sc. Motorie
Docente: Paolo Mazzocchi