Sensori di Temperatura

Diploma in Ingegneria Elettronica
Corso di Sensori e Trasduttori
Sensori di Temperatura
(raccolta di lucidi)
1
Trasmissione del Calore ...
Le due proprietà fondamentali del calore sono che (i) una volta prodotto è
impossibile risalire alla sua origine e (ii) non può essere contenuto ma fluisce
spontaneamente dalla parte più calda a quella più fredda del sistema. La sua
trasmissione può avvenire in tre distinti modi:
• per conduzione sfrutta il contatto fisico fra i corpi di modo che le particelle nel
corpo più caldo agitate termicamente si muovono e trasferiscono
(raffreddandosi) energia cinetica a quelle del corpo più freddo
(riscaldandolo); in tal caso la potenza termica
dQ dt
è
proporzionale al gradiente termico dT dx ed alla sezione A del
materiale tramite la conduttività termica k :
dQ
dT
= −k ⋅ A⋅
dt
dx
 W 
k
 m ⋅ K 
alto per i conduttori
basso per gli isolanti
2
• per convezione sfrutta un agente intermedio (liquido o gas) per trasportare il
calore da un corpo più caldo ad un corpo più freddo. La
convezione può chiaramente essere naturale o forzata; in tal
caso la potenza termica dQ dt è proporzionale al gradiente
termico dT ed all’area A tramite il coefficiente convettivo α :
 W 
α 2

m ⋅ K 
dQ
= α ⋅ A ⋅ dT
dt
• per radiazione è legato alle vibrazioni degli atomi e delle molecole che hanno
una energia cinetica media che è rappresentata dalla sua
temperatura assoluta; questa vibrazione è sorgente di un campo
elettromagnetico che si propaga alla velocità della luce ed è
governata dalla legge di Plank; in questo caso la potenza della
radiazione elettromagnetica per unità di lunghezza d’onda λ è
proporzionale all’emissività ε (λ ) dell’oggetto:
Wλ =
ε ( λ ) ⋅ C1
(
π ⋅ λ5 e C 2
λT
−1
)
[
C1 = 3.74 ⋅ 10 −12 W ⋅ cm 2
0 ≤ ε(λ ) ≤ 1
C 2 = 1.44
[cm ⋅ K ]
]
3
… Temperatura e Capacità Termica
La temperatura è la grandezza fisica più comunemente misurata in ambito
industriale; essa determina la direzione del flusso di calore, la sua misura
avviene in modo statistico ed è fortemente influenzata da diverse variabili
(contatto termico, risposta nel tempo,…)
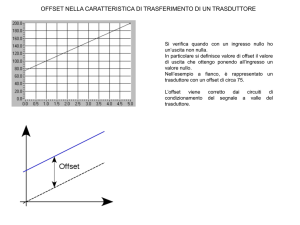
E’ chiaro che il dispositivo utilizzato per
questa misura deve influire il meno possibile
sulla grandezza da rilevare (devono essere
ridotti gli “effetti di carico”). Questo significa
che la misura della temperatura con un
sensore sarà accurata se la capacità termica
(a volte detta massa termica) del sensore è di
La capacità termica di un oggetto
rappresenta la quantità di calore
che esso può immagazzinare sotto
forma di energia cinetica. Essa può
essere definita tramite calore
specifico c [J/kg·K] e massa m del
materiale:
C =c⋅m
molto inferiore rispetto alla capacità termica
del misurando.
4
Errori nella Misura
Sono molte le cause che possono produrre errori nella misura di una
temperatura; per rendersene conto basta tenere presente che la temperatura
rilevata:
• è una media della temperatura del corpo
• dipende dagli errori dello strumento
• è legata al tempo di misura
• dipende dalla lettura dell’operatore
• è influenzata dalle capacità termiche del sensore e del corpo
E’ chiaro che solo una comprensione completa delle tecniche di rilevazione
(trasduzione) può produrre una misura di temperatura estremamente accurata
5
Scale di Temperatura
Il processo di standardizzazione delle scale di temperature è stato lungo e laborioso
(1700-1900). Esso ha riguardato la scelta dei punti di calibrazione e la suddivisione
delle scale. Oggi le scale più comuni sono quelle Celsius, Kelvin, Fahrenheit e
Rankine anche se le più utilizzate sono certamente le prime due.
zero assoluto
punto di congelamento
H 2O
punto di ebollizione
H 2O
u Celsius
-273.15
0
100
u Kelvin
0
273.15
373.15
u Fahrenheit
-459.67
32
212
427.67
671.67
u Rankine
0
6
La Scala Internazionale di Temperatura
Il problema della realizzazione di una scala di temperatura univoca è stato
affrontato per la prima volta a livello internazionale solo nel 1927 (CIPM). In
quella occasione fu stabilita la costituzione di una scala di temperature
internazionale (IPTS - International Practical Temperature Scale) che ha subìto
ulteriori revisioni nel corso di conferenze successive (1948, 1954, …,1990). In
pratica l’IPST è lo standard a cui i vari paesi devono riferirsi per le misure di
temperatura che:
• fissa i punti di riferimento per la calibrazione (punto di congelamento, punto
triplo, ecc.)
• definisce le equazioni ed i metodi da utilizzare per calcolare le temperature
intermedie (interpolazione)
• definisce gli strumenti da usare nei diversi range di temperatura
7
L’IPST suddivide l’intero campo di variazione della temperatura in quattro range
predefiniti; per ognuno di essi precisa i punti fissi, le equazioni di interpolazione e gli
strumenti per la misura:
• Range I:
da
13.8 K (-259.34 °C)
a
273.15 K (0 °C)
• Range II:
da
273.15 K (0 °C)
a
903.89 K (630.74 °C)
• Range III:
da
903.89 K (630.74 °C) a
• Range IV:
oltre 1337.58 K (1064.43 °C)
1337.58 K (1064.43 °C)
E’ chiaro che i valori che delimitano gli intervalli e le formule di interpolazione da
utilizzare hanno subìto delle variazioni nel corso degli anni (e nel susseguirsi delle
conferenze) in conseguenza del fatto che con il progredire della tecnica si sono
ottenuti punti di riferimento sempre più stabili e precisi.
8
Storia dei Sensori di Temperatura
Anche se il primo sensore di temperatura si può far risalire a Galileo (1600),
dovranno passare circa duecento anni per assistere alle grandi scoperte che
porteranno alla realizzazione di sensori elettrici. Nel 1821 viene scoperto che due
giunzioni dissimili a diversa temperatura possono generare una corrente elettrica
(Seebeck); in quegli stessi anni si osserva che la resistenza elettrica dei metalli
varia con la temperatura (Davy)) e nel 1871 viene realizzato il primo prototipo di
termometro al platino (Siemens). Intorno al 1900 si scoprono le proprietà dei
semiconduttori e più tardi si cominciano a realizzare sensori di temperatura con
circuiti integrati.
u 1800
u 2000
u 1900
effetto Seebeck
termistore
Sensore I.C.
effetto termoresistivo
Pt 100
9
Misura della Temperatura
•
La misura di temperatura richiede la trasmissione di una piccola quantità di
energia termica dall’oggetto al sensore; nei trasduttori elettrici l’energia
termica è convertita in un segnale elettrico (sensori piroelettrici, sensori
termoelettrici, sensori ottici, ecc).
•
Ci sono due modi di procedere nella misura della temperatura: per equilibrio e
predittivo. Nel primo metodo la misura è completata quando non c’è più
gradiente termico fra corpo e sensore, nel secondo è ricavata attraverso
l’andamento della temperatura senza che il punto di equilibrio sia mai
raggiunto.
•
I sensori possono risalire alla temperatura per contatto o senza contatto; ai
primi, che funzionano per conduzione termica, è richiesto un basso calore
specifico ed un’alta conduttività termica, ai secondi, che funzionano per
radiazione termica, sono richiesti spessori ridotti e superfici sensibili elevate
10
Termometro
100
• liquido: è il sensore di temperatura per antonomasia e
sfrutta la dilatazione termica di un liquido in uno stelo; è
fragile, lento nella risposta ed ha una risoluzione che
0
dipende dalla sua lunghezza.
• a colori termosensibili: si realizza con superfici ricoperte
di pigmenti finemente suddivisi che si oscurano quando
viene raggiunta la loro temperatura di fusione. E’
utilizzato per misure in luoghi pericolosi o difficili da
raggiungere; ha una bassa risoluzione e produce
un’irreversibile variazione di colore quando si supera la
loro temperatura di soglia. Non è riusabile.
11
Sensore di Temperatura Bimetallico
Si tratta di un trasduttore meccanico a dilatazione termica che si realizza saldando
fra loro due metalli diversi e collocando ad una estremità una lancetta. Dato che i
due metalli esibiscono coefficienti di espansione termica differenti, una variazione
di temperatura produrrà una curvatura che dipenderà dallo spessore tA/B e dalle
costanti di elasticità KA/B delle lamine e dai coefficienti di espansione termica αA/B.
S = f (t A , t B , K A , K B , α A , α B )
100
0
200
A
B
tA
αA
t B αB
T2 > T1
T1
T2 < T1
S
α A > αB
S
300
400
[°C]
Questo sensore è economico ma presenta problemi
di isteresi ed è comunque poco accurato. Viene
quindi utilizzato per misure grossolane.
12
Pirometro
Si tratta di un trasduttore elettrico ad infrarossi che si fonda sulla trasmissione del
calore per radiazione elettromagnetica e sulla legge di Plank che la regola.
Teoricamente questo sensore dovrebbero
misurare la temperatura quando tutta la
radiazione termica della sorgente colpisce il
dispositivo.
Di conseguenza, per essi occorre far riferimento alla legge di Stefan-Boltzmann,
che è ottenuta dalla legge di Plank per integrazione su tutte le lunghezze d’onda:
W = κ ⋅ σ ⋅T
4
dove κ ( < 1 ) è il potere emissivo per tutte le lunghezze d’onda e
σ = 5.670 ⋅ 10 −8 W ⋅ m − 2 K −4 è la costante di Stefan-Boltzmann
In realtà il pirometro non funziona per tutte le lunghezze d’onda poichè le lenti o
gli specchi utilizzati per focalizzare la radiazione sul sensore costituiscono dei
veri e propri filtri ottici.
13
Questi materiali, infatti, sono generalmente opachi per onde lunghe e onde corte
ma sono trasparenti nel visibile e nel vicino infrarosso per cui la legge di Plank non
viene integrata su tutte le lunghezze d’onda.
Il pirometro produce una risposta
approssimativamente proporzionale a T 4 ed è
pertanto inerentemente non lineare. E’ un
sensore non invasivo, costoso e molto stabile
che permette di misurare anche temperature
elevate; la sua sensibilità è più accentuata alle
alte temperature che non alle basse. E’ usato
per temperature anche superiori ai 1450 °C dove
altri sensori hanno vita breve ed è utile anche nel
controllo di processi la cui temperatura varia da
200-1450 °C ed in cui è essenziale la mancanza
di contatto con il sistema.
14
Sensori a Variazione di Resistenza
Si tratta di un trasduttore elettrico che sfrutta la proprietà dei metalli di variare la
conducibilità elettrica con la temperatura. I termoresistori o RTD
(Resistance Temperature Detectors) usano in genere come materiale
il platino, proprio per le sue caratteristiche di lunga durata, stabilità e
riproducibilità. In generale la resistenza di un metallo è una funzione complessa della
temperatura anche se per la maggior parte di essi lo sviluppo in serie di potenze
produce buoni risultati. Nel caso del platino l’equazione utilizzata è quella di
Callendar-van Dusen (che viene corretta in base all’IPTS-68):
con A, B e C costanti e dipendenti dalle proprietà
[
R = Ro 1 + At + Bt 2 + C ( t − 100 ) t 3
]
del platino utilizzato per realizzare il sensore e
Ro=100 Ω
E’ utile osservare che per il range di temperature che va da 0 a 630 °C, la funzione di
trasferimento del platino non dipende dalla potenza terza della temperatura ma si
riduce all’equazione di Callendar che si compone di un termine lineare e di un
15
termine quadratico che comincia a pesare oltre
R
un certo valore di temperatura:
R = Ro
[1 + At + Bt ]
2
300
200
Per temperature sotto il punto di congelamento
100
dell’acqua e fino a -200 °C occorre portare in
conto la correzione di van Dusen e considerare
T
0
200
400
600
800
le potenze fino al terzo ordine.
Gli RTD sono sensori di temperature per misure assolute; hanno una buona sensitivity,
sono molto stabili e richiedono un circuito di interfaccia semplice.
Purtroppo sono non lineari e presentano bassi valori di resistenza; per ridurre il primo
inconveniente si utilizzano opportune tecniche di compensazione mentre per superare
il secondo inconveniente bisogna fare molta attenzione alla procedura di misura
(collegamento a 4 fili e metodi a ponte). La RTD al platino è il dispositivo più accurato
e stabile nel range di temperatura 0 - 500 °C anche se può misurare temperature fino a
800 °C (in genere per valori maggiori di 600 °C si usano RTD al Tungsteno).
16
Termistori
Si tratta di un trasduttore elettrico che sfrutta le proprietà dei semiconduttori di variare
la conducibilità elettrica con la temperatura. I termistori (Thermal Resistor)
possono avere coefficienti di temperatura (TCR) negativi
(termistori NTC) o positivi (termistori PTC). In generale la funzione
di trasferimento di un termistore NTC può essere approssimata da una
funzione esponenziale a quattro parametri piuttosto complessa anche se molto
spesso si ricorre ad un’espressione semplificata del tipo:
R = Ro
e β (1 T −1 To
)
a due parametri, dove Ro è il valore di resistenza alla
temperatura di riferimento di 25 °C
mentre il TCR è dato da: α =
1 dR
= −βT − 2
R dT
Dall’analisi del coefficiente di temperatura α si evince chiaramente che i termistori
sono più sensibili alle basse temperature visto che la loro sensibilità si riduce
notevolmente al crescere della temperatura.
17
E’ utile osservare che per misure più precise si
può ricorrere all’equazione di Steinhart-Hart che
produce accuratezze fino all’ordine di 0.02 °C.
Il termistore PTC, invece, ha una curva
Pag 474
difficilmente approssimabile con un’equazione
matematica per cui essa è definita dai costruttori
mediante un certo numero di punti prestabiliti:
• resistenza a temperatura ambiente R25
• temperatura di transizione Tτ
1 dR
R dT
• capacità termica e tensione massima
• TCR definito come α =
I termistori PTC hanno un intervallo di funzionamento ristretto e sono usati per la
protezione da sovraccarichi e da surriscaldamento.
18
Per la misura di temperatura, invece, si utilizzano quasi sempre i termistori NTC.
I termistori sono molto più sensibili degli RTD (da 103 a 106 volte superiore) e
funzionano (gli NTC) in un range di temperature che va da -100 a 500 °C circa.
Presentano una impedenza molto elevata e non richiedono particolari procedure
di misura (collegamento a 2 fili). Purtroppo sono fortemente non lineari.
19
Sensori Integrati
Sono trasduttori che utilizzano le proprietà delle giunzioni a semiconduttore
(diodi e transistor) di avere la tensione o la corrente fortemente
dipendente dalla temperatura; questa dipendenza è
peraltro notevolmente lineare.
I
V
Nel caso di un diodo la relazione corrente-tensione porta ad
una relazione tensione-temperatura del tipo:
V=
Eg
q
−
2kT
( lnK − lnI )
q
dove Eg è il gap di energia del materiale K è una
costante del materiale indipendente dalla temperatura, q
è la carica dell’elettrone e k è la costante di Boltzmann.
Quando la giunzione è sottoposta ad una corrente
costante la tensione è linearmente dipendente dalla
temperatura e la sensibilità del dispositivo è data da:
r =−
2kT
( lnK − lnI )
q
20
Il discorso è equivalente nel caso di un transistor anche se
I
per un corretto funzionamento è richiesto un opportuno
circuito. D’altronde, visto che la corrente nel transistor è data
R
E
V
dalla relazione I = E - V R una resistenza R stabile è
raccomandabile (MTS102 della Motorola Semiconductor).
Partendo da queste semplici configurazioni e sfruttando le proprietà dei
semiconduttori vengono realizzati sensori di temperatura più complessi ( Integrated
Circuit Sensor) che contengono al loro interno opportuni circuiti integrati.
Essi utilizzano un certo numero di transistor identici connessi
fra loro e sfruttano la relazione fra la tensione base-emettitore
e la corrente di collettore:
∆V BE
kT I c1
=
ln
q I c2
di modo che per valori fissati di corrente la
tensione dipende solo dalla temperatura.
21
In questo modo si realizzano sensori di temperatura lineari
con uscita in tensione (LM35CZ della National
I
AD590
Semiconductor) o in corrente (AD590 della Analog
Devices), poco costosi ed accurati ma che funzionano in
un range di temperatura limitato (da -65 a 150 °C circa).
22
Termocoppie
Sono trasduttori che utilizzano le proprietà termoelettriche
TF
derivanti dall’accoppiamento di due conduttori dissimili
B
Tc
V
posti a temperature diverse; Il loro funzionamento è basato
TF
sull’effetto Seebeck
A
E S AB = k S AB (T ) ⋅ ∆T
secondo cui la tensione al giunto freddo è
[µV
°C ]
proporzionale alla differenza di temperatura fra le due
giunzioni. Purtroppo la dipendenza non lineare del
K S AB
coefficiente di Seebeck dalla temperatura finisce per
inficiare la relazione di “linearità” fra temperatura e
[° C ]
T
tensione.
Per un uso adeguato di questi sensori e per una loro connessione corretta è utile
fare riferimento alle tre leggi fondamentali sulle termocoppie che tornano utili in molte
situazioni pratiche:
23
1. Legge dei circuiti omogenei
A
in un circuito omogeneo nessun gradiente di
i=0
T1
T2
temperatura potrà produrre una tensione
A
netta e quindi una corrente termoelettrica.
B
T2
T1
V1
2. Legge dei conduttori intermedi
A
in un circuito composto da un qualsiasi
numero di materiali dissimili la tensione netta
C
sarà nulla se tutte le giunzioni sono alla
stessa temperatura.
B
B
T3
T3
T1
T2
V1
A
24
3. Legge delle temperature successive
Se V1 è la tensione di Seebeck prodotta da due giunzioni a temperature T1 e
T2 e V2 è la tensione di Seebeck prodotta da due giunzioni a temperature T2
e T3 allora la tensione di Seebeck prodotta da due giunzioni a temperatura T1
e T3 sarà pari a V 3= V1 + V2.
B
T1
B
V1
A
B
T3
T2
V2
A
T3
T1
V3
A
25
La realizzazione e l’uso delle termocoppie presenta in pratica due problemi
fondamentali:
• la necessità di inserire il blocco di condizionamento e misura (e quindi delle
ulteriori giunzioni) senza alterare il risultato
• la necessità durante la misura di mantenere la temperatura del giunto freddo
ad un valore costante e noto.
B
Cu
Questo obiettivo si raggiunge:
1) ponendo le giunzioni derivanti dal collegamento alla
V
stessa temperatura (che per la II legge non produrrà
T rif
Tx
Cu
A
nessuna tensione netta)
Vx
2) misurando la temperatura di riferimento senza forzarla a
V ref
0 °C tramite un bagno di ghiaccio
3) prima ricavando la tensione incognita Vx come somma di
V e di Vref (per la III legge) e poi convertendo in temperatura
T0
T ref
(
Tx
) (
V x − V o = V x − V ref + V ref − V o
)
26
Le termocoppie possono essere suddivise in due gruppi fondamentali: quelli a
metallo nobile e quelle a metallo vile. Le prime sono molto costose e presentano
Tipo
Coefficiente
di Seebeck
Metalli
[µ V
T
K
J
E
R,S
Cu-Con
Ni-Cr
Fe-Con
Ni/Cr-Con
Pt/Rh-Pt
°C ]
38
40
50
59
10
un coefficiente di Seebeck
Range di
Funzionamento
basso mentre le seconde hanno
[° C ]
un coefficiente più elevato; in
0 ÷ 370
-200 ÷ 1260
0 ÷ 760
-200 ÷ 900
0 ÷ 1480
può inficiare il risultato della misura dato che
entrambi i casi occorre agire
con molta cautela poiché la
presenza del rumore
V [mV]
E
l’uscita in tensione è sempre dell’ordine
dei µV. A causa dell’andamento non lineare
della curva T-V è necessario ricorrere ad un
60
J
40
K
N
opportuno algoritmo interpolatore:
20
R
T = a o + a1V + a 2V + ...
2
0
500
1000
S
2000
T [°C]
27
il cui ordine varia con il tipo di termocoppia ed i cui coefficienti vengono in
genere ricavati per via empirica. Nel caso in cui si debba operare in intervalli
ristretti il metodo più semplice ed utilizzato è quello della linearizzazione della
curva.
L’utilizzo delle termocoppie è indicato per l’ampio range di temperatura
misurabile e per la loro notevole resistenza meccanica. D’altronde la
possibilità di ricorrere ad un numero elevato di metalli permette il loro uso in
ambienti ostili.
28
Conclusioni ed ...
I
Pirometro
RTD
Termistore
S. Integrato
Termocoppia
• non invasivo
• sensibile
• veloce
• molto stabile
• molto stabile
• molto sensibile • economico
• temperature
• molto accurato • collegamento a • lineare
• ampia scelta
• abbastanza
• robusta
elevate
• range esteso
• accurato
2 fili
• economico
• range esteso
lineare
• non lineare
• lento
• non lineare
• costoso
• costoso
• range limitato
• collegamento
• fragile
• range molto
limitato
• scelta limitata
• non lineare
• misure relative
• misure difficili
a 4 fili
29
… Applicazioni
Sensori
Misure
• Termocoppie
• Forni ad induzione, forni per uso alimentare
• Sensori Integrati
• Celle frigorifere, compensazione di
• Pirometri
temperatura in dispositivi di qualità
• RTD
• Vetro fondente
• Termistori
• Processi fotochimici, monitoraggio
temperatura sostanze alimentari
• Sistemi di riscaldamento, elettronica
industriale e di consumo, telecomunicazioni
30