ELETTROMAGNETISMO.
L’esperienza di Hans Christian Oersted.
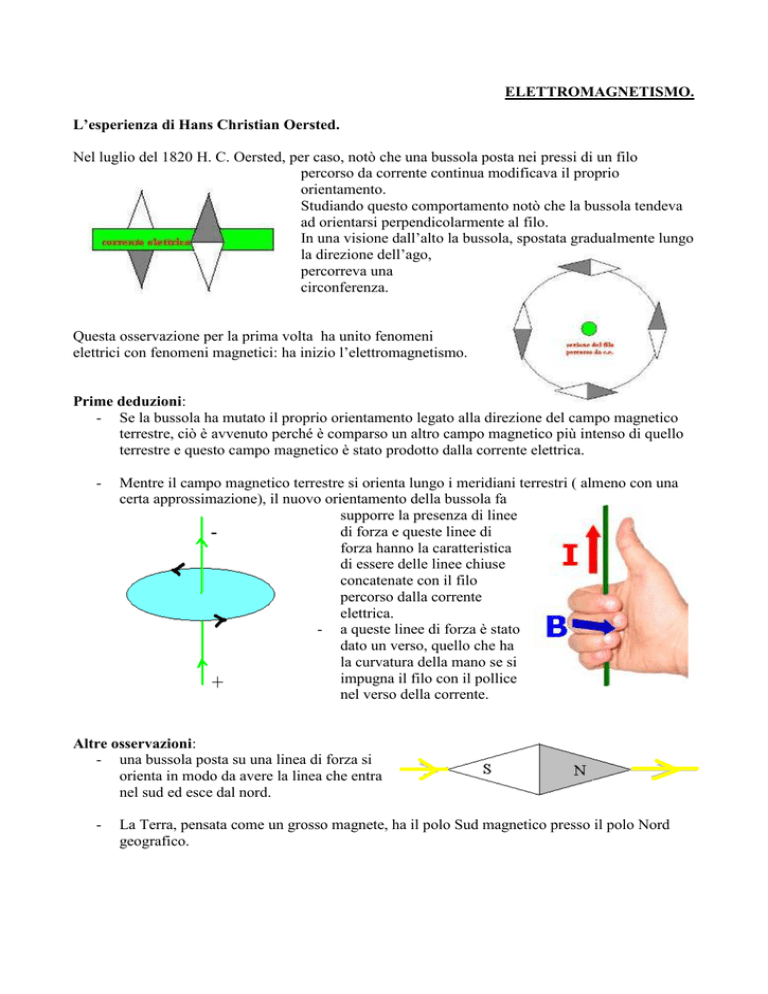
Nel luglio del 1820 H. C. Oersted, per caso, notò che una bussola posta nei pressi di un filo
percorso da corrente continua modificava il proprio
orientamento.
Studiando questo comportamento notò che la bussola tendeva
ad orientarsi perpendicolarmente al filo.
In una visione dall’alto la bussola, spostata gradualmente lungo
la direzione dell’ago,
percorreva una
circonferenza.
Questa osservazione per la prima volta ha unito fenomeni
elettrici con fenomeni magnetici: ha inizio l’elettromagnetismo.
Prime deduzioni:
- Se la bussola ha mutato il proprio orientamento legato alla direzione del campo magnetico
terrestre, ciò è avvenuto perché è comparso un altro campo magnetico più intenso di quello
terrestre e questo campo magnetico è stato prodotto dalla corrente elettrica.
-
Mentre il campo magnetico terrestre si orienta lungo i meridiani terrestri ( almeno con una
certa approssimazione), il nuovo orientamento della bussola fa
supporre la presenza di linee
di forza e queste linee di
forza hanno la caratteristica
di essere delle linee chiuse
concatenate con il filo
percorso dalla corrente
elettrica.
- a queste linee di forza è stato
dato un verso, quello che ha
la curvatura della mano se si
impugna il filo con il pollice
nel verso della corrente.
Altre osservazioni:
- una bussola posta su una linea di forza si
orienta in modo da avere la linea che entra
nel sud ed esce dal nord.
-
La Terra, pensata come un grosso magnete, ha il polo Sud magnetico presso il polo Nord
geografico.
ELETTROMAGNETISMO
L’esperienza di Faraday
Qualche anno dopo C. Oersted, M.Faraday eseguì una esperienza altrettanto fondamentale per la
comprensione dei fenomeni magnetici:
Facendo passare un conduttore all’interno di un magnete, egli notò che, quando il
conduttore era percorso da corrente elettrica, una forza agiva sul conduttore stesso
con le seguenti caratteristiche:
1. questa forza era perpendicolare al verso della corrente ( + -);
2. questa forza era perpendicolare alla direzione del campo magnetico (nord
sud);
3. questa forza era massima quando il verso della corrente era perpendicolare
alle linee di forza del campo magnetico, per diventare nulla quando il
verso della corrente diventava parallelo alle linee di forza del campo
magnetico.
4. questa forza era proporzionale alla lunghezza del filo compreso tra i poli
del magnete.
Questa esperienza ha permesso di definire l’unità di misura che utilizzeremo per
esprimere l’intensità del campo magnetico anche se la sua denominazione è
vettore induzione magnetica che si indica con la lettera B.
Formula :
F i·B·l
o in modo più operativo
F i·B·l·sin
essendo: F
la forza che agisce sul filo
i
l’intensità della corrente espressa in Ampere
B
il vettore induzione magnetica ( l’intensità del campo
magnetico)
l
la lunghezza del filo compreso tra i poli del magnete
a l’angolo tra il verso della corrente e le linee di forza del campo
magnetico.
Dalla precedente formula si ottiene la formula inversa:
B
F
che permette di definire il Tesla
i·l
(T)
1N
( si ha un campo magnetico
1A·1m
di 1 T quando un conduttore, posto
perpendicolarmente al campo
magnetico,e percorso da una corrente di
un Ampere, subisce una forza di un
Newton).
Regola della mano destra: questa regola empirica permette di conoscere la direzione della forza
disponendo le tre dita della mano destra ( pollice, indice, medio) uno perpendicolare agli altri due;
il pollice indica la direzione della corrente (Ampére), l’indice indica la direzione del campo
magnetico (B ), e il medio indica la direzione verso della forza ( F ),
1T
ELETTROMAGNETISMO
L’esperienza di Ampére
Dalle precedenti esperienze di Oersted e di Faraday ormai si era dedotto che una corrente elettrica
genera attorno a sé un campo magnetico.
Ampére, quindi, dedusse che due correnti elettriche, generando due campi magnetici, in qualche
modo si sarebbero comportate come due magneti manifestando fenomeni reciproci di attrazione o
repulsione.
L’esperienza di Ampére consiste nel
verificare la presenza della forza
attrattiva o repulsiva tra due correnti
parallele.
3.
Le conclusioni furono:
1.
Due correnti elettriche
concordi si attraggono;
2.
due correnti elettriche discordi
si respingono.
Il calcolo di questa forza ha portato alla seguente formula:
i ·i ·l
F k· 1 2
d
essendo : i1 e i2
l
d
K
4.
l’intensità delle due correnti in Ampére
la lunghezza del tratto dei due fili
la distanza tra i due fili.
una costante che in base alle nostre unità di misura viene definita
uguale 2 ∙ 10-7 oppure µ0 / 2 essendo µ0 = 4··10-7, detta
permeabilità magnetica del vuoto. (N/A2)
Questa formula ha permesso di dare una definizione di 1 A: due fili sono percorsi dalla
corrente di 1 A quando, posti alla distanza di 1m, per un tratto di filo lungo 1m, si attraggono
o si respingono con la forza di 2·10-7 N.
5.
L’esperienza di Ampére ha
permesso di avanzare delle
ipotesi sulla struttura atomica
di un magnete, ipotesi che
giustificano il comportamento
dei magneti stessi:
a) un magnete è costituito da
strutture microscopiche (domini di
Weiss) in cui gli atomi hanno
elettroni che ruotano su orbite più o meno complanari, nello stesso verso;
b) questo fatto causerebbe una corrente superficiale attorno al magnete che causerebbe la attrazione
o la repulsione con altri magneti.
Nord
Nord
c) se questa corrente gira in senso antiorario, il polo che
guardiamo è il polo nord, se invece gira in senso orario,
guardiamo quello sud: i due poli sono inscindibili perché
sono la stessa corrente osservata da due punti di vista
opposti.
6) Questa esperienza inoltre è stata anche alla base delle riflessioni di A.Einstein in quanto è una
delle situazioni della non applicabilità della relatività newtoniana ai fenomeni elettromagnetici: se
un osservatore fosse in moto costante tra i due fili, con velocità uguale a quella della corrente,
dovrebbe valutare le cariche della corrente ferme e quindi soggette alla forza di Coulomb, con
un’azione repulsiva, invece l’esperienza afferma che c’è una attrazione…
Rappresentazione dell’azione magnetica tra conduttori percorsi da corrente elettrica:
ELETTROMAGNETISMO
La corrente elettrica causa un campo magnetico
Le correnti elettriche generano campi magnetici
Premesse:
l’esperienza di Oersted aveva fatto notare che una
corrente influenza il comportamento di una bussola; da
questa osservazione si era dedotto che una corrente
elettrica genera un proprio campo magnetico; a questo
campo magnetico si era dato un verso con l’uso della
regola della mano destra ….
l’esperienza di Ampére aveva confermato che le
correnti elettriche generano un campo magnetico; per
l’esperienza di Ampére si era data anche una formula
che permetteva il calcolo della forza interagente tra le due correnti elettriche:
F
0 i1 ·i2 ·l
·
2 d
Calcolo dell’intensità di un campo magnetico prodotto
da una corrente elettrica
Dopo l’aspetto qualitativo, esistenza e direzione del
campo magnetico, ora si propongono le formule che
operativamente permettono di calcolare l’intensità del
vettore induzione magnetica in generale e in qualche caso
particolare.
Presentiamo innanzitutto la formula di Ampére-Laplace che può risultare alquanto criptica per i non
addetti ai lavori, ma che esprime la sintesi di questi due studiosi sull’argomento; questa formula
permetterebbe di calcolare l’intensità del campo magnetico, generato da una corrente elettrica che
percorre un circuito di forma qualunque, in un qualsiasi punto dello spazio:
Formula di Ampére-Laplace:
B
0 ut ur
i
dl
4 r 2
che deve essere così interpretata:
il circuito elettrico lo si può ritenere formato da tanti
tratti, relativamente piccoli, che noi indicheremo con
dl;
ciascuno di questi tratti di circuito, percorso da corrente
elettrica, genererà un campo magnetico che nel punto P avrà una certa intensità;
la somma di tutti i valori dell’intensità del campo magnetico ottenuti per ciascun tratto dl del
circuito darà il valore del campo magnetico richiesto; questa somma è espressa dal simbolo di
integrazione , che rappresenta una esse stilizzata ( somma) mentre il cerchietto sovrapposto
sta ad indicare che questa somma è fatto lungo un percorso chiuso. B è il vettore induzione
magnetica del c.m. in un punto P;
Gli altri valori sono:
/4 = costante che nel vuoto vale 10-7;
i = intensità della corrente che percorre una linea chiusa;
r = distanza variabile del punto P da un tratto della linea chiusa di lunghezza infinitesima dl;
dl = tratto infinitesimo della linea chiusa, considerato un segmento di retta tangente;
utur = prodotto vettoriale dei due vettori unitari che indicano la direzione il primo della
corrente e il secondo la direzione della retta che congiunge il tratto dl del circuito e il punto P:
operativamente corrisponde al seno dell’angolo tra queste due direzioni.
1) campo magnetico prodotto da una corrente elettrica di un filo
rettilineo:
formula per sapere l’intensità del campo magnetico ad una distanza di r dal
filo:
B
0i
2 r
essendo:
0 = la costante di permeabilità 4·10-7
i = l’intensità della corrente in Ampére
r = la distanza del punto dal filo.
Questa formula è anche detta Legge di Biot-Savart.
Questa formula si può ottenere dalle formule di Faraday e di Ampère:
F = i∙B∙l
i i l
F= 0 1 2
2 r
0 i1 i2 l
i B l
2 r
forza esercitata da un c.m. su un filo percorso da c.e.
forza esercitata dai c.m. prodotti da c.e. parallele
B
0i
2 r
c.m. prodotto da una corrente a distanza r dal filo.
2) campo magnetico prodotto da una corrente elettrica che circola in una spira circolare:
B
In un punto P dell’asse
della spira
0 ·i·R 2
B
3
2 R2 y2
Nel centro della spira (y =
0)
·i
B 0
2·R
Se le spire sono n ( bobina di n spire),il valore precedente è da moltiplicare per n.
3) campo magnetico all’interno di un solenoide:
Se le spire sono allineate ordinatamente, se il raggio
delle spire è relativamente più piccolo della
lunghezza della loro disposizione, se il passo tra una
spira è l’altra è piccolo, allora si ha un solenoide; al
suo interno il campo magnetico è ritenuto uniforme
e la sua intensità è data dalla formula
·i·N
B o
essendo i = intensità di corrente,
l
N = numero delle spire
l = lunghezza del
solenoide.
Talvolta, al posto del rapporto N/l, si scrive n
indicando con questa lettera la densità delle spire (numero di spire per unità di lunghezza).
Momento di una spira percorsa da corrente elettrica in un campo magnetico.
Se una spira, percorsa da corrente elettrica, e libera di ruotare attorno ad
un asse, è attraversata da linee di forza di un campo magnetico, essa può
essere soggetta ad una rotazione.
Nella prima figura ipotizza una spira disposta perpendicolarmente alle
linee di forza magnetiche (
si ricorda che la direzione
della spira è perpendicolare
alla superficie delimitata
dal circuito), in questo caso
i tratti AB e CD sono
perpendicolari alla linee di
forza e quindi sono
soggetti alla forza F = B·i·l
in cui
B è il vettore induzione
magnetica;
i è l’intensità della corrente
l è la lunghezza del tratto AB o del tratto CD.
Se la corrente percorre la spira da D verso A, le forze che agiscono sui
tratti AB e CD sono parallele, ma discordi, quindi eserciteranno una
coppia sulla struttura della spira ( seconda figura) causandone la rotazione fino alla posizione
indicata nella terza figura, nella quale le due forze, sempre opposte, agiscono su una medesima
retta.
Calcolo del momento:
Per momento di una coppia si intende il prodotto della forza per il braccio, ovvero per la distanza
delle rette di azione delle due forze.
Nella seconda figura è evidente che il braccio in quella situazione corrisponde alla lunghezza del
tratto di circuito BC; mentre nella terza figura il braccio è nullo.
Per le situazione intermedie, come può dedursi dalla figura qui a fianco, si nota che il braccio è
dato dal prodotto della lunghezza del tratto BC per il seno dell’angolo che è l’angolo tra la
direzione del campo magnetico e la direzione della superficie.
Tenendo presente queste osservazioni si può dare la formula del momento che agisce su questa
spira:
M = F·br = (B·i·AB)·BC·sen = B·i·S·sen
( essendo S la superficie racchiusa dalla spira e togliendo quindi quella condizione, introdotta solo
per motivi didattici, che la
spira fosse rettangolare).
Questo fenomeno è alla
base di varie applicazioni
tecniche come gli strumenti
di misurazione (tachimetro,
amperometri…) e dei
motori elettrici.
Schema per un motore elettrico a corrente continua:
Schema di un amperometro












