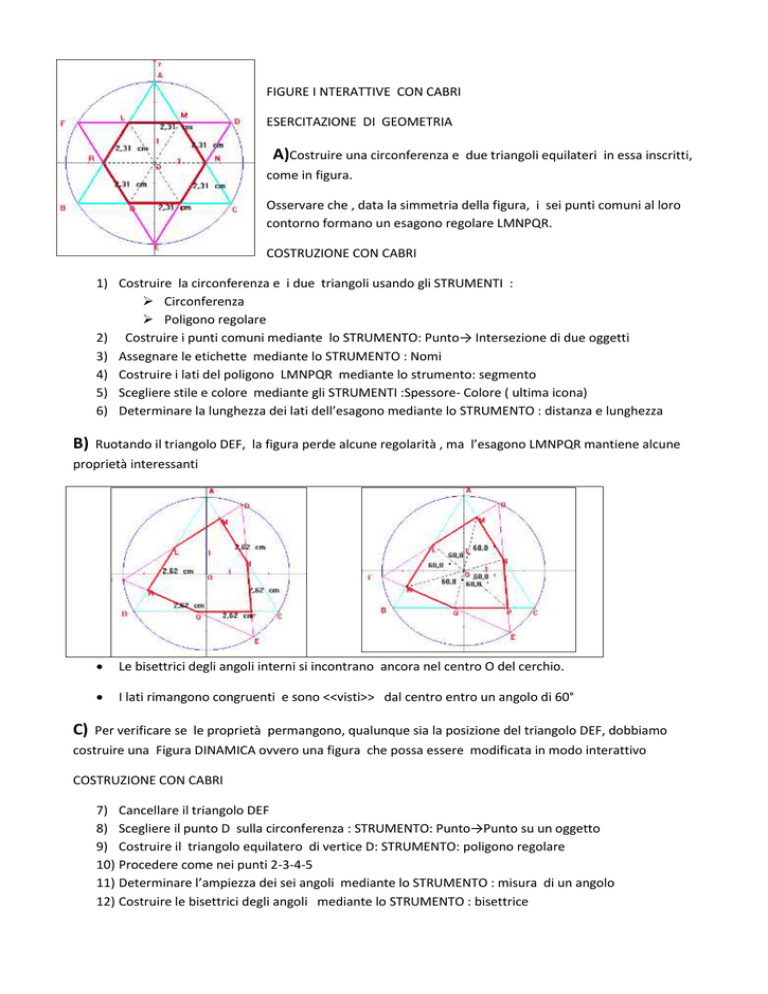
FIGURE I NTERATTIVE CON CABRI
ESERCITAZIONE DI GEOMETRIA
A)Costruire una circonferenza e
due triangoli equilateri in essa inscritti,
come in figura.
Osservare che , data la simmetria della figura, i sei punti comuni al loro
contorno formano un esagono regolare LMNPQR.
COSTRUZIONE CON CABRI
1) Costruire la circonferenza e i due triangoli usando gli STRUMENTI :
Circonferenza
Poligono regolare
2) Costruire i punti comuni mediante lo STRUMENTO: Punto→ Intersezione di due oggetti
3) Assegnare le etichette mediante lo STRUMENTO : Nomi
4) Costruire i lati del poligono LMNPQR mediante lo strumento: segmento
5) Scegliere stile e colore mediante gli STRUMENTI :Spessore- Colore ( ultima icona)
6) Determinare la lunghezza dei lati dell’esagono mediante lo STRUMENTO : distanza e lunghezza
B)
Ruotando il triangolo DEF, la figura perde alcune regolarità , ma l’esagono LMNPQR mantiene alcune
proprietà interessanti
C)
Le bisettrici degli angoli interni si incontrano ancora nel centro O del cerchio.
I lati rimangono congruenti e sono <<visti>> dal centro entro un angolo di 60°
Per verificare se le proprietà permangono, qualunque sia la posizione del triangolo DEF, dobbiamo
costruire una Figura DINAMICA ovvero una figura che possa essere modificata in modo interattivo
COSTRUZIONE CON CABRI
7) Cancellare il triangolo DEF
8) Scegliere il punto D sulla circonferenza : STRUMENTO: Punto→Punto su un oggetto
9) Costruire il triangolo equilatero di vertice D: STRUMENTO: poligono regolare
10) Procedere come nei punti 2-3-4-5
11) Determinare l’ampiezza dei sei angoli mediante lo STRUMENTO : misura di un angolo
12) Costruire le bisettrici degli angoli mediante lo STRUMENTO : bisettrice
13) Selezionare il punto D mediante il puntatore e
trascinarlo lungo la circonferenza
14) Osservare le figure ottenute e le misure evidenziate
D)
Dalla congettura alla dimostrazione:
a) Le rette OL,OM, ON, OP, OQ, OR sono bisettrici degli
angoli interni dell’esagono
Ricordiamo che la bisettrice di un angolo è il luogo dei punti
equidistanti dai due lati
Consideriamo per es. l’angolo di vertice L.
I lati LM ed LR appartengono a due corde di uguale
lunghezza
Corde di uguale lunghezza sono equidistanti dal centro O della circonferenza
Quindi…………………………………………………………………………………………………………………………………………………….
b)Congruenza dei lati :
Osservare i triangoli ALM- DMN - CNP - EPQ - BPR - FRL e verificare che sono tutti tra loro congruenti
-
Conviene concentrarsi su due di essi , per es. ALM e DMN
-
Essi hanno:
gli angoli ordinatamente uguali perché ……………………………………………………………………………………………..
i lati AM e DM uguali fra loro perché
………………………………………………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………………………………..quindi
sono tra loro congruenti per il ….……………………criterio di congruenza dei triangoli
In modo analogo si dimostra la congruenza delle altre coppie di triangoli aventi in comune un vertice
dell’esagono.
Si deduce che i lati dell’esagono LMNPQR sono tra loro congruenti
c) Ampiezza degli angoli al centro
Concentriamo l’attenzione sull’angolo
e sui due segmenti AE e DE., le cui rette formano gli angoli
E A ALM M B B E: Indichiamo con 2α l’ampiezza del primo di essi .
Il valore di α può essere espresso in funzione dell’angolo
A D = 2 A D, che individua la posizione del punto D.
……………………………………………………………………………………………………………...Dal Teorema dell’angolo esterno di
un triangolo si deduce che
M A =……………………………….
=……………………………………
Essendo OM e OL bisettrici degli angoli …………………………………………………………………………………………………….
………………………………………………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………………………………………………
………………………………………………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………………………………………..
E quindi
ha ampiezza 60° , qualunque sia la posizione del punto D












