ESERCIZI
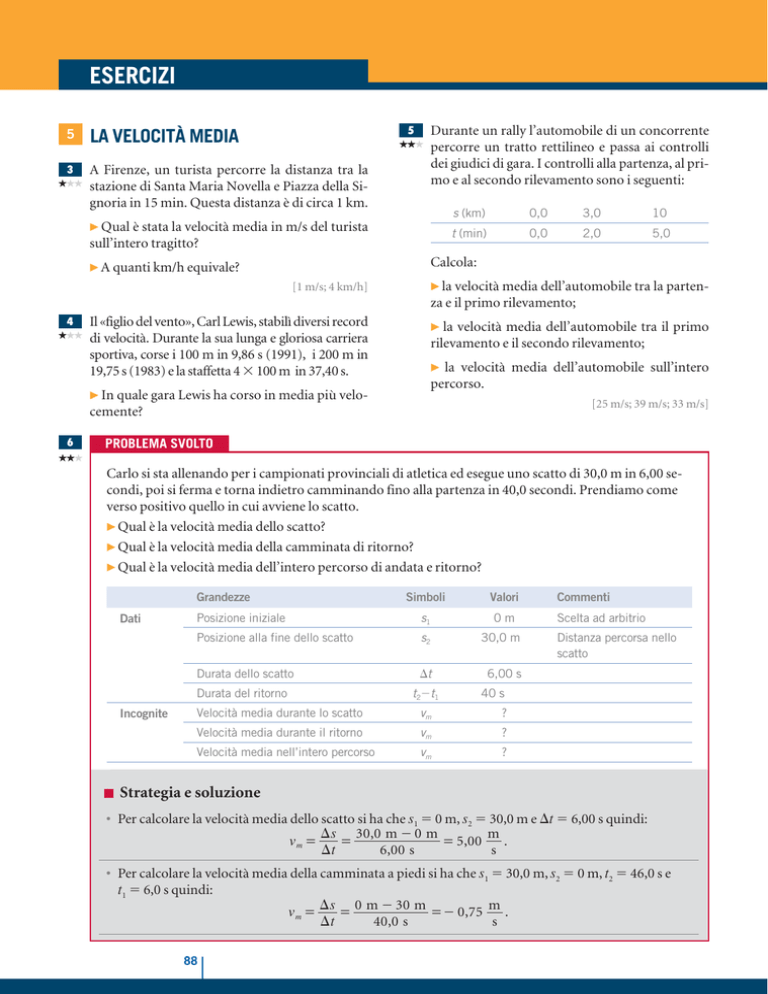
Durante un rally l’automobile di un concorrente
percorre un tratto rettilineo e passa ai controlli
dei giudici di gara. I controlli alla partenza, al primo e al secondo rilevamento sono i seguenti:
5
5
LA VELOCITÀ MEDIA
3
A Firenze, un turista percorre la distanza tra la
stazione di Santa Maria Novella e Piazza della Signoria in 15 min. Questa distanza è di circa 1 km.
Qual è stata la velocità media in m/s del turista
sull’intero tragitto?
s (km)
0,0
3,0
10
t (min)
0,0
2,0
5,0
Calcola:
A quanti km/h equivale?
la velocità media dell’automobile tra la parten-
[1 m/s; 4 km/h]
za e il primo rilevamento;
4
Il «figlio del vento», Carl Lewis, stabilì diversi record
di velocità. Durante la sua lunga e gloriosa carriera
sportiva, corse i 100 m in 9,86 s (1991), i 200 m in
19,75 s (1983) e la staffetta 4 100 m in 37,40 s.
la velocità media dell’automobile tra il primo
rilevamento e il secondo rilevamento;
la velocità media dell’automobile sull’intero
percorso.
In quale gara Lewis ha corso in media più velocemente?
6
[25 m/s; 39 m/s; 33 m/s]
PROBLEMA SVOLTO
Carlo si sta allenando per i campionati provinciali di atletica ed esegue uno scatto di 30,0 m in 6,00 secondi, poi si ferma e torna indietro camminando fino alla partenza in 40,0 secondi. Prendiamo come
verso positivo quello in cui avviene lo scatto.
Qual è la velocità media dello scatto?
Qual è la velocità media della camminata di ritorno?
Qual è la velocità media dell’intero percorso di andata e ritorno?
Grandezze
Dati
Incognite
Simboli
Valori
Posizione iniziale
s1
0m
Posizione alla fine dello scatto
s2
30,0 m
Durata dello scatto
t
6,00 s
Durata del ritorno
t2t1
Commenti
Scelta ad arbitrio
Distanza percorsa nello
scatto
40 s
Velocità media durante lo scatto
vm
?
Velocità media durante il ritorno
vm
?
Velocità media nell’intero percorso
vm
?
Strategia e soluzione
• Per calcolare la velocità media dello scatto si ha che s1 0 m, s2 30,0 m e t 6,00 s quindi:
m
s 30,0 m - 0 m
.
vm =
=
= 5,00
6,00 s
s
t
• Per calcolare la velocità media della camminata a piedi si ha che s1 30,0 m, s2 0 m, t2 46,0 s e
t1 6,0 s quindi:
m
s 0 m - 30 m
vm =
.
=
=- 0,75
40,0 s
s
t
88
• Per l’intero percorso si ha che s1 s2 0 e t 46,0 s, quindi:
0m
m
s
.
vm =
=
=0
s
t 46,0 s
Discussione
Il segno della velocità nelle prime due domande dà informazioni sul verso in cui Carlo si sta muovendo, positivo verso destra e negativo verso sinistra. Nella terza domanda lo spostamento complessivo è zero, quindi anche la velocità media calcolata sull’intero percorso è zero.
7
dell’acqua con un piede.
Uno yo-yo impiega 1,5 s a scendere di 75 cm e 1,8 s
per salire di 60 cm. Considera positivo il verso in
cui avviene la salita.
Calcola la velocità media:
nel tratto in discesa;
Stima l’intervallo di tempo nel quale l’impulso generato dal contatto con l’acqua raggiunge il
tuo cervello.
11
nel tratto in salita;
su tutto il percorso.
[ 0,50 m/s; 0,33 m/s; 0,045 m/s]
8
Una formica sta salendo lungo lo stelo di un fiore. Percorre 5,0 cm in 3,1 s, poi, spaventata da
un’ape che vola intorno alla corolla del fiore, si
ferma e scende lungo lo stesso stelo. Questa volta,
percorre la stessa distanza in 2,5 s. Considera positivo il verso in cui avviene la salita lungo lo stelo.
Quanto vale la velocità media in salita?
Quanti kilometri dista dalla Terra la stella Proxima Centauri?
[4,00 1013 km]
12
Quanto tempo impiega il gruppo di uccelli a
percorrere 1000 km?
Quanto vale la velocità media dell’intero percorso di salita e discesa?
[1,7 km/h; 0,46 m/s; 25 giorni]
9
Due amici, che programmano una vacanza in bicicletta, partono da Roma e fanno l’ipotesi di
mantenere una media di 20 km/h.
Quanti kilometri percorrerebbero in 8,0 ore?
Quanti giorni ci vorrebbero per arrivare a Milano, che dista 575 km, pedalando senza fermarsi?
[1,6 102 km; 1 d 4 h 45 min]
10
Nel corpo umano gli impulsi nervosi viaggiano a
una velocità media di circa 102 m/s. In piscina,
prima di immergerti, provi la temperatura
P.R. Bali
[0,016 m/s; 0,020 m/s; 0 m/s]
CALCOLO DELLA DISTANZA
E DEL TEMPO
Il fronte di migrazione di un gruppo di uccelli
migratori procede a una velocità media pari a circa 40 km al giorno.
Quanto vale la velocità media del fronte di migrazione in km/h e in m/s?
Quanto vale la velocità media in discesa?
6
La velocità della luce nel vuoto vale circa 300 000
km/s. Proxima Centauri, la stella più vicina a noi
dopo il Sole, dista dalla Terra 4,22 a.l., dove un anno luce è la distanza percorsa dalla luce in un anno.
13
Il rintocco di una campana lontana 1 km indica
che è mezzogiorno in punto.
In realtà quando sento il suono che ore sono?
(Suggerimento: per la velocità del suono, usa il valore 3,32 102 m/s)
[Mezzogiorno e 3 secondi]
89
ESERCIZI
7
Calcola la velocità media nei quattro tratti.
IL GRAFICO SPAZIO-TEMPO
Calcola la velocità media sull’intero percorso.
14
Disegna il grafico spazio-tempo di una tartaruga
che:
parte dalla posizione 0 m all’istante 0 s;
[50 km/h; 25 km/h; 0 km/h; 75 km/h; 36,8 km/h]
17
Il grafico rappresenta il moto di un ragazzo.
si muove alla velocità di 0,5 cm/s per 2 secondi;
200
si ferma per un secondo;
180
riparte alla velocità di 0,2 cm/s per 4 secondi.
160
140
Il grafico rappresenta il moto di un’automobile.
s (m)
15
120
100
80
180
60
160
40
140
20
s (km)
120
0
100
0
20
40
80
60
80
100
120
t (s)
60
40
Descrivi come varia la velocità.
20
Calcola la velocità media sull’intero tragitto.
0
0
0,5
1,0
1,5
2,0
2,5
3,0
3,5
Quale distanza percorre?
t (h)
[1,6 m/s; 160 m]
In quale tratto l’automobile è ferma?
Per quanto tempo resta ferma?
18
In quale tratto la velocità è maggiore?
Disegna il grafico spazio-tempo del moto di una
bicicletta a partire dalla tabella.
Che valore ha la velocità massima?
t (h)
s (km)
A
0,00
0,00
B
0,20
14,00
Cosa accade nell’ultimo tratto?
Quanto vale la velocità media nell’ultimo tratto?
16
Il grafico rappresenta il moto di un motorino.
C
0,50
18,00
D
0,70
18,00
E
1,00
12,00
In quale tratto la velocità è più grande?
s (km)
tratto
tratto
Che cosa succede nel tratto CD?
tratto tratto
150
E nel tratto DE?
100
Quanto vale la velocità media nel tratto DE?
50
t (h)
1
90
2
3
4
[20 km/h]
8
DAL GRAFICO SPAZIO-TEMPO
AL MOTO
tafoglio a casa. Quindi cambia verso lungo la
stessa traiettoria rettilinea e raggiunge di nuovo
l’origine all’istante t 14 s.
19
Considera il grafico spazio-tempo disegnato qui
sotto.
Disegna il grafico spazio-tempo del moto di
Luigi.
Calcola la velocità media di Luigi sull’intero
percorso.
[0 m/s]
Descrivi il moto rappresentato dal grafico nei
successivi intervalli di tempo.
Calcola la velocità media in ognuno dei tratti
indicati.
9
IL MOTO RETTILINEO UNIFORME
22
I due segmenti rappresentano il moto di due automobili che si muovono di moto rettilineo uniforme.
s (m)
400
300
200
7,0
A
6,0
100
B
1
2
3
4
5
s (km)
5,0
6
t
(s)
4,0
3,0
2,0
20
Considera il grafico spazio-tempo disegnato qui
sotto.
1,0
0
0
Descrivi il moto rappresentato dal grafico nei
successivi intervalli di tempo.
1,0
2,0
3,0
4,0
t (min)
Calcola la velocità delle due automobili.
Calcola la velocità media in ognuno dei tratti
indicati.
Che cosa succede nel punto di intersezione delle due rette?
5
[25 m/s; 8,3 m/s]
4
23
s (m)
3
2
1
t
0
2
4
6
8
10
–1
–2
t (s)
21
La tabella si riferisce a un podista che corre sul
rettilineo del lungomare.
Luigi parte all’istante t 0 s da casa propria, presa come origine s 0 m, e si sposta lungo una
traiettoria rettilinea di 2 m in 3 s. Poi si ferma al
semaforo per 5 s; in seguito si sposta di altri 4 m
in 4 s finché si accorge di aver dimenticato il por-
s
t2 t1 150 s
s2 s1 500 m
t3 t2 225 s
s3 s2 749 m
t4 t3 150 s
s4 s3 350 m
t5 t4 750 s
s5 s4 2498 m
s/t
Completa la tabella.
Disegna il grafico spazio-tempo nell’ipotesi
che all’istante 0 s il podista si trovi nella posizione
0 m.
91
ESERCIZI
4500
10
CALCOLO DELLA POSIZIONE E DEL
TEMPO NEL MOTO UNIFORME
26
La Luna dista dalla Terra 3,8 108 m. La luce viaggia
nel vuoto con velocità costante pari a 300 000 km/s.
4000
3500
s (m)
3000
2500
2000
In quanti secondi un segnale luminoso arriva
dalla Terra alla Luna?
1500
1000
[1,3 s]
500
0
0
27
1000
500
t (s)
Il podista si muove di moto rettilineo uniforme?
Un fulmine cade a 1 km di distanza. La luce e il suono viaggiano di moto rettilineo uniforme alle velocità rispettivamente di 300 000 km/s e 332 m/s.
Quanto tempo passa prima di vedere il lampo?
E prima di sentire il tuono?
24
Un’automobile si muove di moto rettilineo uniforme secondo la legge del moto s (20 m/s) t,
dove s è espresso in metri e t in secondi.
[3 106 s; 3 s]
28
Rappresenta il moto con un grafico spaziotempo.
Che distanza ha percorso l’automobile nell’intervallo di tempo da 10 s a 30 s?
Quale dei due amici arriva prima al cinema?
[4,0 102 m]
25
Uno studente si muove, in bicicletta, a velocità
costante. Il suo moto è rappresentato dal grafico
seguente.
Due amici escono di casa alla stessa ora e si dirigono
verso lo stesso cinema. Il primo abita a 1,6 km dal
luogo dell’appuntamento e va a piedi con una velocità di 6 km/h. Il secondo abita a 8,3 km e usa il motorino con una velocità di 50 km/h.
Quanto tempo deve aspettare prima che arrivi
l’altro?
[6 min]
29
Calcola la velocità con cui lo studente si muove
Scrivi l’equazione del suo moto.
Calcola la distanza percorsa dopo 20 s.
Alla maratona di New York, un atleta spagnolo
parte esattamente sotto lo striscione dello START
con velocità costante di 18,0 km/h, mentre un
atleta italiano parte 200 m più indietro con
velocità costante di 21,6 km/h.
Scrivi le leggi orarie dei due maratoneti.
[6,7 m/s, s (6,7 m/s) t; 1,3 102m]
Calcola dopo quanto tempo si incontrano.
s (m)
Determina quanta strada ha percorso l’italiano
dal momento della partenza fino all’istante in cui
raggiunge lo spagnolo.
300
[s (5,00 m/s) t; s (6,00 m/s) t 200 m; 200 s; 1,20 103 m]
200
30
100
Due fidanzati si corrono incontro con velocità costante partendo da una distanza di 30 m. La velocità
di Marco è 3,0 m/s mentre quella di Katia è 2,0 m/s.
Dopo quanto tempo si abbracciano?
10
20
92
30
40
50
t (s)
Che distanza ha percorso Katia?
[ 6,0 s; 12 m]
31
In un cartone animato un gatto scocca una freccia
per colpire un topo mentre questi cerca di raggiungere la sua tana che si trova a 5,0 m di distanza.
Il topo corre alla velocità di 20 km/h e la freccia a
33
Due ciclisti A e B percorrono la stessa strada dritta, partendo allo stesso istante. Dal grafico ricava:
s (km)
30 km/h. Inizialmente il gatto e il topo distano 10 m.
Disegna su una retta orientata le posizioni ini-
50
ziali del gatto e del topo e la posizione della tana.
40
Calcola il tempo che impiega il topo a raggiun-
30
gere la sua tana.
20
10
Calcola la distanza percorsa dalla freccia nello
stesso intervallo di tempo.
A
B
1
2
3
4
t (h)
Riesce a mettersi in salvo il topo?
[0,90 s; 7,5 m]
11
ESEMPI DI GRAFICI SPAZIO-TEMPO
32
I tre segmenti rappresentano il moto di tre automobili che si muovono di moto rettilineo uniforme.
Quale si riferisce al moto con velocità più alta?
Quale si riferisce al moto con velocità più bassa?
s (km)
la posizione iniziale di A e di B.
la loro velocità.
l’istante in cui sono nello stesso posto.
la posizione finale di ciascuno di essi.
Proponi un caso concreto che potrebbe essere
descritto dai due grafici.
Disegna in un diagramma v-t i grafici velocitàtempo dei due moti.
[0 km, 50 km; 13 km/h; 20 km/h; 1,5 h; 50 km; 0 km]
50
40
30
20
1
34
2
3
4
t (h)
PROBLEMA SVOLTO
Su una strada rettilinea si trovano due case A e B, che distano tra
loro 10 km.
Alice parte da B in motorino e si muove con velocità costante di
30 km/h verso destra.
Mezz’ora dopo, Clara esce dalla casa A in automobile e si muove
nella stessa direzione di Alice alla velocità costante di 80 km/h.
sincontro = ?
Vmoto = 30 km/h
55
0
5
10
50
15
45
40
35
30
B
A
20
25
d = 10 km
Vauto = 80 km/h
tincontro = ?
Dove si incontrano Alice e Clara?
Dopo quanto tempo?
55
0
40
35
5
10
50
A
15
45
30
20
25
93
B
ESERCIZI
Grandezze
Dati
Simboli
Valori
Distanza tra le case A e B
Velocità del motorino
10 km
30 km/h
Vmoto
Ritardo dell’automobile
Incognite
Commenti
1/2 ora
Velocità dell’auto
Vauto
80 km/h
Posizione dell’incontro
sincontro
?
Determinare graficamente
Istante di tempo dell’incontro
tincontro
?
Determinare graficamente
Strategia e soluzione
80
posizione (km)
70
Risolviamo il problema con l’ausilio del grafico spazio-tempo
del moto. Interpretiamo a parole il risultato ottenuto.
60
50
P
40
30
20
10
O
1
2
1
3
2
tempo (h)
• Indichiamo in blu il moto del motorino e in rosso quello dell’automobile. Poiché i due moti sono
entrambi rettilinei uniformi, nel grafico spazio-tempo essi sono rappresentati da due rette.
• Fissiamo in A l’origine dell’asse verticale delle posizioni. Allora, al tempo t0 0 Alice parte dalla
posizione iniziale s0 10 km. Dopo mezz’ora, cioè al tempo t 1/2 h, Clara parte in automobile
dal punto s 0 km.
• Al tempo t1 1 h, Alice che si muove alla velocità di 30 km/h avrà percorso 30 km e si troverà,
applicando la formula (6), nel punto s 10 km 30 km/h 1 h 40 km. Clara, che è partita
mezz’ora dopo e viaggia alla velocità di 80 km/h, avrà percorso invece 40 km, poiché nel moto
rettilineo uniforme le distanze sono direttamente proporzionali agli intervalli di tempo impiegati a
percorrerli.
• Osserviamo che i due veicoli si incontrano nello stesso istante di tempo e nella stessa posizione. Le
due rette si incontrano nel punto P, le cui coordinate ci dicono che dopo 1 h dalla partenza di Alice
in motorino, Clara la raggiunge in automobile a 40 km da A.
35
Due messaggeri A e B si devono incontrare per
scambiarsi delle lettere. Entrambi partono a cavallo a mezzogiorno dai loro castelli, collegati da
una strada rettilinea lunga 30 km. Il messaggero
A corre alla velocità costante di 17 km/h, il messaggero B di 13 km/h.
A che distanza dal castello di A si incontrano?
Dopo quanto tempo dalla partenza avviene
l’incontro?
94
Trova la soluzione anche per via grafica.
[17 km; 1,0 h]
36
Un autobus si muove su una strada rettilinea a
velocità costante pari a 36 km/h. All’istante iniziale passa per l’origine del sistema di riferimento
scelto. Gianni è fermo a una distanza di 100 m
dall’origine. Dopo 4,0 s vede l’autobus e gli corre
incontro con una velocità di 6,0 km/h.
Dopo quanto tempo da quando lo avvista
Gianni incontra l’autobus?
nerla a lungo. In una scena di caccia, la pantera e
l’antilope scattano contemporaneamente quando
la loro distanza è 15 m, e si muovono in linea retta.
Determina la posizione di Gianni nel momento in cui raggiunge l’autobus.
Traduci le velocità in m/s.
Disegna in un diagramma s-t i grafici spaziotempo dei due moti.
Rappresenta su una retta la posizione iniziale
della pantera (0 m) e quella dell’antilope.
Disegna in un diagramma v-t i grafici velocitàtempo dei due moti.
Scrivi la legge del moto della pantera.
[5,1 s; 91 m]
37
Achille e la tartaruga si sfidano in una gara di corsa su una traiettoria rettilinea a velocità costanti.
La tartaruga parte all’istante iniziale t 0 s con
una velocità di 10,0 cm/s e un vantaggio su Achille di 100 m. Dopo 20,0 s, Achille parte per raggiungerla e corre, nello stesso verso della tartaruga, con velocità pari a 8,00 m/s.
Scrivi la legge del moto dell’antilope.
Calcola quali posizioni occuperebbero dopo 20 s.
La pantera riesce a raggiungere l’antilope?
[27,8 m/s; 23,6 m/s; sp (27,8 m/s) t;
sa 15 m (23,6 m/s) t; sp 5,6 102 m;
sa 4,9 102 m; sì]
3
Dopo quanto tempo dall’inizio della gara
Achille raggiunge la tartaruga?
Quanto vale la distanza percorsa da Achille?
Quanto tempo impiega la locomotrice del secondo treno a raggiungere la locomotrice del primo?
Disegna in un diagramma s-t i grafici spaziotempo del moto di Achille e di quello della tartaruga e determina graficamente l’istante e la posizione in corrispondenza dei quali Achille sorpassa la tartaruga.
Disegna in un diagramma v-t i grafici velocitàtempo dei due moti.
Dopo quanto tempo la locomotrice del secondo treno raggiunge la coda del primo?
[42 min; dopo 22 s in meno]
4
[32,9 s; 103 m]
tero percorso?
Quanto varrebbe la velocità media del treno se
non facesse soste intermedie?
[1,4 102 km/h; 1,5 102 km/h]
2
A che distanza dal semaforo si trovano i due
veicoli quando avviene il sorpasso?
Un treno eurostar impiega 4 h e 30 min a percorrere la distanza tra Roma e Milano (632 km), con
una sosta a Bologna di 4,0 min e una sosta a Firenze di 8,0 min.
Quanto vale la velocità media del treno sull’in-
La pantera può tenere una velocità di 100 km/h
per circa 20 s, ma poi deve fermarsi.
L’antilope, invece, può raggiungere in corsa una
velocità massima di 85 km/h, ma riesce a mante-
Un’automobile attraversa un semaforo alla velocità di 72 km/h. Nello stesso istante, uno scooter
che si trova 1,5 km più avanti, mantiene una velocità di 36 km/h.
Quanto tempo impiega l’automobile a raggiungere lo scooter?
PROBLEMI GENERALI
1
Un treno lungo 150 m parte dalla stazione alle
15:05 e procede alla velocità di 70 km/h. Un secondo treno parte dalla stessa stazione alle 15:20 e procede alla velocità di 95 km/h sul binario parallelo.
[2,5 min; 3,0 km]
5
Il grafico rappresenta la posizione di una formica
che si sta muovendo lungo il tronco di un albero.
s (cm)
4
3
2
1
0
-1
-2
1 2 3 4
t (s)
95