CAMPO MAGNETICO ROTANTE

Università degli studi di Pisa
FACOLTÀ DI INGEGNERIA
Corso di Laurea Triennale in Ingegneria Elettrica
DISPENSE DI MACCHINE ELETTRICHE
TRATTE DAL CORSO TENUTO DAL PROF.
OTTORINO BRUNO
CAMPO MAGNETICO
ROTANTE
A cura dello studente Gabriele Giovanni Padovano
Con la supervisione del prof. Luca Sani
Anno Accademico 2011/12
Indice
Indice delle figure
1
1 Campo magnetico rotante
1.1 Distribuzione di f.m.m prodotta da una bobina diametrale . .
1.2 Scomposizione del campo magnetico rotante . . . . . . . . . .
1.3 Campo magnetico al traferro generato da un avvolgimento
trifase alimentato in corrente alternata . . . . . . . . . . . . .
1
2
5
i
7
Elenco delle figure
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
Statore di un motore asincrono trifase. . . . . . . . . . . . . .
Andamento dell’onda di campo nel traferro e della prima
armonica. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Rappresentazione del campo sinusoidale pulsante al traferro. .
Scomposizione del campo magnetico rotante in due campi
contro-rotanti. . . . . . . . . . . . . . . . . . . . . . . . . . .
Andamento della prima componente del campo magnetico
rotante. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Andamento della seconda componente del campo magnetico
rotante. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Avvolgimento di statore. . . . . . . . . . . . . . . . . . . . . .
Andamento nel tempo della scomposizione in armoniche del
campo magnetico rotante. . . . . . . . . . . . . . . . . . . . .
ii
2
3
4
5
6
6
7
10
Capitolo 1
Campo magnetico rotante
In questa parte della dispensa si procedere allo studio del campo magnetico
rotante. In particolare, si vuole illustrare come sia possibile scambiare una
coppia tra due strutture coassiali. Questo aspetto è la base della conversione
elettromeccanica dell’energia che si attua nelle macchine rotanti in alternata.
Nel corso della trattazione saranno considerate valide le seguenti ipotesi
semplificative:
ˆ le linee di campo entrano ed escono ortogonalmente rispetto alla struttura in ferro;
ˆ la macchina si comporta in modo lineare;
ˆ il fenomeno sia piano, ovvero si trascurano gli effetti di bordo.
ˆ si trascurano, dal punto di vista della conversione elettromeccanica dell’energia, gli effetti delle armoniche spaziali di f.m.m prodotte
dagli avvolgimenti reali. In altre parole, tale studio considera solo le
armoniche fondamentali delle distribuzioni spaziali al traferro;
ˆ i fenomeni di saturazione, isteresi e correnti parassite sono trascurati,
permettendo, cosı̀, di applicare il principio di sovrapposizione degli
effetti.
ˆ la caduta di tensione magnetica e presente solamente nel traferro δ,
quindi si considera la permeabilita magnetica del ferro infinita rispetto
a quella dell’aria (ossia µr >> µ0 e quindi <f erro = 0).
L’enunciato del teorema di Galileo Ferraris è il seguente:
Tre avvolgimenti con lo stesso numero di spire, disposti nello spazio a 23 π tra
loro e percorsi da una terna equilibrata di correnti alternate, con pulsazione
ω e sfasate tra loro nel tempo di 32 π, originano un campo magnetico rotante
con velocità ω e di ampiezza pari a 23 il campo massimo, prodotto da ogni
singolo avvolgimento.
1
CAMPO MAGNETICO ROTANTE
1.1
2
Distribuzione di f.m.m prodotta da una bobina diametrale
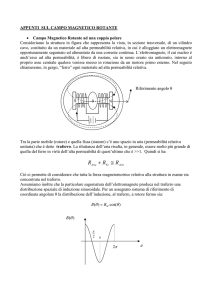
Si consideri la struttura elettromagnetica illustrata in figura rappresentante
una bobina di N1 spire in serie. I conduttori di andata (a sinistra, percorsi da corrente uscente dal piano della figura) ed i conduttori di ritorno
(a destra, percorsi da corrente entrante dal piano della figura) della bobina
siano collocati in posizione diametrale e percorsi dalla corrente I, che per il
momento si considera una corrente continua fittizia con il solo compito di
evidenziare la distribuzione di f.m.m..
Data la simmetria della struttura, si può ritenere che le linee di campo magnetico, prodotte dalla bobina, abbiano l’andamento qualitativo illustrato
in figura col tratteggio.
Secondo la legge della circuitazione magnetica di Ampere, la f.m.m. concatenata da ciascuna linea di campo vale:
Z
NI
H · dl = N I → 2Hδ = N I → H =
(1.1)
2δ
Γ
Figura 1.1: Statore di un motore asincrono trifase.
Tale f.m.m. serve a compensare la caduta di tensione magnetica nei due attraversamenti di traferro relativi ad ogni linea di campo. Pertanto, tenendo
conto del verso delle linee di campo, la distribuzione di caduta di tensione
magnetica lungo la circonferenza di traferro (detta distribuzione di f.m.m.
al traferro) assume una forma ad onda quadra.
La funzione descritta nella fig.1.2 è una funzione periodica e alternativa,
quindi scomponibile in serie di Fourier. Nello sviluppo della serie, tutte le
CAMPO MAGNETICO ROTANTE
3
Figura 1.2: Andamento dell’onda di campo nel traferro e della prima
armonica.
armoniche di ordine pari, e tutti i termini in seno, non sono presenti essendo
h(θ) una funzione pari.
La funzione può essere espressa come:
∞
X
hn (θ) =
n=1,3,5...
4 · AM
cos θ
nπ
(1.2)
essendo AM = N2δI , la precedente relazione diventa:
hn (θ) =
2N I
cos θ
nδπ
(1.3)
Ai fini dello studio semplificato del campo magnetico rotante assume particolare rilevanza l’armonica fondamentale della distribuzione di f.m.m. che
si ottiene ponendo n=1:
h1 =
2N I
cos θ = KI cos θ
nδπ
(1.4)
da cui si evince che l’onda di campo magnetico risulta funzione della corrente I e della coordinata angolare θ.
Supponiamo, ora, di inviare nell’avvolgimento una corrente non più continua, ma sinusoidale del tipo: i(t) = IM sin ωt.
La distribuzione spaziale di campo al traferro prodotta dalla corrente non
rimane, quindi, fissa nello spazio ad ogni istante di tempo, ma verrà a dipendere, istante per istante, dal valore della corrente, oscillando tra un valore
i
−N i
massimo ( N
2δ ) e un valore minimo ( 2δ ).
In tal caso:
h1 (θ, t) =
2N IM sin ωt
cos θ
δπ
(1.5)
CAMPO MAGNETICO ROTANTE
4
Figura 1.3: Rappresentazione del campo sinusoidale pulsante al traferro.
Usando, poi, le formule di prostaferesi
1
sinα · cosβ = [sin(α − β) + sin(α + β)]
2
la (1.5) diventa:
1
h1 = HM sin(ωt − θ) + sin(ωt + θ)
2
dove HM = 2NδπIM .
(1.6)
CAMPO MAGNETICO ROTANTE
1.2
5
Scomposizione del campo magnetico rotante
La precedente relazione permette di scrivere il campo pulsante al traferro
come la somma di due funzioni che dipendono dal tempo e dallo spazio. Tali
funzioni sono delle onde, cioè delle sinusoidi di ampiezza costante.
Il teorema di Galileo Ferraris, infatti, afferma che: un campo magnetico con
distribuzione sinusoidale fissa nello spazio e pulsante sinusoidalmente nel
tempo può essere scomposto in due onde controrotanti (diretta e invers) di
campo magnetico non alternative, con velocità ω e di ampiezza costante nel
tempo pari a metà del campo alternativo totale.
Figura 1.4: Scomposizione del campo magnetico rotante in due campi
contro-rotanti.
La prima componente del campo, quella diretta, è:
1
hd (θ) = HM sin(ωt − θ)
2
(1.7)
Fissato il tempo t, è possibile tracciare l’andamento di hd in funzione di θ:
1. per t=0 → hd = 12 HM sin(−θ) (curva blu);
2. per il generico t* tale per cui ωt∗ − θ∗ = 0 (curva rossa).
Dalla figura si deduce che hd è una sinusoide che trasla lungo il traferro con
velocità θ̇ = ω.
CAMPO MAGNETICO ROTANTE
6
Figura 1.5: Andamento della prima componente del campo magnetico
rotante.
La seconda componente del campo, quella inversa, è:
1
hd (θ) = HM sin(ωt + θ)
2
(1.8)
Fissato il tempo t, è possibile tracciare l’andamento di hi in funzione di θ:
1. per t=0 → hi = 12 HM sin(θ); (curva blu)
2. per il generico t* tale per cui ωt∗ + θ∗ = 0 (curva rossa).
Dalla figura si deduce che hi è una sinusoide che trasla lungo il traferro con
velocità θ̇ = −ω.
Figura 1.6: Andamento della seconda componente del campo magnetico
rotante.
CAMPO MAGNETICO ROTANTE
1.3
7
Campo magnetico al traferro generato da un
avvolgimento trifase alimentato in corrente alternata
Nelle macchine elettriche l’avvolgimento disposto sullo statore è nella grande
maggioranza dei casi un avvolgimento trifase.
Si supponga l’avvolgimento trifase formato da tre avvolgimenti monofase
identici tra loro e sfasati di 120° elettrici, come mostrato nella seguente
figura.
Figura 1.7: Avvolgimento di statore.
Le tre fasi siano percorse da una terna equilibrata di correnti sinusoidali,
tale che:

i1 (t) = IM sin ωt
i2 (t) = IM sin ωt − 32 π (1.9)

i1 (t) = IM sin ωt + 32 π
Per il generico avvolgimento di fase di ordine i, il campo avrà la seguente
espressione:
∞
X
2
hi (θ) =
HM cos(nθ − i π + αn )
(1.10)
3
n=1
Quindi si ha:

P
h1 (θ) = ∞

n=1 Hn cos(nθ + αn )




P
h2 (θ) = ∞
Hn cos nθ − 32 π + αn
n=1




P

2
h3 (θ) = ∞
n=1 Hn cos nθ + 3 π + αn
(1.11)
CAMPO MAGNETICO ROTANTE
8
I
Sapendo che HM = 2N
δπn e sostituendo le espressioni delle correnti, il precedente sistema diventa:

P∞
h
(θ,
t)
=

1
n=1 HM n sin ωt cos(nθ + αn )




P
HM n sin ωt − 23 π cos nθ − 23 π + αn
h2 (θ, t) = ∞
(1.12)
n=1




P

h3 (θ, t) = n = 1∞ HM n sin ωt + 23 π cos nθ + 23 π + αn
Applicando le formule di prostaferesi e considerando l’ipotesi di linearità della macchina, il campo magnetico risultante limitato alla sola prima armonica
hσ1 (θ, t) è dato dalla somma dei singoli campi di ogni fase, ovvero:
h
1
hσ1 (θ, t) = HM sin(ωt − θ − α1 ) + sin(ωt + θ + α1 )+
2
2
2
2
+ sin ωt − π − θ + π − α1 + sin(ωt − π + θ −
3
3
3
2
2
2
+ sin ωt + π − θ − π − α1 + sin(ωt + π + θ +
3
3
3
2
π + α1 +
3
i
2
π + α1
3
(1.13)
Operando le opportune semplificazioni si ottiene:
h
1
4
hσ1 (θ, t) = HM 3 sin(ωt − θ − α1 ) + sin(ωt + θ + α1 ) + sin ωt + θ − π + α1 +
2
3
|
{z
}
i
4
+ sin ωt + θ + π + α1
|
{z 3
}
(1.14)
Poichè i termini evidenziati costituiscono una terna simmetrica di vettori la
cui somma istante per istante è pari a 0, il campo complessivo approssimato
alla prima armonica assume la seguente forma:
3
hσ1 (θ, t) = HM sin(ωt − θ − α1 )
2
(1.15)
Abbiamo dimostrato che se alimentiamo i tre avvolgimenti di statore con
una sequenza diretta di correnti si ottiene la componente diretta di campo
che si muove con velocità θ̇ = ω.
Qualora si alimentassero i tre avvolgimenti di statore con una sequenza inversa di correnti invertendo tra loro le correnti delle fasi 2 e 3, si otterrebbe
la componente inversa che si muove con velocità θ̇ = −ω.
Vediamo, ora, la forma assunta dal campo magnetico rotante per l’n-esima
CAMPO MAGNETICO ROTANTE
9
armonica:
h
1
hσn (θ, t) = HM n sin(ωt − nθ − αn ) + sin(ωt + nθ + αn )+
2
2
2
2
2
+ sin ωt − π − nθ + n π − αn + sin(ωt − π + nθ − n π + αn +
3
3
3
3
i
2
2
2
2
+ sin ωt + π − nθ − n π − αn + sin(ωt + π + nθ + n π + αn
3
3
3
3
(1.16)
Raccogliendo e semplificando, si ha:
h
1
hσn (θ, t) = HM n sin(ωt − nθ − αn ) + sin(ωt + nθ + αn )+
2
2
2
+ sin ωt − nθ + (n − 1) π − αn + sin(ωt + nθ − (n + 1) π + αn +
3
3
i
2
2
+ sin ωt − nθ − (n − 1) π − αn + sin(ωt + nθ + (n + 1) π + αn
3
3
(1.17)
E’ possibile distinguere tre gruppi di armoniche:
1. primo gruppo tale per cui n=3k;
2. secondo gruppo tale per cui n=3k+1;
3. terzo gruppo tale per cui n=3k+2.
Sia k=1,2,3..., allora si ha:
ˆ ARMONICHE DEL PRIMO GRUPPO: sono tutte quelle multiple di
3 (3,6,9...); ponendo k=1 si ottiene n=3. Sostituendo nella (1.17)
il valore n=3, si ottengono due terne simmetriche ed equilibrate di
vettori, la cui somma è nulla.
Quindi tutte le armoniche del 1°gruppo, hanno come campo risultante
un campo nullo per ogni valore di k.
ˆ ARMONICHE DEL SECONDO GRUPPO: sono la 4,7,13...; ponendo
k=1 si ottiene n=4. Questa armonica non è presente essendo pari;
quindi si pone k=2 e si ha n=7. Sostituendo nella (1.17) il valore n=7
si ha:
h
1
hσ7 (θ, t) = HM 7 sin(ωt − 7θ − α7 ) + sin(ωt + 7θ + α7 )+
2
2
2
+ sin ωt − 7θ + (7 − 1) π − α7 + sin(ωt + 7θ − (7 + 1) π + α7 +
3
3
i
2
2
+ sin ωt − 7θ − (7 − 1) π − α7 + sin(ωt + 7θ + (7 + 1) π + α7
3
3
(1.18)
CAMPO MAGNETICO ROTANTE
10
Operando le opportune semplificazioni si ottiene:
3
hσ7 (θ, t) = HM 7 sin(ωt − 7θ − α7 )
2
con HM 7 =
(1.19)
2N IM
7δπ
ˆ ARMONICHE DEL TERZO GRUPPO: sono la 5,8,11...; ponendo
k=1 si ottiene n=5. Sostituendo nella (1.17) il valore n=5 si ha:
h
1
hσ5 (θ, t) = HM 5 sin(ωt − 5θ − α5 ) + sin(ωt + 5θ + α5 )+
2
2
2
+ sin ωt − 5θ + (5 − 1) π − α5 + sin(ωt + 5θ − (5 + 1) π + α5 +
3
3
i
2
2
+ sin ωt − 5θ − (5 − 1) π − α5 + sin(ωt + 5θ + (5 + 1) π + α5
3
3
(1.20)
Operando le opportune semplificazioni si ottiene:
3
hσ5 (θ, t) = HM 5 sin(ωt + 5θ − α5 )
2
con HM 5 =
(1.21)
2N IM
5δπ
Nella seguente figura si riporta l’andamento della fondamentale, della quinta
e della settima armonica.
Figura 1.8: Andamento nel tempo della scomposizione in armoniche del
campo magnetico rotante.
Dal grafico si deduce che:
CAMPO MAGNETICO ROTANTE
11
ˆ l’armonica fondamentale, si annulla per un istante generico t∗ tale che
ωt∗ − θ − α1 = 0 → t∗ =
θ + α1
ω
ˆ la settima armonica ha un’ampiezza pari a
ruota nello stesso verso con velocità θ̇ = ω7 ;
1
7
ˆ la quinta armonica ha un’ampiezza pari a
ruota in verso opposto con velocità θ̇ = ω5 .
della fondamentale, ma
1
5
della fondamentale e