Unità
Le
1
frazioni e i numeri decimali
GLI ESERCIZI
1 Indica, segnando con una crocetta, quali delle seguenti divisioni hanno il quoziente nell’insieme
N e quali nell’insieme Q+:
N Q+
N Q+
3
__
✗
3 : 8 = .........
✗
8
9
__
✗
9 : 11 = .........
✗
11
26
✗
26 : 32 = .........
✗
__
32
9 ✗
✗
72 : 8 = .........
8
8 : 10 = ___
10
9 54 : 6 = .........
7 49 : 7 = .........
6
__
6 : 9 = .........
9
2 Completa la tabella inserendo in modo corretto i seguenti numeri:
__
19,330,
5
__
1024,0
6
Numero naturale
16
432
Numero decimale
limitato
16
19,3
__
17,413
__
51,8
__
15,7
174,3
4150,3
54,632
___
Numero decimale illimitato
periodico semplice
periodico misto
30,517,413
10
174,3
15,7
24,06
432
4150,3
51,8
54,632
Giochiamo insieme
Un tronco d’albero è stato tagliato a fette per fini scientifici. Qual è la frazione che manca?
soluzioni a pag. 138
3
Unità
Le
1
frazioni e i numeri decimali
GLI ESERCIZI
1 Stabilisci, senza eseguire il calcolo, se le seguenti frazioni generano un numero naturale, decimale limitato o decimale illimitato (periodico semplice o misto):
6
___
20
...................................................................................................................................................................................................
14
___
decimale illimitato (p. semplice)
...................................................................................................................................................................................................
6
decimale limitato
18
____
decimale limitato
...................................................................................................................................................................................................
100
16
___
decimale illimitato (p. semplice)
...................................................................................................................................................................................................
26
___
decimale illimitato (p. misto)
...................................................................................................................................................................................................
34
___
decimale illimitato (p. misto)
...................................................................................................................................................................................................
8
___
decimale illimitato (p. misto)
...................................................................................................................................................................................................
54
44
24
90
74
____
decimale illimitato (p. misto)
...................................................................................................................................................................................................
108
22
____
decimale illimitato (p. misto)
...................................................................................................................................................................................................
120
7
___
25
decimale limitato
...................................................................................................................................................................................................
2 Completa la tabella indicando il periodo e l’antiperiodo dei seguenti numeri decimali periodici:
Numero
__
14,5
__
26,08
___
14,072
__
36,008
____
1210,24618
____
0,00563
____
216,23156
__
34,4
Periodo
Antiperiodo
5
–
8
0
72
0
8
00
618
24
563
00
156
23
4
–
5
generatrice
3 Frazione
di un numero decimale
LA TEORIA
Per trasformare un numero decimale limitato in una frazione, si scrive a numeratore il numero naturale che si ottiene togliendo la virgola (senza scrivere gli zeri) e a denominatore
si scrive 1 seguito da tanti zeri quante sono le cifre decimali del numero dato:
2643
43
2,643
= _____
0,43 = ____
100
1000
Per trasformare un numero decimale periodico semplice in una frazione, si scrive a numeratore la differenza fra tutto il numero dato, senza la virgola, e la sua parte intera e a
denominatore si scrivono tanti 9 quante sono le cifre del periodo:
___
_____
509
514 – 5
3215
= ____ 0,
3215
= _____
5,14 = ________
99
99
9999
Per trasformare un numero decimale periodico misto in una frazione, si scrive a numeratore la differenza fra tutto il numero dato, scritto senza la virgola, e tutta la parte che precede
il periodo, senza la virgola e a denominatore si scrivono tanti 9 quante sono le cifre del
periodo e tanti 0 quante sono le cifre dell’antiperiodo:
___
___
6437 – 64 _____
6373
32 =
=
0,08
6,437 = __________
990
990
832 – 8
824
________
= _____
9900
9900
GLI ESERCIZI
1 Trasforma in frazione i seguenti numeri decimali:
1534
5435
543,5 = ................................................................................
15,34 = ____
____
100
10
46
191 216
______
0,046 = ____
................................................................................
19,1216 = ...........................................................................
1000
10 000
2 Trasforma in frazione i seguenti numeri decimali periodici:
__
__
534 − 53
1113
1236 − 123 ____
481
___
123,
6 = .._________
..............................................................................
53,4 = ________ = .....................................................
=
=
9
9
9
9
___
___
1602
8758
8846
− 88 ____
1618 − 16 ____
_________
16,18 = .._________
...............................................................................
88,46 = ...............................................................................
=
=
99
99
99
99
3 Trasforma in frazione i seguenti numeri decimali periodici misti:
___
___
7315 − 73 ____
6172
6234
− 62 ____
_________
= 7242
................................................
6,234 = ................................................................................
7,315 = _________
=
990
990
990
990
__
___
29 307
32 563 − 3256 _____
61261 − 612 60 649
__________
32,563 = .............................................................................
83,261 = .............................................................................
___________
=
= _____
900
990
900
990
6
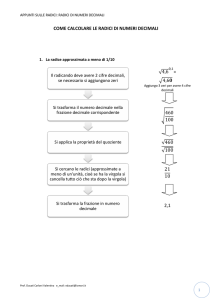
si approssima
4 Come
un numero decimale
Le
Unità
1
frazioni e i numeri decimali
LA TEORIA
Un numero decimale può avere molte cifre dopo la virgola e, nel caso di numeri periodici,
addirittura infinite. Per eseguire i calcoli con i numeri decimali è necessario tenere conto
solo di alcune cifre decimali. Si considerano quindi dei valori approssimati.
A seconda delle cifre considerate dopo la virgola si parla di approssimazione:
•ai decimali (0,1) se si considera la prima cifra dopo la virgola;
•ai centesimi (0,01) se si considerano le prime due cifre dopo la virgola;
•ai millesimi (0,001) se si considerano le prime tre cifre dopo la virgola.
Per approssimare correttamente un numero decimale è necessario verificare il valore della prima cifra trascurata:
• se questa ha valore minore o uguale a 5 ci si ferma alla cifra dei decimali voluta senza
modificarla;
• se questa ha valore maggiore di 5 si aumenta di una unità la cifra dei decimali cui ci si
ferma.
Nel primo caso si parla di approssimazione per difetto, nel secondo di approssimazione per eccesso. Per esempio, se si vuole approssimare ai decimi il numero
5,328 si scrive: 0,1
5,3
5,328 approssimazione per difetto perché la
prima cifra trascurata (2) è minore di
5 e non si modifica nulla
cifra < 5
Se si vuole approssimare ai centesimi il numero 7,348 si scrive:
7,348 0,01
7,35
cifra > 5
approssimazione per eccesso perché
la prima cifra trascurata (8) è maggiore di 5 e si aggiunge 1 unità alla cifra
dei centesimi (in questo caso)
GLI ESERCIZI
1 Completa la tabella approssimando ai decimi i seguenti numeri decimali e indica con una crocetta il tipo di approssimazione:
Numero
Approssimazione
ai decimi
Approssimazione
per difetto
Approssimazione
per eccesso
6,748
22,396
6,7
22,4
✗
✗
16,278
16,3
✗
126,326
126,3
✗
7
4 Come si approssima un numero decimale
2 Completa la tabella approssimando ai centesimi i seguenti numeri decimali e indica con una
crocetta il tipo di approssimazione:
Numero
11,2852
Approssimazione
ai centesimi
Approssimazione
per difetto
__
26,6592
11,28
✗
26,66
18,2321
18,23
✗
64,37
___
64,3695
Approssimazione
per eccesso
✗
✗
3 Completa la tabella approssimando ai millesimi i seguenti numeri decimali e indica con una
crocetta il tipo di approssimazione:
Approssimazione
ai millesimi
Approssimazione
per difetto
Approssimazione
per eccesso
4,686
✗
618,343
✗
178,29985 16,78653 178,300
16,786
✗
Numero
4,68593
__
618,34332
✗
4 Trasforma le seguenti frazioni in numeri decimali e approssima questi ultimi ai decimi:
–
2
___
= 0,13 → 0,1
15
18 0,45 → 0,4
___
= ...................................................................................................................................................................................................
40
50 2,27 → 2,3
___
= ..................................................................................................................................................................................................
22
16 0,53 → 0,5
___
= ...................................................................................................................................................................................................
30
86 2,38 → 2,4
___
= ..................................................................................................................................................................................................
36
14 0,194 → 0,2
___
= ...................................................................................................................................................................................................
72
5 Svolgi i seguenti calcoli e approssima il risultato ai centesimi:
(1,6 + 3,04) × 0,6 =
4,64 × 0,6 = 2,78
..............................................................................................................................................................
2,25 × 3,6 = 8,10
(2 − 0,5 + 0,75) × 3,6 = ....................................................................................................................................................
6 Approssima ai centesimi i numeri decimali, svolgi i calcoli e approssima il risultato ai decimi:
__
__
__
___
__
× 3 − 0,84 = 3,5
(0,615 + 0,33 + 0,5) × 3 − (0,23 + 0,512 + 0,1 ) = ..1,44
...................................................................................
__
__
__
3 + 1,25 + 0,70 = 4,9
3 + (0,75 + 0,5) + (0,26 + 0,43 ) = ...........................................................................................................................
8
Unità
L'angolo
del problema
1
1 Calcola il valore approssimato ai decimi della seguente espressione:
__
__
__
__
9,2 − (0,3 + 3,5 − 1,2 ) × 1,5 × 1,3 + 0,6 =
Ti do una mano...
Trasformiamo in frazione tutti i numeri decimali:
( 9
)
3
11
15
12
6
......
......
......
......
3 35 − ......
92
___
− ___
× ___
− __
+ _______
× ___
+ ___
=
10
9
9
......
10
......
9
......
10
Semplifichiamo dove possibile:
(
)
32 ......
11
3 1 ......
4 2 ......
3
......
46
1 ......
− ___
+ ___
× ___
+ ___
=
× ___
___ − __
......
9
9
2 1 ......
3 1 ......
5
5
3
Svolgiamo i calcoli:
)
24 8
............
67
3 138 − 80 + 9 __
3 46 16 __
46
= = 4,5
+ = _____________
2 + __ = __ − __
× ...................................................................................................................................................................
___ − _____
5
5
5
93
3
15
5
15
(
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
[4,5]
2 Calcola il valore approssimato ai centesimi della seguente espressione:
__
__
__
__
__
(0,31 + 0,15 ) : (0,85 − 0,16 ) + 1 − 0,4
Prova da solo!
28
( 90
14
90
77
) ( 90
15
90
)
4
9
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
__
+ __
: __
− __
+ 1 − __
=
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
62
)
( 90 ) ( 90
90 1
62 31
42
4 42
4
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
__
: __
+ 1 − __
= __
× __
+ 1 − __
=
21
9
90
1
9
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
189 + 279 − 124
279
344
21
4
______________
__
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
+ 1 − __
=
= ___
= 1,23
31
9
279
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
[1,23]
9