6. Moto uniformemente accelerato
posizione
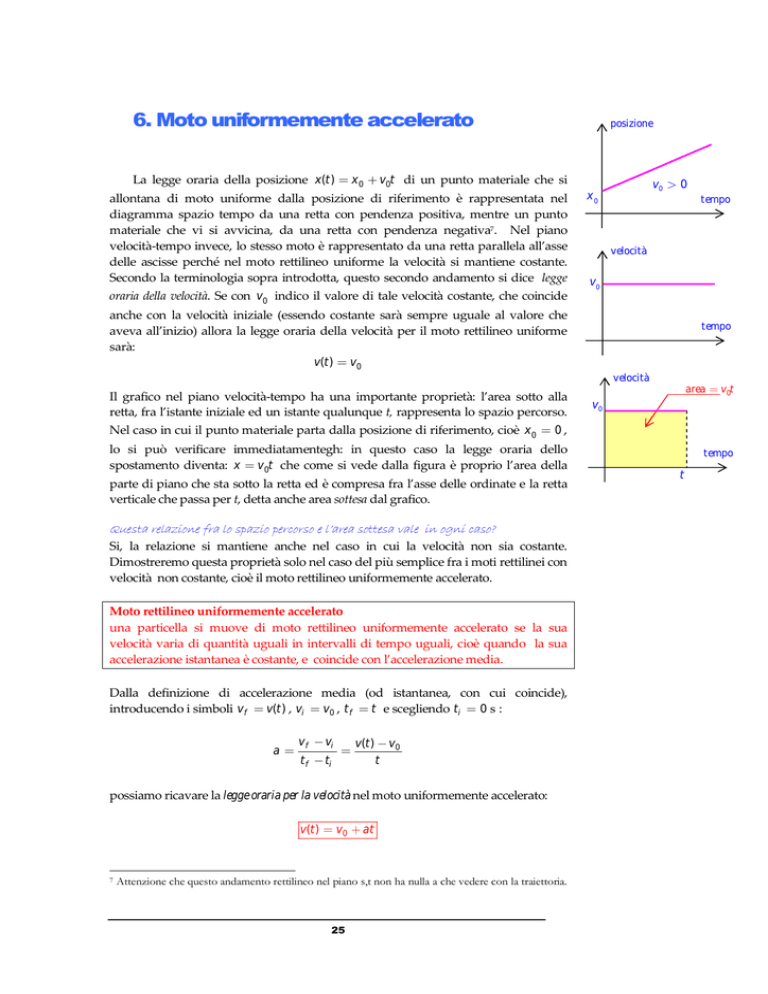
La legge oraria della posizione x (t ) x 0 v0t di un punto materiale che si
allontana di moto uniforme dalla posizione di riferimento è rappresentata nel
diagramma spazio tempo da una retta con pendenza positiva, mentre un punto
materiale che vi si avvicina, da una retta con pendenza negativa7. Nel piano
velocità-tempo invece, lo stesso moto è rappresentato da una retta parallela all’asse
delle ascisse perché nel moto rettilineo uniforme la velocità si mantiene costante.
Secondo la terminologia sopra introdotta, questo secondo andamento si dice legge
oraria della velocità. Se con v0 indico il valore di tale velocità costante, che coincide
v0 0
x0
tempo
velocità
v0
anche con la velocità iniziale (essendo costante sarà sempre uguale al valore che
aveva all’inizio) allora la legge oraria della velocità per il moto rettilineo uniforme
sarà:
v(t ) v0
tempo
velocità
Il grafico nel piano velocità-tempo ha una importante proprietà: l’area sotto alla
retta, fra l’istante iniziale ed un istante qualunque t, rappresenta lo spazio percorso.
Nel caso in cui il punto materiale parta dalla posizione di riferimento, cioè x 0 0 ,
lo si può verificare immediatamentegh: in questo caso la legge oraria dello
spostamento diventa: x v 0t che come si vede dalla figura è proprio l’area della
parte di piano che sta sotto la retta ed è compresa fra l’asse delle ordinate e la retta
verticale che passa per t, detta anche area sottesa dal grafico.
Questa relazione fra lo spazio percorso e l’area sottesa vale in ogni caso?
Si, la relazione si mantiene anche nel caso in cui la velocità non sia costante.
Dimostreremo questa proprietà solo nel caso del più semplice fra i moti rettilinei con
velocità non costante, cioè il moto rettilineo uniformemente accelerato.
Moto rettilineo uniformemente accelerato
una particella si muove di moto rettilineo uniformemente accelerato se la sua
velocità varia di quantità uguali in intervalli di tempo uguali, cioè quando la sua
accelerazione istantanea è costante, e coincide con l’accelerazione media.
Dalla definizione di accelerazione media (od istantanea, con cui coincide),
introducendo i simboli v f v(t ) , vi v0 , t f t e scegliendo ti 0 s :
a
v f vi
t f ti
v(t ) v0
t
possiamo ricavare la legge oraria per la velocità nel moto uniformemente accelerato:
v(t ) v0 at
7
Attenzione che questo andamento rettilineo nel piano s,t non ha nulla a che vedere con la traiettoria.
25
area v 0t
v0
tempo
t
velocità
v v 0 at
Per motivi analoghi a quelli visti nel caso di x x 0 vt nel piano posizione-tempo,
anche il grafico di v v0 at nel piano velocità-tempo è una retta. Infatti il
rapporto fra la variazione dell’ordinata v e la variazione dell’ascissa t è
costante, v / t a , e come abbiamo visto questo è possibile solo lungo i punti
v0
di una retta. Inoltre, per analogia con il caso v v0 , possiamo interpretare l’area
sottesa dalla retta v v0 at
A
tempo
nel piano velocità-tempo come lo spazio
complessivamente percorso. Se infatti immaginiamo di effettuare il moto in tanti
tratti di durata t percorsi a velocità costante, in modo che la velocità cresca a
scalini e non con continuità, si vede bene che l’area sotto alla retta è approssimabile
tramite quella dei rettangoli, che in base a quanto detto prima, rappresentano lo
spazio percorso in ciascuno dei tratti. La retta può essere interpretata come il caso
limite in cui ciascuno degli intervalli t diventa piccolissimo.
Come si ricava la legge oraria per la posizione in questo moto?
velocità
Supponendo che il punto parta dalla posizione x 0 0 , lo spazio percorso in totale
v v 0 at
v
v0
coincide direttamente con la posizione x (t ) . Con riferimento alla figura, si tratta di
calcolare l’area del trapezio evidenziato, ottenibile facendo “la metà della somma
delle basi” (di misura v0 e v ) e moltiplicandola per “l’altezza” t :
x (t ) A 1 (v v0 )t
2
A
tempo
Inserendo in questa relazione la legge oraria della velocità v v0 at :
t
x (t ) 1 [(v0 at ) v0 ]t v0t 1 at 2
2
2
Nel caso più generale dovremo aggiungere ad x (t ) la posizione iniziale x 0 :
x (t ) x 0 v0t 1 at 2
2
Relazione che costituisce la legge oraria della posizione per il moto rettilineo
uniformemente accelerato.
Come si calcola la velocità media in un moto rettilineo uniformemente accelerato?
Ci proponiamo ora di calcolare la velocità media di un tale moto. Ricordiamo che la
velocità media è quella per cui se lo stesso spostamento venisse percorso con
velocità costante pari ad essa, complessivamente la particella impiegherebbe lo
stesso tempo. Da questa definizione segue che che se x 0 0 allora risulta:
x (t ) vm t
che, confrontata con la precedente x (t ) 12 (v v0 )t fornisce vm 12 (v v0 ) ,
risultato noto come:
26
Teorema della velocità media
in un moto uniformemente accelerato la velocità media vm fra l’istante iniziale ed
un istante t è la media fra la velocità iniziale e quella all’istante t :
vm 12 (v v0 )
Il risultato si generalizza anche al caso di un qualsiasi primo istante, non
necessariamente quello iniziale del moto.
Esempio 41
Si studi il moto rettilineo uniformemente accelerato: x (t ) 5.0 3.5 t 4.2t 2 .
Analizziamo la legge oraria. Si deduce:
1) Che un punto materiale è partito dalla posizione x 0 5.0 m dove aveva una
velocità diretta nel verso scelto come positivo e con intensità: v0 3.5 m/s . Infatti
un confronto con l’espressione simbolica fornisce immediatamente il valore costante
di accelerazione: a 8.4 m/s 2 il che significa che la sua velocità varia, aumentando
l’intensità di: 8.4 m/s ogni secondo che passa.
2) Che la velocità aumenti non lo vediamo dal fatto che il segno dell’accelerazione è
positivo: questo indica solo che ogni secondo vengono aggiunti alla velocità
8.4 m/s nel verso scelto da noi come positivo sulla traiettoria. Questo verso non ha
legami con il verso in cui il punto percorre la traiettoria: se ad esempio il punto si
stava muovendo indietro, un’accelerazione positiva di 8.4 m/s 2 corrisponde ad
una diminuzione del modulo della velocità, se invece il punto si stava movendo
avanti, corrisponde ad un aumento del modulo. Che si tratti di un aumento di
velocità lo vediamo allora dal fatto che la velocità iniziale ha lo stesso segno
dell’accelerazione.
3) Essa inoltre aumenta in modo uniforme, cioè ad esempio fra dieci ed undici
secondi la velocità crescerà di 8.4 m/s proprio come fra cento e centouno secondi e
non di un valore differente di volta in volta. Questo può essere scritto sinteticamente
tramite la legge oraria della velocità: v(t ) 5.0 8.4t e quindi se volessimo
calcolare la velocità e la posizione dopo 2.0 s basterà sostituire il valore dato al
posto del tempo:
x (2.0 s) (5.0 3.5 2.0 4.2 2.02 ) m 29 m
v(2.0 s) (3.5 8.4 2.0) m/s 20 m/s
0.0 m
v(0) 3.5 m/s
v(2.0) 20 m/s
x (0) 5.0 m
x (2.0) 29 m
Esempio 42
Si studi il moto rettilineo uniformemente accelerato seguente, calcolando in
particolare quando la particella si ferma ed in quale istante attraversa l’origine:
x (t ) 8.5 9.6t 0.60t 2
27
Esempio 43
Una ragazza fa jogging correndo alla velocità costante di 4.0 m/s . Ad un certo
istante passa davanti ad un uomo seduto su di una panchina e comincia a rallentare
costantemente di 0.40 m/s ogni secondo. Questo riflette per 5.0 s e decide di
conoscerla, quindi scatta con velocità iniziale di 3.0 m/s accelerando il passo in
maniera costante con a 8.0 m/s2 . A quale distanza dalla panchina il tizio
raggiunge la ragazza? Che velocità possiedono entrambi in quell’istante? Usciranno
insieme quella sera stessa?
Scriviamo le leggi orarie, posizione e velocità, di entrambe le persone. La prima cosa
da fare è scegliere una origine della traiettoria (rettilinea) che sarà la posizione della
panchina. Poi occorre uno stesso istante iniziale opportuno per entrambi: qui
conviene il momento in cui il tizio si alza per iniziare la sua corsa. La legge oraria
della posizione dell’uomo si ottiene facilmente:
x 0U 0.0 m , v0U 3.0 m/s ed aU 8.0 m/s 2 ,
xU (t ) 3.0t 4.0t 2
Più complesso è scrivere la legge oraria della ragazza, della quale nel riferimento
scelto è nota soltanto l’accelerazioneaR 0.40 m/s2 :
x R (t ) x 0R v0Rt 0.20t 2
La posizione iniziale della ragazza x 0R è lo spazio di cui si è allontanata dalla
panchina in 5.0 s e la sua velocità iniziale v0R quella che ha dopo aver decelerato
per gli stessi 5.0 s . Per calcolare questi dati dobbiamo scrivere dapprima un’altra
equazione oraria per la sola ragazza, che abbia però come istante iniziale quello del
passaggio alla panchina. In questo riferimento si ha x 0R 0.0 m e v0R 4.0 m/s ,
mentre l’accelerazione è sempre aR 0.40 m/s2 :
x R (t ) 4.0t 0.20t 2 x R (5.0 s) (4.0 5.0 0.20 5.02 ) m 15 m
vR (t ) 4.0 0.40t vR (5.0 s) (4.0 0.40 5.0) m/s 2.0 m/s
Riscriviamo quindi l’equazione oraria della ragazza usando come istante iniziale
quello in cui il tizio si alza dalla panchina, in modo da poterla confrontare con
quest’ultima. In questo secondo caso la posizione iniziale della ragazza sarà allora
x 0 15 m e la velocità iniziale v0 2.0 m/s , da cui:
x R (t ) 15 2.0t 0.20t 2
Nell’istante in cui si raggiungono, le due posizioni xU (t ) e x R (t ) devono essere
uguali, pertanto imponiamo questa condizione per trovare il tempo:
15 2.0t 0.20t 2 3.0t 4.0t 2
4.2t 2 1.0t 15 0 t1 1.8 s t 2 2.0 s
dove la seconda soluzione matematica non ha significato fisico perché l’incontro
avverrebbe prima del nostro istante iniziale. Il calcolo delle velocità d’incontro si fa
tramite le relative leggi orarie:
vR (t ) 2.0 0.40t vR (1.8 s) 1.3 m/s
vU (t ) 3.0 8.0t vU (1.8 s) 17 m/s
I due non usciranno insieme quella stessa sera perché il tizio ha accelerato troppo e
così le sfreccia affianco senza poterle dire neanche una parola…
28












