FISICA-TECNICA Trasmissione del calore II parte

Geometrie cilindriche
FISICA-TECNICA
Trasmissione del calore
II parte
Vediamo ora quando
abbiamo pareti cilindriche:
Q = −kA
dT
dT
= −k 2πrL
dr
dr
dr
= − k 2πrLdT
r
re
Te
dr
Q ∫ = −k 2πrL ∫ dT
r
ri
Ti
Q
re
Katia Gallucci
ri
r
L
Q ln
Q=
re
= − k 2πL(Te − Ti )
ri
− k 2πL(Te − Ti )
r
ln e
ri
1
Esempio
Calcolare il calore dissipato da un tubo lungo 300 cm che
ha raggio interno 2,5 cm e raggio esterno 2,8 cm
(k=30kcal/hm°C),Ti=300°C e Te=295°C
Q=25.103kcal/h
Consideriamo ora la presenza di uno strato isolante intorno
al tubo di raggio 5 cm ed una temperatura esterna di parete
di 50°C:
2πL(Ti − Te )
Q=
r
r
ln e ln isolante
ri
re
+
k
kisolante
2
tubo isolante
film aria
Q = 2πL∆Trisolante hconv =
2πL∆T
1
risolante hconv
Possiamo esprimere la resistenza
totale, in un caso più realistico come
somma della resistenza dovuta
all’isolante e una dovuta alla
convezione
300°C
50°C
ln
Rtot =
25°C
risolante
re
kisolante
+
1
risolante hconv
Q=230kcal/h
3
4
É necessario scegliere un isolante che abbia kisolante piccolo
in modo che rmin sia minore di re. Se rmin>re l’applicazione
dell’isolante nell’intervallo rmin-re è controproducente.
Se facciamo la derivata della resistenza totale e la
uguagliamo a zero, così troviamo il valore del raggio per il
quale la resistenza è minima:
1
1
dRtot
=
− 2
=0
dr
kisolante r r hconv
rmin
1
kisolante r
=
1
r hconv
2
risolante
k
= isolante
hconv
re
A parità di hconv che non possiamo variare perché dipende
dalle condizioni dell’aria ambiente, la resistenza è minima
per un valore rmin che dipende da kisolante
rmin
Rtot
5
Perdite di calore per convezione naturale
da un tubo orizzontale
tubo isolante
film aria
300°C
38°C
ri
re
r
26°C
6
Poniamo r=x (la nostra incognita)
Calcolare lo spessore di
isolante necessario da
applicare ad un tubo
orizzontale che ha raggio
ri=2,5cm e re=2,8cm
(k=30kcal/hm°C), Ti=300°C,
l=3m considerando una
temperatura esterna
dall’isolante di 38°C e l’aria
circostante alla pressione
atmosferica e a 26°C
(Kisolante=0,05kcal/hm°C)
7
Q=
2πL(Ti − Te )
= 2πL∆Txhconv
r
x
ln e
ln
ri
re
+
k
kisolante
È tutto noto tranne hconv che dobbiamo calcolare.
Per la convezione naturale vale la relazione:
Nu =
hconv D
= ψ Pr i Gr n
k
Per tubi orizzontali si può utilizzare la relazione:
Nu = 0,525 Pr 0, 25 Gr 0, 25 Gr = D 3
Pr =
1
µ2
ρ 2 β g∆T
cpµ
k
8
(300 − 38) = x10− 22,86 3,7810−3 + 20 ln
Le proprietà dell’aria le consideriamo alla temperatura
media (38+26)/2=32°C
µ = 0,0684 kg/mh
k = 0,023 kcal/m°Ch
ρ = 1,157 kg/m3
cp = 0,241 kcal/kg°C
β = 0,00328(1/°C)
g = 1,27.108 m/h2
D=?
Dobbiamo ipotizzare un diametro esterno dell’isolante
1°hp D=36cm=0,36m→ hconv=2,86kcal/(hm2°C)
(38 − 26)


x 

2,8 
x 

763,4 = x 3,7810− 3 + 20 ln

2,8 

x 

763,4 − x 3,7810 − 3 + 20 ln
 = f ( x)
2,8 

x = 17 ⇒
x = 19 ⇒
f ( x) = 150
f ( x) = 35,7
x = 20 ⇒
f ( x) = −23,1
x = 19,5 ⇒
f ( x) = 6,5
OK.
9
Q = 2πLr∆Thconv = 2π ⋅ 3 ⋅ 0,195 ⋅ 12 ⋅ 2,86 = 126
kcal
h
10
Verifichiamo che rmin è inferiore a re
Flusso attraverso il tubo:
Q=
− k 2πL∆T
r
ln e
ri
⇒ 126
kcal 30 ⋅ 2π ⋅ 3 ⋅ (300 − T )
=
⇒ T = 299,975°C
2,8
h
ln
2,5
Flusso attraverso l’isolante:
Q=
− k 2πL∆T
r
ln e
ri
⇒ Q=
rmin
kcal
0,05
kisolante
hm°C = 0,0175m = 1,75cm
=
=
kcal
hconv
2,86 2
hm °C
Se invece di un materiale isolante si fosse utilizzato
un materiale tipo cemento (k=0,78kcal/hm°C), il rmin
sarebbe stato 0,27 quindi il tubo avrebbe perso più
calore.
kcal
0,05 ⋅ 2π ⋅ 3 ⋅ (299,975 − 38)
≅ 127
19,5
h
ln
2,8
11
12
Irraggiamento
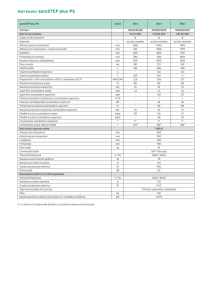
Materiale
k (cal/hm°C)
k (W/m°C)
Gas a P=1atm (aria a 0°C) 0.0176
0.0205
Lana di vetro a 25°C
0.034
0.0395
Legno a 20°C
0.15
0.174
Granito a 50°C
2.7
3.14
Acciaio a 30°C
30
34.88
Argento a 0°C
360
418.6
Cemento a 20°C
0.78
0.907
13
Qualunque corpo, a qualunque temperatura, emette
energia sotto forma di onde elettromagnetiche.
Di tutte le radiazioni emesse, interessano solo quelle le
cui caratteristiche dipendono esclusivamente dalla
temperatura del corpo che le emette, senza l’aiuto di un
altro mezzo: a tali radiazioni si dà il nome di radiazione
termica.
Quando dunque si parla di radiazione termica si intende
l’energia calorifica emessa da un corpo solo in virtù della
sua temperatura.
Rispetto alla conduzione e convenzione, l’irraggiamento
può verificarsi nel vuoto e non dipende dai salti termici.
14
Nel caso dell’irraggiamento il calore si propaga sotto
forma d’onde elettromagnetiche, che si propagano e
trasportano energia da un punto ad un altro.
Le onde elettromagnetiche comprendono anche, tra
le altre, le onde radio, le microonde, i raggi X e γ.
Queste onde sono prodotte da fenomeni fisici
diversi, tutti riconducibili ad uno stato d’eccitazione
dei componenti elementari della materia.
15
16
Se un corpo è a temperatura superiore allo zero
assoluto, la sua superficie emette radiazioni,
prevalentemente concentrate tra le lunghezze
d'onda di 0,1 e 1000 µm.
A differenza degli altri casi (conduzione e
convezione) nei quali il flusso va dal corpo a
temperatura superiore a quello a temperatura
inferiore, nel caso dell’irraggiamento, due corpi che
si “vedono” irraggiano calore l’uno verso l’altro. Il
calore netto trasportato è quindi dato dalla
differenza dei due flussi e fluisce verso il corpo a
temperatura minore.
L’irraggiamento riveste particolare
importanza per quanto attiene:
alla radiazione solare incidente sulle pareti
degli ambienti (d’estate, soprattutto quelle
trasparenti, come le vetrate);
allo scambio di energia radiante tra gli
occupanti e le pareti dell’ambiente;
ai forni di cottura o riscaldamento, sia
convenzionali che a microonde.
17
Esempio di irraggiamento solare in un ambiente
attraverso la finestra in inverno ed in estate.
18
L’energia irraggiata dipende esclusivamente dalla
temperatura del corpo secondo la relazione::
E = εσ T 4
19
E= energia irradiata per unità di superficie e nell’unità di
tempo
ε=emissività (o potere emissivo) del corpo
σ=costante di Stefan-Boltzmann=4,88.10-8kcal/m2hK4 =
5,67.10-8 J/sm2K4
T=temperatura assoluta, K
20
Si definisce
coefficiente di emissione monocromatica per la
frequenza ν (detto anche potere emissivo o
emittanza monocromatica) ε((ν)), il rapporto tra
l'energia emessa in tutte le direzioni, nell’unità di
tempo, per unità di superficie e nell'intervallo di
frequenza [ν,ν+dν ] dal corpo in esame e l'energia
emessa dal corpo nero alla stessa temperatura;
L’emissività ha valori compresi tra 0 e 1.
21
Il calore trasportato per irraggiamento, passa da un
corpo all'altro, anche nel vuoto, senza che la
sostanza eventualmente interposta (purché
trasparente alla radiazione) partecipi al fenomeno.
Nel vuoto la velocità di propagazione è
rigorosamente la stessa per tutte le radiazioni e,
quindi, anche per la luce; essa vale:
c=3,00.108 ms-1
pertanto nel vuoto si ha:
λ = ct=c/ν
22
23
Quando l'energia raggiante raggiunge un corpo è in
parte assorbita, riflessa e trasmessa da esso. La
parte assorbita va ad eccitare i costituenti
elementari del corpo, che a sua volta emette
radiazioni e così via.
Vale, cioè, la relazione:
a+ r + t =1
frazione di energia assorbita + frazione di
energia riflessa + frazione di energia trasmessa
24
Si dice opaco un corpo per cui è a + r = 1 e t
= 0; è invece definito trasparente un corpo
per cui è t = 1 e a = r =0.
È però bene ricordare che i concetti di
“opaco” e di “trasparente” non sono assoluti,
ma sono relativi alla lunghezza d'onda della
radiazione incidente.
Si definisce lunghezza d’onda λ (lambda), in una certa
direzione, la distanza λ=vt percorsa dall’onda, con
velocità di propagazione v, nel periodo t, ossia durante il
tempo dopo il quale il fenomeno si ripete eguale a sé
stesso. Si dice frequenza ν il reciproco del periodo t.
25
26
Si definisce coefficiente di assorbimento
monocromatico (ossia per la generica
frequenza ν ), il rapporto tra l’energia
assorbita e l’energia incidente da tutte le
direzioni, nell’unità di tempo e di superficie,
nell’intervallo di frequenza [ν,ν+dν]; ossia:
a(ν)=qo(ν)/qi(ν)
Si dice grigio un corpo per il quale a non è
funzione di ν.
27
Si dice invece corpo nero un corpo per il quale a=1,
ossia che assorbe tutta l’energia incidente.
Il corpo nero è un'astrazione; esso può essere simulato
da una sfera cava dalla quale la radiazione ha poche
probabilità di uscire se le pareti non sono perfettamente
riflettenti.
28
L’irraggiamento è descritto da alcuni modelli fondamentali.
La legge di Plank (1858-1947) consente di calcolare l'energia
radiante emessa dal corpo nero per unità di tempo, di superficie e di
lunghezza d'onda (emittanza monocromatica) nell'intervallo
[λ,λ+dλ]:
dove:
k=1,3802 10-6 è la costante di Boltzman
h=6,6236 10-27 erg.s è la costante di Plank
c=3,00.108 m.s-1 è la velocità della luce.
Integrando l'espressione precedente su tutto lo spettro si ottiene:
dove F12 e F21 sono le frazioni di radiazione emesse da ciascuno
dei due corpi che raggiungono l'altro; i valori di F12 e F21
dipendono dalla geometria del sistema.
dove qbe è l'emittanza totale e σo = 5,67 *10-8 W/m2K4=4,88*10-8
kcal/hm2K4è la costante di Stefan-Boltzman.
Abbiamo così calcolato l'emittanza totale del corpo nero; questa
equazione è detta legge di Stefan-Boltzman.
29
Si noti che è F12S1= -F21S2, dato che, se si pone T1=T2, è
q12=0. Nel caso di superfici nere affacciate è,ad esempio,
F12=F21=1, mentre per un corpo completamente contenuto
in un altro convesso (prodotto in un forno), indicata con 1
la sua superficie, è F12=1 e F21=S1/S2. I valori di F sono
riportati nei manuali per i casi più comuni.
30
Per i corpi grigi l'analisi è in generale molto difficile; nel
caso di superfici affacciate si ha, ad esempio:
con
q12=εmσoS1(T14-T24)
εm =
1
ε1
+
1
ε2
Calcolando il valore della lunghezza d'onda per il quale la legge
di Plank presenta un massimo, si ottiene la legge dello
spostamento (1886) di Wien (1864-1928):
Tλmax= 0,2884 cmK
Questa legge consente di conoscere il valore della lunghezza
d'onda per cui é massima l'emittanza monocromatica nota T o
viceversa.
Nel caso dei corpi grigi, l'emittanza totale si ottiene moltiplicando
quella del corpo nero per il coefficiente di emissione, sempre
minore di 1, come sopra già ricordato.
Ricordando la legge di Stefan-Boltzman, si può calcolare la
potenza termica scambiata tra due corpi neri; essa vale:
q1↔2 = q1→2- q2→1 = F12S1σoT14 - F21S2σoT24
L’energia irradiata in tutte le direzioni se incidesse su un
secondo corpo potrebbe essere parzialmente riflessa o
assorbita a trasmessa.
La frazione r dell’energia che viene riflessa, determina il
potere riflettente; la frazione a che viene assorbita
determina il potere assorbente. La frazione τ costituisce
la trasparenza (se τ è trascurabile il corpo è detto
termicamente opaco)
Per ogni corpo è valida la relazione :
r+a+τ=1
Se a=1 si ha il corpo nero capace di assorbire tutta
l’energia incidente su di esso.
−1
31
32
La legge di Kirchoff
Ad ogni temperatura qualsiasi corpo è capace di
irraggiare la stessa energia che è in grado di
assorbire.
a=ε
Questa legge, sperimentalmente dimostrata, è
teoricamente giustificabile in base alla termodinamica.
Un corpo non nero ha un potere emissivo e assorbente,
ad una certa temperatura, pari a
E = a σT
Se il potere assorbente o l’emissività non varia con la
temperatura, allora un corpo non nero è assimilabile ad
un corpo grigio.
Se T1 e T2 sono le temperature di un corpo e
dell’atmosfera, e T1>T2, il calore scambiato vale:
E = a1σT14 − a2σT24 = σ (a1T14 − a2T24 )
a1= emissività del corpo 1 alla temperatura T1
a2= emissività del corpo 2 alla temperatura T2 che di
solito viene valutato uguale al valore di a1 alla
temperatura T2
4
dove a è la frazione dell’unità che rappresenta il potere
assorbente del corpo, e anche l’emissività
33
Il calore che fluisce dal gas attraverso le pareti per effetto
della convezione è:
Esempi
34
Calcolo del calore ceduto per irraggiamento da un tubo di
1 m (de=5cm) che si trova alla temperatura di 130°C,
mentre la temperatura dell’ambiente è 15°C (a=0,7)
Un gas alla temperatura di 1090°C contiene il 5% di
vapore d’acqua e fluisce alla pressione atmosferica
attraverso una canna fumaria a sezione quadrata di 60
cm di lato, di mattoni refrattari. Calcolare la potenza
termica che viene scambiata per metro di lunghezza delle
pareti dal gas, se la superficie interna è di 1000°C e
hv=10kcal/hm2K
35
Q = hv A(TG − TP ) = 10 ⋅ 4 ⋅ 0.6 ⋅ 180⋅ = 1920
kcal
h
Per il calcolo del calore irraggiato si opera in questo modo:
1.
Calcolo del raggio della semisfera equivalente L
L = 3.4
2.
volume
0.6 2 ⋅1
= 3.4
= 0.51m
area bagnata
0.6 ⋅ 4 ⋅1
Calcolo del prodotto PL (P=%vapore.pressione totale=
pressione parziale del vapore)
P ⋅ L = 0.05 ⋅ L = 0.05 ⋅ 0.51 = 0.0255m ⋅ atm
3.
Calcolo dell’emissività del vapore d’acqua con il grafico
a 1363K e 1283K
36
Emissività del vapor d’acqua con T e
correzione Ptot
a1= 0.035 (a T=1363K)
a2=0.039 (a T=1283K)
I due valori devono essere corretti per la pressione
(P+Ptot)/2=(0.05+1)/2≈0.5 atm.
a1CP ≈a1
In definitiva:
Qirr=4.8810-8(0.6.4.1)(0.035.13634-0.039.12834)=1771kcal/h
Qtot=Qirr+Qconv=1771+1920=3691kcal/h
37
38
39
40
Se fosse presente la CO2 :diagrammi
Si calcola la L e si moltiplica la pressione parziale della
CO2 con L e si ottiene il valore PL. Si entra nel grafico nel
grafico con la temperatura e si trova a
Scambiatori di calore
Per sapere a corretto con la pressione si calcola il rapporto
(P+Ptot)/2 e si determina il CP dal secondo diagramma
a =aCP
Quando sono presenti CO2 e H2O l’emittanza può essere
calcolata sommando le emittanze dei componenti.
41
Scambiatore di calore
42
Si dice scambiatore di calore un dispositivo
nel quale avviene il trasferimento di calore tra
due fluidi.
43
Esistono molti tipi di scambiatori, classificabili per tipo di
utilizzo, di contatto tra i fluidi, di direzione dei flussi, di
forma.
In particolare è importante la direzione dei flussi, che
possono essere.
44
Gli scambiatori generalmente più utilizzati
sono quelli detti a fascio tubiero.
Nel campo alimentare sono anche molto diffusi gli
scambiatori a piastre per la loro compattezza e per la
facilità di pulizia (e/o sterilizzazione).
45
Il dimensionamento degli scambiatori di calore è
fatto dal costruttore sulla base di specifiche fornite
dal cliente. Ciononostante è utile conoscere i criteri
adottati, per poter utilizzare questi importanti
componenti degli impianti a ragion veduta.
Il problema fondamentale consiste nel calcolo della
superficie di scambio necessaria per portare una
certa quantità di fluido da una certa temperatura ad
un’altra, cedendo o assorbendo calore a/da un altro
fluido, note le temperature di ingresso e di uscita,
ovvero la portata e una delle due temperature di
quest’ultimo.
Per risolvere questo problema occorre calcolare
preliminarmente la quantità di calore che i due fluidi
debbono scambiare.
47
46
Il flusso di calore da scambiare si ottiene scrivendo il
bilancio energetico globale dello scambiatore:
48
Facendo ricorso ad H=U+pV e tenendo conto che nella
maggioranza dei casi è non c’è variazione di quota e di
velocità, l’equazione di bilancio può essere scritta per i
due fluidi rispettivamente come segue:
H1i+(q1/M1)=H1u
H2i+(q2/M2)=H2u
dalle quali si possono ricavare:
q1=(H1u-H1i)M1
q2=(H2u-H2i)M2
Poiché sappiamo che il flusso di calore scambiato tra i
due fluidi sono eguali ma di segno contrario (acquisito e
ceduto), ossia che è q=q1=-q2, dalle due espressioni
precedenti si ottiene:
q =(H1i-H1u)M1=(H2u-H2i)M2
detta equazione di bilancio energetico globale dello
scambiatore
Se:
i due fluidi subiscono all’interno dello scambiatore cadute
di pressione (perdite di carico) piccole rispetto al valore
delle rispettive pressioni,
non avvengono cambiamenti di stato,
i calori specifici dei due fluidi possono ritenersi costanti
lungo il percorso (variano cioè poco in funzione della
temperatura)
l’espressione precedente assume la forma:
q= cp1(T1i-T1u)M1= cp2(T2i-T2u)M2
49
Calcoliamo ora la superficie di scambio, prendendo in
considerazione per lo scambiatore la più semplice
architettura e i due flussi equi- e contro-corrente.
Individuiamo una generica porzione infinitesima dello
scambiatore di lunghezza dx alla distanza x dall’ingresso
del fluido 1 e la cui area della superficie di scambio valga
dSx .
50
Siano T1 e T2 le temperature dei due fluidi. Il flusso di
calore trasmesso da un fluido all’altro (positivo se
uscente) attraverso la sezione dS vale
dq=U(T1 -T2)dSx
dove U è il coefficiente globale di trasmissione del
calore.
Scrivendo il bilancio energetico per i due fluidi
relativamente al tratto di scambiatore considerato si ha:
dq=-dq1=-M1dH1=-M1cp1dt1
dq=dq2=±M2dH2=±M2cp2dt2
dove:
51
le eguaglianze di destra sono valide per ∆p < < p e cp=cost
Nel caso del fluido 2, il segno “+” vale per scambiatore
equicorrente (H cresce con Sx) e quello “-” per scambiatore
controcorrente (H diminuisce con Sx).
52
La costante di integrazione si calcola sapendo che:
T1i-T2i (equicorrente)
T1i-T2u (controcorrente)
per Sx=0 è (T1-T2)=∆To, essa vale cost=-ln ∆To
Pertanto l’espressione precedente diventa:
Ricavando dalle precedenti -dT1 e dT2,
Sommando: -dT1+dT2= d(T2-T1)=dq(1/M1cp1± 1/M2cp2)
Ricordando che dq = U(T1-T2)dSx e sostituendo nella
precedente si ottiene:
d(T2-T1)= U(T1-T2) (1/M1cp1± 1/M2cp2) dSx
che, nelle ipotesi cp e U costanti, separando le variabili
(T1-T2) e Sx e integrando diventa:
 1
1
− ln (T1 − T2 ) = U 
±
 M 1c p 1 M 2 c p 2

 1
1
− ln (T1 − T2 ) = U 
±
 M 1c p 1 M 2 c p 2


 Sx + cost

Calcolando quest’ultima per S=Sx per cui è (T1-T2)=
T1u-T2u (equicorrente)
T1i-T2i (controcorrente)
 1
si ottiene:
1 
− ln ∆TS = U 
±
S − ln ∆T0
 M1c p 1 M 2 c p 2  x


ln
53
Ricordando che è:
∆T0
T −T
1
= − 1u 1i
M 1c p1
q
T −T
1
= − 2 u 2i
M 2c p 2
q
US  − (T1u − T1i ) ± (T2u − T2i ) 
si ha, infine: ln ∆Ts =
q
Semplici passaggi consentono di verificare che in entrambi i
casi di equi- e contro-corrente, vale sempre l’espressione:

 Sx − ln ∆T0

 1
∆T0
1
=U
±
 M 1c p 1 M 2 c p 2
∆TS


 Sx

54
Un impiego frequente degli scambiatori di calore è quello
per il recupero del calore.
∆T0 US [ ∆T0 − ∆Ts ]
=
∆Ts
q
US [ ∆T0 − ∆Ts ]
q
q=
= US ∆Tm ⇒ S =
∆T
U ∆Tm
ln 0
∆Ts
ln
∆Tm viene chiamato ∆T medio logaritmico o, nei testi
inglesi, MLDT.
Si noti che ∆Tm è stato calcolato assumendo U costante il che
generalmente non è vero; utilizzando però un valor medio di
U nell’intervallo delle temperature in gioco si ottiene una
buona approssimazione.
55
Il prodotto si pre-riscalda nel primo scambiatore, si tratta
a caldo nel secondo, si pre-raffredda di nuovo nel primo,
asportando parte del calore speso per trattarlo e
utilizzandolo per pre-riscaldarlo in ingresso, e si
raffredda nel terzo.
56
Per stabilire la convenienza del recupero di calore si
traccia la curva somma dell’ammortamento annuale dei
costi di impianto e quella dei costi di esercizio; si
dimensiona il recupero in corrispondenza del minimo di
questa curva.
Scambio termico in equicorrente e in
controcorrente
Abbiamo visto che nello scambio termico, trascurando
l’irraggiamento, possiamo utilizzare la relazione:
Q=AUD∆T
Consideriamo due tubi coassiali nei quali scorrono due
fluidi con temperature diverse
Equicorrente
T1
T1
T’1
T2
T’2
T’1
T’2
L
T2
L
57
58
Controcorrente
T’1
T1
T1
T2
T’2 T’
L
T’2
1
Equicorrente
∆TLMDT =
(T1 − T2 ) − (T '1 −T '2 )
ln
T2
T1 − T2
T '1 −T '2
L
dove LMTD=MLDT (Media Logaritmica della Differenza di
Temperatura)
Quale ∆T scegliamo da inserire nell’equazione di Q?
Per tener conto del fatto che la differenza delle
temperature tra i due fluidi varia lungo la superficie di
scambio, ∆T utilizzato nell’espressione è un ∆T medio
logaritmico calcolato come segue
Controcorrente
∆TLMDT =
(T '1 −T2 ) − (T1 − T '2 )
ln
59
T '1 −T2
T1 − T '2
60
Esercizio
Un
fluido entra alla temperatura di 200°C ed esce alla
temperatura di 160°C, da uno scambiatore a tubi
concentrici, raffreddato da un altro liquido che entra alla
temperatura di 110°C ed esce alla temperatura di 150°C.
Calcolare il ∆TLMDT in equicorrente e in controcorrente
∆TLMDT =
(250 − 110) − (160 − 150) = 49.26°C
ln
∆TLMDT =
250 − 110
160 − 150
(160 − 110) − (250 − 150) = 72.13°C
ln
160 − 110
250 − 150
In controcorrente il ∆T è più elevato quindi posso utilizzare
tubi più corti a parità di calore scambiato
61