Magnetismo
naturale
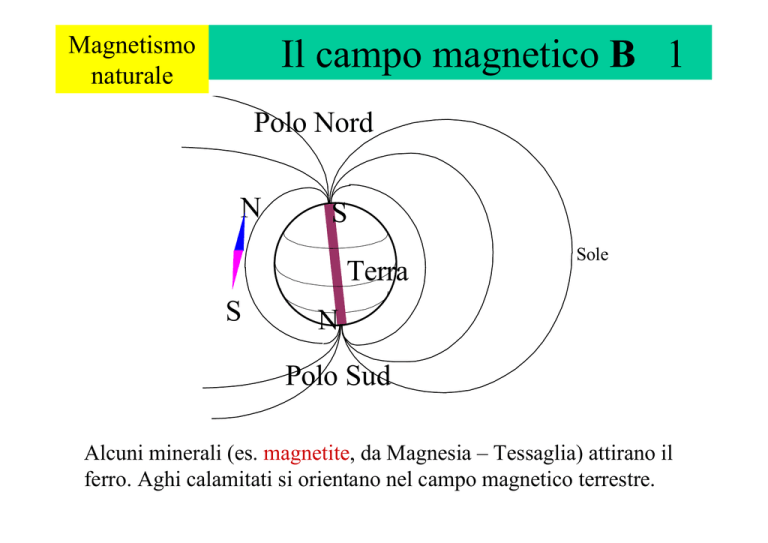
Il campo magnetico B 1
Polo Nord
N
S
Terra
S
Sole
N
Polo Sud
Alcuni minerali (es. magnetite, da Magnesia – Tessaglia) attirano il
ferro. Aghi calamitati si orientano nel campo magnetico terrestre.
Dipoli
magnetici
Il campo magnetico B 2
La Terra e le calamite sono dipoli magnetici, con proprietà simili a quelle
dei dipoli elettrici; poli opposti si attraggono e concordi si respingono; le
"linee di forza" escono dal polo nord ed entrano al sud
Il polo nord terrestre è il polo sud del dipolo magnetico terrestre
Direzione e verso di B sono indicati da un ago calamitato
II legge di
Laplace
Forza magnetica su corrente 3
Lo studio quantitativo del campo magnetico B comincia a partire dal
1800 grazie alle correnti continue prodotte dalla pila di Volta.
B produce una forza f su un tratto di
conduttore ∆l percorso da corrente I
(seconda legge di Laplace)
f = I ⋅ ∆l × B
Nord
I
∆l
B
Il campo magnetico B
("campo di induzione magnetica” )
è l'analogo di E (campo elettrico)
in quanto è il responsabile di
azioni di forza
Sud
f
r
a
Prodotto vettoriale
r r r
a = b ×c
r r
r
a perpend. a b e c
modulo a = b c sen θ
r r
se b ⊥ c ⇒ a = b c
r r
se b || c ⇒ a = 0
r
b
modulo F = I B sen θ ∆l
r
c
θ
r
F
Forza del campo B
r r
r
F = I ∆l × B
a è nella direzione di
avanzamento della vite
r θ
∆l
z
r
B
y
x
terna di assi cartesiani
ortogonali (x,y,z)
Convenzioni
sui segni
Forza magnetica su corrente 4
f
z
x
∆l
y
Sud
I
B
Nord
La forza è perpendicolare al piano individuato da ∆l e B
Un osservatore orientato piedi-testa come f deve ruotare ∆l
in senso antiorario di meno di 180° per sovrapporlo a B.
"regola della mano sinistra" = medio su ∆l, indice su B, pollice su f
Unità di
misura
Dimensioni di B
forza
Dimensioni di B =
corrente × lunghezza
newton
joule × s
unità di B (SI) =
=
=
2
ampere × metro coulomb × metro
volt × s weber
=
=
= tesla(T)
2
2
metro
metro
Si usa spesso il gauss = 10−4 tesla
5
I legge di
Laplace
Campo prodotto da corrente 6
Campo magnetico ∆B prodotto in
P da tratto ∆l di corrente I in O
(prima legge di Laplace ovvero
P
legge di Biot-Savart)
I
O
∆l
∆B
∆B = k m
∆l
I∆l × OP
OP
3
Per distribuzione di corrente J
J
∆S
∆B = k m
J × OP
OP
3
∆V con ∆V = ∆S ⋅ ∆l
Permeabilità
magnetica
La costante magnetica
Il valore di km è legato alla
scelta della unità di
corrente/carica
La costante magnetica si
esprime solitamente
mediante la permeabilità
magnetica del vuoto µ0
Il rapporto
costante elettrica /
costante magnetica
è indipendente dalla
scelta dell'unità
elettrica
7
[
[
l]
f ] [l ] [ f ]
−7 N
[k m ] = [B] =
⋅ = 2 = 10
[I ] [I ]× [l ] [I ] [I ]
A2
( )
µ 0 = 4πk m = 4π 10
−7
N
A2
µ0
km =
4π
N ⋅ m2
2
C m2
ke
1 4π
1
= 2 ≈
=
⋅
=
=
k m 4πε 0 µ 0 ε 0 µ 0 N s
C 2 / s2
( )
≈ 9 1016
m2
2
c
≈
s2
La forza su fili definisce completamente B
⇒
r r
r
F = I ∆ l × B ⇒ [F ] = [I ∆ l B ]
Forza
F
⇒
dimensioni
di
=
B
Corrente ⋅ Lunghezza
I
∆
l
[B ] =
Si definisce il Tesla,
unità di misura di B
1T =
1N
1 A ⋅1 m
Esempi: Elettromagnete B ≈ 2 T
Ferromagnete B ≈ 0.2 T
Campo magnetico terrestre ≈ 10-4 T
Si usa anche il Gauss: 1 Gauss = 10-4 T
Simbologia:
Campo entrante nel foglio
Campo uscente dal foglio
Forza totale su filo rettilineo in
campo magnetico uniforme e
perpendicolare al filo
r
F
B costante, θ = π/2, sen θ = 1
F diretta verso sinistra
F=
∫ dF = ∫ I B sen θ
filo
filo
dl = I B ∫ dl = I B L
filo
r
dl
L
I
direzione entrante nel piano
direzione uscente dal piano
Esempio: forza totale su un circuito
semicircolare in campo magnetico
uniforme, come in figura
r
B diretto come x
r raggio del semicerchio
Ir corrente
d l tratto di filo infinitesimo
θ angolo tra la direzione di
dl e quella di B
y
I
L
O
Forza sul tratto rettilineo:
direzione entrante nel piano
F1 = I L B
r
θ
dθ
θr
r
B
dl
r
F1
r
F2
0
Forza sul tratto semicircolare: direzione uscente dal piano;
dato che dl = r dθ e che l’angolo da da 0 a π percorrendo il semicerchio si ha
π
F2 =
x
∫ I B senθ dl = ∫ I B r senθ dθ = I B r [− cosθ ]0 = 2 I B r = I B L
semicerchio
π
0
uguale e opposta alla precedente. Quindi la forza totale è nulla.
Sarà possibile però un moto di rotazione (coppia di forze e momento meccanico)
B assiale
Spira di corrente
8
Campo lungo l'asse di una spira circolare di corrente
z
ϑ
y
x
dB(P)
Ids
r
r = R2 + z2
dBz
P(z)
ϑ
cos ϑ =
dϕ O
R
=
r
R
R2 + z2
R
µ0 I Rdϕ ⋅ r
cos ϑ =
dBz = dB( P) ⋅ cos ϑ =
3
4π
r
=
µ0 I Rdϕ
4π R 2 + z 2
R
R2 + z 2
=
µ0 IR
4π
2
dϕ
3
( R +z )
2
2
Bz =
(
µ 0 IR 2
2
2 R +z
2
)
3
Dipolo
magnetico
Spira: momento magnetico 9
Il campo al centro della spira è inversamente proporzionale al raggio R
µ0 I
z =0
→ =
2
µ 0 IR
2R
Bz =
⇒
2
3
µ 0 m mag
µ
I
π
R
z >> R
2
2
0
→ ≈
=
2 R +z
3
2πz
2πz 3
(
)
( )
A grande distanza dalla spira il campo magnetico è inversamente proporzionale al cubo della distanza (z) dal centro della spira e direttamente
proporzionale al prodotto della corrente (I) per l’area della spira (πR2).
(
corrente × area spira ≡ momento magnetico mmag
)
Dipolo elettrico e dipolo magnetico si estinguono con il reciproco del
cubo della distanza
Confronto
con dipolo
elettrico
Dipolo magnetico 10
Dipolo elettrico e dipolo magnetico sono differenti
Le linee di forza
elettriche escono
dalle cariche
positive ed entrano
in quelle negative
N
E
B
S
Manca l'equivalente di "carica"
localizzata nel caso magnetico: le linee di
forza sono continue attraverso il dipolo.
Formula di
Biot-Savart
Filo percorso da corrente 11
Campo in punto P a distanza R da un filo indefinito percorso da
corrente I
dz
z + dz
dz×r
z
I
dϑ
r
P
R
dB(P)
ϑ
O
P
R
O
µ 0 I ∞ r cosϑdz
=
B( P) =
∫
3
4π −∞ r
π /2
µ0 I
cosϑ dϑ µ 0 I
=
=
∫
4π −π / 2
R
2πR
R
cosϑ
z = R tan ϑ
dϑ
dz = R
cos 2 ϑ
r=
Regola della
mano destra
Filo percorso da corrente 12
Le linee di forza di B sono cerchi concentrici attorno al filo e vale la
"regola della mano destra"
B ∝1/distanza
I
O
Pollice nel verso della
corrente ⇐⇒ le dita
chiuse seguono B
∆l
B ∝ ∆l × OP
P
B solenoidale
La divergenza di B è nulla 13
Le linee di B prodotte dal filo indefinito sono
anelli chiusi ⇒ B è un campo solenoidale,
ossia a divergenza nulla
Il risultato è subito dimostrabile
per fili indefiniti normali al
piano del disegno, ma è vero in
generale come conseguenza
formale della legge di Laplace.
∫ B ⋅ ndS = 0
S
∇⋅B = 0
B
Qualunque siano le correnti, le linee di B sono sempre chiuse
(mancano sorgenti o pozzi)
Il caso del filo
indefinito
La circuitazione di B
14
La circuitazione di B prodotto da filo indefinito
percorso da corrente lungo linea chiusa
appartenente al pino del disegno normale al filo ≡
≡ lavoro di B lungo una linea chiusa e orientata C
C
B
dϕ
dl
R
2π
µ0 I
∫ B ⋅ dl = ∫ 2πR Rdϕ =µ0 I
C
0
La circuitazione di B è indipendente da R !!!
Corrente concatenata
Il risultato vale per qualunque
linea chiusa che concatena la
corrente. Il contributo di un tratto
di C dipende solo dall’angolo dϕ
sotto cui è vista da I
∫ B ⋅ dl =
C
2π
∫
0
µ0 I
⋅ Rdϕ = µ0 I
2πR
R
dϕ
C
Se C non concatena la
corrente la circuitazione di B
è nulla. L'integrale da A a B
(lungo il verso positivo di C)
è proporzionale a ϕ0, quello
da B ad A a −ϕ0.
B
dl
B
B
B
dϕ
ϕ
15
dl
dl'
ϕ0
A
Fili di
corrente
Teorema di Ampère
La circuitazione di B lungo
una linea chiusa C è uguale a
µ0 per la somma delle
correnti concatenate con C
16
I
∫ B ⋅ dl = µ0 ∑c IC
'
C
C
I3
I1
C
I3
I4
I2
∑'C I c = I 1 − I 2
Densità di
corrente
Teorema di Ampère
17
Nel caso di correnti non filiformi di densità J, la corrente
concatenata è pari al flusso di J su una qualunque superficie
appoggiata su C e orientata secondo la regola della mano destra
(dita lungo verso positivo di C, pollice nella direzione positiva della
normale ad S)
∫ B ⋅ dl = µ0 ∫ J ⋅ ndS
C
J
S
n
J
S
dl
J
n
C
B
J
Teorema del
rotore
Circuitazione e rotore 18
dy
dx
dy
dx
∫ B ⋅ dl = B y 2 dy − Bx 2 dx − B y − 2 dy + Bx − 2 dy =
C
dy
dx
dy
dx
= B y − B y − dy − B x − B x − dx =
2
2
2
2
B(0,dy/2)
∂B y
∂B y ∂B x
∂B x
dS = (∇ × B ) ⋅ kdS
dxdy −
dydx =
=
−
x
y
∂x
∂y
∂
∂
La circuitazione lungo un quadrato
elementare nel piano xy è uguale al
B(−dx/2,0)
flusso del rotore attraverso la
y
superficie del quadrato. La somma
delle circuitazioni su quadrati
x
adiacenti è pari alla somma dei
flussi e alla circuitazione sul
perimetro complessivo.
B(dx/2,0)
B(0,−dy/2)
Forme integrale e puntuale
Circuitazione e rotore 19
La circuitazione di B lungo una linea chiusa qualunque C è sempre uguale al flusso di rotB su S a contorno C ; per il teorema di Ampère tale
circuitazione è pari al flusso per S della densità di corrente (concatenata)
∫ B ⋅ dl ≡ ∫ (∇ × B ) ⋅ n dS =µ 0 ∫ J ⋅ ndS
C
S
Il teorema di Ampère vale se e solo se gli
integrandi degli integrali su S sono uguali
(forma puntuale del teorema di Ampère)
S
rot B ≡ ∇ × B = µ 0 J
NB. Perché l'integrale di J su S dipenda
solo dal contorno C di S è necessario che ∇ ⋅ J = 0
Il rotore di un qualunque vettore è sempre
div(rot B ) ≡ ∇ ⋅ ∇ × B = 0
solenoidale
Definizione
Il rotore
20
Il rotore in coordinate cartesiane si esprime mediante lo sviluppo di
una matrice 3×3, in modo analogo al prodotto vettoriale
i
∂
∇×B ≡
∂x
Bx
∂
= ∂y
By
∂
∂
∂z i − ∂x
Bx
Bz
j
∂
∂y
By
k
∂
=
∂z
Bz
∂
∂
∂z j + ∂x
Bz
Bx
∂
∂y k =
By
∂B z ∂B y ∂B x ∂B z ∂B y ∂B x
k
i +
−
=
−
−
j +
∂
∂
∂
∂
y
z
z
x
x
y
∂
∂
Cavo pieno
Applicazioni
J
1
Cavo conduttore cilindrico di raggio R e corrente
continua complessiva I0
∫ B ⋅ ds = B ⋅ 2π d = µ 0 I (d )
B
µ 0 I (d )
⇒B=
2πd
2
B
con
B
µ0 I 0
2πR
0
21
R
2R
d2
d < R ⇒ I (d ) = 2 I 0
R
d > R ⇒ I (d ) = I 0
µ0 I 0
d < R ⇒ B(d ) =
d (caso1)
2
2πR
µ0 I 0
d > R ⇒ I (d ) =
(caso2)
2πd
d
Corrente su
lastra
Applicazioni
22
La lastra indefinita di corrente con densità J e spessore s
B
C
l
z
s
y
J
J
x
B
2lB = µ 0 ( slJ ) ⇒ B =
µ 0 sJ
2
B è costante per distanze dalla lastra piccole rispetto
alla sua dimensione
Solenoide
Applicazioni
23
Solenoide indefinito con n spire di corrente I in un tratto L. Solo il campo
interno contribuisce alla circuitazione perché molto maggiore di quello
esterno. Il campo del solenoide infinito è omogeneo
Bext ~ 0
Bint l = µ 0 (nI )
I
B
⇓
Bint =
H=
µ0 ⋅ I ⋅ n
⇓
B
µ0
B
l
=I
n
l
l
Forze tra correnti parallele 24
Forze tra fili percorsi da correnti
I1
∆l1
B2
f12 = I1∆l1 × B 2 =
I2
f21
f12
B1
O
P
µ 0 I1I 2
∆l1
2π r
B2
z
y
r
L’ampere di corrente è stato
definito grazie alle forze su fili
x
correnti equiverse si attirano
correnti opposte si respingono
Momento di f
La spira di corrente è libera
di ruotare lungo il suo asse
parallelo ad x ( i) in un
campo B uniforme
forza su lato lungo a
f a = IaBj
momento delle forze fa e −fa
M = − IabB sin ϑ i
Forze su spira
25
B
fb
n
ϑ
fa
a
− fa
b
z
I
− fb
y
x
Il momento delle forze fb è nullo poiché le forze hanno la stessa retta
d'azione (braccio nullo)
Potenziale
della spira
Energia della spira in B
26
Il momento magnetico della spira rettangolare della figura precedente è
m mag = Iabn = Iab(cos ϑ ⋅ k − sin ϑ ⋅ j)
i
j
Definizione generale del
momento delle forze → M = m mag × B = 0 − Iab sin ϑ
agenti su spira
0
0
espressione precedente →
E p = −m mag ⋅ B = −(Iab )B cos ϑ
k
Iab cos ϑ =
B
= − IabB sin ϑi
Energia potenziale di un dipolo
ϑ
ϑ
90°
90°
E p = − ∫ M x dϑ ' = (Iab )B ∫ sin ϑ ' dϑ ' = −(Iab )B cos ϑ
L’energia potenziale del dipolo magnetico è il lavoro del momento
cambiato di segno
Momento meccanico su una spira
θ
Vista di fronte
r
B
r
F1
Ir
F1
z
r
F1
Vista dall’alto
r
F2
x
r
B
Spira rettangolare di superficie S = a b,
con corrente I, immersa in campo
magnetico uniforme B diretto come x
Forze sui tratti diretti come x
(paralleli a B) : nulle
Forze sui tratti diretti come z
(perpendicolari a B) : F1 = F2 = I B b
Corrente entrante nel foglio
Corrente uscente dal foglio
Angolo tra B e la normale
alla superficie della spira
r
n
θ
r
B
y
r
F2
x
r
F2
F1 e F2 hanno direzioni opposte ⇒ coppia di forze
moto rotatorio intorno al punto centrale O
momento meccanico rispetto a O:
a
a
a
M = F1 sen θ + F2 sen θ = 2 ⋅ IbB sen θ =
2
2
2
⇒ M = I ⋅ S ⋅ B ⋅ sen θ
Momento meccanico = corrente · superficie · campo
θ =π
r
n o
r
B
r
n
[M] = [I ⋅ S ⋅ B] = Am2 T = Am2
θ =π /2
r
B
Momento meccanico zero
(posizione di equilibrio instabile)
energia massima U = + I S B
o
N
= Nm
Am
θ = 0r
n
Momento meccanico zero
(posizione di equilibrio stabile)
energia minima U = - I S B
Momento meccanico massimo
energia zero
M =ISB
U =0
Energia della spira nel campo magnetico: U = − I S B cos θ
(N.B la normale n alla spira
corrisponde alla regola del
cacciavite ruotando secondo la
rotazione della corrente)
(si ricava calcolando il lavoro meccanico per la rotazione della spira)
Motori elettrici: si ottiene lavoro meccanico sfruttando il movimento della spira nel
campo di induzione magnetica, variando nel tempo sinusoidalmente la corrente per
mantenere momento meccanico e rotazione (motori sincroni)












