1
Vita di una stella come il sole.
(in pillole)
2 dritte sulla luce.
La luce può essere pensata come un’onda
elettromagnetica che si propaga nello spazio (anche nel
vuoto!) alla incredibile velocità di circa 300 000 km/s. I
parametri essenziali che determinano la luce sono la sua
velocità di propagazione, che indichiamo con la lettera
c, la lunghezza d’onda (lambda) e la frequenza (nu)
dell’onda elettromagnetica.
B
A
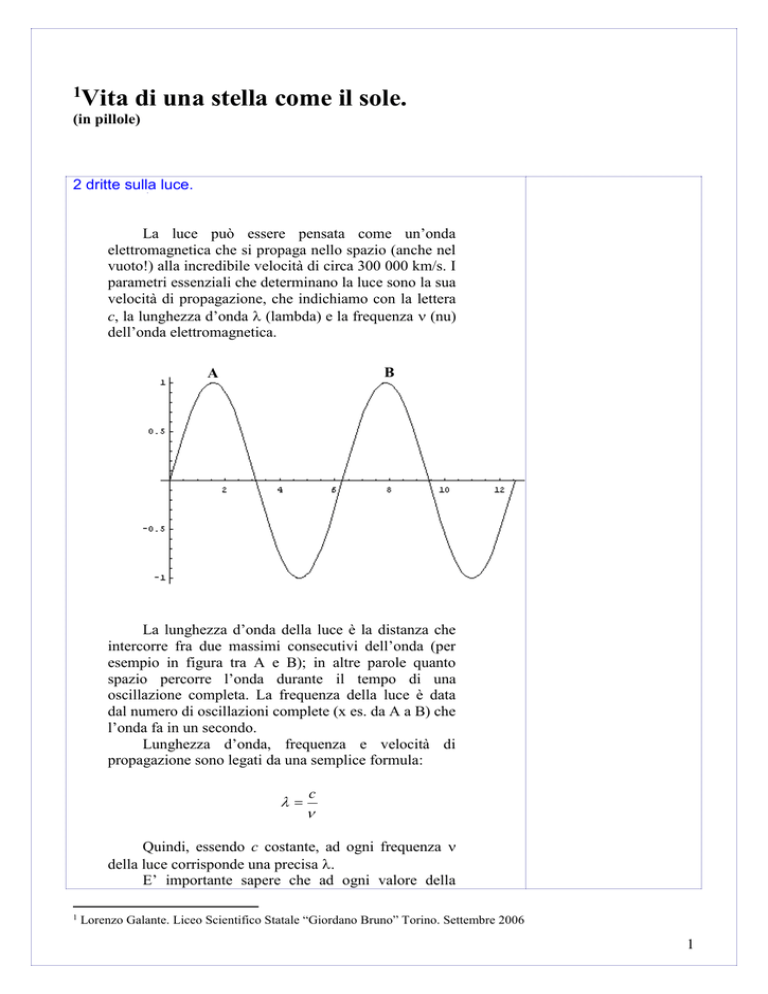
La lunghezza d’onda della luce è la distanza che
intercorre fra due massimi consecutivi dell’onda (per
esempio in figura tra A e B); in altre parole quanto
spazio percorre l’onda durante il tempo di una
oscillazione completa. La frequenza della luce è data
dal numero di oscillazioni complete (x es. da A a B) che
l’onda fa in un secondo.
Lunghezza d’onda, frequenza e velocità di
propagazione sono legati da una semplice formula:
c
Quindi, essendo c costante, ad ogni frequenza
della luce corrisponde una precisa .
E’ importante sapere che ad ogni valore della
1
Lorenzo Galante. Liceo Scientifico Statale “Giordano Bruno” Torino. Settembre 2006
1
frequenza della luce corrisponde un ben determinato
‘colore’ della luce stessa. Per esempio il rosso ha una
frequenza più bassa del blu e il blu più bassa del
violetto. Attenzione però. Non tutti i ‘colori’ della luce
sono percepibili dai nostri occhi. Noi vediamo dal rosso
al violetto (tutti i colori dell’arcobaleno) ma prima del
rosso abbiamo gli infrarossi, le micro-onde, le onde
radio, dopo il violetto abbiamo l’ultravioletto i raggi x e
raggi gamma. Tutti questi ‘colori’ non sono percepiti
dai nostri occhi, ma possono essere percepiti costruendo
degli ‘occhi artificiali: le antenne. Questo è molto
importante perché oggi osserviamo l’universo non solo
nel visibile, ma anche in tutte le altre frequenze e
sappiamo che esistono molti oggetti che non emettono
nel visibile che sono delle fortissime sorgenti di luce
(giove per esempio è una radio sorgente molto forte e
può essere percepito con un’opportuna antenna che
abbiamo costruito nel nostro liceo e che dovrebbe
essere più utilizzata e migliorata – chi ha voglia di
lavorarci si faccia avanti).
La nascita di una stella.
Le stelle nascono da immense nuvole di idrogeno
presenti nello spazio (Nebulose). In queste nuvole ci
possono essere zone in cui è più alta la concentrazione
di H e dunque più grande la massa presente. Visto che
la quantità di massa determina l’intensità delle forze
gravitazionali, tali zone sono veri e propri centri di
attrazione che richiamano verso di loro tutti gli atomi di
idrogeno nelle vicinanze. In tal modo sempre più
idrogeno da tutte le direzioni si addensa verso un punto:
è iniziata la formazione di una palla di gas di H che si
chiamerà stella. Con il passare del tempo gli strati più
interni di questa palla (all’interno dei quali sempre più
H si concentra) raggiungono pressioni e temperature
elevatissime (si parla di milioni di gradi)
La pressione di un gas
aumenta quando in un
certo volume si concentra
sempre più gas. Lo stesso
capita nel centro di una
stella che si sta formando.
Aumentando la pressione
aumenta anche la
temperatura del gas (vedi
gonfiaggio ruota bici o
pentola a pressione)
2
Al centro del Sole
avvengono reazioni nucleari di fusione
Al centro di una stella come il Sole la temperatura
è di circa 15 milioni di gradi e la pressione è circa 300
miliardi di volte maggiore della pressione atmosferica
terrestre. Ciò fa sì che gli atomi siano spogliati dei loro
elettroni. Il centro della stella è composto da nuclei
(neutroni n e protoni p legati fra loro) ed elettroni liberi.
La temperatura di un gas è strettamente legata alla
velocità con cui si muovono le sue particelle, quindi i
nuclei presenti al centro di una stella si muovono a gran
velocità e quando urtano possono arrivare quasi a
toccarsi superando la repulsione elettrostatica (i nuclei
sono carichi dello stesso segno – positivo – quindi
tendono a respingersi). Quando ciò accade può
verificarsi il processo di fusione che libera l’energia che
tiene accesa la nostra stella.
Alta temperatura di un gas
= alta velocità delle sue
particelle.
I nuclei si respingono
perché tutti carichi
positivamente.
Le reazioni di fusione
avvengono solo perché nel
sole i nuclei urtano ad una
velocità tale da farli
avvicinare molto
3
La reazione di fusione termo-nucelare
La chiave di volta del processo di fusione sta
nell’equivalenza massa-energia (Einstein 1905, teoria della
relatività ristretta). In accordo con le idee di Einstein una
certa quantità di massa m può essere convertita in energia E
rispettando la famosa relazione
E mc 2
Dove c è la velocità della luce = 3 10 m / s . Nel nucleo del
Sole 4 nuclei di H (cioè 4 protoni ‘p’) si uniscono a
formare un nucleo di He (2 protoni e 2 neutroni ‘n’):
8
4 H He energia
Durante questa reazione 2 dei 4 p si trasformano in n,
liberando positroni ‘e+’ e neutrini ‘’. Il processo di
trasformazione di un p in un n è schematizzato così
I positroni e+ sono le
particelle di antimateria
corriposndenti
all’elettrone e- (hanno
cioè la stella massa
dell’elettrone, stessa
carica ma di segno
opposto.
Il neutrino è una
particella dotata di
massa pressoché nulla
e priva di carica. Il sole
invia verso la terra
numerosi neutrini in
grado di attraversare
l’interno pianeta senza
entrare in ‘contatto’ con
alcunché.
p n e
Durante il processo di fusione un po’ di massa va persa:
l’elio ha una massa lievemente inferiore a quella dei 4H:
massa di 4 H 6.693 10 27 kg
massa di 1He 6.645 10 27 kg
massa perduta 0.048 10 27 kg
La massa perduta (circa lo 0.7%) è convertita in energia
secondo la formula
E mc 2 0.048 10 27 kg 3 108 m / s 4.3 10 12 joule
2
Così se pensiamo alla conversione di 1kg di H in He
abbiamo una massa mancante di 0.007 kg corrispondente a
6.3 1014 joule (energia pari a quella ottenuta in una centrale
a carbone bruciando 20 milioni di kg di carbone).
4
Quanti kg di H ‘brucia’ in un secondo?
Il Sole irradia nello spazio circa 3.9 1026 joule/s.
Puoi calcolare quanti kg di H brucia in un secondo?
Dal box precedente sai
quanti joule vengono
liberati da 1 kg di H…
Risposta:___________________________ .
In ogni caso possiamo stare tranquilli la massa del Sole
è di circa 2 1030 kg
La luminosità di una stella
Le stelle emettono luce in maniera molto simile
ad un corpo nero. Possiamo immaginare un corpo nero
come una scatola con pareti opache dotata di un piccolo
forellino, dal forellino può entrare luce di qualsiasi
colore o frequenza. La luce una volta entrata viene
assorbita e riemessa in continuazione dalle pareti
interne della scatola, ma la probabilità che essa ha di
uscire dal forellino è pressoché nulla, il forellino appare
allora nero (ecco perché l’apertura di una lattina di coca
cola appare nera). Detto questo se andassimo ad
esaminare quanta luce è presente all’interno della
scatola vedremo che la risposta dipende dalla
temperatura T a cui la scatola si trova e vedremo che
l’energia F luminosa che attraversa una superficie
unitaria nell’unità di tempo va con la quarta potenza
della temperatura stessa (legge di Stefan-Boltzmann):
F T
4
dove è una costante.
E’ un fatto sperimentale che per le stelle valga a grandi
linee la stessa legge valevole per i corpi neri: esse
irradiano rispettando la legge di St-B. Allora la
luminosità L di una stella (cioè la quantità di energia
luminosa emessa nell’unità di tempo: potenza) si può
esprimere come prodotto della superficie della stella e
di F
La legge di St.-B spiega per
esempio perché vediamo le
macchie solari nere (sono
zone della fotosfera a più
bassa temperatura e quindi
emettono meno luce delle
zone circostanti, per
contrasto le vediamo nere.
Allo stesso modo vediamo
nero un volto di un persona
controluce e bianco lo
sfondo. Sapendo che la
temperatura delle macchie
è di 4300 K mentre altrove
la temperatura è di 5800 K.
Sapresti calcolare qual è la
percentuale di luce irradiata
dalla macchie rispetto alle
zone circostanti?
La legge di St.-B. ci spiega
anche perché è possibile
osservare ad occhio nudo
delle giganti rosse come
Aldebaran e Arturo (lo
vedremo più avanti).
Luminosità L di una stella:
quanta energia luminosa
irradia nell’unità di tempo.
E’ una potenza.
[dimensioni: Joule/s=Watt]
L 4R 2T 4
Dove R è il raggio della stella e T la temperatura
superficiale.
5
Si vede bene che la luminosità di una stella dipende da
2 fattori: la sua temperatura superficiale (T) e le sue
dimensioni (R).
Calcolo della temperatura superficiale del Sole.
Sappiamo che il Sole investe 1m2 della superficie
terrestre con circa 1370 Joule al secondo. In altri
termini l’irraggiamento del sole sulla terra è di 1370
W/m2. Tale valore prende il nome di costante solare.
Se questa potenza è moltiplicata per la superficie di una
sfera immaginaria centrata nel sole e con raggio pari
alla distanza terra-sole RT-S, si ottiene la potenza del
sole (o luminosità L), cioè quanti sono i watt di una
lampadina che potrebbe sostituire la nostra stella.
W
4 R 2 T S
2
m
W
L 1370 2 4 (1.5 1011 m) 2 1.37 4 2.25 10 25 W
m
38.7 10 25 W
L 1370
Il Sole equivale ad una
lampadina da circa 400
milioni di miliardi di miliardi
di Watt!
Dalla luminosità L del Sole possiamo risalire alla F del
Sole ricordando che L F Superfice stella , quindi:
F
L
38.7 10 25W
W
0.0628 10 9 2
2
2
4RS 4 7 108 m
m
Ma F è anche dato dalla legge di St.-B., per cui
0.0628 10 9
W
T 4
2
m
e da questa relazione possiamo ricavare la temperatura
superficiale del sole:
T 4
Il raggio del Sole è pari a
7 105 km
5.67 10-8 Wm-2K-4
0.0628 10 9 Wm 2
4 0.011 1017 5770 K
5.67 10 8 Wm 2 K 4
6
Il Sole diventerà una gigante rossa.
brucia He
Quando l’H si è esaurito a furia di trasformarsi in
He, la stella termina la fase tranquilla della sua vita
(esce dalla sequenza principale): arriva l’epoca delle
grandi
trasformazioni.
Le
reazioni
nucleari
diminuiscono sensibilmente, la gravità ha la meglio, la
stella ora formata da un nucleo di He e un inviluppo di
H, collassa sotto il proprio peso. Pressione, densità e
temperatura aumentano. In tal modo l’H degli strati
esterni inizia a dar vita a reazioni di fusione
termonucleare, gli strati più esterni allora iniziano a
espandersi. Il nucleo di He, invece, continua a
collassare. Quando il nucleo della stella arriva a 100
milioni di gradi, anche l’He dà vita reazioni di fusione
nucleare: a 3 a 3 i nuclei di He ‘fondono’ dando vita al
Carbonio (C), il C fonde con un altro nucleo di He
generando Ossigeno (O). Tutto questo avviene in
qualche centinaio di milioni di anni, dopodichè la stella
ritrova pace: l’He ‘brucia’ al centro, l’idrogeno negli
strati più esterni. Intanto la stella è diventata enorme (il
volume è aumentato di un miliardo di volte), la sua
superficie è così lontana dal nucleo ove avvengono le
reazioni nucleari da avere una temperatura molto più
bassa, appare dunque rossa. La stella è diventata una
gigante rossa. Betelgeuse, Aldebaran, Arturo sono
tutte giganti rosse ben osservabili nel nostro cielo. Esse
sono molto luminose grazie alla loro incredibile
estensione superficiale (vedi paragrafo Luminosità di
una stella per una spiegazione più dettagliata). Fra circa
5 miliardi di anni anche il nostro sole diventerà una
gigante rossa inglobando al suo interno anche l’orbita
terrestre.
brucia H
IL fatto che il colore di una
stella dipenda dalla
temperatura è dovuto alla
Legge di Wien – vedi più
avanti.
Giganti rosse … la storia non è finita.
La fusione dell’elio (He) nel nucleo di una gigante
rossa produce carbone (C) e ossigeno (O). Per una stella
come il nostro sole essa andrà avanti per circa 100
milioni di anni. Al termine di questo periodo tutto l’elio
del nucleo sarà convertito in C ed O e la fusione
dell’He cesserà. Senza fusioni termonucleari per
mantenere la pressione interna del nucleo, esso si
contrarrà fino a quando interverrà la pressione di
degenerazione degli elettroni. Vediamo in cosa consiste
7
questa pressione dal nome così strano che fa si che il
nucleo della gigante rossa non si contragga fino a
diventare un punto. Nel nucleo di una gigante rossa la
temperatura è così alta che e- e nuclei, prima legati a
formare atomi, sono liberi. Abbiamo quindi un mare di
e- e nuclei separati. Per gli e- vale il Principio di
Esclusione di Pauli, che in sostanza afferma che due enon possono occupare lo stesso stato quantistico. Ecco
perché lungo ogni orbita degli elettroni intorno al
nucleo troviamo al massimo 2 e- che la occupino
contemporaneamente. Allora non tutti gli elettroni di un
atomo possono stare contemporaneamente sull’orbita
più vicina al nucleo: 2 possono starci, gli altri vanno
distribuiti a 2 a 2 lungo le orbite più esterne. Ciò fa si
che l’atomo non possa essere compresso e non si possa
farlo diventare più piccolo a causa di una sorta di
pressione quantistica dovuta al principio di esclusione.
Qualcosa di molto simile capita al mare di e- confinati
nel nucleo della gigante rossa alla fine della fase delle
reazioni ad He.
La contrazione del nucleo, arrestata dalla
pressione degenere degli elettroni, produce una gran
dose di calore che surriscalda gli strati di He circostanti
il nucleo stesso. In tal modo si innescano le reazioni di
fusione dell’He negli strati a contatto con il nucleo
ormai spento. Siamo in una seconda fase di gigante
rossa detta AGB (Asymptotic Giant Branch). A questo
punto la stella è formata da un nucleo inerte e degenere
di C ed O, circondato da uno strato di He che brucia,
avvolto a sua volta in uno strato di H che brucia; il tutto
in un volume confrontabile con quello della Terra.
Questa piccola e densa regione centrale è circondata da
un inviluppo di H dalle dimensioni dell’orbita di Marte.
Da Gigante Rossa a Nebulosa Planetaria.
Durante la fase AGB la stella si appresta a morire.
Essa espelle nello spazio tutti i suoi strati esterni al
nucleo. Alla fine dunque la stella diventa una nebulosa
planetaria cioè un nucleo ad alta temperatura
circondato dai materiali espulsi. Con un telescopio
amatoriale si può osservare nella costellazione della
Lira un esempio di nebulosa planetaria: la Ring
Nebula. Essa ci mostra ciò che diventerà il nostro sole
fra molto tempo. La si osserva come un anello di gas
che circonda una puntino luminoso (il nucleo anche
detto nana bianca). Per osservare il puntino luminoso
8
però occorrono telescopi con generose aperture. Il
perché accada questo è piuttosto complesso e direi di
lasciarlo stare. Chi volesse saperlo me lo può dire e
possiamo parlarne.
La legge di Wien
La temperatura superficiale di un corpo è legata al
colore della luce che emette. Una sbarra di metallo alla
temperatura di 20 °C emette luce infrarossa (e infatti
noi non lo vediamo emettere luce, solo riflettere quella
già presente), se la scaldiamo oltre un certo limite
emette luce rossa, se si va ancora oltre, luce bianca. Va
detto che la sbarretta di metallo del nostro esempio, ad
una certa temperatura, non emette luce di un solo
colore, ma emette luce di tutti i colori possibili. Allora
quando diciamo che la sbarra emette luce rossa se è
incandescente intendiamo che emette luce rossa con
intensità molto più alta rispetto a tutti gli altri colori.
Esiste una legge che specifica il legame tra la
temperatura di un oggetto e il colore della luce emessa
con la massima intensità: la legge di Wien,
0.0029
,
T
dove MAX indica la lunghezza d’onda del colore più
emesso da un oggetto e T la sua temperatura espressa in
gradi kelvin.
MAX
Si capisce che tale legge è molto importante perché
permette di stabilire la temperatura superficiale di un
corpo misurando la lunghezza d’onda max emessa dal
corpo stesso. Se avessimo a disposizione un dispositivo
per misurare l’intensità della radiazione emessa dal sole
lunghezza d’onda per lunghezza d’onda potremmo
calcolare facilmente la sua temperatura superficiale.
Esempio: Sirio la stella più
luminosa del cielo
notturno ha una
temperatura superficiale di
10000 K. Possiamo usare
la legge di Wien per
determinare quale sia il
‘colore’ più emesso da
Sirio.
Provate a fare il calcolo e
determinate in quale banda
di colore Sirio emette
maggiormente
(…da 10 nm a 400nm
abbiamo la banda
dell’ultravioletto, tra 400nm
–viola- e 700 nm -rossoabbiamo la luce visibile, da
700 nm a 1mm
l’infrarosso…)
9
Convezione Irraggiamento e Conduzione nelle stelle
Nel centro del Sole, dove avvengono le reazioni
termonucleari, viene prodotto un grande ammontare di
energia. Se questa non fosse trasportata dal centro verso
l’esterno e diffusa nello spazio circostante il Sole
aumenterebbe la sua temperatura a dismisura. Ciò non
avviene, significa quindi che il l’energia viene
trasportata verso l’esterno. Esistono 3 modi per
trasportare energia da un posto all’altro: la conduzione,
la convezione, l’irraggiamento. La conduzione, ad
esempio, fa sì che se scaldiamo una sbarra metallica ad
un estremo, dopo un po’ di tempo anche l’altro diventi
caldo (questo è possibile grazie agli urti tra gli atomi
del metallo; i più caldi e più veloci urtano con i vicini
freddi, cedono loro energia e li riscaldano…). I moti
convettivi si verificano quando un fluido viene scaldato
dal basso in presenza di un campo gravitazionale (essi
sfruttano il moto verso l’alto di masse di fluido caldo
che cedono calore al fluido più in alto, si raffreddano e
ridiscendono,
innescando
così
moti
ciclici).
L’irraggiamento è il trasporto di energia ad opera della
luce, la brace ad esempio si raffredda inviando nello
spazio luce rossa. Nel sole la conduzione non avviene:
il motivo risiede nel fatto che il sole è una palla di gas
poco densa, anche nel nucleo dove la densità è
maggiore. Bassa densità implica lontananza tra le
particelle che costituiscono la stella, dunque bassa
possibilità di colpirsi e scambiare energia. Restano
l’irraggiamento e la convezione. L’irraggiamento
predomina dove la luce può fare lunghi tragitti senza
essere assorbita. Per il primo 70% del raggio solare a
partire dal centro avviene proprio questo e l’energia
viene
trasportata
verso
l’esterno
tramite
l’irraggiamento. Ma oltre questa distanza la temperatura
si è così abbassata da consentire il ricombinarsi di e- e
p+ a formare atomi di H. Gli atomi di H sono molto più
efficienti nell’assorbire la luce di quanto non fossero
elettroni e protoni separati, quindi da lì in avanti la luce
non ce la fa a portare via energia con sufficiente
velocità. Lì si ha quindi un aumento di temperatura e
diventano dominanti i moti convettivi. I moti convettivi
si dispongono lungo celle che emergono sulla fotosfera
e sono osservabili da terra con un telescopio come
piccoli puntini sulla superficie del sole. Tali celle
conferiscono un aspetto detto granulare alla superficie
della fotosfera. Nelle belle giornate di sole noi avremo
il compito di far notare questo aspetto a chi verrà a
trovarci! Tra l’altro abbiamo un bel esperimento sui
moti convettivi.
10
Cosa accade alle stelle più massicce del Sole.
Stelle più massicce del sole producono elementi pesanti nel loro
nucleo.
Nelle stelle con massa fino a 4 volte la massa solare nel
nucleo si innescano solo 2 tipi di reazioni
termonucleari: quelle dell’H e quelle dell’He. Gli
elementi più pesanti prodotti da tali stelle sono quindi il
C e l’O. Le stelle con masse > di 4 masse solari invece
possono innescare reazioni nucleari di C, O e di altri
elementi ancora più pesanti. La ragione è molto
semplice: maggior massa implica maggior forza di
gravità e quindi maggior pressione e temperatura nei
loro centri. Temperatura tali da far bruciare anche
elementi molto più pesanti dell’He. Sono queste le
stelle che hanno formato gli elementi ora presenti sulla
terra. Esse, infatti, nelle ultime fasi della loro vita
espellono materiale verso l’esterno mettendolo a
disposizione di future generazioni di stelle o pianeti.
Nelle stelle motlo massicce
la forza di gravità riesce a
vincere la pressione di
degenerazione degli
elettroni che, invece,
arrestava la contrazione
del nucleo nelle stelle
come il Sole, fermandole
ad un nucleo di C e O.
Esplosioni di Supernova.
Nel nucleo di una stella molto massiccia si può
arrivare ad innescare reazioni termonucleari del ferro
(Fe), ma oltre non è possibile andare. Quando si arriva
ad un nucleo di Fe, le reazioni nucleari si interrompono,
ha quindi la meglio la gravità che contrae rapidamente
il nucleo, la temperatura passa rapidamente a 5 miliardi
di k (5 x 109 k) e la luce emessa da un corpo nero a
questa temperatura è luce gamma: raggi gamma. Luce
con energia molto alta. In poco tempo il nucleo diventa
così denso che e- e p+ sono così vicini da essere forzati
a produrre particelle neutre: i neutroni (n):
e p n .
I neutrini sfuggono al nucleo della stella e gli rubano
così un grande ammontare di energia; il nucleo si
raffredda e si addensa ancor di più. Il nucleo arriva a
dimensioni di 20 km e densità pari a 4 1017 kg/m3 (400
milioni di miliardi di kg al metro cubo!). Queste sono le
densità del nucleo, cioè le densità con cui p+ e n sono
avvicinati nei nuclei atomici. Raggiunta questa densità
11
il nucleo non può più contrarsi, allora la contrazione in
atto subisce un brusco stop e buona parte del nucleo che
si stava contraendo rimbalza all’indietro generando una
gigantesca onda di pressione verso l’esterno. E’ da
questa gigantesca onda di pressione che nasce un
rilascio di energia incomprensibilmente alto da parte
della stella: la stella è diventata una supernova.
Quando una stella molto massiccia diventa supernova,
essa da debole stella del cielo notturno può diventare
così luminosa da essere visibile ad occhio nudo di
giorno. Durante la fase di supernova l’onda d’urto
titanica, che porta al tremendo rilascio di energia, forma
elementi ancora più pesanti del Fe (si arriva fino
al’Uranio). Possiamo allora concludere che gran parte
del materiale presente sul nostro pianeta e anche dentro
i nostri corpi, molto tempo fa, apparteneva ad una stella
che nacque, visse e … morì come una supernova.
Stelle di neutroni.
Quando nel nucleo di una stella molto massiccia
l’enorme pressione spinge e- e p+ ad unirsi in un n si
viene a formare una stella di neutroni. La pressione di
degenerazioni dei neutroni (molto maggiore di quella
degli elettroni) non consente ulteriori contrazioni del
nucleo ad opera della gravità.
La scoperta delle Pulsar.
Intorno al 1960 Jocelyn Bell lavorò a lungo per aiutare
a costruire un array di radio antenne (lo tradurrei una
serie di antenne disposte le une di seguito alle altre) in
Inghilterra. Lo strumento fu completato nel 1967, e Bell
e i suoi colleghi iniziarono ad utilizzarlo per scrutare le
radio emissioni provenienti dal cielo. Bell notò che le
antenne avevano rilevato un disturbo radio pulsante
proveniente da una particolare regione del cielo. Le
pulsazioni arrivavano con un periodo molto regolare di
circa 1.3 s. L’estrema regolarità del periodo e il fatto
che non si conoscesse alcun oggetto astronomico che
pulsasse così rapidamente fece subito pensare ad un
segnale emesso da una civiltà aliena intelligente.
L’ipotesi fu però scartata alcuni mesi dopo, dato che nel
cielo si trovarono numerose altre radiosorgenti di
12
questo tipo che vennero chiamate pulsar. Cosa
potevano essere queste pulsar? Gli astronomi iniziarono
col dire cosa non potevano essere. Si iniziò col dire che
non potevano essere stelle o nebulose ordinarie perché
anche se questi oggetti emettono onde radio le loro
emissioni non sono pulsanti. Esistono due principali
oggetti che possono emettere radiazioni pulsanti:
sistemi binari di stelle che si eclissano a vicenda (due
stelle che ruotano intorno ad uno stesso punto detto
centro di massa) e stelle variabili (stelle che variano
periodicamente la loro luminosità). I sistemi binari sono
però esclusi dalla terza legge di Keplero scritta alla
Newton. Per tale legge le due stelle dovrebbero ruotare
a 1000 km di distanza, ma tale distanza è minore del
raggio di qualsiasi stella ordinaria. Anche l’idea delle
stelle variabili fu scartata, perché queste hanno periodi
di giorni o settimane e non di secondi (così come le ali
di un’aquila non possono vibrare alla stessa frequenza
di quelle di un colibrì, una stella non può pulsare come
il nostro cuore). Rimaneva ancora una possibilità: le
pulsar potevano essere nane bianche rapidamente
rotanti aventi in un determinato punto della loro
superficie una sorgente di onde radio. Anche qui però
un problema: una nana bianca che ruota con un periodo
di un secondo dovrebbe essere sul punto di disperdersi
per problemi legati alla forza di gravità e alla forza
centripeta. L’idea delle nane bianche velocemente
rotanti fu definitivamente accantonata quando si scoprì
la pulsar della nebulosa del Granchio. Essa (la più
veloce a quel tempo con un periodo di 0.033 s, circa 30
volte al secondo) si trovava nella stessa identica
posizioni in cui l’astronomi cinese Yang Wei-T’e
avevano osservato quasi 1000 anni prima (1054) una
supernova (osservabile anche di giorno). Ciò
dimostrava che le pulsar non erano nane bianche ma i
resti di una supernova (stella di neutroni). Inoltre, visto
che una nana bianca non può rotare così velocemente, si
dimostrava che i resti di una supernova devono essere
qualcosa di molto più piccolo e compatto di una nana
bianca (cosa che negli anni sessanta non era affatto
accettata).
Il problema della rapida
rotazione di una stella
legato alla gravità e alla
forza centripeta è una
parziale risposta alla
domanda sollevata da
Loredana: Possono
esistere stelle normali
rapidamente rotanti e
dotate di un campo
magnetico tali da essere
considerate pulsar? No!
13
Le Pulsar sono stelle di neutroni con un intenso campo
magnetico e rapidamente rotanti.
Restano ancora alcune domande sulle pulsar a cui
dare risposta. Perché le stelle di neutroni dovrebbero
emettere onde radio? Perché la loro emissione dovrebbe
essere pulsante? Le risposte a queste domande sono
tutte legate alle piccole dimensioni di una stella di
neutroni. Essendo così piccola essa ruota molto
velocemente. Tutte le stelle ruotano attorno a un asse,
ma lo fanno molto lentamente (il nostro sole impiega
circa un mese per effettuare un giro completo). Però
esattamente come una ballerina che porta la petto le
braccia aumenta la velocità di rotazione, le stelle che
diminuiscono le loro dimensioni giungono a ruotare
molto velocemente (principio di conservazione del
momento angolare).
Le piccole dimensioni delle stelle di neutroni
spiegano anche la elevata intensità del campo
magnetico. Ogni stella porta con se un campo
magnetico, ma esso risulta distribuito su tutta la sua
superficie. Quando una stella massiccia diventa di
neutroni la sua superficie diminuisce di un fattore 1010
(dieci miliardi di volte) e il campo magnetico aumenta
di un analogo fattore. [come sappiamo il campo
magnetico di una stella è legato ai suoi gas ciò significa
che in qualche modo intorno alla stella di neutroni resta
del gas]
Infine dobbiamo capire come possa un campo
magnetico anche molto intenso come quello delle stelle
di neutroni inviare impulsi radio nello spazio. L’idea
oggi accettata è la seguente. I campi magnetici di una
stella di neutroni sono così intensi che parte della loro
energia può essere utilizzata per creare dal nulla coppie
di particelle e antiparticelle, per esempio elettroni e
positroni (che sono elettroni carichi positivamente).
Tali particelle vengono spinte dal campo magnetico
stesso a girare intorno all’asse magnetico. così facendo
emettono onde radio proprio lungo l’asse magnetico. La
pulsar è così una sorta di faro cosmico che ‘spara luce’
da due punti (dal nord magnetico e dal sud) esattamente
come alcuni fari terrestri.
Ecco un’altra parziale
risposta alla domanda di
Loredana. Le stelle normali
non hanno un campo
magnetico forte per cui non
sono in grado di “farsi
sentire” come pulsar.
Attenzione: il nostro
modello di Pulsar non
corrisponde perfettamente
alla realtà. La nostra pulsar
è solo un campo
magnetico rotante, manca
tutta la parte di creazione
di particelle e antiparticelle,
che accelerate dal campo
magnetico emettono onde
radio.
14
Emissioni
Radio
+
N
S
Asse Magnetico
Asse di Rotazione
La conservazione del momento angolare.
Per gli oggetti che vanno avanti e indietro esiste
una grandezza fisica detta massa inerziale m il cui
valore indica quanto sarà difficile far cambiare velocità
al corpo. Un libro ha una massa inerziale di 2 kg,
un’automobile di 1000 kg, allora sarà facile accelerare
o frenare un libro, difficile accelerare o frenare
un’automobile (provare per credere). Per gli oggetti che
ruotano intorno ad un punto esiste una grandezza
analoga detta momento di Inerzia I. Essa ci indica
quanto sarà difficile cambiare la velocità di rotazione
dell’oggetto: alto I significa che darà molto difficile,
basso I che sarà facile. Il valore di I dipende da come
sono distribuite le masse dell’oggetto rispetto al centro
di rotazione. Ad esempio se io decidessi di ruotare
intorno all’asse verticale testa piedi tenendo le braccia
aperte avrei masse distribuite lontano dall’asse e il mio
I sarebbe maggiore rispetto al caso in cui tenessi le
braccia conserte (cioè vicine all’asse di rotazione). La
distanza delle masse di un corpo dall’asse di rotazine si
indica solitamente con la lettera R. Per una sfera di
uniforme densità il momento di inerzia I vale:
15
2
MR 2
5
Dove M è la massa della stella ed R il suo raggio.
Esiste un principio della meccanica, il principio di
conservazione del momento angolare, che afferma che
il prodotto del momento di inerzia I di un corpo e della
sua velocità angolare si mantiene costante se non ci
sono forze esterne volte a influenzare la rotazione del
corpo. Ciò significa che quando una stella collassa visto
che I diminuisce con il quadrato del raggio R la w deve
aumentare per far sì che il prodotto I resti costante.
Possiamo fare un breve calcolo per renderci conto
dell’effetto nel caso del collasso di una stella.
Supponiamo che una stella collassi da dimensioni solari
( R 7 105 km) alle dimensioni di una stella di
I
neutroni ( R 16 km) senza perdite di massa. Allora il
principio di conservazione del momento angolare ci
dice che il momento angolare prima del collasso deve
essere uguale a quello dopo il collasso, cioè:
2
2
MR2 MR2 ,
5
5
R2 R2 ,
7 10
5 2
16 ,
2
2
7 10 5
2 10 9 .
16
Il che significa che la velocità di rotazione di una
stella di neutroni derivante da un sole aumenterebbe di
circa 2 miliardi di volte. Ovviamente non abbiamo
tenuto in considerazione che durante il collasso un
considerevole ammontare di materia abbandona la
stella…
Lorenzo Galante.
Liceo Scientifico Statale “Giordano Bruno” Torino.
Settembre 2006
16












