26/08/2010
Capitolo 4:
Modelli dinamici di sensori e
strumenti
Consideriamo il caso di uno strumento o di un sensore impiegato
per effettuare la misura di una grandezza meccanica variabile nel tempo.
Si hanno in ingresso e uscita dello strumento
delle funzioni del tempo e l’uscita è spesso un segnale di tipo elettrico.
Il legame dinamico tra due segnali, nel nostro caso l’ingresso e
l’uscita di uno strumento, si ottiene applicando le leggi fisiche che
ne governano la dinamica ed ottenendo un’equazioni differenziale
lineare a coefficienti costanti.
1
26/08/2010
Modello dinamico degli strumenti di misura
an
d nq0
d n −1q 0
d n qi
d n −1qi
+
a
+
...
+
a
+
b
+ ... + b1qi
n −1
1q 0 = bn
n −1
dt n
dt n −1
dt n
dt n −1
Dn =
Operatore differenziale
dn
dt n
anD n + an − 1D n −1 + ... + a1D + a 0 q 0 ( t ) = bnD n + bn − 1D n −1 + ... + b1D + b 0 qi ( t )
Si può definire quindi la FUNZIONE DI TRASFERIMENTO
q0
( D) =
qi
bnD n + bn − 1D n −1 + ... + b 0
anD n + an − 1D n−1 + ... + a 0
Esempio:
composizione delle funzioni di trasferimento operazionali in una
catena di misura
bn (iω )n + bn − 1 (iω )n −1 + ... + b0
q0
AD 2 + B K
q0
D=i
D=iω
ω
⋅
iω ) =
( D) =
(
qi
C
τ D +1
qi
an ( iω )n + an − 1 ( iω )n −1 + ... + a 0
Questa funzione esprime il rapporto tra due polinomi in campo complesso e quindi è
una funzione complessa di variabile reale w. Questa può essere espressa in forma
cartesiana con le sue due componenti parte reale Re(ω) e parte immaginaria Im(ω) o
in forma polare tramite la funzione modulo M(ω) e la funzione fase f(ω).
2
26/08/2010
RICHIAMI SULLE EQUAZIONI DIFFERENZIALI LINEARI A COEFFICIENTI COSTANTI
Una equazione differenziale lineare a coefficienti costanti ha la forma:
La sua soluzione è composta di due parti:
q0 = q0 g + q0 p
avendo indicato con:
-) q0 g l’integrale generale soluzione dell’equazione omogenea associata
-) q0 p l’integrale particolare dell’equazione che dipende dalla forma della funzione
àq0 g ha n costanti arbitrarie che dipendono dalle condizioni iniziali, cioè dai valori di q0, , all’istante t = 0.
àq0 p non ha nessuna costante arbitraria.
Per determinare q0 g esiste un metodo generale che consiste nel risolvere l’equazione algebrica associata
rispetto alla variabile D che, in generale è un numero complesso. L’equazione da risolvere è la:
Dn Dn-1
-Per ogni radice reale singola “s” si somma nella soluzione q0 g un termine del tipo C est;
-Per ogni radice reale “s” n-upla si somma nella soluzione q0 g un termine del tipo (C0+C1t+C2t 2+…+C n-1t n-1)
est;
-Per ogni radice complessa “a + ib” singola si somma nella soluzione q0 g un termine del tipo
C1 eat;
-Per ogni radice complessa “a + ib” n-upla si somma nella soluzione q0 g un termine del tipo
(C0+C1t+C2t2+…+Cn-1t n-1) eat.
La funzione di trasferimento di Laplace
È utile per studiare le caratteristiche dinamiche degli strumenti di misura e per risolvere più
semplicemente le equazioni differenziali con cui le si descrivono. I principali software
commerciali(Simulink di Matlab) di simulazione dinamica si basano su tale principio.
TRASFORMATA DI' LAPLACE
LINEARITA’ DELLA
TRASFORMATA DI LAPLACE
La funzione di trasferimento di
Laplace di uno strumento di misura è
definita come il rapporto della
trasformata di Laplace dell’ uscita
con la trasformata di Laplace dell’
ingresso, date le condizioni iniziali a
zero.
3
26/08/2010
Esempi di trasformata:
Strumenti di ordine zero
an
d nq0
d n −1q 0
d n qi
d n −1qi
+
a
+
...
+
a
+
b
+ ... + b1qi
n −1
n −1
1q 0 = bn
dt n
dt n −1
dt n
dt n −1
consideriamo nulli tutti i coefficienti tranne a0 e b0
a0 q0 ( t ) = b0 qi ( t )
Dividendo entrambi per a0
q0 ( t ) =
b0
qi ( t ) = kqi ( t )
a0
k è l’un unico parametro che definisce il modello di ordine zero
zero..
k rappresenta la sensibilità statica che risulta pari al rapporto tra uscita ed
ingresso, e quindi tra variazioni dell’uscita e dell’ingresso
dell’ingresso..
4
26/08/2010
Esempio: il Potenziometro
q0 e0
= =k
qi xi
FUNZ. DI
TRASFERIMENTO
k=
Eb
L
Il potenziometro è un sensore
che consente di misurare uno
spostamento rendendolo
proprio di un contatto a
scorrimento su di una
resistenza elettrica.
Variando la posizione del
contatto mobile si varia la
tensione di uscita e0 se la
resistenza totale del
potenziometro è alimentata con
una tensione E
M = a 2 + b2 = k 2 = k
M = k
q0
(iω ) = k →
Im 0
∀ω
qi
tan
φ
=
=
=
0
→
φ
=
0
Re k
Funzione di trasferimento sinusoidale dello strumento di ordine zero
Il segnale in uscita ha la stessa forma di quello di ingresso con ampiezza
scalata del fattore K e senza ritardo di fase. Pertanto è uno strumento
ideale per misure dinamiche.
Un altro esempio di dispositivo che può considerarsi di ordine zero è l’amplificatore
operazionale. Questi vengono largamente impiegati in catene di misura per amplificare
segnali in modo da renderli meno sensibili a disturbi di tipo elettromagnetico. Inoltre i
segnali sono più facilmente rilevabili ed è possibile eseguire la somma, la
differenza,comparare due segnali in tensione infine effettuare la derivata o l’integrale.
5
26/08/2010
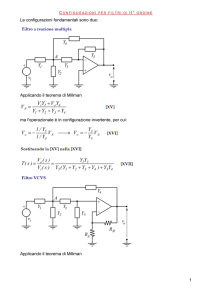
Illustrazione e schema elettrico di un amplificatore operazionale
L’amplificatore operazionale può essere utilizzato per amplificare o attenuare un
segnale in due configurazioni tipiche:
invertente
non invertente.
controreazione realizzata tramite le
resistenze RS ed RF
Per la legge di Ohm e Kirchoof
se il guadagno Aol ha un valore
elevato
6
26/08/2010
In realtà il guadagno di un amplificatore operazionale reale non è infinito e la sua
risposta non è costante per ogni frequenza. Si può esprimere il guadagno in deciBel
(dB
dB)) come Av(dB
dB)) =20 log10 (eo/ei) e definiamo ampiezza di banda BW l’intervallo di
frequenze da zero al punto in cui la funzione di risposta in frequenza diminuisce di 3
dB.. Il dispositivo può essere caratterizzato dal prodotto (A
dB
(Av BW).
Esempi di applicazioni
7
26/08/2010
Strumenti di ordine 1
a1
τ
dq0
+ a0 q0 = b0 qi
dt
dq0
+ q0 = kqi
dt
q0
k
(D) =
τ D +1
qi
Divido per ao
b
a1 dq0
+ q0 = 0 qi
a0 dt
a0
Inser
Insereendo
l’operatore D
τ Dq0 + q0 = kqi
Sostituendo
iw a D
q0
k
( iω ) =
qi
τ iω + 1
Un esempio classico di strumento di ordine uno è un generico sensore di temperatura o
un semplice termometro a mercurio. Supponendo, che in quest’ultimo, lo scambio di
calore,tra bulbo e mercurio,avviene esclusivamente per convezione si può scrivere il
seguente bilancio energetico.
hA ⋅ Tf = V ⋅ ρ ⋅ c p ⋅
dT b
+ hA ⋅ Tb
dt
V ⋅ ρ ⋅ c p dq0
⋅
+ q0 = qi
hA
dt
k = 1
V ⋅ ρ ⋅ cp
τ =
hA
8
26/08/2010
Per determinare le prestazioni dinamiche degli strumenti di misura si utilizzano
tipicamente ingressi campione standard. Se abbiamo uno strumento di ordine
uno che viene sottoposto ad un ingresso a gradino si ha:
τ Dq0 + q0 = kqi → (τ D + 1) q0 = kqis
−t
q0 = 1 − e τ
⋅ kqis
−t
soluzione Eq
Eq.. Differenziale
q0 = c ⋅ e τ + kqis
con le condizione iniziale q0 = 0 per t = 0
Esempi di strumenti di ordine 1
9
26/08/2010
Risposte di uno strumento di ordine 1 a diversi segnali di ingresso
RISPOSTA IN FREQUENZA
Per determinare la risposta ad ingressi sinusoidali (risposta in frequenza) degli
strumenti di ordine uno si applica il metodo delle trasformate di Laplace.
Risposta in frequenza di uno strumento del primo ordine
10
26/08/2010
Strumenti di ordine due
ESEMPIO..
V = iR +
q
di
+L
C
dt
L
d 2q
dq 1
+R
+ q =V
dt 2
dt C
equazione differenziale del secondo ordine
1 d 2 qo 2ξ dqo
⋅
+
⋅
+ qo = Kqi
ωn2 dt2 ωn dt
11
26/08/2010
.
1 d 2 qo 2ξ dqo
⋅
+
⋅
+ qo = Kqi
ωn2 dt 2 ωn dt
Funzione di trasferimento di Laplace degli
strumenti del secondo ordine
Moltiplicata per 1/s
f O (s ) =
qo (s )
= KG(s )
qi (s )
trasformata di Laplace
G(s ) =
1
2ξ
s2 + s + 1
2
1
ωn
f O (s ) =
ωn
1
1 2 2ξ
2s +
s + 1 s
ω
ωn
n
1
1
ξω n
(s + 2ξωn )
(s + ξω n )
(s + 2ξω n )
1
−
= −
−
−
=
s (s + ξωn )2 + ω n 2 (1 − ξ 2 ) s (s + ξω n )2 + ωn 2 (1 − ξ 2 ) (s + ξωn )2 + ωn 2 (1 − ξ 2 )
s s 2 + 2ξω n s + ω n 2
Ci sono tre casi da considerare dipendenti a seconda che
ξ > 1, ξ = 1, ξ < 1
risposta di uno
strumento del
secondo ordine ad un
gradino unitario
12
26/08/2010
risposta dello
strumento di
ordine due alla
rampa
Risposta
all’impulso
dello
strumento
del secondo
ordine
G (s ) =
1
ωn2
1
2ξ
⋅ ( jω ) +
2
ωn
⋅ ( jω ) + 1
Risposta in
frequenza di uno
strumento del
secondo ordine
Esprimendo questa
funzione come
modulo e fase
valore massimo
G ( jω ) =
G( jω ) MAX =
1
ω 2 2
ω2
1 − 2 + 4ξ 2 2
ωn
ωn
1
2ξ 1 − ξ
2
2ξ ω ω
n
arg G ( jω ) = − tan −1
2
2
1 − ω ω n
ωR = ωn 1 − 2ξ 2
frequenza
di risonanza
13
26/08/2010
Elementi a tempo morto
Ne sono un esempio le linee di trasmissione elettriche, pneumatiche, ottiche, o la
trasmissione del suono in aria.
q 0 = kq i (t − τ )
Quindi ad un ingresso a gradino corrisponde un uscita a gradino ritardata di τ
e amplificata di k, se ho un ingresso a rampa otterrò un uscita a rampa ritardata.
qi = Ai sen (ωt )
q0 = KAi sen(ω(t − τ ))
qo
(iω ) = K∠ − ωτ
qi
Filtri
E’ utilizzato per eliminare da un ingresso i disturbi in esso presenti. Può essere applicato
anche all’uscita. I filtri possono essere di vario tipo, i più comuni sono:
• meccanici;
• idraulici;
• termici;
• elettrici.
Si possono dividere in attivi o passivi:
• gli attivi utilizzano una fonte di energia esterna per funzionare;
• i passivi utilizzano una parte dell’energia del segnale per filtrare lo stesso.
Classificazione secondo la funzione di trasferimento
14
26/08/2010
Filtro passopasso-basso
Permettono il passaggio delle armoniche la cui frequenza è inferiore ad una frequenza
specifica detta frequenza di taglio
1
Filtro
Reale
Filtro
Funzione di
trasferimento di un
filtro passa basso
Ideale
Frequenza
Filtro meccanico
Filtro idraulico
Filtro termico
Schema elettrico di un filtro passivo passo
passo--basso
Schema elettrico di un filtro attivo passo
passo--basso
15
26/08/2010
Filtro passo alto
Tali filtri permettono che solo frequenze superiori alla frequenza di taglio possano passare,
eliminando le altre.
Confronto tra un filtro
passa alto reale e uno
ideale
Filtro meccanico
Filtro idraulico
Schema elettrico di un filtro passivo passo
passo--alto
Schema elettrico di un filtro attivo passopasso-alto
16
26/08/2010
.
Filtri passa banda
La composizione di un filtro passa basso e di uno passa banda costruisce un filtro passa banda la cui
frequenza è compresa tra
e
Schema elettrico di un filtro passivo passa banda
Schema elettrico di un filtro passivo passa banda
Filtro taglia bando
Tali filtri permettono il passaggio delle armoniche fuori dalla banda compresa tra due
frequenze una inferiore
e una superiore
17
26/08/2010
Determinazione sperimentale dei parametri dei modelli dinamici
degli strumenti
E’ possibile determinare le caratteristiche dinamiche di uno
strumento se è noto il tipo di modello che lo impiegando un
ingresso dinamico campione.
Per strumenti del primo ordine come parametro dinamico si
usa la costante di tempo. Per determinare quest’ultima si può
eseguire un test al gradino.
−
q 0 − kqis
=e τ
kqis
t
La risposta è di tipo
esponenziale
Si può operare interpolando tutta la
risposta. Si determina,con il metodo dei
minimi quadrati , la pendenza della retta
rappresentata dalla seguente funzione:
Z = ln
q 0 − kq is
= −t / τ
kq is
Anche per strumenti del secondo ordine si possono determinare i due parametri
che li caratterizzano, frequenza naturale e rapporto di smorzamento, con un test al
gradino. La risposta per strumenti sotto smorzati è del seguente tipo:
18
26/08/2010
ESEMPI
1) Risposta al gradino con SMULINK di strumenti del primo ordine
Consideriamo un sensore di temperatura con sensibilità
statica K=46 mV/K e costante di tempo τ=10 s.
46
46
10s+1
10s+1
Step
T ransfer Fcn
Scope
Transfer Fcn
500
q0 [mV]
400
300
X: 11
Y : 290.8
X: 9
Y : 253.3
200
100
0
0
10
20
30
40
50
60
70
80
90
100
Tempo [s]
2) Risposta alla rampa con SMULINK di strumenti del primo ordine
46
46
10s+1
Ramp
10s+1
Ramp
Scope
Transfer Fcn
Scope
T ransfer Fcn
46
simou t
Gain
T o Workspace
5000
4500
4000
q0 [mV]
3500
3000
2500
2000
1500
1000
500
0
0
10
20
30
40
50
60
70
80
90
100
Tempo [s]
3) Risposta dello strumento di ordine uno all’impulso
1
4.5
0.9
4
0.8
Scope
simou t
kqi/τ [mV]
10s+1
Tran sfer Fcn
q0 [mV]
46
Discrete
Impulse
3.5
0.7
0.6
0.5
0.4
2
1.5
0.3
1
0.2
0.5
To Workspa ce
0.1
0
0
3
2.5
0
0
10
20
30
40
50
60
70
80
90
100
Tempo [s]
10
20
30
40
50
60
70
80
90
100
Tempo [s]
19
26/08/2010
4) Risposte degli strumenti del secondo ordine al gradino
180
ξ=0.1
160
140
100
0.0001s2 +0.02s+1
Tran sfer Fcn
120
qo [mV]
Step
Scope
simout
100
ξ=1
80
ξ=2
60
To Workspace
40
20
0
0.5
1
1.5
2
2.5
3
Tempo [s]
5) Risposta degli strumenti del secondo ordine alla rampa
5
4.5
4
Gain
Scope
100
0.0001s2 +0.02s+1
Ramp
Transfer Fcn
qo e qi [mV]
100
3.5
3
2.5
2
1.5
simout
To Workspace
1
0.5
0
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
0.045
0.05
Tempo [s]
20