EFFETTO FOTOELETTRICO
PREMESSA
Planck non riusciva a credere che un oscillatore potesse esistere solo in livelli discreti
di energia, perché l’idea di continuità metteva in crisi la stessa concezione del campo
elettromagnetico continuo: se l’energia si conserva durante il processo di emissione,
una quantità fissa di energia hv deve improvvisamente essere trasferita al campo e
questo comporta una qualche localizzazione nello spazio (Vedi pag.22 del Corpo
Nero) che si accorda male con l’idea di un campo continuo presente ovunque.
Perciò Planck considerava la sua stessa ipotesi della quantizzazione un argomento
euristico cioè, basata su un’idea utile, ma probabilmente non vera che permetteva di
conseguire un risultato da verificare poi in modo rigoroso.
E in questo sbagliava( Esperimento di Franck e Hertz).
La scoperta e il tentativo di spiegazione dell’effetto fotoelettrico aprì un altro
momento di grave crisi per la teoria classica della radiazione elettromagnetica!
I.
EFFETTO FOTOELETTRICO
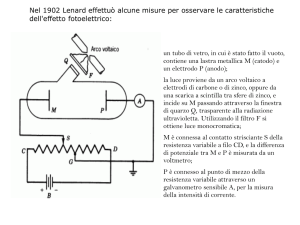
L'effetto fotoelettrico fu scoperto da Hertz e Hallwachs nel 1887. L'effetto consiste
nell'emissione di elettroni da parte di superfici metalliche irraggiate con radiazione
elettromagnetica.
Detta v la frequenza della radiazione ed I la sua intensità, le principali
caratteristiche osservative di tale fenomeno sono:
frequenza di soglia
dipende dal materiale
1. Si verifica solo se v v0
2. L'energia cinetica massima degli elettroni, Ecin,MAX , che fuoriescono dal materiale è
indipendente dall'intensità, I , della radiazione incidente.
3. Il numero, ne , degli elettroni emessi per unità di tempo è direttamente
proporzionale a I .
4. L'energia cinetica massima degli elettroni, Ecin,MAX , dipende in modo lineare dalla
frequenza v mediante la relazione: Ecin,MAX a We , con We una costante che
dipende dal materiale colpito dalla radiazione, sperimentalmente risulta: a h .
5. Gli elettroni sono emessi istantaneamente.
1
L'amperometro A consente di misurare l'intensità di corrente massima nel circuito,
cioè il numero, ne , degli elettroni emessi per unità di tempo dal metallo.
Lo stesso apparato consente di misurare anche l'energia cinetica massima, Ecin,MAX ,
con cui ciascuno di essi è emesso. Cambiando, infatti, segno alla d.d.p. V , essa si
oppone al moto degli elettroni emessi dal metallo: nessuno degli elettroni emessi
potrà raggiungere gli altri elementi del circuito se eVArresto Ecin,MAX .
L'elettromagnetismo classico, anche in questo caso, si rivela inadeguato nella
predizione corretta dei risultati sperimentali, 1), 2), 4),5).
Infatti, per la teoria di Maxwell, la luce non è altro che un’onda continua, fornita di
proprietà omogeneamente distribuite nel volume che occupa. In particolare essa
trasporta energia e quantità di moto distribuiti secondo la descrizione fornita dal
vettore di Poynting, e quindi omogeneamente in tutto lo spazio. Aumentare l’intensità
dell’onda significa aumentare il modulo dei vettori campo elettrico e campo
magnetico, il che implica un aumento della densità energetica presente in ogni punto
dell’onda. Pertanto quella parte dell’onda che investe un certo elettrone alla
superficie del catodo gli dovrebbe cedere, a parità di tempo di esposizione, tanta più
energia quanto maggiore è la sua intensità. Non si riesce a capire come l’energia
cinetica del fotoelettrone possa essere indipendente dall’intensità della luce.
1
2
Trattando, infatti, il fascio di luce come un'onda piana con intensità I c 0 E02
esercita sull'elettrone, per mezzo del campo elettrico associato E0 , una forza
F eE0 I e di conseguenza l'energia cinetica, ECin , acquistata dall'elettrone
risulta ECin I secondo un coefficiente che non dipende dalla frequenza v della
radiazione incidente. Non è quindi possibile spiegare come possa esistere una
frequenza di soglia v0 . Inoltre, l'energia cinetica aumenta con I e non con la
frequenza in contrasto con i dati sperimentali. Considerando poi il raggio re
dell'elettrone, secondo la descrizione classica, nel tempo t viene conferita dalla
radiazione un'energia pari a: ECin I t re2 . Per il potassio che richiede un lavoro di
estrazione We 3.44 1019 J si ottiene, per un tempo t 107 s e un'intensità
I 101W / m2 , un raggio dell'elettrone re 3.3 m !! Ovviamente assurdo!
Dopo il 1902 cominciò a farsi strada che qualcosa di fondamentale dovesse essere
cambiato nella descrizione della luce.
Einstein nel 1905 risolse il problema assumendo che:
“ La luce pur mantenendo le sue caratteristiche ondulatorie, avesse una
distribuzione non uniforme dell’energia, essendo costituita da certe piccolissime
regioni (QUANTI, o CORPUSCOLI della radiazione). La radiazione
monocromatica di bassa densità si comporta in senso termodinamico, come se
consistesse di QUANTI DI RADIAZIONE mutuamente indipendenti di
grandezza h “ .
O ancora:
2
“ Secondo l’ipotesi che voglio qui proporre, quando un raggio di luce si espande
partendo da un punto, l’energia non si distribuisce su volumi sempre più grandi,
bensì rimane costituita da un numero finito di quanti di energia localizzati nello
spazio e che si muovono senza suddividersi, e che non possono essere assorbiti o
emessi parzialmente”.
Einstein non pensava alla descrizione puramente corpuscolare della luce, le equazioni
di Maxwell non potevano essere cancellate con un colpo di spugna. Einstein, tuttavia
credeva, nell’esistenza di un’onda che accompagnasse il corpuscolo energetico nella
sua propagazione e che ne determinasse il comportamento. Questa era un’onda
vuota di energia e quantità di moto, con caratteristiche completamente nuove
rispetto a tutte le onde studiate dalla fisica classica. D’altra parte, i fenomeni
d’interferenza e diffrazione non possono essere certo spiegati da una concezione
puramente corpuscolare.
Questo consentì ad Einstein di spiegare immediatamente l'effetto fotoelettrico:
- un fotone cede per urto la sua energia h a un elettrone di conduzione del metallo,
questo è emesso istantaneamente con energia cinetica ECinMax in ottemperanza alla
conservazione dell'energia: h ECinMax We , con We h 0 lavoro di estrazione -.
Tale formula fu verificata rigorosamente da Millikan una decina di anni più tardi
(1916) che definirà l'ipotesi dei quanti di luce come << audace, per non dire
incauta innanzitutto perché una perturbazione elettromagnetica che rimane
localizzata nello spazio appare come una violazione del concetto stesso di
perturbazione elettromagnetica, e secondariamente perché contrasta
apertamente con i ben stabiliti fatti dell'interferenza. >>
Questa nuova descrizione della luce (corpuscoli energetici, più onde vuote di energia)
secondo Einstein non era in conflitto con tutte le osservazioni sperimentali che fino
ad allora avevano indicato una natura ondulatoria della luce, perché (sempre parole di
Einstein, 1905 ): << Bisogna tenere presente che le osservazioni ottiche si
riferiscono a valori medi nel tempo e non a valori istantanei; sebbene abbiano
trovato assoluta conferma la teoria della diffrazione, della riflessione, della
rifrazione, della dispersione, ecc… , è pensabile che la teoria della luce fondata
su funzioni spaziali continue possa entrare in conflitto con l’esperienza, qualora
venga applicata ai fenomeni di emissione e trasformazione della luce.>>
Einstein (1909) dimostrò che la formula di Planck si accordava bene con la sua
concezione del campo elettromagnetico studiando le fluttuazioni energetiche della
radiazione elettromagnetica di una cavità( dovute ad esempio alle fluttuazioni di
temperatura, ecc.). Infatti, nella formula di Planck contribuiscono additivamente gli
aspetti ondulatori e gli aspetti corpuscolari della radiazione elettromagnetica, come
può notarsi calcolando lo scarto quadratico medio dell’energia dal suo valor medio:
E
2
E
E
2
c3 E 2
Ehv
8 v3dv V
Infatti, Il primo termine è ciò che si otterrebbe se per v, T fosse valida
l’approssimazione di Rayleigh ( v, T
3
8 k 2
v T ), per
c3
hv valida nella
concezione ondulatoria; il secondo termine è ciò che si otterrebbe se per v, T
fosse valida l’approssimazione di Wien ( v, T
8 h 3 hv kT
ve
)per
c3
hv valida
nella concezione corpuscolare.
Questa conclusione può sembrare sorprendente se si pensa che secondo Einstein
l’energia della radiazione è tutta concentrata in corpuscoli. Diventa comprensibile
però se si considera che l’onda elettromagnetica influisce sul comportamento
delle particelle (gli oscillatori), costringendole a ridistribuirsi energeticamente a
seconda delle sue variazioni. La formula di Planck può essere riscritta come
8 h
nhv
E En con En 3 v3 exp
dvV mostrando che descrive la somma di tanti
kT
n 1
c
diversi “ gas ” di quanti elettromagnetici, il primo con energia hv , il secondo con
energia 2hv , …l’n – esimo con energia nhv , ecc. Questo risultato può essere così
interpretato: l’entità fondamentale della radiazione di corpo nero è il pacchetto
d’onde, cioè l’entità estesa emessa nelle singole transizioni atomiche , ed, il
pacchetto può contenere, a seconda dei casi , un quanto energetico, o due quanti,
o tre, ecc. I pacchetti si comportano indipendentemente l’uno dall’altro e
indipendentemente dal numero di quanti energetici in essi contenuto. La
presenza di più di un quanto di energia in un determinato pacchetto d’onde è dovuta
all’azione dell’onda su un atomo eccitato e alla conseguente estrazione da
quell’atomo di un quanto di energia, che da quel momento in poi si andrà ad
aggiungere agli altri quanti di energia presenti nell’onda stimolatrice inserendosi così
a pieno titolo in essa (emissione stimolata). Inoltre per la scarto quadratico medio
2
delle fluttuazioni di energia si scrive E hvE1 2hvE2 3hvE3 .... . Questo risultato
ha la seguente interpretazione: Lo scarto quadratico medio è la somma di
fluttuazioni corpuscolari di entità hv , più fluttuazioni 2hv , ecc. Paragonandolo al
risultato precedente, si osserva che il termine corpuscolare è rimasto inalterato
(vi è solo la sostituzione di E con E1 ), mentre il termine ondulatorio
c3 E 2
si è
8 v3dv V
scisso in un’infinità di contributi dovuti alle correlazioni fra due quanti
d’energia, fra tre quanti energetici, ecc. E’ l’onda elettromagnetica che
introduce correlazioni aggiuntive fra i corpuscoli.
4