CompitoParziale2_CiviliInformatici_2011.nb
1
COMPITO PARZIALE CIVILI INFORMATICI - 21/01/2011
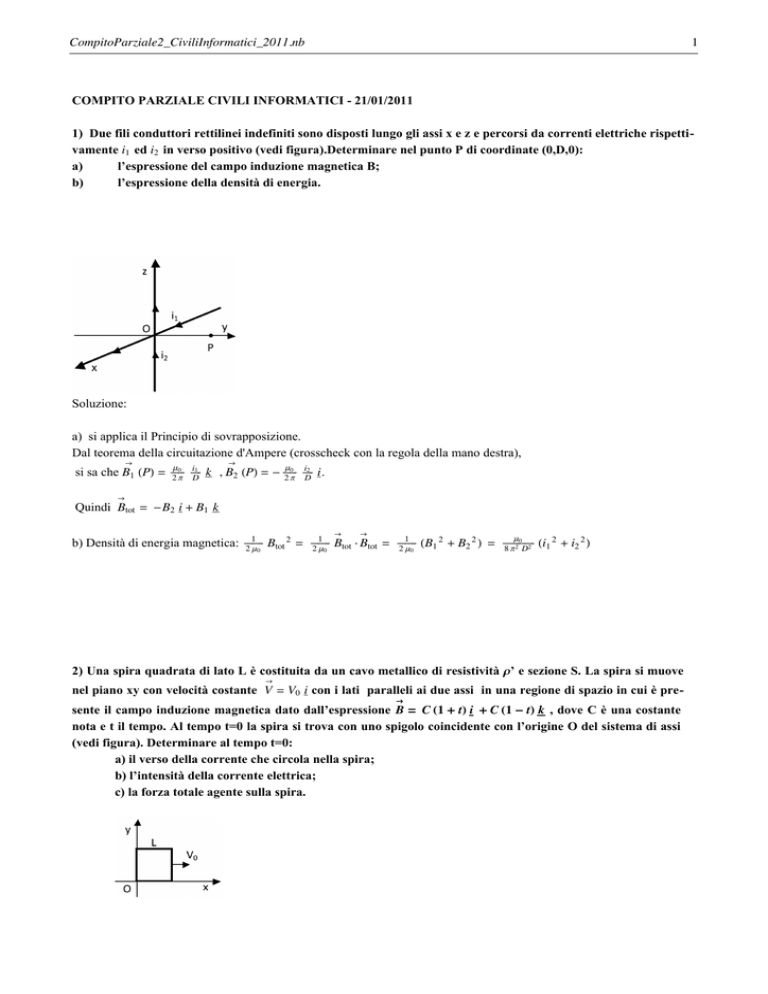
1) Due fili conduttori rettilinei indefiniti sono disposti lungo gli assi x e z e percorsi da correnti elettriche rispettivamente i1 ed i2 in verso positivo (vedi figura).Determinare nel punto P di coordinate (0,D,0):
a)
l’espressione del campo induzione magnetica B;
b)
l’espressione della densità di energia.
Soluzione:
a) si applica il Principio di sovrapposizione.
Dal teorema della circuitazione d'Ampere (crosscheck con la regola della mano destra),
m0 i1
m0 i2
si sa che B1 HPL = ÅÅÅÅ
ÅÅÅÅ ÅÅÅÅÅ k , B2 HPL = - ÅÅÅÅ
ÅÅÅÅ ÅÅÅÅÅ i.
2 p D êê
2p D ê
Ø
Ø
Ø
Quindi Btot = -B2 êi + B1 êkê
m0
b) Densità di energia magnetica: ÅÅÅÅ
Å1ÅÅÅÅÅ Btot 2 = ÅÅÅÅ
Å1ÅÅÅÅÅ Btot ÿ Btot = ÅÅÅÅ
Å1ÅÅÅÅÅ HB1 2 + B2 2 L = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅ Hi1 2 + i2 2 L
2 m0
2 m0
2 m0
8 p2 D2
Ø
Ø
2) Una spira quadrata di lato L è costituita da un cavo metallico di resistività r’ e sezione S. La spira si muove
Ø
nel piano xy con velocità costante V = V0 êi con i lati paralleli ai due assi in una regione di spazio in cui è presente il campo induzione magnetica dato dall’espressione B = C H1 + tL èi + C H1 - tL èè
k , dove C è una costante
nota e t il tempo. Al tempo t=0 la spira si trova con uno spigolo coincidente con l’origine O del sistema di assi
(vedi figura). Determinare al tempo t=0:
a) il verso della corrente che circola nella spira;
b) l’intensità della corrente elettrica;
c) la forza totale agente sulla spira.
Æ
Soluzione:
Ø
a) Il flusso del campo magnetico B attraverso la spira si scrive in generale come
F(t) = ‡ B ÿ „ S, dove scegliamo la convenzione di assumere dS = dS êkê.
Ø
Ø
Ø
CompitoParziale2_CiviliInformatici_2011.nb
2
Soluzione:
Ø
a) Il flusso del campo magnetico B attraverso la spira si scrive in generale come
F(t) = ‡ B ÿ „ S, dove scegliamo la convenzione di assumere dS = dS êkê.
Ø
Ø
Ø
S
Quindi
F(t) = ŸS H C H1 + tL êi + C H1 - tL êkêL ÿ dS êkê = ŸS C H1 - tL dS = C H1 - tL ŸS dS = C S H1 - tL .
Ø
In sostanza: il campo magnetico è variabile nel tempo, ma è omogeneo spazialmente e quindi il flusso di B attraverso la
superficie della spira non dipende dalla posizione della stessa.
Per il flusso conta soltanto il campo magnetico nella sua componente lungo z.
Ora, quello che succede quindi è che con il passare del tempo, fintanto che t < 1 il flusso diminuisce ma resta F (t) >0.
Per t =1, il F(0)=0 ; poi per t>1, F(t)<0.
In sostanza il flusso diminuisce sempre.
Ora, per la legge di Faraday Neumann e Lens, che asserisce che la corrente indotta deve instaurarsi in modo da compensare la variazione di flusso, si può dire che la corrente circola sempre in senso antiorario.
d
Infatti, la f.e.m. indotta è costante: eind = - ÅÅÅÅ
ÅÅ FHtL = C S.
dt
r
b) Essendo sia la resistività che la sezione della spira delle costanti, Rspira = 4 ÅÅÅÅ
ÅÅÅÅ!ÅÅ . Di conseguenza, per la legge di
è!!!
S
Ohm,
è!!!!
CS S
C L3
il modulo della corrente indotta Iind = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅ = ÅÅÅÅÅÅÅÅ
ÅÅÅÅ .
4r
4r
c) Per la legge di Biot-Savart, la forza che si applica sulla spira vale Fmag = ‡
Ø
Ø
I dl ä B . Siccome il campo è omoge-
circ
neo, le forze indotte sui lati opposti si compensano e la risultante delle forze è nulla.
3) Forza su spira rettangolare rigida di base a=20 cm ed altezza b=10cm è percorsa in senso antiorario da una
corrente elettrica costante i0 = 1A ed è ferma nel piano (xy) con il centro nell’origine degli assi (vedi figura).
Nello spazio è presente un campo il campo induzione magnetica B = B0 H1 + ÅÅÅÅby L êj . Determinare modulo, direzione e verso della forza totale agente sulla spira.
Ø
Soluzione
Fmag = ‡
Ø
circ
= ‡
I dl ä B = ‡
Ø
-I dl êi ä B + ‡
Ø
y= ÅÅb2ÅÅ
-I dl êi ä B + ‡
Ø
y= ÅÅb2ÅÅ
Ø
x=- ÅÅa2ÅÅ
I dl êi ä B + ‡
Ø
y=- ÅÅb2ÅÅ
Ø
x= ÅÅa2ÅÅ
I dl êj ä B =
I dl êi ä B = -I a B0 J1 + ÅÅÅÅb2ÅÅ N êkê + I a B0 J1 - ÅÅÅÅb2ÅÅ N êkê = -I a B0 êkê
Ø
y=- ÅÅb2ÅÅ
- I dl êj ä B + ‡
ÅÅbÅÅ
ÅÅbÅÅ
4) Il circuito mostrato in figura è composto da due induttanza L1 = L2 = 1 mH, quattro resistenze rispettivamente del valore R1 = R2 =60W ed R3 = R4 =80W, da tre condensatori di capacità C1 = C2 = C3 =10mF, da due
generatori di forza elettromotrice rispettivamente ¶ε1 = 60 V ed ¶ε1 = 90 V e resistenza interna trascurabile e da
= ‡
2
-I dl êi ä B + ‡
y= ÅÅb2ÅÅ
I dl êi ä B = -I a B0 J1 +
2
Ø
Ø
y=- ÅÅb2ÅÅ
ÅÅbÅÅ
ÅÅÅÅb2ÅÅ N
êkê + I a B0 J1 2
ÅÅbÅÅ
ÅÅÅÅb2ÅÅ N
2
êkê = -I a B0 êkê
CompitoParziale2_CiviliInformatici_2011.nb
3
4) Il circuito mostrato in figura è composto da due induttanza L1 = L2 = 1 mH, quattro resistenze rispettivamente del valore R1 = R2 =60W ed R3 = R4 =80W, da tre condensatori di capacità C1 = C2 = C3 =10mF, da due
generatori di forza elettromotrice rispettivamente ¶ε1 = 60 V ed ¶ε1 = 90 V e resistenza interna trascurabile e da
un interruttore T inizialmente aperto. Determinare
a) la corrente elettrica che circola nelle quattro resistenze in funzione del tempo;
Determinare in regime stazionario (t Æ •):
b) il valore del potenziale nel punto A;
c) l’energia totale immagazzinata nel sistema.
d) la potenza dissipata nel sistema.
Soluzione
In virtù della f.e.m. e2 , che mantiene la d.d.P costante tra i suoi capi, il circuito si splitta in due circuiti indipendenti.
Circuito A: si identifica con la maglia di sinistra, e pertanto è un banale circuito RL, con
R3 R4
RA = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅ = 40 W,
R3 +R4
LA = L1 + L2 = 2 mH;
la f.e.m. vale eA = e2 , e solo per questo circuito ha senso fare il conto delle correnti nel tansitorio.
Circuito B: si identifica con la maglia di destra, ed è un circuito RC, ma in esso non circola corrente, a causa di C1 o
C3 , che tengono sempre aperto il circuito. La f.e.m. da considerare è eB = e1 + e2 = 150 V. Siccome non circola
corrente, per la legge di Ohm ai capi delle resistenze R1 e R2 non ci sono cadute ohmiche; questo implica in particolare
che il condensatore C2 è scarico, non avendo nessuna d.d.P. ai suoi capi.
Quindi in pratica si può schematizzare ulteriormente il circuito come un circuito con soli i condensatori C1 e C3
C1 C3
disposti in serie, cui corrisponde una capacità complessiva CB = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅ = 5 m F, che presenta una d.d.P. ai suoi capi
C1 +C3
pari a eB .
--Detto questo:
a) Il transitorio si ha soltanto nel circuito A, ed è immediato risolvere l'equazione differenziale lineare di primo grado
non omogenea
d
eA = RA IA + LA ÅÅÅÅ
ÅÅ I ,
dt A
che ha come soluzione
eA
IA HtL = ÅÅÅÅ
ÅÅÅÅ J1 - e
RA
R
A
- ÅÅÅÅ
LÅÅ Å Å t
A
N;
quindi
R4
in R3 circola IA HtL ÅÅÅÅ
ÅÅÅÅ ;
RA
R3
in R4 circola IA HtL ÅÅÅÅ
ÅÅÅÅ ;
RA
e come già detto, in R1 e R2 non circola mai corrente.
b) A regime stazionario, il potenziale nel punto A vale 0, dato che è direttamente collegato alla massa (le induttanze
d
non rappresentano nessuna caduta di tensione quando ÅÅÅÅ
ÅÅ I = 0).
dt
c) A regime stazionario, si immagazzina energia nell'induttanza LA e nella capacità CB , pari a
eA 2
Utot = ÅÅÅÅ12 LA IA H¶L2 + ÅÅÅÅ12 VB 2 CB = ÅÅÅÅ12 ALA I ÅÅÅÅ
ÅÅÅÅ M + eB 2 CB E = 0.51 10-2 + 5.62 10-2 J = 6.13 10-2 J.
RA
eA
d) A regime, si dissipa potenza solo in RA , con potenza W = IA H¶L2 RA = ÅÅÅÅ
ÅÅÅÅÅ = 202.5 W
RA
2
e come già detto, in R1 e R2 non circola mai corrente.
b) A regime stazionario, il potenziale nel punto A vale 0, dato che è direttamente collegato alla massa (le induttanze
d
CompitoParziale2_CiviliInformatici_2011.nb
4
non rappresentano nessuna caduta di tensione quando ÅÅÅÅ
ÅÅ I = 0).
dt
c) A regime stazionario, si immagazzina energia nell'induttanza LA e nella capacità CB , pari a
eA 2
Utot = ÅÅÅÅ12 LA IA H¶L2 + ÅÅÅÅ12 VB 2 CB = ÅÅÅÅ12 ALA I ÅÅÅÅ
ÅÅÅÅ M + eB 2 CB E = 0.51 10-2 + 5.62 10-2 J = 6.13 10-2 J.
RA
eA
d) A regime, si dissipa potenza solo in RA , con potenza W = IA H¶L2 RA = ÅÅÅÅ
ÅÅÅÅÅ = 202.5 W
RA
2
5) Discutere le seguenti affermazioni specificando se sono vere o false:
I.
il campo elettrico generato da un campo B variabile nel tempo ha divergenza nulla;
Ø
Ø
Ø
Ø
¶∂ B
[vero] , infatti la III eq. di Maxwell, “ ä E = - ÅÅÅÅ
ÅÅÅÅ , ci dice che E non è irrotazionale, quando generato da un B
¶∂ t
variabile nel tempo. Questo si vede bene scrivendo la forma integrale della stessa equazione: ‡
circuito
Ø
d
E ÿ „ l = - ÅÅÅÅ
ÅÅ FJBN.
dt
Ø
Ø
Ø
In questo caso appare ben evidente che l'integrale di E lungo un cammino chiuso è diverso da zero, se il flusso di B
varia nel tempo (ma per scrivere questa forma è stata ipotizzata l'indipendenza dal tempo delle coordinate spaziali,
Ø
ovvero la geometria del circuito non dipende dal tempo). La circolarità di E, detta più correttamente solenoidalità,
Ø
Ø
implica che “ ÿ E = 0.
II.
il tempo caratteristico di un circuito RL è pari a t=LR;
L
[falso] è ÄÄÄÄÄ
, come si può dalla verifica delle dimensioni:
R
@FHBLD
t
@ED
t
@VD 2 l
m l2 t-2 t2
m l2
@LD = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ = @BD l2 ÅÅÅÅ
ÅÅ = ÅÅÅÅ
ÅÅÅÅ t l2 ÅÅÅÅÅ
= ÅÅÅÅ
ÅÅÅÅÅ t ÅÅÅÅÅ
= ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅ ÅÅÅÅ
Å = ÅÅÅÅ
ÅÅÅÅÅÅ ;
@ID
Q
l
Q
l
Q
Q
Q
Q2
@VD
ml t
t
ml t
@RD = ÅÅÅÅ
ÅÅÅÅÅ = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅ ÅÅÅÅÅ
= ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅ
@ID
Q
Q
Q2
2 -2
2 -1
@LD
ml
quindi ÅÅÅÅ
ÅÅÅÅ = ÅÅÅÅ
ÅÅÅÅÅÅ ÅÅÅÅÅÅÅÅQÅÅÅÅÅÅÅÅÅ = t
@RD
Q2 m l2 t -1
2
III.
il campo induzione magnetica generato da una calamita è conservativo;
[falso] Il campo magnetico, in virtù del fatto che non ha cariche magnetiche, ovvero non può essere irrotazionale
e quindi non può essere conservativo.
IV.
il modulo del campo induzione magnetica generato da una carica in movimento è proporzionale su tutto lo
spazio all’inverso del quadrato della distanza;
Æ
Æ Æ
m
vâ r
1
Æ
Æ
Æ
[falso] B = ÄÄÄÄ
Ä0ÄÄÄ q ÄÄÄÄÄÄÄÄ
ÄÄÄÄ che va come ÄÄÄÄ
ÄÄ sempre tranne quando v e r sono paralleli, in quel caso Bº≡0 indipendent4p
r3
r2
Æ
emente dalla distanza r .
¶∂
[vero] infatti J spost = e0 ÅÅÅÅ
ÅÅ EHtL
¶∂ t
V.
la densità di corrente di spostamento è diversa da zero in presenza di un campo elettrico variabile nel tempo.
Ø
Ø












