Document

Capitolo 5
Strato Fisico- I mezzi trasmissivi
1
Bipoli
Bipolo: circuito elettrico che presenta due soli punti accessibili; può
essere attivo (generatore) oppure passivo (carico).
Segnali elettrici associati ad un bipolo: tensione ai capi, corrente
che lo attraversa.
i(t)
Ampère
bipolo attivo:
i(t)
bipolo passivo:
(generatore)
(carico)
v(t)
Volt
g(t)
v(t)
g(t)=tensione a vuoto
del generatore
Se i segnali di tensione e corrente sono impulsivi, o di energia
esistono le Trasformate di Fourier delle tensioni e delle correnti.
2
Esempi di Bipoli passivi
Si definisce impedenza Z(f) di un bipolo il rapporto
Z(f)= V(f) / I(f)
Esempi di bipoli passivi:
+
v(t)
+
i(t)
R (Ohm)
Resistore
v(t)=R i(t)
Z(f)=R
v(t)
-
+
i(t)
C (Farad)
Condensatore
i(t)=C dv(t)/dt
Z(f) = 1/( j2p f C)
v(t)
-
i(t)
L (Henry)
Induttore
v(t)=L di(t)/dt
Z(f) = j2p f L
3
Modello fisico di un collegamento
(1/2)
Trasmettitore
s(t)
g(t)
Mezzo trasmissivo
Z1(f)
gu(t)
Z2(f)
Ricevitore
r(t)
carico
Esempi di collegamenti rappresentati dal modello fisico:
s(t)
r(t)
4
Modello fisico di un collegamento
(2/2)
Il segnale ricevuto r(t) può differire dal segnale
trasmesso s(t) a causa di
  Distorsione di natura lineare
o Ritardo nel tempo
o Attenuazione di potenza
o Alterazioni della forma d’onda del segnale (filtraggio
di canale)
  Distorsione di natura non lineare
  Somma di disturbi di natura casuale (rumore)
  Somma di altri segnali indesiderati
5
Modello simbolico di un
collegamento
Segnale trasmesso s(t)
limitato in banda
da –B a B
S
Filtro di ricezione
passabasso
da –B a B
s(t)
E(f)
H(f)
r(t)
D
n(t)
WS
Potenza
Trasmessa
Canale
r(t) = s(t)*h(t)+n(t)*e(t)
Componente utile Componente di rumore
del segnale ricevuto, del segnale ricevuto,
di potenza WR
di potenza WN
6
Misure Logaritmiche Di Potenza
Wwatt Potenza assorbita: misurata in Watt
WmW Potenza assorbita: misurata in milliWatt
Misura logaritmica delle potenze:
dB riferito al Watt:
WdBW = 10 log10(Wwatt /1watt)
dB riferito al milliWatt:
WdBm = 10 log10(WmW /1mwatt)
Potenza in mW:
1
10
100
1000
Potenza in dBm:
0
10
20
30
Misura logaritmica di rapporto di potenze (numero puro):
R= W1/ W2 :
RdB = 10 log10 R
7
Attenuazione di un collegamento
(1/2)
 Supponiamo di trasmettere un segnale sinusoidale alla frequenza f0:
s(t)=A cos(2 p f0 t)
di potenza WS=A2/2.
 All’uscita di un canale LP con funzione di trasferimento H(f) la
componente utile del segnale ricevuto è ancora una sinusoide, scalata
in ampiezza di un fattore |H(f0)| e sfasata di 0=arg{H(f0)}:
|H(f0)| A cos(2 p f0 t+ 0)
di potenza WR= |H(f0)|2 A2/2.
 La potenza è ridotta di un fattore WS/ WR=1/|H(f0)|2
  Si definisce quindi attenuazione del collegamento A(f0) alla frequenza
f0 il valore
A(f0) = 1/|H(f0)|2
Baccarelli,
Cordeschi, Patriarca, Polli
8
Attenuazione di un collegamento
(2/2)
Misura logaritmica dell’ attenuazione del collegamento A(f0)
(Decibel):
AdB(f0) = 10 log10A(f0)
La potenza ricevuta è legata a quella trasmessa da:
WR dBm(f0) = WS dBm(f0) - AdB(f0)
(potenze misurate in
milliwatt)
ovvero
Calcoli:
watt)
WR dBW(f0) = WS dBW(f) - AdB(f0)
(potenze misurate in
WRdBW 10 log10(WR(f0)/1 w)
=10 log10(WS(f0) |H(f0)|2 /1 w)
=10 log10(WS(f0) /1 w) +10 log10( |H(f0)|2 )
= WSdBW –10Cordeschi,
log10(Baccarelli,
1/|Patriarca,
H(f0)|2Polli
)
9
Caratterizzazione del rumore
(1/2)
  Rumore di natura termica:
potenza WN (Watt) proporzionale alla larghezza di banda B(Hz) del
filtro di ricezione, ossia
WN=FKToB (watt)
dove F è il fattore di rumore del ricevitore (F1), K è la costante di
Bolzmann (K = 1.38x10-23 J / ° Kelvin) , To è la temperatura di lavoro del
ricevitore (To = 290° Kelvin).
  Ne deriva che il rapporto segnale-a-rumore a valle del filtro di
ricezione è
10
Caratterizzazione del rumore
(2/2)
Misura logaritmica del rumore:
WN dBm=F dB +KTo dBm/Hz+ BdBHz
FdB0 dB, KTo = -174 dBm/Hz e BdBHz =10log10BHz
11
Collegamenti mediante Linee in
Rame
rame
Isolante
Conduttore
interno
Conduttore esterno
(calza)
Doppino
(per segnali a banda
medio/piccola)
Cavo coassiale
(per segnali a banda
medio/alta)
Linea aerea
(in disuso per motivi
di costo)
12
Caratterizzazione delle Linee in
Rame (1/3)
Modello fisico di una linea in rame
Parametri caratteristici:
R = resistenza dei conduttori (Ohm/Km)
C = capacità tra conduttori (Farad/Km)
L = Induttanza dei conduttori (Henry/Km)
G = conduttanza tra conduttori (Mho/Km)
13
Caratterizzazione delle Linee in
Rame (2/3)
Attenuazione tipica di una linea alle basse frequenze
(qualche decina di kilohertz)
Baccarelli,
Cordeschi, Patriarca, Polli
14
Caratterizzazione delle Linee
in Rame (3/3)
Attenuazione tipica di un coassiale alle frequenze medio/alte
(decina di Megahertz)
Ao = 2,3 dB/Km @ 1MHz
15
Collegamenti Radio
Collegamento fisico
Terreno
Circuito equivalente
Segnale elettrico
di ingresso s(t)
A(f)
Segnale elettrico
di uscita r(t)
Attenuazione
16
Gamme di frequenza utilizzate
nelle TLC
Gamma
Nome
Sigla
servizio
0,3-300 kHz
Onde lunghe
LF
Radiolocalizzazione
marittima
300-3000 kHz
Onde medie
MF
Diffusione AM
3-30 MHz
Onde corte
HF
Collegamenti a
lunga distanza
30-300 MHz
Very high frequency
VHF
Radiomobili militari.
Diffusione FM
300-3000 MHz
Ultra High frequency
UHF
Ponti radio.
Diffusione televisiva
terrestre.
GSM.UMTS.
3-30 GHz
Super High
frequency
SHF
Ponti radio. Satelliti.
Radar.
17
Relazioni tra le potenze
Osservazione: la banda 2W occupata dal segnale modulato intorno
alla frequenza portante fp e’ piccola rispetto alle variazioni di
A(f). Quindi A(f) può ritenersi (circa) costante nella banda del
segnale modulato.
Relazione tra le potenze
fp
f
18
Guadagno d’antenna (1/7)
Supponiamo che un antenna trasmittente sia posta in O. Sia R un punto
di coordinate polari (d, ,  ) a distanza d (m) dall’antenna. La sfera su
cui giace R ha superficie 4πd2.
 Sia PTOT (Watt) la potenza totale irradiata dall’antenna.
 Sia PR =PR (d, ,  ), la quota parte della potenza irradiata
dall’antenna che transita attraverso una superficie di area S (m2)
centrata intorno ad R.
19
Guadagno d’antenna (2/7)
Definizione:
Un’antenna si dice isotropa se irradia la stessa quantità di
potenza in tutte le direzioni (, ) dello spazio con
-/2  /2, 0   2
 Quindi, se l’antenna trasmittente è isotropa abbiamo che
PR (d, ,  ) =PR (d)=(PTOT/4  d2) S
(Watt)
per ogni valore di , e di .
20
Guadagno d’antenna (3/7)
 Un’antenna trasmittente non isotropa distribuisce in modo non
uniforme la potenza irradiata nelle direzioni , .
o Sia PTOT (Watt) la potenza totale irradiata dall’antenna.
o Sia PR (d, ,  ), la quota parte della potenza irradiata
dall’antenna che transita attraverso una superficie di area S (m2)
centrata intorno ad un punto a distanza d, visto sotto le direzioni
,  . In generale PR (d, ,  ) differisce dal valore
PTOT/(4  d2) S corrispondente al caso di antenna trasmittente
isotropa.
21
Guadagno d’antenna (4/7)
Guadagno d’antenna G(, ) la
funzione
  Si dice
G ( ,  )  PR (d, ,  ) / [PTOT/(4  d2) S]
(Watt)
-/2  /2, 0   2
che descrive il modo in cui un’antenna
trasmittente irradia la potenza nelle varie
direzioni ( , ) dello spazio.
22
Guadagno d’antenna (5/7)
Il Guadagno d’antenna G(, ) gode delle seguenti proprietà:
 È una funzione non negativa
G ( ,  )  0,  ,  ;
 Un’antenna isotropa presenta un guadagno costante in tutte le
direzioni,
G ( ,  ) =1,  ,  ;
 Un’antenna si dice direttiva nella direzione 0,  0 se presenta un
guadagno molto grande nella direzione 0,  0 , ossia se
G (0,  0 ) >>1 e G (,  ) <<1 altrove
 Tipicamente il guadagno d’antenna è espresso in unità logaritmiche (dB)
G( , ) (dB) =10 log
10
(G( , ) ).
23
Guadagno d’antenna (6/7)
  Si
definisce come solido d’irradiazione di un’antenna con
guadagno G(, ) (dB) la superficie tridimensionale ottenuta
riportando per ogni direzione (, ) un segmento
proporzionale a G(, ) (dB)
  Quindi il solido d’irradiazione è la rappresentazione grafica
del guadagno G(, ) (dB)
24
Guadagno d’antenna (7/7)
Le antenne direttive possono essere classificate secondo la forma
assunta dal solido di irradiazione:
Antenne fortemente direttive possono presentare valori del
guadagno d’antenna G(dB) anche dell’ordine di 50 dB nella direzione
preferenziale (0, 0).
25
Area efficace di un’antenna
ricevente (1/3)


Supponiamo che un antenna ricevente sia posta in O. Supponiamo che
incida sull’antenna un’onda e.m. proveniente dalla direzione (,  ).
o Sia PR (Watt) la potenza totale captata dall’antenna.
o Sia pI (,  ) (Watt/m2) la densità superficiale di potenza convogliata
dall’onda incidente sull’antenna.
26
Area efficace di un’antenna
ricevente (2/3)
 Si dice Superficie efficace d’antenna SE(, )
la funzione
SE ( ,  ) = PR / pI (,  ) (m2)
-/2  /2, 0   2
che descrive il modo in cui un’antenna ricevente
capta la potenza incidente dalle varie direzioni ( ,
) dello spazio.
27
Area efficace di un’antenna
ricevente (3/3)
  Una stessa antenna può operare
indifferentemente come ricevente o
trasmittente. Sussiste il seguente legame fra
il guadagno di un‘antenna e la sua superficie
efficace:
SE ( ,  ) = G ( ,  ) λ2 / 4p
  dove λ =c/f è la lunghezza d’onda dell’onda
e.m. irradiata/captata dall’antenna, a sua volta
legata alla frequenza f dalla relazione λ =c/f,
con c=3 x108 m/s (velocità della luce nel
vuoto).
28
Attenuazione di spazio libero
(1/2)
q’
d

j’

29
Attenuazione di spazio libero
(2/2)
Misura logaritmica dell’attenuazione introdotta dal collegamento:
Attenuazione dello spazio libero
L’attenuazione introdotta dal collegamento dipende da
 la distanza fra le antenne
 dalla frequenza portante utilizzata
 il guadagno dell’antenna trasmittente (attitudine dell’antenna
trasmittente ad amplificare il segnale trasmesso nella direzione del
collegamento)
 il guadagno dell’antenna ricevente (attitudine dell’antenna ricevente ad
captare il segnale ricevuto nella direzione del collegamento).
30
Fibra Ottica: caratteristiche
fisiche (1/4)
Imposs
ibile
visuali
zzare
l'imma
gine.
La
memor
ia del
compu
ter
potreb
 Una fibra ottica è costituita da un cilindro
dielettrico (cuore, o core) circondato
esternamente da una corona circolare (mantello, o
cladding) costituita da un altro materiale
dielettrico.
31
Fibra Ottica: caratteristiche
fisiche (2/4)
  Le grandezze fisiche e i parametri geometrici
che caratterizzano la fibra sono:
– 
– 
– 
– 
a raggio del cuore (m)
b raggio esterno del mantello (m)
n1 = c / v1 indice di rifrazione del cuore
n2 = c / v2 indice di rifrazione del mantello
dove c=3 x108 m/s rappresenta la velocità
della luce nel vuoto, v1 la velocità della luce nel
cuore, v2 la velocità della luce nel mantello.
32
Fibra Ottica: caratteristiche fisiche
(3/4)
Imposs
ibile
visualiz
zare
l'imma
gine.
La
memor
ia del
comput
er
potreb
Una fibra ottica impiegata come mezzo trasmissivo tra una sorgente ed
una destinazione di un collegamento di telecomunicazioni opera sotto le
seguenti condizioni:
n1 >n2 , b>>a
Tipicamente, si ha
 b 10 a
 n11.01 n2
 a 2.4 l / (2p
)
(condizione di monomodo)
dove l(m) è la lunghezza d’onda della radiazione luminosa che viaggia nella
fibra.
33
Fibra Ottica: caratteristiche
fisiche (4/4)
 
Impossi
bile
visualizz
are
l'immagi
ne. La
memori
a del
compute
r
potrebb
e essere
insuffici
ente per
aprire
l'immagi
ne
oppure
l'immagi
ne
potrebb
e essere
Sia  l’angolo di incidenza del raggio luminoso rispetto alla normale alla
superficie di separazione cuore/mantello. Se è verificata la condizione
di riflessione totale
allora il raggio luminoso incidente alla superficie di separazione cuore/
mantello è totalmente riflesso all’interno del cuore e il raggio luminoso si
propaga lungo l’asse della fibra, subendo, eventualmente, riflessioni
multiple.
34
Collegamenti in Fibra Ottica
Circuito fisico
Impossibil
e
visualizza
re
l'immagin
e. La
memoria
del
computer
potrebbe
essere
insufficien
te per
aprire
l'immagin
e oppure
l'immagin
Impossibil
e
visualizza
re
l'immagin
e. La
memoria
del
computer
potrebbe
essere
insufficien
te per
aprire
l'immagin
e oppure
l'immagin
Circuito equivalente
Baccarelli,
Cordeschi, Patriarca, Polli
35
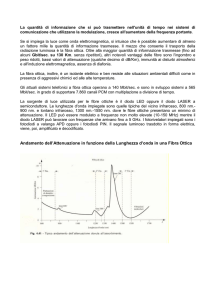
Caratteristiche di attenuazione di
una fibra
La luce emessa ha uno spettro di emissione molto stretto, centrato
intorno ad una lunghezza d’onda compresa tra 0,8 e 1,8 micron.
L’attenuazione in dB/km presenta un minimo in corrispondenza di
alcuni intervalli di lunghezze d’onda (finestre).
36
Caratteristiche di dispersione
temporale in una fibra (1/3)
 Dispersione
temporale: un impulso luminoso applicato all’ingresso
si presenta in uscita con una durata temporale maggiore
potenza
ottica
 Dispersione
modale: Se il cuore della fibra ha un raggio a
“elevato” si verificano più modalità di propagazione (modi),
ciascuno dotato di diversa velocità di propagazione. Per evitare
questa dispersione
o si usano fibre di piccolo diametro, chiamate MONOMODO
37
Caratteristiche di dispersione
temporale in una fibra (2/3)
  Dispersione
cromatica: Il diodo generatore
distribuisce l’energia luminosa su più
lunghezze d’onda, λ1,λ2,.. aventi diversa
velocità di propagazione. Il fenomeno è molto
poco sensibile in seconda finestra. Per ridurre
questa dispersione
– si usano sorgenti a banda molto stretta,
quasi monocromatiche (LASER invece che
LED)
38
Caratteristiche di dispersione
temporale in una fibra (3/3)
 La dispersione temporale D (sec.) è proporzionale alla lunghezza del
collegamento in accordo a
dove, per il caso di sola dispersione cromatica t = 0,06 nsec/Km per
i laser e t = 2,5 nsec/Km per i led.
 La massima dispersione tollerabile è (2 t dkm)  Tbit
 Quindi la Massima frequenza binaria fb utilizzabile, per un
collegamento di dKm è
Baccarelli,
Cordeschi, Patriarca, Polli
39
Caratteristiche di impiego di una
fibra
Le fibre attualmente impiegate sono monomodo, e dunque
presentano solo dispersione cromatica. Si utilizza la terza finestra.
 minore attenuazione, dell’ordine di 0,25 dB/Km
 maggiore dispersione cromatica , dell’ordine di t = 0,06 nsec/Km
per i laser, e di t = 2,5 nsec/Km per i led
Frequenze binarie di trasmissione
raggiungibili in una fibra monomodo, in
terza finestra.
Baccarelli,
Cordeschi, Patriarca, Polli
40
Caratteristiche dei fotorivelatori
(1/2)
All'uscita della fibra ottica è applicato un diodo fotorivelatore che, investito
dalla luce in uscita dalla fibra, genera una corrente elettrica il cui valor medio
im (ampere) è proporzionale al valore della potenza luminosa incidente in
accordo a
im=mg r WR
dove WR (watt) è la potenza ottica ricevuta,
r è la responsività del fotodiodo
(valore tipico 0.5 Ampère/Watt), mg è il fattore di fotomoltiplicazione, e
dipende dal tipo di diodo utilizzato. In un diodo PIN ogni fotone produce una
coppia elettrone-lacuna e quindi mg=1. In un diodo APD per effetto valanga
ogni fotone produce in media mg coppie,
con mg >1.
Baccarelli,
41
Cordeschi, Patriarca, Polli
Caratteristiche dei fotorivelatori
(2/2)
 Sovrapposte al segnale utile im=mg r WR sono presenti in
uscita due componenti di rumore, il rumore quantico iq(t) e il
rumore termico in(t) in accordo alla:
i(t)= mg r WR
+ iq(t)+in(t)
  La potenza del rumore quantico iq(t) aumenta all’aumentare di WR e di
mg mentre la potenza di in(t) non varia al variare di WR e mg
Corrente all'uscita del
fotorivelatore per due diversi valori
della potenza ottica incidente WR.
42
Rapporto segnale/rumore in una
fibra (1/2)
 Il rapporto segnale/rumore quantico SNRQ
o Cresce al crescere della potenza ottica ricevuta WR
o Decresce al crescere del guadagno di fotomoltiplicazione mg
 Il rapporto segnale/rumore termico SNRT
o Cresce al crescere della potenza ottica ricevuta
o Cresce al crescere del guadagno di fotomoltiplicazione mg
43
Rapporto segnale/rumore in una
fibra (2/2)
 Caso di “bassa” potenza ricevuta (ad esempio in uscita da un
collegamento in fibra molto lungo)
o Il rapporto segnale rumore complessivo é principalmente
limitato dalla presenza di rumore termico
o In tal caso é opportuno utilizzare un diodo APD, con guadagno
di fotomoltiplicazione mg>1.
 Caso di “alta” potenza ricevuta
o Il rapporto segnale rumore complessivo é principalmente
limitato dalla presenza di rumore quantico
o In tal caso é opportuno utilizzare un diodo PIN, con guadagno
di fotomoltiplicazione mg=1.
44