Materiali magnetici

Materiali magnetici
B = vettore induzione magnetica
H = vettore intensità del campo magnetico
nel vuoto:
B = μo H
La costante μo è la permeabilità magnetica del vuoto:
6 H/m
μo = 1,26
1 26 10-6
In presenza di un qualunque materiale:
B = μr μoH
μr = permeabilità relativa del materiale.
μr < 1, per materiali diamagnetici.
μr > 1, per materiali paramagnetici.
μr >> 1, per materiali ferromagnetici e ferrimagnetici.
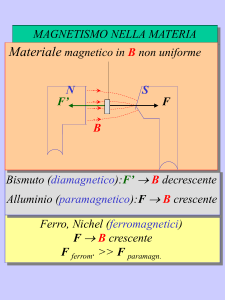
Materiali magnetici
Materiali diamagnetici
Il campo magnetico viene indebolito all’interno del materiale (μr circa
1) In un materiale diamagnetico non esistono dipoli magnetici
1).
permanenti. l’applicazione di un campo magnetico di induzione B
crea dei dipoli magnetici di direzione opposta e quindi tali da
indebolire B.
B
Materiali paramagnetici
Il campo magnetico viene rafforzato all’interno del materiale. l’effetto
è piuttosto debole (μr circa 1).
Nei
materiali
paramagnetici
sono
presenti
dipoli
magnetici
permanenti di tipo
p
p atomico:
•
Per B = 0 i dipoli non hanno una direzione preferenziale;
•
Per B ≠ 0
i dipoli tendono ad orientarsi nella direzione del
p rafforzandolo.
campo
Materiali magnetici
M t i li ferromagnetici
Materiali
f
ti i
Si ha un effetto simile a quello dei materiali paramagnetici ma molto
rafforzato (μr dell’ordine di alcune migliaia o decine di migliaia).
I dipoli permanenti sono raggruppati in
domini ( domini di Weiss) i cui momenti B
ROTAZIONE DEI
MOMENTI MAGNETICI
B
magnetici non sono concordi fra loro
per valori nulli o molto bassi di B.
Se B cresce aumentano le dimensioni
CRESCITA DEI DOMINI
CONCORDI.
CONTRAZIONE DEI
DOMINI DISCORDI
dei domini concordi con il campo e si
ha la rotazione di altri domini.
H
Materiali ferromagnetici
Curva di prima magnetizzazione di un materiale
La curva di prima magnetizzazione è il diagramma di B in funzione di H di un provino di materiale mai
magnetizzato
in
sperimentalmente.
precedenza
precedenza.
La
curva
di
prima
magnetizzazione
può
essere
determinata
Materiali ferromagnetici
Ciclo di isteresi
Il fenomeno dell’isteresi in un materiale ferromagnetico si può spiegare con il fatto che per B = 0 non tutti i
d i i ritornano
domini
it
all’orientamento
ll’ i t
t iniziale.
i i i l
L’isteresi magnetica produce delle perdite la cui entità è proporzionale all’area del ciclo.
Materiali ferromagnetici dolci
B
SONO CARATTERIZZATI
DA:
Materiali ferromagnetici duri
SONO CARATTERIZZATI
DA:
B
z BASSA μmax
z ELEVATA μ max
H
z ELEVATA B r
z BASSO H c
z PICCOLA AREA DEL
H
z ELEVATA Hc
z GRANDE AREA DEL
CICLO
CICLO
Nuclei ferromagnetici
Magneti permanenti
Materiali ferromagnetici
Perdite per isteresi
In presenza di un campo variabile è necessario fornire energia per consentire le continue variazioni di
orientamento dei domini. L’energia per unità di volume necessaria per portare un materiale all’induzione B
vale:
B
Wi = ∫ HdB
0
Seguendo un intero ciclo di magnetizzazione viene dissipata una quantità di energia per unità di volume
pari all’area del ciclo d’isteresi.
d’isteresi
In pratica per determinare la potenza perduta per isteresi pi si usa la formula di Steinmetz:
pi = ki f BMh
• ki = costante del materiale
materiale.
• BM = valore massimo di B.
• h = 1,6 - 2,2 crescente con B
MATERIALI FERROMAGNETICI
Perdite per correnti parassite
Sono prodotte da correnti che, nella massa di un conduttore ferromagnetico, circolano su
piani ortogonali alla direzione del vettore B, variabile nel tempo.
B
i
Le perdite per correnti parassite valgono:
pc = kc f2 BM2
f = frequenza di B
kc = costante caratteristica del materiale
BM = valore massimo di B.
Poiché kc dipende dalla resistività ρ del materiale e dalla sezione S perpendicolare alla
direzione di B, per ridurre pc è necessario aumentare ρ e ridurre S.
Materiali ferromagnetici
Perdite totali
Le perdite totali in un materiale ferromagnetico sono pari a:
h
pf = pi + pc = ki f BM + kc f 2 BM
2
Spesso, per un valore fissato di frequenza, si può anche porre con buona approssimazione:
pf = kf B M 2
Perdite totali a 20-25-50-60-120-150-180-250-300-350-420-550-660-780-950 Hz
Materiali ferromagnetici
Perdite totali
Mediante l’apparecchio di Epstein è possibile misurare le perdite totali e non singolarmente
le perdite per isteresi e correnti parassite. Dividendo le perdite totali per la frequenza si ha:
h
W f = W i + W c = ki BM + kc f BM
2
Materiali ferromagnetici
Cifra di perdita
Nella pratica il valore delle perdite di un materiale ferromagnetico viene fornito attraverso la
cifra di perdita pm così definita:
pm = Potenza perduta in un chilogrammo di materiale (espressa in W/kg) con
B = 1 T, f = 50 Hz,
Se G è il peso del materiale soggetto all
all’induzione
induzione di 1 T le perdite valgono:
Pm = k pmG
(W)
dove k > 1 tiene conto del fatto che nella p
pratica le p
perdite del materiale ferromagnetico
g
in una
macchina elettrica sono superiori di un 20÷30% rispetto a quelle misurate con l’apparecchio di
Epstein sul provino a causa delle differenti condizioni di lavoro del materiale.
Per B≠ 1, in prima approssimazione:
Pm = k pmG B2
(W)
Per un calcolo più preciso occorre usare un diagramma delle perdite in funzione di B.
Materiali ferromagnetici
Riduzione delle perdite per isteresi
• Riduzione dell’area del ciclo d’isteresi - Si ottiene agendo sulla composizione del materiale (leghe Fe-Si)
e attraverso trattamenti di ricottura.
Riduzione delle perdite per correnti parassite
• Aumento della resistività del materiale – Si ottiene modificando la composizione del materiale
(aumentando il tenore di silicio)
• Introduzione di discontinuità elettriche - Si ottiene utilizzando lamierini isolati dello spessore di 0,5 0,35 mm posti in modo da opporsi alla circolazione delle correnti parassite.
i
B
Materiali ferromagnetici
L i i i in
Lamierini
i Fe-Si
F Si a cristalli
i t lli non orientati
i t ti
Si tratta di lamierini di acciaio con aggiunta di silicio fino ad un massimo del 4 - 4,5 %. L’aggiunta di silicio
produce i seguenti vantaggi:
• Aumenta fortemente la resistività.
• Diminuisce leggermente le perdite per isteresi.
• Aumenta la permeabilità massima. Si ha infatti:
− μr = 5000 per un acciaio allo 0,2% C
− μr = 7000 per un acciaio al 3% Si
Svantaggi prodotti dall’aggiunta di silicio:
• Diminuisce leggermente Bs (circa 2 T)
• Diminuisce la conducibilità termica
• Aumenta la fragilità
I lamierini a cristalli non orientati hanno caratteristiche magnetiche isotrope e possono essere utilizzati per
realizzare sia trasformatori che macchine rotanti.
Materiali ferromagnetici
Lamierini in Fe
Fe-Si
Si a cristalli orientati
Con ripetute laminazioni a freddo intervallate da trattamenti di ricottura si ottengono lamierini in cui i
domini hanno i momenti magnetici concordemente orientati nella direzione di laminazione .
Si ottengono lamierini con:
• cifra di perdita inferiore a 0,75 W/kg (0,4 - 0,6 W/kg).
• elevata
l
permeabilità
bili à (μ
( max = 30.000,
30 000 μi = 1.500).
1 00)
• Induzione di saturazione leggermente superiore a quella dei lamierini a cristalli non orientati (Bs = 2 T)
0o
μr
55o
pm
90o
Materiali ferromagnetici
I lamierini a cristalli orientati sono impiegati in tutti quei circuiti magnetici nei quali il flusso abbia una
direzione prevalente, cioè:
• nei nuclei dei trasformatori
• nelle espansioni polari delle dinamo.
I lamierini a cristalli orientati sono disponibili in rotoli alti 1m. la loro superficie è isolata e può essere
successivamente verniciata, dopo tranciatura viene effettuato un trattamento di ricottura.
GIUNTI A 45o E A 90o
B
B
B
B
Materiali ferromagnetici
Ferriti
Sono materiali non metallici costituiti da ossidi di ferro e di un metallo bivalente (Mg, Mn, Zn, Cu, .....) ed
assimilabili a materiali ceramici dei quali hanno la durezza e la fragilità.
fragilità
Hanno conducibilità molto bassa e quindi perdite molto ridotte e qundi adatte alla realizzazione di nuclei
ferromagnetici per applicazioni in alta frequenza (5 – 500 kHz).
kHz)
Le ferriti più comuni sono del tipo Mn - Zn, Ni - Zn, Mg - Mn.
0,4
B (T)
Zn - M n
N i - Zn
,
0,3
0,2
Mg - Mn
01
0,1
H (As/m )
100
200
300
Materiali isolanti
I materiali isolanti o dielettrici, hanno la funzione di separare parti a potenziale diverso e di
obbligare la corrente a seguire determinati percorsi.
Si definisce dielettrico un materiale isolante elettrico perfetto (idealmente) o debolmente conduttore
(dielettrico con perdite) con resistività superiore a 109 - 1010 Ωm.
L corrente
La
t I che
h attraversa
tt
un dielettrico
di l tt i reale,
l non è in
i quadratura
d t
con la
l tensione
t
i
V ma forma
V,
f
un
angolo minore di π/2, tanto più piccolo quanto maggiori sono le perdite, di cui si tiene conto con
una resistenza R.
_
_
_
_
I = Ic + IG = (jωC + 1/R) V
R
Le perdite negli isolanti risultano trascurabili rispetto alle perdite globali di una macchina elettrica.
Materiali isolanti
Scarica in un materiale isolante
Aumentando progressivamente il valore della tensione V e del
campo elettrico E si ha un aumento della corrente. Superato un
valore di soglia (Vs, Es) si produce però una scarica disruptiva cioè
un improvvisa trasformazione del materiale isolante in conduttore.
Per un dielettrico di spessore "d" in condizioni di campo uniforme
si ha alla scarica:
ES = VS/d
Es è detto rigidità dielettrica. La tensione di scarica, a parità di distanza elettrodica, diminuisce
tanto p
più quanto
q
più
p aumenta la disuniformità del campo
p elettrico.
parziali,, che interessano cioè solo una
Possono verificarsi scariche p
parte dello spessore dell’isolamento e che non provocano
necessariamente scarica totale, pur danneggiando in generale
l isolamento.
l’isolamento.
Materiali isolanti
Invecchiamento degli isolanti
L’invecchiamento di un materiale è il peggioramento irreversibile di una o più proprietà del
materiale stesso causata da una o più sollecitazioni esterne,
In tensione alternata è possibile che dopo alcune migliaia di ore di lavoro si verifichi la perforazione
dell’isolamento in corrispondenza di valori di tensione molto inferiori al valore che causa la scarica
istantanea.
Vita degli isolanti
La vita è il periodo di tempo atteso prima che la proprietà di un materiale o di un apparato,
sottoposto a determinate sollecitazioni, raggiunga un valore minimo prefissato. La vita dipende dal
ti
tipo
di sollecitazioni
ll it i i applicate
li t e dal
d l loro
l
valore.
l
Sollecitazioni sugli isolanti:
• termiche
• dielettriche
• meccaniche
Materiali isolanti
Effetti della temperatura sull
sull’invecchiamento
invecchiamento
L’aumento di temperatura accelera le reazioni chimiche che presiedono alla degradazione del
materiale. In p
particolare,, si riduce la rigidità
g
dielettrica.
L’equazione di vita termica è del tipo:
logn d =
E
+a
kθ
E = energia di attivazione della reazione
θ = temperatura assoluta in gradi Kelvin
k = costante di Boltzman
a = costante del materiale
Un aumento di 10 °C della temperatura di esercizio produce all’incirca il dimezzamento
della durata di vita del dielettrico
Materiali isolanti
Classi di temperatura
I materiali isolanti vengono raggruppati secondo varie classi di temperatura. L’appartenenza del
materiale ad una data classe determina la temperatura di servizio del sistema di isolamento.
CLASSE TERMICA TEMPERATURA °C
MATERIALE DI RIFERIMENTO
Y
90
Carta, cartone, seta,fibre poliammidiche.
A
105
Acetato di cellulosa, carta impregnata con olio
minerale.
E
120
Resine
R
i poliestere,
li t
smalti
lti poliuretanici
li
t i i ed
d
epossidici.
B
130
Isolamenti micati con impregnante asfaltino.
F
155
Isolamenti micati con impregnante
termoindurente.
H
180
Isolamenti siliconici.
Materiali isolanti
Dall’equazione di vita dei materiali isolanti si ricavano le rette di vita, che riportano la durata della
vita utile degli isolanti in funzione della temperatura.
La scala dei tempi è logaritmica,
logaritmica e il valore di 105 rappresenta,
rappresenta ad esempio
esempio, la durata di 34 anni
anni.
Basandosi su queste curve si fa in modo che la vita media probabile di una macchina sia di circa 30
anni.
Materiali isolanti
Eff tti d
Effetti
della
ll ttensione
i
applicata
li t sull’invecchiamento
ll’i
hi
t
Per descrivere l’invecchiamento elettrico in corrente alternata, si può usare la legge:
lognd = c - m logne
dove:
d = Durata della vita del materiale
e = valore efficace del campo elettrico
c ed m = costanti del materiale.
Materiali isolanti
Effetti delle scariche par
parziali
iali sull’invecchiamento
s ll’in ecchiamento
In presenza di inclusioni gassose
nell’isolamento possono verificarsi scariche parziali, che
interessano cioè solo una parte dello spessore dell
dell’isolamento
isolamento e che non provocano scarica totale,
ma producono invecchiamento (erosione) del materiale isolante.
In corrente alternata il numero delle scariche parziali nell’unità di tempo e quindi l’entità del danno
prodotto, dipende dalla frequenza di alimentazione.
Materiali isolanti
Prove d’invecchiamento accelerato
Per simulare in modo accelerato l’invecchiamento
l invecchiamento e quindi per stimare la vita di un isolante si utilizza il
principio delle sollecitazioni equivalenti, sfruttando il modello d’invecchiamento.
Aumentando la tensione applicata si possono ottenere in tempi ridotti sollecitazioni equivalenti a quelle
generate da tensioni inferiori per tempi molto più lunghi.
Una tecnica analoga può essere adottata anche per gli stress termici
Materiali isolanti
Prove d’isolamento
Scopo delle prove d’isolamento sulle macchine elettriche è quello di verificare mediante prove di
breve durata se la macchina è in grado di sostenere le sollecitazioni elettriche cui sarà sottoposta
durante il funzionamento.
Sollecitazioni elettriche durante il servizio:
• a tensione e frequenza nominali.
nominali
• a frequenza superiore alla nominale.
• sovratensioni impulsive dovute a manovre di apertura e chiusura di interruttori (2÷4 volte la
t
tensione
i
nominale
i l con tempi
t
i di salita
lit di centinaia
ti i di μs e tempi
t
i all’emivalore
ll’ i l
di migliaia
i li i di μs).
)
• sovratensioni di origine atmosferica (3÷5 volte la tensione nominale con tempi di salita di
qualche μs e tempi all’emivalore di decine di μs).
Materiali isolanti
Prove
o e d
di isolamento
so a e to esterno
este o
(isolamento tra avvolgimenti e
parti collegate a massa) - Durata
prova 60s con tensione di
della p
prova
pari
tensione
al
doppio
nominale
o,
della
per
macchine di bassa tensione, a
due volte la tensione nominale
più 1000 V.
Prove di isolamento interno
(isolamento tra spira e spira) Durata della prova 5 minuti per
le macchine rotanti, e 6000 cicli
per i trasformatore con tensione
di prova pari a 1.5 volte la
tensione nominale.
Materiali isolanti
Prova all’impulso
p
Consiste nel simulare una fulminazione atmosferica per tre volte di seguito con un gradino di
tensione, che si ottiene con la carica e scarica di un condensatore.
Forma d’onda della sollecitazione impulsiva (Vmax corrisponde a 4 Vn).
Materiali isolanti
Nelle condizioni di prova il trasformatore può essere rappresentato
come un semplice circuito elettrico con due capacità (le capacità
parassite tra spira e spira e tra spira e massa) ed un’impedenza
ohmco-resistiva.
Nei primi istanti del transitorio l’induttanza non è attraversata da
corrente, quindi la macchina si comporta come un condensatore.
Il trasformatore durante la prova può essere
rappresentato mediante Il condensatore C, che
si carica attraverso la resistenza Rf e si scarica
attraverso la serie Rc+Rf. ≈ Rc.
Poiché Rc>>Rf. La scarica è molto più lenta
della carica, producendo il profilo di tensione
specificato.
Materiali isolanti
Isolamento dei lamierini ferromagnetici
Coefficiente di stipamento kST =
Sezione netta del nucleo (ferro)
Sezione lorda del nucleo (ferro + isolante)
Materiale
kST
Utilizzo
Carta
.85÷.9
Macchine rotanti
Vernici
T
Trattamenti
i chimici
hi i i (fosfatazione)
(f f
i
)
.88÷.93 Macchine rotanti e trasformatori
.9÷.96
9 96
trasformatori
f
i