Prova finale

Possibile prova finale
1.
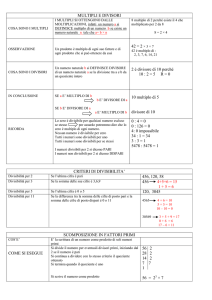
Cos’è il minimo comune multiplo 1 tra più numeri assegnati?
Contrassegnare la risposta giusta:
 un qualsiasi multiplo dei numeri assegnati
 il più piccolo multiplo dei numeri assegnati
 il più piccolo multiplo comune a tutti i numeri assegnati
2.
Come si trova il minimo comune multiplo tra più numeri ?
Contrassegnare la risposta giusta:
 Si moltiplicano tra loro i numeri dopo averli scomposti in fattori primi
 Dopo aver scomposti i numeri in fattori primi si moltiplicano tra loro i fattori comuni
 Dopo aver scomposti i numeri in fattori primi si moltiplicano tra loro i fattori comuni e non comuni
 Dopo aver scomposti i numeri in fattori primi si moltiplicano tra loro i fattori comuni e non comuni col
massimo esponente
Vedi teoria ed esempi nelle note a fine pagina su Minimo comune multiplo 2
3.
Cos’è il Massimo Comune Divisore 3 tra più numeri assegnati?
Contrassegnare la risposta giusta:
 un qualsiasi divisore dei numeri assegnati
 il più grande divisore dei numeri assegnati
 il più grande divisore comune a tutti i numeri assegnati
4.
Come si trova il Massimo Comune Divisore tra più numeri ?
Contrassegnare la risposta giusta:
 Scompongo i numeri in fattori primi e prendo i fattori comuni
 Scompongo i numeri in fattori primi e prendo i fattori comuni e non comuni
 Scompongo i numeri in fattori primi e prendo i fattori comuni col minimo esponente
Vedi teoria ed esempi nelle note a fine pagina su Massimo Comune Divisore4
5.
Per ridurre una frazione ai minimi termini o “semplificare” cosa occorre?
Contrassegnare la risposta giusta:
 Trovare il Massimo Comune Divisore del numeratore e del denominatore
 Trovare il minimo comune multiplo del numeratore e del denominatore e dividere ciascuno per lo
stesso
 Trovare il Massimo Comune Divisore del numeratore e del denominatore e dividere ciascuno di
essi per lo stesso
Vedi teoria ed esempi nelle note a fine pagina5
6.
Per sommare più frazioni numeriche tra loro occorre renderle omogenee, cioè ridurle ad uno stesso
denominatore. Come occorre procedere?
Contrassegnare la risposta giusta:
 Occorre trovare il minimo comune multiplo tra i denominatori delle frazioni
 Occorre trovare il Massimo Comune Divisore tra i numeratori
 Occorre trovare il minimo comune multiplo tra i denominatori delle frazioni rendendole omogenee
e sommare infine le frazioni rese omogenee.
Vedi teoria ed esempi nelle note a fine pagina6.
7.
La retta y = -1 a quale dei tre grafici sottostanti corrisponde 7 ? Contrassegnare la risposta giusta:
 Fig. 1
 Fig. 2
 Fig. 3
8.
giusta:



9.
10.
La retta 3∙y = - 2 ∙ x + 4 a quale dei tre grafici sottostanti corrisponde 8? Contrassegnare la risposta
Fig. 1
Fig. 2
Fig. 3
La retta y = - 2 ∙ x + 3 a quale retta è parallela? Contrassegnare la risposta giusta 9:
 Alla retta y = 2 ∙ x - 5
 Alla retta y = - 2 ∙ x - 5
 Alla retta y = 3 ∙ x - 2
Nella figura sottostante è riportato un polinomio. Contrassegnare i punti corrispondenti alle radici 10.
 Sono i punti in cui il diagramma del polinomio interseca l’asse x
 Sono i punti in cui il diagramma del polinomio interseca l’asse y
1 (la risposta è la terza) minimo comune multiplo in base alla definizione
Dati più numeri (es.) 2; 9;12 trovare il minimo comune multiplo in base alla definizione
Cerco tutti i multipli di 2 ; 9 ; 12 :
1) 2 ; 4; 6; 8; 10; 12; 14; 16; 18; 20; 22; 24; 26; 28; 30; 32; 34; 36; 38; …; 72; ….; 108; …
2) 9; 18; 27; 36; 45; 54; 63; 72; 81; 90; 99; 108; ….
3) 12; 24; 36; 48; 60; 72; 84; 96; 108; ….
Individuo quelli comuni ai numeri dati (sono quelli in grassetto), e di questi prendo il più piccolo. Quindi 36 è il m. c. m.
2 (la risposta è la quarta) trovare il minimo comune multiplo è equivalente a scomporre i numeri dati in fattori primi
1) 2 = 2 1
2) 9 = 3 2
3) 12 = 2 2 · 3
prendere i fattori primi comuni e non comuni col massimo esponente (sono quelli in grassetto) e li moltiplico tra loro
m. c. m. = 2 2 · 3 2 = 4 · 9 = 36
3 (la risposta è la terza) Dati più numeri (es.) 72; 99;120 trovare il Massimo Comune Divisore in base alla definizione
Cerco tutti i divisori di 72 ; 99 ; 120 :
1) 72 :
2; 3; 4; 6; 8; 9; 12; 18; 24; 36; 72;
2) 99 :
3; 9; 11; 33; 99;
3) 120 :
2; 3; 4; 5; 6; 8; 10; 12; 15; 20; 24; 30; 40; 60; 120;
Individuo quelli comuni ai numeri dati (sono quelli in grassetto), e di questi prendo il più grande. Quindi 3 è il Massimo
Comune Divisore.
4 (la risposta è la terza) trovare il Massimo Comune Divisore è equivalente a scomporre i numeri dati in fattori primi
1) 72 = 2 3 · 3 2
2) 99 = 3 2 · 11
3) 120 = 2 3 · 3 · 5
prendo solo i fattori primi comuni col minimo esponente in questo caso è 3 1.Quindi il M. C. D. = 3 .
La risposta è la terza. Esempio 45 / 225. Tra 45 = 3 2 ∙ 5 e 225 = 3 2 ∙ 5 2 il Massimo Comune Divisore è 3 2 ∙ 5 = 45,
divido quindi numeratore e denominatore per esso ed ottengo che 45 / 225 = 1 / 5
5
6
La risposta è la terza. Esempio
2 5 4
  .
3 2 9
Il minimo comune multiplo tra i denominatori è 18.
7
2 5 4 12 45 8 12  45  8 65
  




3 2 9 18 18 18
18
18
La risposta è la seconda
La risposta è la seconda
9
La risposta è la seconda
10
La risposta è la prima ( i punti in cui il diagramma del polinomio interseca l’asse x).
8