Unità di misura (SI)
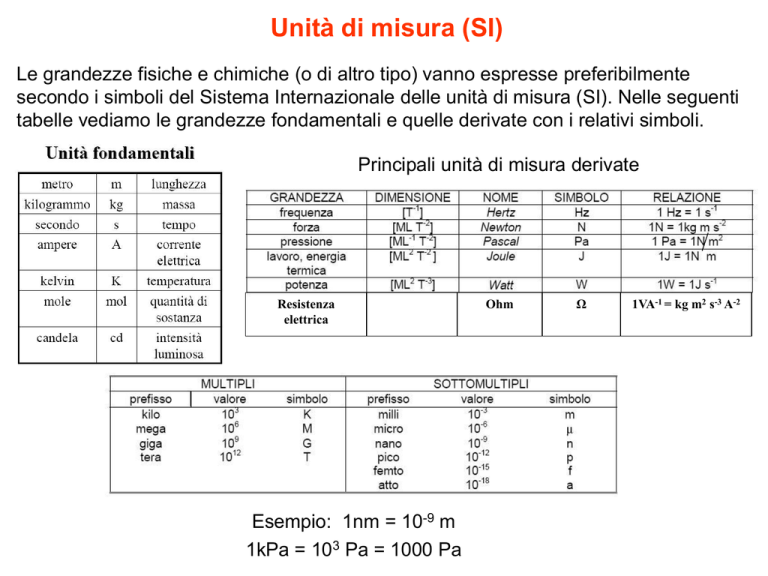
Le grandezze fisiche e chimiche (o di altro tipo) vanno espresse preferibilmente
secondo i simboli del Sistema Internazionale delle unità di misura (SI). Nelle seguenti
tabelle vediamo le grandezze fondamentali e quelle derivate con i relativi simboli.
Principali unità di misura derivate
Resistenza
elettrica
Esempio: 1nm = 10-9 m
1kPa = 103 Pa = 1000 Pa
Ohm
Ω
1VA-1 = kg m2 s-3 A-2
Proprietà generali: Densità
La densità di un materiale è definita come la massa per unità di volume:
Densità = ρ = m / V
m = massa [kg o g]
unità di misura [kg/dm3 o g/cm3]
V = volume [dm3 o cm3]
La densità dei materiali è strettamente legata al numero atomico degli elementi
che li costituiscono e al modo in cui gli atomi e le molecole si dispongono nello
spazio (struttura).
N.B. Il numero atomico indica il numero di protoni all'interno del nucleo di un
atomo (vedi tavola periodica degli elementi). La massa di un atomo è quasi
tutta concentrata nel nucleo (protoni e neutroni).
Materiale
Acciaio
Alluminio
Polietilene
Policarbonato
Calcestruzzo
Vetro
Composito
in fibre di
carbonio
Densità
[kg/dm3]
7,9
2,7
0.9
1,2
2,5
2,3
1,6
Legno
massello
0,7
Proprietà generali: Densità
I materiali metallici hanno in genere densità elevata perché formati da elementi ad alto
numero atomico (massa maggiore) e struttura cristallina compatta (volume minore).
I materiali polimerici hanno in genere bassa densità in quanto sono costituiti
principalmente da elementi a basso numero atomico (C, H, O) con struttura solo
parzialmente ordinata (semicristallini o amorfi).
I materiali ceramici più usati come calcestruzzo e vetro hanno densità intermedie tra
metalli e polimeri
Attenzione all’unità di misura utilizzata in
questo grafico!!!
1 kg/m3 = 10-3 kg/dm3
Densità Polietilene = 0,9 kg/dm3 = 900 kg/m3
Le Proprietà Meccaniche:
rigidità
resistenza
tenacità
duttilità
durezza
Introduzione alle proprietà meccaniche dei materiali: Obiettivo
Conoscendo:
Forze agenti su un oggetto
Dimensioni dell’oggetto
Possiamo determinare:
Sforzi agenti
Deformazioni conseguenti
Questo ci permetterà di ottenere, attraverso dei risultati sperimentali, le
prime informazioni sul comportamento meccanico di un materiale e
quindi saremo in grado di selezionare i materiale più adatto a
determinate applicazioni. Esempi:
Di che materiale devo fare la mensola di una libreria di 4 mm di
spessore affinchè una volta carica di libri non si fletta eccessivamente?
Lo schienale di una sedia avente uno spessore di 3 mm può essere
realizzato in polipropilene?
Introduzione alle proprietà meccaniche dei materiali: concetto di forza
La forza è una grandezza fisica vettoriale, che si manifesta nell'interazione di due o più
corpi e che cambia lo stato di quiete o di moto dei corpi stessi.
Una grandezza vettoriale è una grandezza fisica che viene descritta dal punto di vista
matematico da un vettore, ovvero da una grandezza definita da tre parametri: il
modulo (intensità), la direzione e verso. Quando necessario, viene specificato anche il
punto di applicazione.
Al contrario le grandezze scalari sono definite solo dal modulo.
Forza :
F = m· a (dalla seconda legge di Newton)
[F] = [Kg m / s2] = [N] = Newton
Elementi di un vettore
generico
m= massa a = accelerazione
[kg]
La forza risultante è pari alla somma
vettoriale delle altre due forze (regola
del parallelogramma).
[m/s 2]
Introduzione alle proprietà meccaniche dei materiali: concetto di forza
Una forza di 1 N imprime ad un corpo con la massa di 1 kg l'accelerazione di 1 m/s².
Le forze sono quindi le cause del moto dei corpi, possono pertanto mettere in moto un
corpo che si trovava precedentemente in stato di quiete, modificare il movimento di un
corpo già precedentemente in moto, o riportare il corpo in stato di quiete.
Forza nucleare
Forza gravitazionale
Forza elettromagnetica
Forza gravitazionale e
Vincoli (riconducibili a forze
elettromagnetiche
Introduzione alle proprietà meccaniche dei materiali :
Condizioni fondamentali di carico
Una forza applicata ad un corpo è spesso indicata come carico. I solidi possono
essere sottoposti a diverse condizioni di carico. Ci sono 5 condizioni fondamentali di
carico: trazione, compressione, taglio, flessione e torsione.
Condizioni
fondamentali
di carico
Introduzione alle proprietà meccaniche dei materiali:
Condizioni fondamentali di carico
Trazione: quando un corpo è sollecitato da due forze esterne (oppure da una forza e
una reazione vincolare) di uguale intensità, aventi la stessa direzione (perpendicolare
alla sezione trasversale del corpo) ma verso opposto. In tali condizioni di carico, il
corpo tende ad allungarsi e a contrarsi trasversalmente.
Compressione è l’opposto della trazione. In tali condizioni di carico, il corpo tende ad
accorciarsi e ad allargarsi trasversalmente.
La flessione comporta l’applicazione di un carico che causa l’incurvarsi del materiale
e pone il materiale in compressione da un lato e in trazione dall’altro.
Il taglio comporta l’applicazione di un carico parallelamente ad un piano del corpo e
comporta una variazione di forma del corpo stesso: una parte del corpo slitta rispetto
all’altra.
Torsione è l’applicazione di una forza che produce una rotazione di una parte del
corpo rispetto all’altra.
Introduzione alle proprietà meccaniche dei materiali :
Il corpo è deformabile
Qualsiasi corpo soggetto a forze subisce una certa variazione delle sue dimensioni
Nella progettazione e realizzazione di oggetti e componenti è importante sapere:
sotto quali forze un oggetto si rompe (oppure si deforma in modo permanente);
oppure di quanto cambia le sue dimensioni se soggetto ad una forza non sufficiente
per romperlo (ma solo per deformarlo in modo permanente);
A tal fine occorre conoscere le dimensioni iniziali dell’oggetto e introdurre il concetto di
sforzo e deformazione.
Lo sforzo può essere valutato come il rapporto fra la forza applicata e le dimensioni
dell’oggetto; la deformazione come il rapporto fra la variazione di dimensioni e le
dimensioni iniziali dell’oggetto.
Introduzione alle proprietà meccaniche dei materiali : Sforzi
e deformazioni
Sezione
trasversale
del
campione
Introduzione alle proprietà meccaniche dei materiali :
Trazione e compressione
Lo sforzo di trazione o compressione è determinato da due forze (oppure da una
forza applicata e da una reazione vincolare) uguali ed opposte che agiscono nella
direzione perpendicolare alla superficie trasversale del corpo.
Ogni elemento rettangolare in cui si può immaginare di dividere il corpo si allunga o si
accorcia di una quantità ΔL
• Se il corpo tende ad allungarsi nella direzione della forza si parla di deformazione a trazione
• Se il corpo tende ad accorciarsi nella direzione della forza si parla di deformazione a
compressione
Introduzione alle proprietà meccaniche dei materiali : Sforzi
e deformazioni
Consideriamo una barra di sezione trasversale A0 (area della sezione trasversale in [m2])
sottoposta ad una forza di intensità F (quindi ogni sezione trasversale della barra in esame
sarà soggetta ad una forza F) perpendicolare alla sezione stessa. Si definisce sforzo di
trazione o normale (σ) il rapporto fra la forza applicata (F) e la sezione iniziale (A0).
σ = F / A0
Unità di misura (SI)
[σ] = N / m2 = Pa = Pascal
O più spesso:
[σ] = MPa = megaPascal = 106 Pa
Ipotizziamo che la barra in esame, di lunghezza iniziale l0, si deformi fino a raggiungere una
lunghezza finale pari a l, si definisce deformazione (e) il rapporto fra l’allungamento subito
(Δl = l-l0) e la lunghezza iniziale (l0).
e = (l – l0) / l0 = Δl / l0
Unità di misura:
[e] = adimensionale [m/m] o [mm/mm]
Può essere anche espressa come deformazione
percentuale: ε% = ε ·100 = (Δl / l0) ·100
Introduzione alle proprietà meccaniche dei materiali : Sforzo
di taglio
Lo sforzo di taglio (o sforzo tangenziale) è determinato da due forze (oppure da
una forza applicata e da una reazione vincolare) uguali ed opposte che agiscono
su direzioni fra loro parallele e parallele alla superficie trasversale del corpo.
Ogni elemento rettangolare in cui si può immaginare di dividere il corpo si deforma
inclinandosi di un angolo θ.
Ogni sezione trasversale del corpo sarà soggetta alla forza di taglio F.
Introduzione alle proprietà meccaniche dei materiali : Sforzi
e deformazioni
Consideriamo una barra di sezione trasversale A (area della sezione trasversale in [m2])
sottoposta ad una forza di taglio di intensità S (quindi ogni sezione trasversale della barra in
esame sarà soggetta ad una forza S) parallela alla sezione stessa. Si definisce sforzo di
taglio o tangenziale (t) il rapporto fra la forza applicata (S) e la sezione trasversale (A).
τ= S /A
Unità di misura
[τ] = N / m2 = Pascal
O più spesso:
[t] = MPa = megaPascal = 106 Pa
Uno sforzo di taglio (o sforzo tangenziale) determina una deformazione di taglio dovuta allo
spostamento delle sezioni trasversali della barra. Immaginando che lo spostamento di valore
a si verifichi fra due superfici poste a distanza h, si definisce deformazione di taglio g il
rapporto fra lo spostamento a e la distanza h, che equivale alla tangente dell’angolo di
inclinazione θ (per angoli piccoli g = q)
γ = a / h = tg θ
Unità di misura
[γ] = adimensionale [m/m] o [mm/mm]
LA PROVA DI TRAZIONE
La prova di trazione consente di determinare alcune proprietà meccaniche dei
materiali attraverso l’acquisizione della curva sforzo/deformazione di un materiale.
In questa prova un provino, di dimensioni e geometria opportuna, viene tirato fino a
rottura in un tempo relativamente breve.
Macchina di trazione
La forza (carico) applicata viene
misurata attraverso una cella di carico,
mentre la deformazione viene misurata
con un estensimetro attaccato al
campione mediante dei morsetti. I dati
vengono acquisiti da un computer e i
valori del carico vengono convertiti in
valori dello sforzo. Si costruisce quindi
la curva sforzo-deformazione.
La geometria dei provini può variare in
base al tipo di materiale da testare, dal tipo
di componente da cui è stato ricavato il
provino (lamiera, tubo, nastro) e dal tipo di
tecnologia con cui è stato prodotto
(fusione, laminazione ecc.).
Per uniformare i risultati e renderli
confrontabili si fa riferimento alla
normativa che stabilisce come deve
essere condotta la prova.
Provini metallici
La prova di trazione
Geometria dei provini
Anche i provini sono
standardizzati (geometria
e dimensioni stabilite
dalla normativa di
riferimento)
Provini in materiale
polimerico
La forma del provino è tale che la deformazione e
la rottura del provino avvengano in corrispondenza
del tratto utile. Il raccordo presente fra il tratto utile
e gli afferraggi evita che la rottura avvenga in
corrispondenza delle ganasce, dove, oltre allo
sforzo di trazione, si ha anche l’effetto della
compressione dovuta alle ganasce stesse.
PROVA DI TRAZIONE
CURVA SFORZO – DEFORMAZIONE (σ/ε)
COMPORTAMENTO MECCANICO DEL MATERIALE
COMPORTAMENTO
ELASTICO
COMPORTAMENTO
ELASTO-PLASTICO
Curva sforzo/deformazione: Il comportamento elastico
Quando un materiale presenta un comportamento elastico, lo sforzo è direttamente
proporzionale alla deformazione (quindi l’andamento σ/ε è rappresentato da un retta).
In questo caso il provino arriva a rottura senza
deformarsi in modo permanente (irreversibile), ovvero
dopo eventuale rottura o nel caso si rimuova il carico
prima di giungere a rottura, il provino ritorna alle
dimensioni iniziali.
Molti materiali a basse deformazioni (ε% generalmente
inferiori allo 0.1 %) presentano un comportamento
elastico lineare, ovvero reversibile.
Questo comportamento è dovuto ad uno spostamento
reversibile degli atomi dalla loro posizione di equilibrio.
Il comportamento elastico del materiale e quindi la proporzionalità fra sforzo e
deformazione è rappresentato dalla seguente formula:
σ=Eε
legge di Hooke
dove E è una costante di proporzionalità, chiamata modulo di elasticità o modulo di
Young ed è caratteristica per ogni materiale. Maggiore è la pendenza della curva
sforzo-deformazione, maggiore è il valore del modulo di elasticità.
Curva sforzo/deformazione: Il comportamento elasto-plastico
Nel caso di materiali a comportamento elasto-plastico, la curva sforzo-deformazione
può essere suddivisa in due zone: la prima è rappresentativa di un iniziale
comportamento elastico del materiale, la seconda di un successivo comportamento
plastico.
Nella zona a comportamento elastico il
materiale presenta il comportamento
descritto prima (legge di Hooke).
Quando lo sforzo supera il valore critico,
detto sforzo di snervamento σs (limite
elastico) inizia la zona a comportamento
elasto-plastico, ovvero il materiale non
segue più la legge di Hooke e, rimuovendo
lo sforzo applicato o se si arriva a rottura, nel
provino rimane una deformazione residua
permanente, detta deformazione plastica.
Questo comportamento è dovuto ad uno
spostamento non reversibile degli atomi
dalla loro posizione di equilibrio.
COMPORTAMENTO ELASTICO
COMPORTAMENTO ELASTO-PLASTICO
Perché alcuni materiali presentano un comportamento
elastico ed altri elasto-plastico?
Il motivo per cui alcuni materiali mostrano un comportamento elastico ed altri elastoplastico può essere ricondotto alla loro struttura, in particolare alla “stabilità” degli
atomi rispetto alla loro posizione di equilibrio. Se dopo essere stati perturbati
dall’applicazione della forza, essi tendono a tornare spontaneamente e rapidamente
alla loro posizione di equilibrio, il comportamento macroscopico del materiale sarà di
tipo elastico.
Il comportamento elastico è mostrato dai
materiali ceramici e dai vetri, che avendo
un elevato modulo di Young (E) mostrano
delle deformazioni elastiche molto
piccole, e dai polimeri elastomerici, che
avendo bassissimo modulo di Young,
sono fortemente deformabili
elasticamente.
Mostrano comportamento elasto-plastico
quasi tutti i metalli (tranne ghise e bronzi)
e molti polimeri termoplastici.
GRANDEZZE OTTENIBILI DALLE CURVE SFORZO-DEFORMAZIONE
Dalle curve sforzo e deformazione, ottenute mediante la prova di trazione, si
possono ricavare le seguenti quattro grandezze, che rappresentano quattro principali
proprietà dei materiali:
• Modulo di elasticità (E) o modulo di Young, la cui unità di misura in genere è GPa;
• Il limite elsatico o sforzo di snervamento (σS, σsn oppure σy ) (in inglese Tensile Yield
Strength TYS), in genere misurato in MPa;
• Sforzo di rottura (σR oppure R) (in inglese Ultimate Tensile Strength UTS o TS), in
genere misurato in MPa);
• allungamento percentuale a rottura εR (%) (An%, in inglese %EL) (misurato con un
estensimetro)
Materiale con COMPORTAMENTO ELASTICO (anche fragile)
Se lo sforzo applicato è inferiore a quello
di rottura (σR), il materiale opera in
campo elastico; quindi, rimuovendo lo
sforzo applicato, la deformazione viene
recuperata. Se si supera lo sforzo di
rottura, si supera la massima resistenza
meccanica del materiale e la sedia si
rompe.
Materiale con COMPORTAMENTO ELASTO-PLASTICO (duttile)
Se lo sforzo applicato è inferiore a quello
di snervamento (σS), il materiale opera
in campo elastico; quindi, rimuovendo lo
sforzo applicato, la deformazione viene
recuperata. Se lo sforzo è superiore a
quello di snervamento ma inferiore a
quello di rottura (σR), rimuovendo il
carico applicato, la sedia rimane
deformata in modo permanente, poichè
viene recuperata solo la deformazione
elastica.
Curva sforzo-deformazione per comportamento elastico lineare
Per piccole deformazioni tutti i materiali hanno un comportamento elastico lineare.
Le deformazioni sono in genere dello 0,1%.
Nel campo elastico lineare la curva a trazione e quella a compressione hanno lo
stesso modulo di Young, cioè la stessa pendenza.
L’area sottesa alla curva rappresenta l’energia elastica per unità di volume. Quando
il carico viene rimosso il provino ritorna alle dimensioni iniziali e l’energia elastica
immagazzinata durante la deformazione viene restituita integralmente.
La proporzione fra
sforzo e
deformazione è
rappresentabile con
una retta la cui
pendenza è il
modulo di Young (E)
Alcuni materiali presentano solo comportamento approssimato
a quello elastico lineare
Acciai per
molle
Allumina, vetro
Polimetilmetacrilato a bassa temperatura
Bachelite (resina fenolica)
Curva sforzo-deformazione per comportamento elastico non-lineare
Alcuni materiali presentano comportamento elastico non lineare
Gomma
Nel caso della gomma (elastomero) per piccoli
sforzi di trazione si hanno elevate
deformazioni; in genere sono dell’ordine di 5
volte la dimensione iniziale del campione.
L’area sottesa alla curva rappresenta l’enorme
quantità di energia di deformazione
immagazzinata che viene restituita
integralmente quando il carico viene rimosso.
Il comportamento a compressione è diverso
da quello a trazione.
Legno
Il legno sollecitato a trazione (nella direzione
delle fibre) si deforma poco prima di arrivare a
frattura; mentre a compressione per piccoli
sforzi si hanno elevate deformazioni, cioè si
ha un elevata deformazione nella direzione
delle fibre prima di arrivare a frattura.
Alcuni materiali presentano comportamento elastico non lineare
Calcestruzzo
500
Stress (MPa)
375
250
Ghisa
125
0
0
0.002
0.004
0.006
0.008
Strain
Gray Cast Iron
Il calcestruzzo è un materiale composito
formato dalla pasta di cemento e dagli
aggregati. Entrambi i costituenti presentano un
comportamento elastico lineare (fragile). A
trazione ha un comportamento elastico non
lineare mentre a compressione ha un
comportamento duttile, dovuto alla differente
rigidità (E) dei materiali che lo compongono.
Durante la deformazione si formano delle
microfressure che, scorrendo all’interno della
pasta di cemento, determinano la sostanziale
deviazione della curva σ/ε dalla linearità.
Superato lo sforzo massimo (resistenza del
materiale), si ha una rottura di tipo duttile.
La ghisa ha un comportamento
fragile, ma la curva σ/ε ha un
andamento elastico non lineare.
Il comportamento elasto-plastico
A sforzi maggiori di quelli compresi nel tratto elastico, in molti materiali
intervengono deformazioni non reversibili, dette deformazioni plastiche.
Il comportamento elasto-plastico
Nei materiali cristallini (materiali metallici), le deformazioni plastiche avvengono
per scorrimento di dislocazioni.
Deformabilità dei metalli: elevata
Avviene per scorrimento di dislocazioni
I metalli sono duttili
Legame non direzionale
Deformabilità dei ceramici: spesso
trascurabile.
Legame covalente: direzionale, oppone
grande resistenza allo scorrimento
Legame ionico impedimento dovuto a
repulsioni elettrostatiche fra ioni nel
corso degli scorrimenti
Deformazione irreversibile nei
polimeri: scorrimento relativo di catene
polimeriche, rotazioni di legami.
Curva sforzo-deformazione per il comportamento elasto-plastico
1-tratto elastico lineare
3-si raggiunge il limite
elastico Y
2-il tratto elastico
lineare continua
4-deformazione plastica
Curva sforzo-deformazione per il comportamento elasto-plastico
5-si raggiunge il limite di
snervamento (ε = 0,2%)
7-inizio strizione
6-si raggiunge il limite ultimo
UTS (resistenza materiale)
8-frattura
Curva sforzo/deformazione:
Grandezze ricavabili
1
96
2
3
E dal tratto 1
σs dal tratto 2
σR al punto 3
An% dal punto 4
4
Tensile test necking simulation
Intensità della
deformazione di un provino
duttile nel corso della prova
di trazione
Carico di snervamento allo 0,2% (o ingegneristico)
Il carico di snervamento σS (σsn) o TYS è una grandezza molto importante nelle
progettazione strutturale, in quanto è la sollecitazione al di sopra della quale nel
materiale (materiali metallici) si manifestano significative deformazioni plastiche.
Dato che nel diagramma σ/ε non sempre è definibile con esattezza un punto in cui
finisce il campo elastico e inizia quello plastico (ovvero l’inizio del moto delle
dislocazioni), il carico di snervamento (in questo caso carico di snervamento
ingegneristico) è definibile come la sollecitazione in corrispondenza della quale si ha
una deformazione plastica residua dello 0,2% (a volte, in dipendenza della specifica
applicazione, anche 0,1% o 0,5%).
σS
σS si determina tracciando una
retta parallela al tratto elastico
della curva σ/ε partendo da un
valore di deformazione pari allo
0,2% (cioè 0,002).
Curva sforzo-deformazione con punto di snervamento visibile
Alcuni metalli duttili, come l'acciaio dolce (a
basso tenore di carbonio), presentano un
comportamento sostanzialmente lineare fino al
raggiungimento del punto di snervamento
superiore, quindi lo sforzo σ cala bruscamente
rimanendo sostanzialmente costante (punto di
snervamento inferiore), mentre la deformazione
aumenta. Successivamente σ ritorna a
crescere. Il punto di snervamento inferiore
viene assunto come il carico di snervamento di
riferimento per la progettazione.
Il processo di snervamento è un fenomeno locale di
deformazione plastica dovuto allo scorrimento delle
dislocazioni. Le bande di scorrimento (dette bande di
Luders) si sviluppano, in genere, con un angolo di
45 rispetto all’asse del provino. Tali bande si
propagano su tutta la sezione di prova, poi lo sforzo
ricomincia a crescere a causa dell’interazione delle
dislocazioni, che ostacolandosi, portano al fenomeno
dell’incrudimento (ovvero lo sforzo necessario per
continuare la deformazione del materiale aumenta).
Determinazione della tensione di snervamento in tre casi
limite
a) Il passaggio dal comportamento elastico a quello plastico è definibile
b) Snervamento visibile (sforzo di snervamento superiore e inferiore)
c) Il passaggio dal comportamento elastico a quello plastico non è definibile
con esattezza (σS determinata allo 0.2% di deformazione)
Sforzo (carico) di rottura
Il sforzo di rottura σR, UTS o TS è il valore massimo di resistenza raggiunto nel
diagramma sforzo-deformazione. Infatti superato tale carico si manifesta sul provino
un restringimento localizzato della sezione (strizione); di conseguenza lo sforzo σ
diminuirà all’aumentare della deformazione fino al sopraggiungere della rottura, in
quanto esso è calcolato in riferimento alla sezione iniziale del provino (sforzo
nominale o ingegneristico: σn = F/A0) e non a quella effettiva. Considerando la
sezione effettiva per il calcolo dello sforzo, si osserverebbe che tale sforzo (sforzo
reale), nei materiali metallici, continua in realtà ad aumentare fino al valore in cui si
ha la rottura. Più il metallo è duttile, più sarà evidente la strizione sul provino e quindi
maggiore sarà la diminuzione dello sforzo nominale (o l’aumento di σ reale).
Curva σ/ε di un acciaio a basso
tenore di carbonio
σR,
Allungamento percentuale a rottura e strizione
percentuale
Misure della duttilità
Lo = Lunghezza del tratto utile prima della prova
Lf = lunghezza finale ottenuta ricongiungendo le due metà del provino e
misurando la lunghezza finale del tratto utile (si considera solo la deformazione
permanente)
Durante la prova di trazione si può utilizzare un estensimetro per valutare in
continuo la deformazione del provino.
La strizione percentuale si misura conoscendo il diametro iniziale della sezione
del provino e misurando il diametro della sezione di rottura (sezione minima)
PRINCIPALI PROPRIETÁ MECCANICHE RICAVABILI DALLA CURVA
SFORZO-DEFORMAZIONE
Proprietà meccanica
Grandezza caratteristica
Unità di misura
Rigidezza
Modulo di elasticità (E)
GPa
Resistenza
Sforzo di snervamento σS e
sforzo di rottura σR
MPa
Duttilità
Allungamento a rottura An%
Strizione percentuale z%
%
Tenacità
•Modulo di elasticità
•Sforzo di snervamento
•Deformazione a rottura
PROPRIETÁ MECCANICHE: RIGIDEZZA
La rigidezza di un materiale è correlata alla sua capacità di subire deformazioni in
campo elastico. La grandezza caratteristica che ci permette di definire la rigidezza
di un materiale è il modulo di elasticità (E) (o modulo elastico).
Dalla pendenza del tratto elastico delle 3 curve
sforzo-deformazione si deduce che il materiale
3 ha una rigidezza maggiore del materiale 1;
infatti la pendenza della curva aumenta dal
materiale 1 al materiale 3 e quindi aumenta il
relativo modulo di elasticità.
Un materiale con basso modulo di elasticità
(e quindi bassa rigidezza) viene definito
cedevole oppure flessibile.
Possiamo dire che a un’elevata energia di
legame corrisponde un maggior valore del
Modulo Elastico (E) e quindi una maggior
rigidezza; infatti serve una maggior energia
per spostare gli atomi dalla loro posizione di
equilibrio (ovvero per deformare
elasticamente il materiale).
E
Il modulo di Elasticità (Rigidezza) dei materiali
Valori di rigidezza (E) per alcuni materiali:
Acciaio: 200 GPa
Alluminio: 74 GPa
Rame: 125 GPa
Polietilene: 0,8 GPa
Calcestruzzo: 20 GPa
Vetro: 70 GPa
Composito a fibre di vetro: 22 GPa
Composito a fibre di carbonio: 110 GPa
Legno massello: 15 GPa
Gomma naturale: 0,002 GPa
La rigidezza è la caratteristica meccanica più importante dei compositi a fibre
di carbonio, in quanto associano tale proprietà ad una notevole leggerezza
(applicazione: telaio automobili Formula 1)
PROPRIETÁ MECCANICHE: RESISTENZA
La resistenza di un materiale è correlata alla sua capacità di sopportare delle
forze applicate senza rompersi e senza deformarsi in modo permanente. La
grandezza caratteristica che ci permette di definire la resistenza di un materiale
dipende dal tipo di materiale, ovvero se tale materiale si comporta in modo elastoplastico oppure elastico:
comportamento elasto-plastico → sforzo di snervamento σS
comportamento elastico (materiali fragili) → sforzo di rottura σR
σS
σR
In entrambi i casi la resistenza
aumenta passando dal
materiale 1 al materiale 3.
In questo esempio la rigidezza
(E) e la duttilità (εR) dei tre
materiali sono molto simili.
In genere un materiale poco resistente viene definito tenero.
La resistenza dei materiali
ATTENZIONE: Per ceramici e
vetro le resistenze riportate
sono a compressione
PROPRIETÁ MECCANICHE: DEFORMABILITÁ PLASTICA (DUTTILITÁ)
La deformabilità plastica di un materiale è correlata alla sua capacità di sopportare
grandi deformazioni plastiche senza rompersi. Tale caratteristica, soprattutto per i
materiali metallici, è importante, non tanto in fase di utilizzo del materiale, quanto in
fase di lavorazione. Infatti tramite deformazione plastica (es: laminazione a caldo o
a freddo, estrusione e forgiatura) è possibile produrre lamiere, barre e pezzi
forgiati. I materiali fragili, come ceramici e metalli con bassissima duttilità (bronzo e
ghisa) non sono lavorabili per deformazione plastica, pertanto vengono prodotti per
sinterizzazione (ceramici) e per colata direttamente nello stampo (ghisa, bronzo).
La grandezza a cui si fa riferimento per la
deformazione a rottura è l’allungamento percentuale
εR (An%). Nella figura vediamo che dal materiale 1 al
materiale 3 la deformazione a rottura aumenta. La
rigidezza e la resistenza in questo caso ideale sono
molto simili.
εR
La duttilità dei materiali
Perché, dopo un urto, il bicchiere si rompe e invece la
carrozzeria si deforma?
Perché il metallo di cui è costituita la carrozzeria è in grado
di assorbire una grande quantità di energia per
deformazione plastica. E’ un materiale tenace. Assorbe
dunque l’energia dell’urto senza arrivare a rottura. Il vetro
pur deformandosi fino a rottura assorbe una piccola quantità
di energia. E’ un materiale fragile.
PROPRIETÁ MECCANICHE: TENACITÁ
La tenacità di un materiale è sostanzialmente legata alla sua capacità di resistere agli
urti, ovvero la capacità di dissipare al suo interno l’energia di deformazione che può
provenire da un urto.
Un materiale a comportamento tenace si rompe in modo controllato, modificando
gradualmente la sua forma e la sua microstruttura, assorbendo, quindi, elevate
energie di deformazione. Un materiale a comportamento fragile si rompe
all’improvviso (di schianto) senza dar luogo a deformazioni permanenti di grande
entità e quindi con basse energie di deformazione.
La tenacità può essere valutata
dalla curva sforzo-deformazione
calcolando IT come il prodotto fra la
tensione di rottura e il valore
dell’allungamento a rottura. In
pratica questo è un indice della
capacità del materiale di
immagazzinare energia nel campo
elasto-plastico senza arrivare a
rottura.
Alcune curve sforzo deformazione di importanti materiali strutturali
Alcune curve sforzo deformazione di importanti materiali strutturali
Materiali tenaci o meno presentano diversi comportamenti alla frattura.
LA FRATTURA DUTTILE O FRAGILE
Duttile
Deformazione
Fragile
elevata
piccola
Bassa, si propaga al
crescere dello sforzo
elevata
Maggior parte dei
metalli, polimeri
termoplastici (sopra Tg)
Ceramici, vetri, polimeri
termoplastici (sotto Tg) o
termoindurenti
Deformazione
permanente
nessuno
Energia assorbita alla
frattura
elevata
piccola
Superficie di frattura
rugosa
lucida
sì
no
Velocità di propagazione
Tipo di materiali
Segni premonitori
Strizione
La frattura duttile
La frattura duttile avviene dopo una notevole deformazione plastica con strizione.
Frattura duttile nei metalli (coppa-cono)
Si possono individuare diversi stadi:
(1) Strizione iniziale
(2) Si formano dei microvuoti all’interno
della zona soggetta a strizione
(3) I microvuoti coalescono formando
una cricca nel centro del provino
(4) La cricca propaga verso la superficie
in direzione perpendicolare allo
sforzo applicato
(5) Quando la cricca raggiunge la
superficie la sua direzione si inclina di
45 rispetto alla direzione di trazione
e si verifica una rottura di tipo coppacono
Le fratture duttili sono meno frequenti di quelle fragili e sono principalmente causate
dal sovraccarico del componente
La frattura fragile o semifragile di un metallo
La frattura fragile o semifragile avviene con una deformazione plastica nulla o piccola
e il provino non presenta strizione.
Nei metalli la frattura fragile può essere
di due tipi:
transgranulare, quando le cricche si
propagano attraverso i grani
intergranulare, quando le cricche si
propagano seguendo i bordi dei grani.
Di solito la frattura fragile di tipo
transgranulare avanza lungo piani
cristallografici caratteristici detti
piani di clivaggio
Meccanismo di frattura fragile o duttile
Meccanismo di frattura
fragile di una lega di
magnesio AM60B, sono
indicate le facce di clivaggio.
Meccanismo di frattura duttile
di una lega di magnesio
AM60B, sono indicati i
microvuoti
Fratture duttili
Duralluminio
Cono
Coppa
Alluminio
puro
Frattura duttile
Rame
Cono
Coppa
Frattura fragile
Acciaio dolce a bassa
temperatura
Morfologie tipiche di fratture fragili al microscopio elettronico