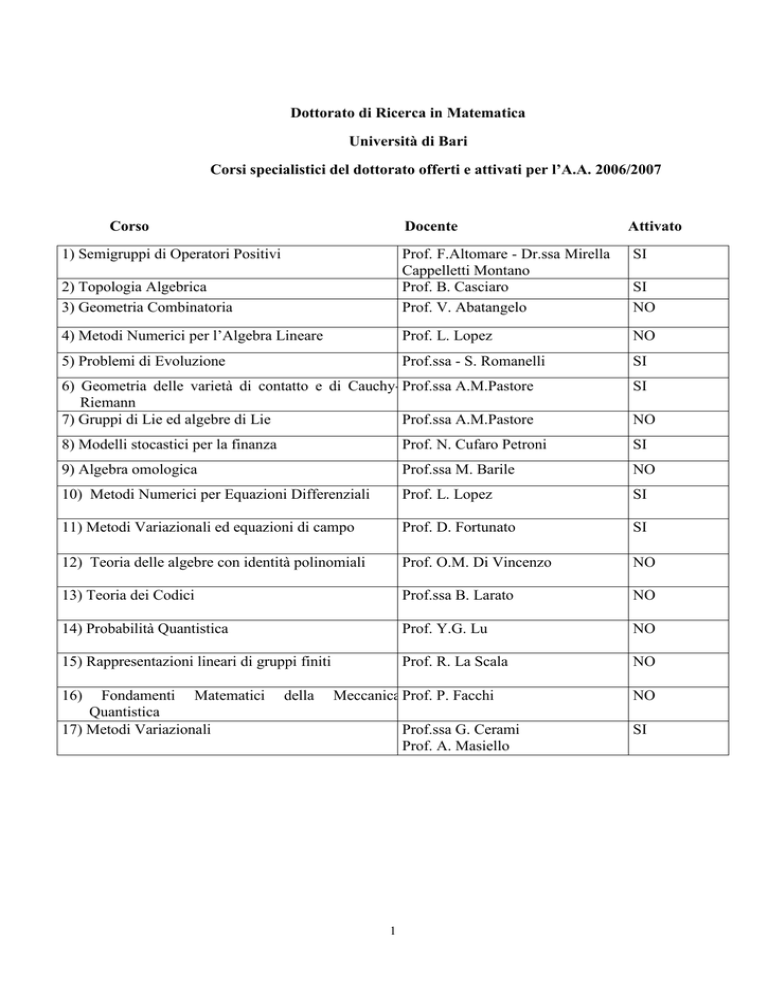
Dottorato di Ricerca in Matematica
Università di Bari
Corsi specialistici del dottorato offerti e attivati per l’A.A. 2006/2007
Corso
Docente
1) Semigruppi di Operatori Positivi
Attivato
SI
2) Topologia Algebrica
3) Geometria Combinatoria
Prof. F.Altomare - Dr.ssa Mirella
Cappelletti Montano
Prof. B. Casciaro
Prof. V. Abatangelo
4) Metodi Numerici per l’Algebra Lineare
Prof. L. Lopez
NO
5) Problemi di Evoluzione
Prof.ssa - S. Romanelli
SI
SI
NO
6) Geometria delle varietà di contatto e di Cauchy- Prof.ssa A.M.Pastore
Riemann
7) Gruppi di Lie ed algebre di Lie
Prof.ssa A.M.Pastore
SI
8) Modelli stocastici per la finanza
Prof. N. Cufaro Petroni
SI
9) Algebra omologica
Prof.ssa M. Barile
NO
10) Metodi Numerici per Equazioni Differenziali
Prof. L. Lopez
SI
11) Metodi Variazionali ed equazioni di campo
Prof. D. Fortunato
SI
12) Teoria delle algebre con identità polinomiali
Prof. O.M. Di Vincenzo
NO
13) Teoria dei Codici
Prof.ssa B. Larato
NO
14) Probabilità Quantistica
Prof. Y.G. Lu
NO
15) Rappresentazioni lineari di gruppi finiti
Prof. R. La Scala
NO
16)
Fondamenti Matematici
Quantistica
17) Metodi Variazionali
della
Meccanica Prof. P. Facchi
Prof.ssa G. Cerami
Prof. A. Masiello
1
NO
NO
SI
Corsi specialistici del Dottorato
seguiti presso altre sedi universitarie italiane o estere nell’ a.a. 2006/07
1) Introduzione alla modellazione 3D
Prof. G.Casciola - Univ. Padova
2) Analisi di superficie discrete
3) Analisi Numerica (Corso Estivo Perugia)
Prof.ssa S. Biasotti, Dr. G.Patanè
IMATI CNR Genova
Prof. C. Lubich – SMI Perugia
4) Analisi Funzionale (Corso Estivo Perugia)
Prof. E.T. Sawyer – SMI Perugia
5) Global Optimization Course
Prof. J.Pinter – Univ. Gyor Ungheria
6) Robust Optimization Summer School
7) Computational Complexity and Applications
Prof. A. Ben-Tal, Prof. M.Sim
Cortina
Combstru School - Bertinoro
8) Jump processes and finance
Prof. J.Jacod – Univ. Firenze
9) Varietà iperboliche
10) Partial Differential Equations (Corso Estivo
Cortona)
11) Teoria dei punti critici (Minicorso)
Prof. S. Trapani – Univ. Roma tor
Vergata
Prof.C.Da Fermos,Prof. P.D’Ancona
– SMI Perugia
Dott. D. Ruiz – SISSA Trieste
12) Calcolo delle variazioni (Minicorso)
Dott. M. Morini – SISSA Trieste
13) Classical and hard implicit functions theorems
Prof. M. Berti – Univ. Napoli
Dott. G. Panati – Univ. Roma La
Sapienza
15) The Mathematics of the Scrodinger Equation and Prof. K. Yajima – Univ. Tokyo
of Scattering theory in quantum mechanics
16) Stochastic programming: theory and applications Prof. S. A. Zenios, Prof. G.Pflug
Sprin School
Univ. Bergamo
17) Introduzione alla teoria analitica dei numeri
Prof. A.Zaccagnini – Univ. Parma
14) Introduction to quantum dynamics
18) Algebra combinatoria
Prof.ssa M. Bianchi – Univ. Milano
19) Teoria dei numeri
Prof. A. Mori – Univ. Torino
2
AVVERTENZE
Nell’arco dei primi due anni gli allievi devono seguire non meno di cinque corsi specialistici
(ovvero cinque moduli specialistici) offerti dal Dottorato di Ricerche di Matematica di Bari o
da altre strutture Universitarie e di Ricerca.
Di questi cinque corsi specialistici, tre devono essere scelti fra i corsi pertinenti il curriculum
nell’ambito del quale si svolgeranno le ricerche relative alla tesi di dottorato.
Almeno uno dei due corsi specialistici rimanenti deve essere pertinente a curriculum diverso dal
curriculum prescelto per la tesi di dottorato.
Almeno due di questi cinque corsi specialistici devono essere seguiti durante il primo anno.
3












